はじめに
アドベントカレンダー25日目を担当します大津です。今回のテーマは白色矮星の最大質量です。みなさん白色矮星をご存知でしょうか?代表的なものはここから約8.6光年先にあるシリウスBです。白色矮星とは恒星が長い時間光輝いた後に残った中心核であり、強い重力を持つ白色矮星は電子の縮退圧によって支えられています。

シリウスBは矢印の先。隣の明るいほうはシリウスA。シリウスは冬の大三角形をなす一角です。この画像はハッブル宇宙望遠鏡で撮影されています。
そしてこの白色矮星は限界質量が存在します。この質量をチャンドラセカール限界と呼びます。今回はその最大質量を統計力学を用いて導出してみようと思います。
(チャンドラセカールは白色矮星の最大質量が存在することを発見し、1983年にノーベル物理学賞を受賞しています。)
フェルミ統計と縮退圧
同種の多数の粒子から成る系をグランドカノニカル分布で考えます。1粒子の状態を$j$、エネルギーを$\epsilon_j$で表し、状態$j$にある粒子数を$n_j$で表します。グランドカノニカル分布の分配関数は次のようになります。
$$\Xi=\prod_{j} \Biggl( \sum_{n_j} e^{-\beta(\epsilon_j-\mu)n_j} \Biggl)$$
また$n_j$の平均値は以下のようになります。
\displaylines{
\langle n_j \rangle=\frac{1}{\beta}\frac{\partial}{\partial \mu}\text{log}\Xi_j
}
フェルミ粒子の場合、パウリの排他原理より1状態に0または1個しか存在できません。よって$n_j=0,1$となるので
\displaylines{
\Xi=\prod_{j} \Biggl( 1+e^{-\beta(\epsilon_j-\mu)} \Biggl)\\
\langle n_j \rangle =\frac{e^{-\beta(\epsilon_j-\mu)}}{1+e^{-\beta(\epsilon_j -\mu)}}=\frac{1}{e^{\beta(\epsilon_j -\mu)}+1}
}
この分布に従う粒子をフェルミ粒子といい、電子、陽子、中性子などが含まれます。粒子のエネルギーを$\epsilon$とすると、フェルミ粒子のエネルギー分布は以下のようになります。
$$dN=\frac{D(\epsilon)d\epsilon}{e^{\beta(\epsilon-\mu)}+1}$$
$D(\epsilon)d\epsilon$はエネルギーが$\epsilon$から$\epsilon+d\epsilon$までの状態数を表す状態密度です。ここで電子等のスピン1/2の粒子を扱います。スピン1/2の粒子にはスピン縮退度2(=2・1/2+1)があることに注意すると
$$D(\epsilon)d\epsilon=\frac{2}{h^3}\int d^3\boldsymbol{r}\int d^3\boldsymbol{p}=\frac{8\pi V}{h^3}p^2dp$$
今回粒子の速さが光速に近い状況を考えると$\epsilon=cp$より
$$D(\epsilon)d\epsilon=\frac{8\pi V}{h^3c^3}\epsilon^2 d\epsilon$$
と表すことができます。
また$T=0$ではフェルミ分布はある高さよりも低いエネルギー準位がすべて粒子によって占有される階段状の関数になります。これはパウリの原理より粒子系全体のエネルギーが最も低い状態だけ実現されるからである。
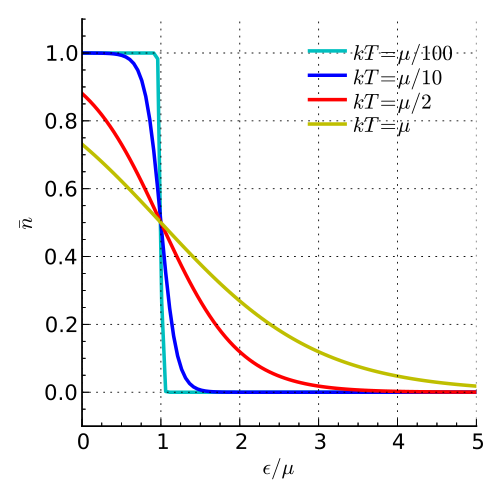
今1状態に1粒子があるので粒子のエネルギー最大値を$\epsilon_F$とおくと、粒子数は以下のようになる。
$$N=\int_0^{\epsilon_F}D(\epsilon)d\epsilon=\frac{8\pi V}{3h^3c^3}\epsilon_F^3$$
$\epsilon_F$をフェルミエネルギーと呼びます。また$\epsilon_F=cp_F$と置くことでフェルミ運動量$p_F$を定義します。
ゆえに数密度$n=\frac{N}{V}$と$p_F$で以下の関係式が導けます。
$$p_F=\hbar(3\pi^2 n)^\frac{1}{3}$$
状態密度はこの関係式を用いて以下のようにも表せます。
$$D(\epsilon)d\epsilon=\frac{8\pi V}{3h^3c^3}\epsilon^2 d\epsilon=\frac{3N}{\epsilon_F^3}\epsilon^2d\epsilon=3N\frac{p^2}{p_F^3}dp$$
よって$T=0$での1粒子あたりのエネルギーは
$$\frac{E}{N}=\int_0^{p_F}cp \cdot 3N\frac{p^2}{p_F^3}dp=\frac{3}{4}cp_F=\frac{3}{4}\hbar c(3\pi^2 n)^\frac{1}{3} $$
熱力学の関係式より$T=0$のときの圧力$P$は以下のように求まります。
\displaylines{
\biggl(\frac{\partial E}{\partial V}\biggl)_{N,T}=T\biggl(\frac{\partial S}{\partial V}\biggl) _{N,T} -P =-P\\
P=-\biggl(\frac{\partial E}{\partial V}\biggl)_N=\frac{\hbar c}{4}(3\pi^2)^\frac{1}{3}\biggl(\frac{N}{V}\biggl)^\frac{4}{3}
}
この圧力をフェルミ縮退圧と呼びます。
静水圧平衡
白色矮星はこのフェルミ縮退圧によって支えられている天体なので、次は圧力と重力の関係式を導出してみましょう。
半径$R$の球対称な天体内の重力による圧力を$P(r)$、中心から$r$内の質量を$M(r)$、天体の密度を$\rho$とします。静止した流体において重力を含めたオイラーの運動方程式は
\displaylines{
0=-\frac{1}{\rho}gradP(r)-G\frac{M(r)}{r^2}\frac{\boldsymbol{r}}{r}\\
\frac{\mathrm{d}P(r)}{\mathrm{d}r}=-G\frac{M(r)\rho}{r^2}
}
このように流体に働く重力と圧力勾配が釣り合ってる状態を静水圧平衡といいます。また$\rho$が一定と仮定すると
$$M(r)=\int_{0}^{r}4\pi^2 r^2\rho dr=\frac{4\pi}{3}\rho r^3$$
と表すことができるので、
$$\frac{\mathrm{d}P(r)}{\mathrm{d}r}=-G\frac{4\pi}{3}\rho^2 r$$
と書き表せます。圧力最大になるのは中心なので中心の圧力を$P_0$とすると
$$P_0=\int_{0}^{P_0}dP=\int_{R}^{0}\frac{\mathrm{d}P(r)}{\mathrm{d}r}dr=\int_{0}^{R}G\frac{4\pi}{3}\rho^2 r=\frac{2\pi}{3}G\rho^2 R^2$$
よって最大圧力を電子の縮退圧で支える条件は以下のようなります。
$$P_0=\frac{2\pi}{3}G\rho^2 R^2 \le\frac{\hbar c}{4}(3\pi^2)^\frac{1}{3}n^\frac{4}{3}$$
チャンドラセカール限界
天体が電子と電子1個あたり$\mu_e$個の核子(質量$m_u$)からなるとします。電子の質量は核子に比べて十分小さいので電子の質量を無視すると、$\rho=\mu_e m_u n$と表せます。これをさっきの不等式に入れて整理すると以下のようになります。
$$R^2 \le\frac{3^\frac{4}{3}\hbar c\pi^{-\frac{1}{3}}n^{-\frac{2}{3}}}{2^3G\mu_e^2m_u^2}$$
この最大半径を用いると白色矮星の最大質量は
$$M_{\text{max}}=\frac{4}{3}\pi R^3\rho=\frac{3\pi^\frac{1}{2}}{2\frac{5}{2}\mu_e^2 m_u^2}\biggl(\frac{\hbar c}{G}\biggl)^\frac{3}{2}$$
実際に$\mu_e=2$として値を代入すると$$M_{\text{max}} \sim 0.44 M_\odot$$となりました。 $M_\odot$は太陽質量を表しています。精密に計算すると$1.46M_\odot$となるようです。
終わりに
今回の計算で数値の差が生じた理由は、天体の密度を一定にしてしまったからです。本来は状態方程式を用いて厳密に求める必要があります。また別の解き方として内部エネルギーと重力エネルギーを用いたやり方もあるようです。中性子星も同じような計算で最大質量を求めることができます。(中性子星の最大質量をトルマン・オッペンハイマー・ヴォルコフ限界というようです)
シリウスBを肉眼で見られる人類は少ないと思いますが、ぜひみなさん冬の夜空を楽しんでください。
参考文献
1.青木健一郎「コア・テキスト 波・熱力学・統計力学とその応用」.サイエンス社(2025)
2.久保亮五「新装版 統計力学」,共立出版株式会社(2003)
3.巽友正「流体力学」,培風館(1982)
4.鶴剛「6章縮退したフェルミ気体とコンパクト星」,宇宙線研究室,
https://www-cr.scphys.kyoto-u.ac.jp/member/tsuru/data/lecture/AstrophysIntro2017_pdf/Section6_v2.pdf