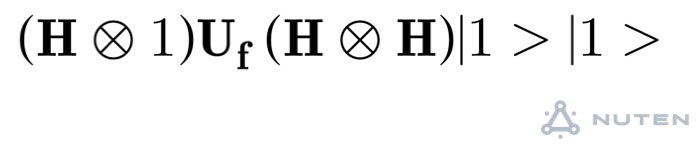
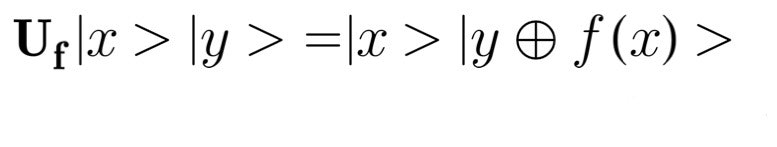#こんな人に役立つと思いまして
- 量子コンピュータやりたいけどよくわからん
- 知的好奇心で量子コンピュータ知りたい
- 基礎からだれかまとめてくれ
ちなみにこの記事は量子コンピュータで有名なドイチュの問題その2になります。その1を読んでからの方がわかるかもしれません。その1はこちら。
#ドイチュの問題復習
√2と√3それぞれを2進数展開した場合の1兆桁目が同じか否かを比較したい。f(x)={√(x+1)の1兆桁目}を計算する回路を実装しているとします。この回路を何回動かすと、一致しているかもとめられるでしょう?
###普通のコンピュータを使う場合
x=0とx=1をそれぞれ計算させて、そのアウトプットが一致するか比較します。つまり2回動かします。
###量子コンピュータを使う場合
1回の計算で終わります。それは次のように考えた場合です。
演算子Ufを以下の式のように定義します。この演算子で実効的な部分のf(x)の値は付加的なビットを用いて計算されるものとします。
このUfと用意した|1>|1>という2ビットを用いて次のようなを計算します。
Hはアダマール演算子と呼ばれる有名な演算子です。上記の演算をした結果、もしf(0)=f(1)であれば、1ビット目の状態は|1>となり、f(0)≠f(1)であれば、|0>となります。1ビット目の様子を見るだけでわかります。肝はアダマール変換で状態の和を作り出すところです。これにより、ある意味並列的に評価できるのです。f(x)の計算は1回しか行っていないため、直感的には1回の計算で答えが出たように見えます。
ですが果たしてそうでしょうか?
#付加的なビットの部分を詳しく考えてみよう
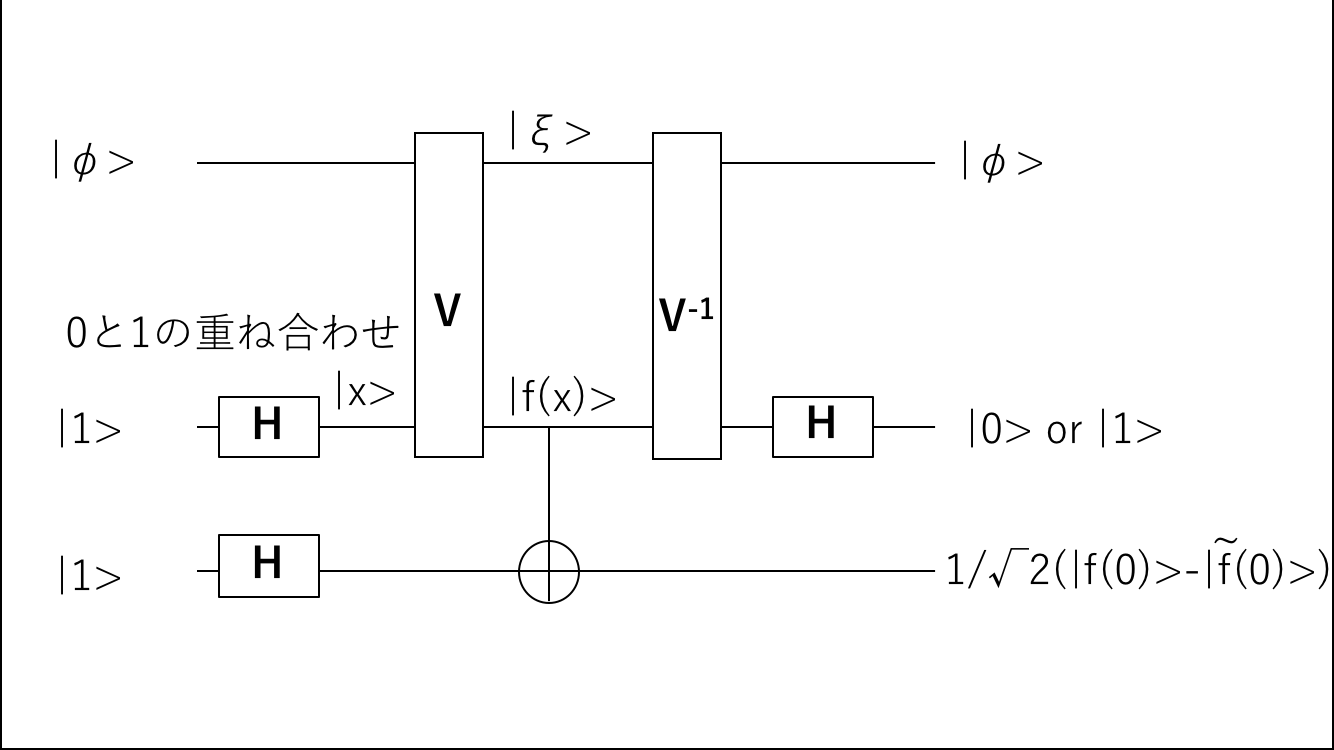
上記の議論で唯一曖昧な箇所があるとすれば、関数f(x)を計算するプロセスです。いきなりですが、付加的なビットとの相互作用を含めて、ドイチュの問題を解くアルゴリズムをグラフで書き下しましょう。
まず、入力として、|1>|1>以外にf(x)の値を計算するための付加的なr個のQビット|ξ>を考えています。rの数はf(x)を計算するための難易度によって変わります。例えば1億桁目の値を計算するのと、1兆桁目を計算するのでは、後者のほうがrは大きくなるでしょう。
|y+f(x)>を2ビット目に実現するためには、2つのステップが必要になります。
- 1ビット目を付加的なQビットととまとめて演算させて|f(x)>にする
- |f(x)>を制御ビット、2ビット目を標的ビットとしてcNOT演算を行う
1ビット目と付加的なビット全体に作用するユニタリー演算子Vで1ビット目を|f(x)>に変換します。このVの具体的な形を書き下すことはご勘弁を。ただし、量子コンピュータでもトフォリゲートと呼ばれるものを構成することができ、これを用いて任意の代数的計算が可能なため、理論上実行できるでしょう。
議論すべきは、1ビット目にはVの前にアダマール演算子を作用させているので1ビット目は状態の和になっていることです。r個の付加的なビットと1ビット目は、Vの作用で変なもつれが起こらないようにしなければなりません。すなわち、r個のQビットをまとめて|φ>として、アダマール演算子作用したあとの1ビット目を1/√2(|0>-|1>)とすると状態は1/√2|φ>|0>-1/√2|φ>|1>となり、これにVを作用させると1/√2|ξ>|f(0)>-1/√2|ξ>|f(1)>のようにr個のQビットは状態が変わったとしても、それだけで完結し、係数を変えない必要があります。
そして、1ビット目を用いて2ビット目をcNOT演算子でフリップさせます。本来その後に1ビット目に再度アダマール変換を作用させて、1ビット目が0か1かでf(0)=f(1)か否かを判定するのですが、1ビット目は|f(x)>に変換されたままです。元に戻さなければなりません。これには再度r個のQビットとの間で、Vの逆演算を作用させる必要があります。Vはユニタリー演算子で、V^-1=**V^+**のため、共役な演算子を作用させても良いです。その結果、1ビット目が|x>に戻り、アダマール演算子を作用させて、1ビット目を観測することでf(0)=f(1)かを判別します。
さて、r個のQビットを用いて|f(x)>を計算する際にVを作用させました。これが実質1回目の時間がかかる演算です。さらに1ビット目を元に戻すために、V^-1も作用させました。ここにもVの処理と同じ程度の計算時間がかかると推定されます。つまり、f(x)を計算する箇所を2回呼び出しているのです。
#これはドイチュの問題固有の話なのか?
この2回呼び出しは、ドイチュの問題のみの固有の話でしょうか。答えは否です。ただし多くの場合、計算速度向上が2倍どころではないため、量子コンピュータは意味のあるものになるのです。
#まとめ
- ドイチュの問題で1ビット目を|f(x)>とするために付加的なQビットとの間で計算をする
- ここに時間がかかる
- この|f(x)>を2ビット目とcNOT演算して計算する
- ただしこの後1ビット目は元に戻さないといけない
- これはf(x)の計算の逆演算でここでも時間がかかる
- 本来ドイチュの問題は計算が普通の半分で済むはずだがこれでは普通のコンピュータと一緒
- この理屈は別の問題でも言えることだが、別の問題では速度アップが2倍どころではないため意味が出てくる
次は有名なベルシュタインとバジラ二の問題を説明します。
こちらも参考にどうぞ
量子コンピュータのための量子論