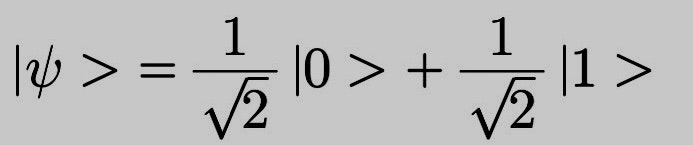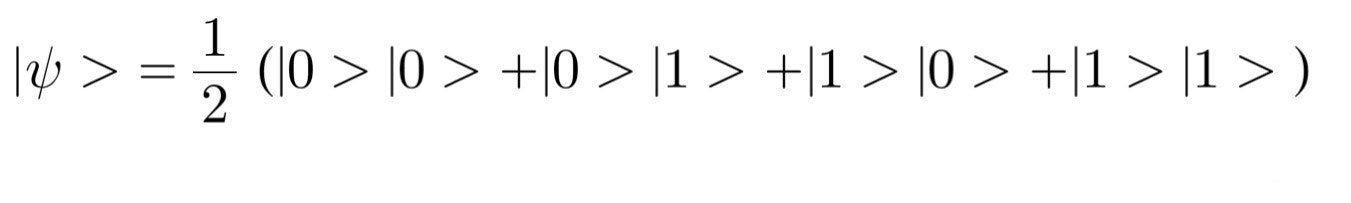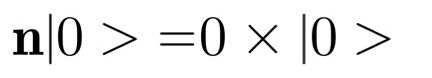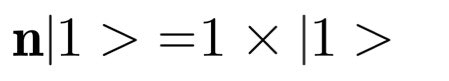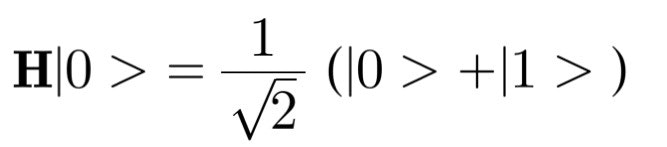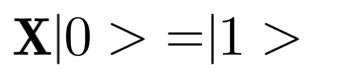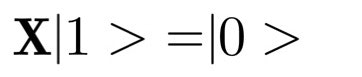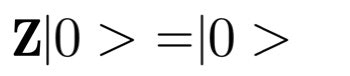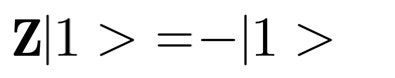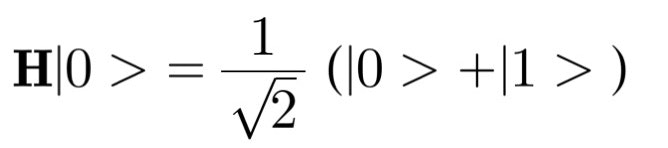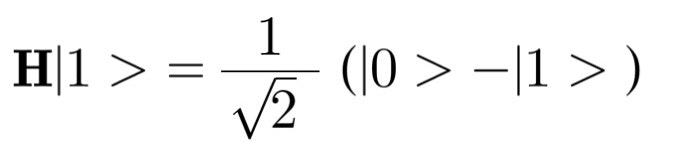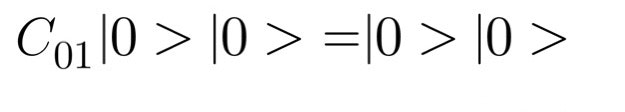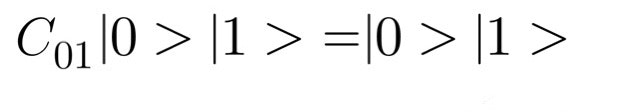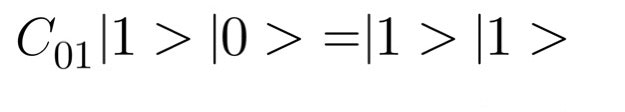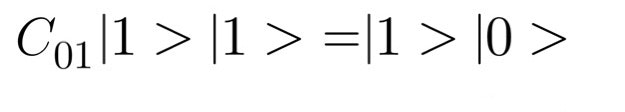こんな人に役立つと思いまして…
- 量子コンピュータやりたい、でも量子論なんて知らん
- 量子力学とか難しいから何言ってるか分からん
- 細かいことはいいから量子コンピュータ理解するための最小限の量子論の知識が欲しい
以下、自分の中のまとめも兼ねているため悪しからず。多分何回かに分けて記事にすると思います。
量子コンピュータの超簡単な基本事項
ざっくり言うと量子コンピュータは量子という「粒子のようなもの」をビットにしたコンピュータのことです。量子コンピュータにはゲート式とイジング式があり、ゲート式は0と1の状態をビットとして扱うので今のコンピュータに近く、とっかかりやすいです。量子コンピュータとして将来どちらの方式がマウントを取っているかわからんですが、ここではゲート式に絞って話を進めます。
今のコンピュータと量子コンピュータには根本的な違いがあり、それはビットに「量子」を使うということです。普通のビットは0か1のどちらかの状態しかとれないですが、量子はビットが0という状態と1という状態の「和」を作ることができます。「状態の和」とは一回の測定に対して確率的に、0の状態が観測できたり、1の状態が観測できたりする特殊な状態のことです。これは電圧がしきい値より高いか低いかで0と1を設定し計算を行う今のコンピュータでは考えていない事象です。量子の状態の和は後述する演算子に相当する操作で人為的にコントロールできます。どちらの状態が出てくるかは測定するまでわかりません。この状態の和を活用して、通常より少ない計算回数で結果を得られるのが量子コンピュータです。
状態の書き方
ほかの学問ではあまり見ない特殊な記法を、慣用的に、量子論では用いています。量子論でxという状態は|x>という記号で表します。例えばビットが0という状態は|0>と表します。0と1の状態の和は下記のように表すことになります。
それぞれの係数の2乗がその状態をとる確率を意味します。この場合は0を1/2の確率で、1を
1/2の確率でとることを表しています。
ビットが2つある場合、つまり量子が2つある場合ですが、以下のように表します。
|x>|y>という記述に対して|x>は一つ目のビット、|y>は二つ目のビットを表します。係数の2乗がその状態の確率を表すことは同じです。例えば|0>|1>に着目すると1ビット目が0、2ビット目が1である状態でそれを観測できる確率が1/4であるということを意味しています。
演算子を作用させるとは?
量子論を始めて最初に突き当たる難題が、状態に演算子を作用させるとはどういう意味?ということでしょう。
一般に演算子を状態に作用させると、その状態を変化させます。例えば|0>という状態に演算子Xを作用させると|1>になるといった具合です。
状態を定数倍する演算子も存在します。例えばnという演算子を下記のルールに基づくように状態を定数倍する演算子と定義することもできます。
また和の状態を作る下記演算子も定義することができます。
量子コンピュータでの代表的な演算子を以下に説明します。
代表的な演算子
フリップ演算子 X
0の状態を1の状態に、1の状態を0の状態に反転させる演算子です。
位相反転演算子 Z
下記のような演算をするものです。なぜこれを位相反転と言うかはブロッホ球というものの考え方を導入する必要があるので、ここではふーんくらいにしたください。
ブロッホ球参考
Wikipedia
アダマール演算子 H
状態和を作る演算子です。これは1/√2(X+Z)という演算子と同じです。状態の和を作ることができます。
cNOT演算子 C01
二つのビットに対して働く演算子も考えられます。この演算子は1ビット目が0だった場合には2ビット目に対して何もせず、1ビット目が1だった場合には2ビット目を反転させます。ちなみに添字の0は1ビット目を表し添字の1は2ビット目を表します。Pythonのリストのindexが0の時に一つ目の値を指定するするのと同じ考え方です。
まとめ
- 今のコンピュータは電圧高い=「1という状態」、電圧低い=「0という状態」に割りつけその2パターンしかないが、量子力学では「0という状態と1という状態の和」という概念を使える。
- そのかわりビットは電圧ではなくスピンと呼ばれる量だったり離散化したエネルギーだったりする。
- 状態は量子論特有の|x>という記号で表す。これはビットがxという状態という意味である。(x=0 or 1)
- 状態は演算子を作用させることで変えることができる。演算子に相当する機器は量子コンピュータに実装することができる。
以上が、ゲート式の量子コンピュータを理解する上で、最低限、知っておけば良い全てのことです。次回は量子コンピュータ最初のアルゴリズムであるドイチュのアルゴリズムについて触れます。