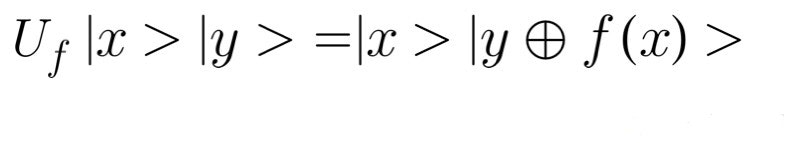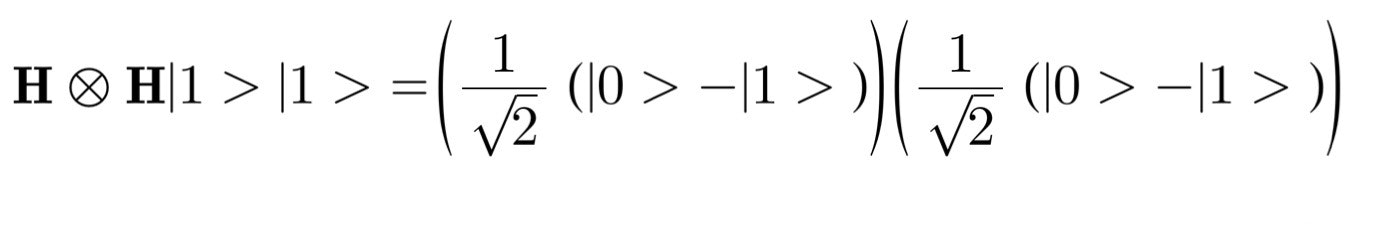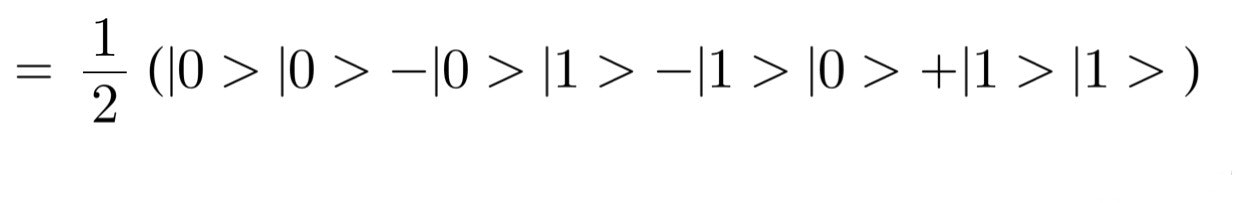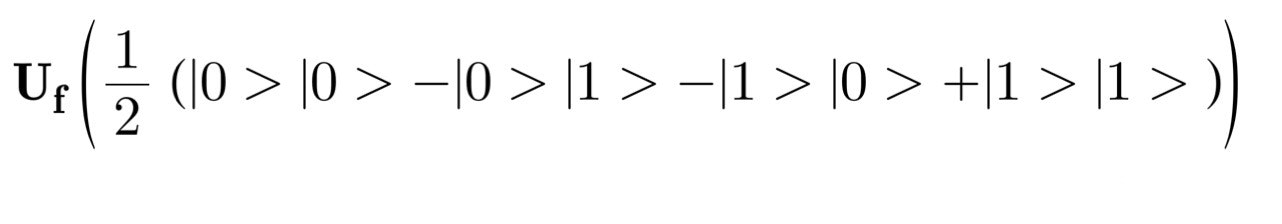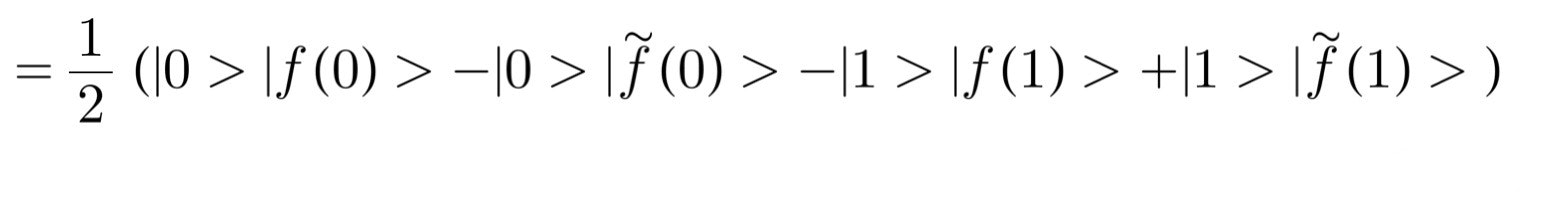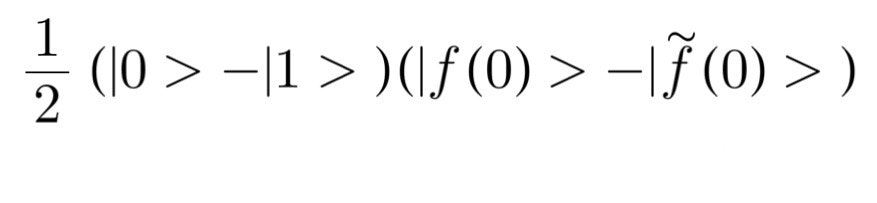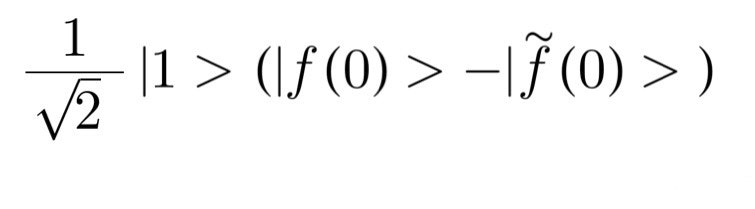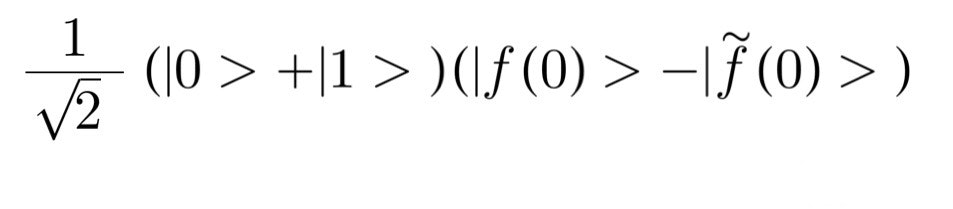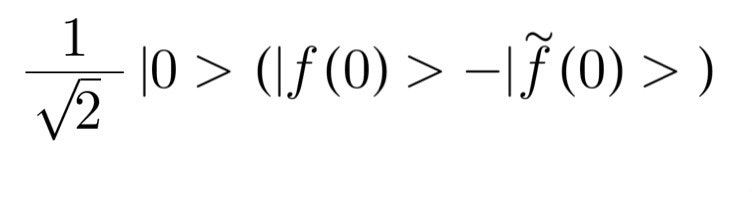こんな人に役立つと思いまして
- 量子コンピュータ始めてみたいけど量子論とかわからん
- 量子コンピュータで考えられてるアルゴリズムって何があるの?
- だれか量子コンピュータのまとめプリーズ
自分の覚えとしても書いています悪しからず。こちらを先に読んどくとたぶんわかりやすいです。
ドイチュの問題って?
もっとも初期に、量子コンピュータが実現できると役にたつんじゃね?と人々に思わせるきっかけとなったアルゴリズムです。
思考実験をしましょう。√nを2進数の小数で書きます。その小数点以下1兆桁目の数字が0か1かを計算するコンピュータがあるとします。あなたは√2と√3の1兆桁目の数字が一致するか調べたいです。何回このコンピュータに計算させれば調べられるでしょう?
普通のコンピュータを使う場合
エクセルで√2の2進数展開を計算させ、1兆桁目をメモります。次に√3の2進数展開を計算させ1兆桁目をメモります。(実際にはエクセルでは1兆桁目まで出力させられないですがイメージの話)そして1兆桁目を比較すると同じかわかります。つまり2回計算すると一致するかわかります。
量子コンピュータを使う場合
**固有のアルゴリズムを適用させることができ、1回の計算ですみます!**これが量子コンピュータのすごいところです。仮に1兆桁計算するのに50年かかるとすれば、普通なら2回計算で100年かかるのに、量子コンピュータなら50年ですみます。生きている間に結果がわかります。**と一般には言われることが多いですが現実的には2回必要です。**あれ量子コンピュータ使う意味なくね?ですが他のアルゴリズムでは劇的に差が出るので量子コンピュータは流行っているのです。ドイチュの問題は実用性はないが理解にはもってこいのアルゴリズムとして教科書等に記載されているのです。
ドイチュの問題の準備
ドイチュの問題の肝の部分の演算はたった2ビットですみます。現実的には、平方根の2進数展開の1兆桁目を計算するのに補助的なビットは必要ですが、いきなり具体化すると煩雑になるためまずは関数f(x)を使うことでお茶を濁し、肝の2ビット部分のみの解説とします。(詳細な議論は次の記事でやるつもりなので御心配なく)まずは関数f(x)を以下のように定義します。
f(x) = (√(x+2)を2進数展開した1兆桁目の値)
関数の入力であるxは0か1の値を取り、f(x)も当然0か1の値を取ります。例えばx=0の時は√2の2進数展開の1兆桁目の値がf(x=0)となりx=1の時は√3の2進数展開の1兆桁目の値がf(x=1)となります。
肝の2ビットには、このf(x)の値を用いて作用する次のような演算子を定義しましょう。
これは1ビット目の値xより計算されたf(x)を2ビット目に排他的ORのような感じで作用させることを意味します。2ビット目の「マル+」の記号がそうです。あるいは同じ結果になりますが2を法とした和を意味します。具体的には基本足し算ですが1+1=10(2進数)のように繰り上がる場合は一の位の0が計算結果になります。
この「マル+」記号は次のように考えても良いでしょう。そしてこちらのほうが便利です。すなわち、f(x)の値が1になった時はyの値を反転させ、0の時は何もしない、ということです。cNOT演算に似ています。y「マル+」f(x)の計算結果を具体的に書き下しましょう。
f(x)=0 y=0 → 0
f(x)=0 y=1 → 1
f(x)=1 y=0 → 1
f(x)=1 y=1 → 0
ドイチュの問題を解くアルゴリズムの肝の部分
ここまでくればドイチュの問題を理解する準備は整いました。まずは最初のビットとして次のビットを用意します。
|1>|1>
これの1ビット目と2ビット目の両方にアダマール変換を作用させます。アダマール変換については超基礎 量子コンピュータのための量子論をご覧ください。
H×Hという演算子がありますがこれは1ビット目に左側のHを作用させて2ビット目に右側のHを作用させるということです。
次に、こうしてできた状態の和にf(x)の値を用いた演算子Ufを作用させます。
f~(x)という記号がありますがこれはf(x)が0なら1に、1なら0に、値を反転させたものです。
ここで煩雑な式になってしまったので整理します。f(0)=f(1)だと仮定しましょう。つまり1兆桁目の数字が一致する場合にどうなるか解析します。ちなみに当然この時f~(0)=f~(1)です。式を整理すると次のようになります。
この1ビット目に再びアダマール変換を施すと次のようになります。
一方、f(0)≠f(1)の場合、つまり1兆桁目の数字が一致しない場合を考えます。この時当然f(0)=f~(1)です。整理すると次のようになります。
1ビット目にアダマール変換を作用させます。
式がすっきりしました。二つは似たような計算結果になりましたね。
ドイチュの問題の計算結果の解説
いま、わたしたちはf(0)とf(1)が同じ場合と異なる場合で分けて考えました。でもそんなことせず、Ufを作用させた後にアダマール変換を1ビット目に作用させて、1ビット目を測定した場合を考えましょう。上の結果はもしf(0)=f(1)なら測定結果としては1が得られることを意味しており、逆にf(0)≠f(1)なら0が得られることを意味しています。つまり最終的な1ビット目の状態を測定するだけでf(0)=f(1)か否かわかるということです。
なぜこのようなことができたのか整理しましょう。重要なのが、最初に用意した|1>|1>というビットにアダマール変換を行ったことです。これにより状態は|0>|0>、|0>|1>、|1>|0>、|1>|1>、のすべての状態の和になりました。ここにUfを作用させることで、すべてのパターンを「並列的に」計算させ、再度アダマール変換で1ビット目を元に戻しその値が0か1かでf(0)とf(1)が一致するか判別したのです。そして重要なのはこの時、Ufは状態にたった1回しか作用させていないということです。これは、50年かかる計算を1回しか実行していないことに相当します。これが俗に言う「量子コンピュータは並列的に計算することができ、計算速度を圧倒的に向上させることができる」という意味です。
ちなみにここまで来て、「ん?騙されてない私?」と思った人、あなたの感覚は正しいです。まずそもそも「並列的に」計算という言葉の意味が曖昧です。並列的に計算したら、すべての計算結果が得られることを期待したくなります。しかし今回はf(0)=f(1)か否かしか分からず、f(0)の値も、f(1)の値も分からないのです。1回計算しているにもかかわらずです。状態の和を用いて演算する事で、普通のコンピュータではありえない計算をし、特殊な結果を得ることができるのですが、すべての情報が得られるわけではなく、むしろ見えなくなる情報もあるのです。しかしそれでもなお、暗号解読や量子化学計算など、量子コンピュータを使うと圧倒的に早く欲しい情報が手に入る事例もあるため、研究されているのです。
ちなみに、騙されている箇所がもう一箇所あります。冒頭でも話したようにf(x)に関連した部分を現実的には2回は呼び出す必要があります。これはf(x)自身を計算するために付加的に必要なビットが存在しますが、その付加的ビットと1ビット目を量子演算子を作用させたあと、1ビット目を元に戻すという操作が必要になるためです。詳細は次の記事で話します。
まとめ
- 量子コンピュータの最初のアルゴリズムにドイチュの問題がある。
- ドイチュの問題は√2の2進数展開のした小数以下1兆桁目と√3の同じく1兆桁目が一致するか否かを判定する問題と等価である
- 普通のコンピュータなら2回1超桁目を計算する必要あるが、量子コンピュータなら1回の計算で済む
- と一般的には言われているが本当は2回必要
- 2回必要なのは量子コンピュータ全てのアルゴリズムに共通の事実だが、他のアルゴリズムでは2倍どころのスピードアップではないため、量子コンピュータが優位な事実は変わらない
- 量子コンピュータだからといってその問題に関する「あらゆる計算結果」が同時に得られるわけではない