はじめに
私はルービックキューブを速く解くスピードキューブという競技を趣味としているハードウェア/ソフトウェアエンジニアのNyanyan(にゃにゃん)です。今回はパソコン甲子園2014のFloppy Cubeという問題を解説し、そこからルービックキューブなどの立体パズルを解くプログラムの汎用的な書き方を解説します。
私は現在2x2x2のルービックキューブを(おそらく)世界最速で解くロボットを作っていて、そこで培った知識を使ってこの問題が解けました。この知識はこの問題にはオーバーキルなものなのですが、ぜひ紹介したいと思いこの記事を書いています。
問題の概要
フロッピーキューブとは

写真のようなパズルです。「一段しかないルービックキューブ」と呼ばれることもあり、まあその通りです。ポイントとして、軸が4つ(上下左右)ありそれを180度回転することで揃えることができるということがあります。
英語版wikiによると、組み合わせ数は$192$(普通のルービックキューブが$4.3\times10^{19}$通りであることを考えるとかなり少ないです)、神の数字(最大でも$N$手あれば必ず揃えられるという数字)は$8$です。
問題
問題文の全文はこちら
フロッピーキューブの各面の色の状態が数字の羅列として与えられるので、この状態から何手で揃えられるかを出力してください。
メモリ制限は$131072$KB、時間制限は$1$秒で、最大30個のパズルの状態が与えられます(つまりパズル1つあたり平均$33$ms以内に答えを出力しなくてはいけません)。
パズルの状態は数字の羅列で与えられます。この数列はパズルのステッカー(色がついているところ)の数である$30$(表面と裏面で$9$個$\times 2=18$、側面が$3$個$\times4=12$で合計$30$)の要素で構成されていて、それぞれ色が数字$1,2,3,4,5,6$で表されています。この色を表す数字のうち$1,3$は表面/裏面の色で、それ以外は側面の色です。
この色を表す配列を$p$とすると、$p$の($0$始まりでの)番号と面の対応は以下の図の通りになります。
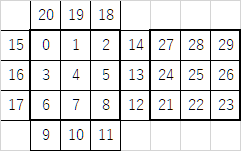
揃っている状態はサンプルケースにあるこちらです。
1 1 1 1 1 1 1 1 1 2 2 2 4 4 4 6 6 6 5 5 5 3 3 3 3 3 3 3 3 3
入力は以下のように与えられます。
入力されるパズルの数 N (<=30)
空白区切りのパズルの状態数列 p_1
p_2
...
p_n
では問題を解いていきましょう。
直感的だが汎用性は低い方法
まず最初に思いつくであろう方法は、愚直にシミュレーションし幅優先探索する方法です。汎用性は低いですが比較的簡単に実装できます(ただし回転のシミュレーションをするのがとてもだるいです)。
パズル一つの計算量を見積もります。各状態に対して次に回せる手は上下左右のどれかを$180$度回すことなので、$4$通りあります(このあとここを工夫してさらに計算量を削減します)。そして最大でも$8$手で揃うので、計算量は最大でも
$O(4^8)=O(6.6\times10^4)$
となります。パズルの状態が30個与えられても計算量は$O(2.0\times10^6)$となり、間に合いそうです。
さて、この方法で面倒なのはパズルを実際に動かすところの実装です。今回は回転という動作を、入力される数列$p$自体を操作することで表現します。この方法は面倒かつ汎用性が皆無なのであとで違う方法を使います。
フロッピーキューブは必ず$180$度回転を用いるため、2つのステッカー(数列の要素)を適切に選んでスワップすることで実装できます。
実装した結果はこちら(コードはリンク先をご覧ください)です。一応ACしました。実行時間は$0.35$秒、メモリ使用量は$14580$KBでした。
この方法の良い点
1, どことどこをスワップさせるかを間違えずに実装できればあとはただ幅優先探索を行うのみなので考え方としては簡単
この方法の悪い点
- どことどこをスワップさせるかの実装が非本質的かつだるい(私も間違えました)
- 幅優先探索なのでメモリをそれなりに使う
- 汎用性がない(普通のルービックキューブを解くプログラムをこの方法で書くと回転の実装がとてもだるくなる)
直感的な方法の改良
さて、先程のプログラムを改良していきましょう。実はこのプログラムは計算量を簡単に削減できます。
直前に回したのと同じ手は回さない
例えば直前に上、下と回したあと上を回さない
7手で揃わなかったら答えは必ず8(8手以内に必ず揃うので)
この3つを実装すると、計算量が削減できます。具体的にパズル一つについての計算量を見積もってみましょう。最大(8手で揃う)場合で考えます。(※数学的に厳密でないです。実際はこれより若干計算量が増えそうです)
$O(4\times3^6-2\times5\times3^4)=O(2.1\times10^3)$
先程のプログラムの計算量が$O(6.6\times10^4)$だったのでかなり削減できました。
やってみた結果はこちらです。実行時間は$0.08$秒、メモリは$6704$KBでした。時間もメモリもかなり改善されました(先程のコードでもACですが)。
汎用的な方法を考える
概要
天下り的ですが、汎用的な方法として以下のようなパズルの記述方法があります(ルービックキューブを嗜む人はご存知かもしれません)。
- ステッカーごとでなくパーツごとに考える
- パーツの位置と向きに注目して考える
- パズルはいくつかの形状のパーツで構成されているので、パーツの形状ごとに上記の方法を考える
今回のフロッピーキューブで具体的に考えましょう。

フロッピーキューブでステッカーがついている(色がついている)パーツは「コーナー」「エッジ」「センター」の3種類です。それぞれについてもう少し考えてみましょう。
コーナー
回転させると移動する。
回転させると向き(裏表)が変わる
エッジ
回転させても移動しない(エッジパーツを軸に回るので)
回転させると向き(裏表)が変わる
センター
回転させても移動しない
回転させても向きが変わらない
これらの事実を考慮すると、パズルの状態を表すには以下の3種類の情報があれば良いことがわかります。
- コーナーパーツ4つそれぞれの位置 (CP=Corner Permutationと言う)
- コーナーパーツ4つそれぞれの向き (CO=Corner Orientationと言う)
- エッジパーツ4つそれぞれの向き (EO=Edge Orientationと言う)
追記 厳密な証明はできていませんが、どうやらCPが揃えばCOは自動的に揃うようです。記事内ではCOも考慮した書き方のままにしておきますが、COを考慮しない提出リンクも追記として貼っておきます。
実際の回転処理では、以下のような規則で配列をいじります。
位置
コーナーパーツの位置(左上、右上、右下、左下)にそれぞれ0から4までの番号(名前)をふる。
コーナーパーツ自身にも0から4までの番号をふる。
例えばCP配列cpのi番目の要素cp[i]は、場所iにあるパーツがcp[i]という名前という意味になります。
向き
コーナー/エッジパーツの位置にそれぞれ0から4の番号をふる。
例えばパーツが表面を向いている(揃ったときに向いている方向)ときは0、裏面を向いているときは1とする。
例えばCO配列のi番目の要素co[i]が0ならば場所iにあるパーツは表を向いていて、1ならば裏を向いていることになります。
実装
一つのパズルの状態につき複数の配列で状態を表すので、クラスを使うと楽です。
また、パーツの位置にふる番号を例えば時計回りに設定することで、回転させる処理を書く際にどこが動くのかを手打ちする必要がなくなります。
この方法の欠点は、入力される各ステッカーの色の情報をCP、CO、EOの3つの配列に変換するのが多少面倒だということです。
結果
私が書いたコードと実行結果はこちらです。実行時間は$0.12$秒、メモリ使用量は$6860$KBでした。
追記 COを考慮しないプログラムでもACしました。提出リンクはこちらです。実行時間は$0.09$秒、メモリ使用量は$6776$KBでした。
計算量を削減する - 枝刈り
ここでは先程の汎用的なコードの利点である汎用さを使って前計算を行い、それを使って枝刈りをして計算量を削減しましょう。
枝刈りは、神の数字である8手以内に揃わないとわかっている状態になったら探索を打ち切るようにして実現します。具体的にはCP、CO、EOのそれぞれすべての状態について何手でCPならCPだけ、COならCOだけ、EOならEOだけを揃えられるかを前計算しておきます。そして幅優先探索の最中に、
今まで回した手数 + CP、CO、EOをそれぞれ単独で揃えるために必要な最大の手数
を計算し、これが神の数字である8手を超えたらこのノード(状態)についてこれ以上の探索を打ち切ります。
これを実装した提出結果はこちらです。実行時間は$0.16$秒、メモリ使用量は$6804$KBでした。
追記 COを考慮しないプログラムでもACしました。提出リンクはこちらです。実行時間は$0.13$秒、メモリ使用量は$6544$KBでした。
この枝刈りの手法は事前計算を行うことと、毎回の探索でCP、CO、EOの配列それぞれの固有番号を計算するため、今回のように
- 一つのノード(状態)から回せる次の手の数が少ない
- 最大の探索深さ(つまり神の数字)が浅い(小さい)
ときには恩恵はあまりありません。今回は実行時間が少しのびてしまいました。しかし、フロッピーキューブよりも複雑なパズルを解こうとする場合にこの枝刈りは計り知れない恩恵があります。
メモリ使用量を削減する - IDA*
ここでお話しする内容は、フロッピーキューブでない何か別のパズルを解く際に幅優先探索を使うとメモリ使用量がとんでもないことになってしまうことへの対処法です。例として2x2x2ルービックキューブで幅優先探索を行うと、私の書いたプログラムでは4GB程度のメモリを食ってしまいました。
ここで出てくるのがIDA*という探索法です。詳しくはこちらの記事が詳しくておすすめです。こちらの記事から一部を引用して紹介します。
IDAを一言で表すと、「最大深さを制限した深さ優先探索(DFS)を、深さを増やしながら繰り返す」です。
IDAのからくりは、一度探索したノードを忘れることにあります。ノードを忘れてしまえば、メモリを解放できますよね。
IDA*では深さ$N-1$までで深さ優先探索を行って解が見つからなかったら、最大深さを$N$に増やしてまた一から探索をやり直します。こうすることで、
- 返される結果は必ず最短手数(実装を少しいじれば最短手順も出力できます)
- メモリ使用量がとても少ない
という恩恵があります。
ただし、深さの浅いノード(状態)については何度も同じ探索を繰り返してしまうため、計算量は若干増大します。しかしパズルの状態は深さに対して指数関数として増大するため、計算量の増大はそこまで大きくありません。
具体的に今回の場合の計算量を見積もってみましょう。7手で揃うパズルの状態であるとします。幅優先探索を行った場合は、枝刈りを無視すると計算量は大体$O(2.1\times10^3)$でした。そしてIDA*では、
$O(\Sigma_{i=1}^7 (4\times3^{i-1}-2\times(i-2)\times\mathrm{floor}(3^{i-3})))=O(3.3\times10^3)$
です。比較するとそこまで大きな差は見られません。
実装した結果はこちらです。実行時間は$0.09$秒と、なんと先程のプログラムよりも速くなりました。メモリ使用量は$6044$KBと、幅優先探索の$6544$KBから削減できました。
追記 COを考慮しないプログラムでもACしました。提出リンクはこちらです。実行時間は$0.07$秒、メモリ使用量は$6036$KBでした。
まとめ
ここまで読んでくださりありがとうございます。
特に後半に紹介した方法はとても汎用的な方法ですがフロッピーキューブに対してはあまりにもオーバーキルな方法です。ぜひとも2x2や3x3のルービックキューブを解くプログラムをこの方法で書いてみてこの方法の汎用性の高さを実感してください。
2x2については私が書いたルービックキューブを解くロボットを作ろう!2 アルゴリズム編という記事、3x3は7y2nさんのルービックキューブを解くプログラムを書いてみよう(中編:IDA*探索)という記事をおすすめします。