Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@Nuts12

CRISP-DM / 機械学習 / 回帰モデル（EDAからアンサンブル学習まで）

Last updated at Posted at 2024-03-02

[Python] 初心者が回帰モデルで機械学習をCRISP-DMの流れで学んでみた（EDAからアンサンブル学習まで）


はじめに

こんにちは。Qiita初投稿・リスキリングを目的にプログラミングを学びなおしている元プログラマー（現なんちゃってプロジェクトマネージャー）の @Nuts12 です。
現在私はIT企業に勤めながら、Aidemyというプログラミングスクールで夜な夜なPythonと機械学習に取り組んでいます。 本投稿はAidemy Premiumのカリキュラムの一環で、受講修了条件を満たすために公開しているものです。 少々長文となっておりますが、ご了承いただけると幸いです。

開発環境について

以下、今回の開発環境になります。
Python: Python 3.9.13
開発ツール: VSCode

使用したライブラリ、モジュール一覧:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import preprocessing
from sklearn.decomposition import PCA
from sklearn.metrics import mean_squared_error as MSE
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.linear_model import ElasticNet
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.svm import SVR
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.svm import LinearSVR
from sklearn.ensemble import BaggingRegressor
from sklearn.ensemble import AdaBoostRegressor
import lightgbm as lgb
from sklearn.neural_network import MLPRegressor
import optuna
from sklearn.model_selection import cross_val_score
import xgboost as xgb
ライブラリのバージョン：
numpy: 1.26.3
pandas: 2.1.4
matplotlib: 3.8.2
seaborn: 0.13.1
sklearn: 1.3.2
lightgbm: 4.3.0
optuna: 3.5.0
xgboost: 2.0.3

学習の流れ

今回は機械学習のプロセスを実践を見据えてCRISP-DM(CRoss-Industry Standard Process for Data Mining)の流れに沿って実施してみました。Wikipediaによると、CRISP-DMとはデータマイニングの専門家が使用している、オープンな標準プロセスモデルで、最も広く使用されている分析モデルです。CRISP-DMには以下の６つのプロセスがあります。順番に並んでいますが、実際は３.データ準備と４．データモデリングの間を行ったり来たり試行錯誤しながら進むことになります。今回の学習は基本この流れに倣って進めていきます。
ただし、６.適用プロセスについては対象がないので今回は割愛いたします。

  1. ビジネス理解
  2. データ理解
  3. データ準備
  4. モデリング
  5. 評価
  6. 適用

データ選定の背景

これまで学んできたデータ分析手法を用いて、今の自分のスキル＋αをアウトプットすることを目標に、分析に使用するデータを以下の基準で選択いたしました。

  1. 教師あり学習、回帰モデル用のデータサンプルであること
  2. データ件数が10,000件以上相当あること
  3. 特徴量が10～20程度であること

機械学習で使用できるデータソースを探し始めるとKaggleをはじめ、今は様々なサイトでデータがダウンロードできるようになっており、どれが今の自分にとって最適なのか目移りしてしまい非常に迷いましたが、とりあえずやってみなければ始まらないと決めたのがthe UC Irvine Machine Learning Repositoryからダウンロードしてきた以下のデータソースです。

Bike Sharing Dataset

データはレンタルバイクの1時間ごとの台数と1日ごとの台数、それに対応する天候と季節の情報となっており、データ数が、17,389件、特徴量が13、そして回帰用データということで探していた条件を充足していたので、こちらのデータで作業にとりかかることとしました。

機械学習開始

以降、CRISP-DMのプロセスに従い分析を実施しました。

１．ビジネス理解

まずは、ビジネス理解です。本プロセスでは、ビジネスにおける課題を明確にし、データ分析プロジェクトの計画を策定します。レンタルバイクビジネスには全く縁も所縁もなかったので、とりあえずHP上のデータセットの説明より、業界の動向を読み取ってみました。

バイク・シェアリング・システムは、会員登録からレンタル、返却まで全てのプロセスが自動化された、従来のレンタサイクルの新世代のシステムである。これらのシステムを通じて、利用者は特定の位置から簡単に自転車を借り、別の位置で返却することができる。現在、世界中に約500以上のバイクシェアリング・プログラムがあり、その数は50万台以上にのぼる。今日、交通、環境、健康問題において重要な役割を担っているため、これらのシステムに大きな関心が寄せられている。

自転車シェアリングシステムの興味深い実世界での応用とは別に、これらのシステムによって生成されるデータの特徴が、研究にとって魅力的なものとなっている。バスや地下鉄のような他の交通サービスとは異なり、これらのシステムでは移動時間、出発と到着の位置が明確に記録される。この特徴により、自転車シェアリング・システムは仮想センサー・ネットワークとなり、都市におけるモビリティのセンシングに利用できる。したがって、これらのデータを監視することで、都市における重要な出来事のほとんどを検知できることが期待される。

ふむふむ。自転車シェアリングデータを使って、都市のモビリティセンシングを行い、「スマートシティの構築や交通システムの最適化、ユーザーエクスペリエンスの向上などに活用すること」 が本分析の目的であると解釈しました。高々、自転車シェアリングとたかを括っていたが壮大な目的があるらしい。それでは本目的を遂行するため実践で使えるレベルの分析をしてやろうじゃないかと次のステップに進むこととしました。

２．データ理解

このデータはHP上に詳細情報が掲載されているので、実データを見る前に確認してみる。

＃ Variable Name Role Type Description(JP) Missing Values
1 instant ID Integer レコードインデックス no
2 dteday Feature Date 日付 no
3 season Feature Categorical 1:冬、2:春、3:夏、4:秋 no
4 yr Feature Categorical 年（0：2011年、1：2012年） no
5 mnth Feature Categorical 月（1～12） no
6 hr Feature Categorical 時間（0～23） no
7 holiday Feature Binary その日が休日かどうか (http://dchr.dc.gov/page/holiday-schedule から抽出) no
8 weekday Feature Categorical 曜日 no
9 workingday Feature Binary 土日祝日でない場合は1、そうでない場合は0 no
10 weathersit Feature Categorical 1: 快晴, 雲が少ない, 部分的に曇り, 部分的に曇り
2：霧＋曇り、霧＋雲切れ、霧＋雲少、霧
3: 小雪、小雨+雷雨+雲が散らばる、小雨+雲が散らばる
4：大雨＋氷霰＋雷雨＋霧、雪＋霧		 no
11 temp Feature Continuous 正規化した気温（摂氏）。値は、(t-t_min)/(t_max-t_min), t_min=-8, t_max=+39 (1時間単位のみ)で求められる。 no
12 atemp Feature Continuous 摂氏で正規化した体感温度。値は、(t-t_min)/(t_max-t_min)、t_min=-16、t_max=+50 (1時間単位の場合のみ)。 no
13 hum Feature Continuous 正規化湿度。値は100（最大）に分割される。 no
14 windspeed Feature Continuous 正規化風速。値は67（最大）に分割される。 no
15 casual Other Integer カジュアルユーザー数 no
16 registered Other Integer 登録者数 no
17 cnt Target Integer カジュアルユーザーと登録ユーザーを含むレンタルバイク総台数 no

丁寧にデータタイプや、特徴量、ターゲット、Nullの有無まで説明に記載されている。また、データソースは以下のとおり時間単位と日単位の2種類に分かれているとのこと。

  1. hour.csv : bike sharing counts aggregated on hourly basis. Records: 17379 hours
  2. day.csv - bike sharing counts aggregated on daily basis. Records: 731 days

以下、この説明をみて思ったこと。これらは実際のデータを見て確認することにしよう。
・Null値はないとのことだが、確認は必要
・時間単位のデータと日単位のデータは日付でマージできそうだが、マージした際、歯抜けになったデータをどう処理するか？
・気温と体感気温とはほとんど同じとならないだろうか？
・気温と体感気温の単位は両方とも華氏
・時系列データだが2年間分のデータなのでトレンドまでは追わなくてもよさそう
・季節のデータは月に包含されるので不要ではないだろうか？

それでは、実際に2本のデータをダウンロードしてソースから読み込んでみる。データを読み込んで、いつもの流れで shape、dtypes、head、tail、describeを実行。

データ取込み
# Day/hour データ読み込み
day_df = pd.read_csv('./day.csv')
hour_df = pd.read_csv('./hour.csv')

# 日データの
# データの形を表示
print( f'day_df_shape : {day_df.shape}\n' )

# データの各columnのデータ型を表示
print( f'{day_df.dtypes} \n' )

# データの先頭5つを可視化
print( day_df.head() )

# データの最後から5つを可視化
print( day_df.tail() )

# 数値データの統計量を表示
print(day_df.describe().T)

まず着手したのが、日データと時間データのマージ作業です。
時間データの各カラムについて日データとの突合せのキーとなる日付データのdtedayカラムでgroupbyして、集計データを作成し、日データとの突合せを粛々と行っていったわけですが、結論から言うと、時間データは、日データと同じデータであること、つまり単純に日データを時間で分割（サブセット）したものが、時間データであることが確認していく中で判明しました。
マージ作業にそれなりに時間をかけていたので、マージ完了後、日データと時間データのcntの合計が合致したときは少々愕然としたわけですが、教訓として、データソースの情報があらかじめ与えられている場合は隅々まで読み込んでおくこと、また、データのマージが必要な場合は実務的にはExcelで加工してしまった方が早い場合があるということを学べたわけです。

時間データ(hour.csv)が日データ(day.csv)のサブセットであるため利用不要となったので、分析は日データ(day.csv)のみで行うこととしました。データ件数は日データの731件となってしまい、当初想定していたデータ量より大幅に少なくなってしまいましたが、ここまで来たので後戻りするのではなく先に進めることとしました。改めてデータ理解のフェーズの最初に戻って今後の手順を整理します。

  1. データの可視化
  2. 欠損値の確認
  3. 重複行の確認
  4. 外れ値の確認
  5. データ分布の確認
  6. データ相関性の確認

２－１．データの可視化

データの可視化
# Day データ読み込み
day_df = pd.read_csv('./day.csv')

# 日次データの
# テストデータの形を表示
print( f'day_df_shape : {day_df.shape}\n' )

# 日次データの各columnのデータ型を表示
print( f'{day_df.dtypes} \n' )

# 日次データの先頭5つを可視化
print( day_df.head() )

# 日次データの最後5つを可視化
print( day_df.tail() )

# 数値データの統計量を表示
print(day_df.describe().T)

>>> 出力結果
day_df_shape : (731, 16)

instant         int64
dteday         object
season          int64
yr              int64
mnth            int64
holiday         int64
weekday         int64
workingday      int64
weathersit      int64
temp          float64
atemp         float64
hum           float64
windspeed     float64
casual          int64
registered      int64
cnt             int64
dtype: object

   instant      dteday  season  yr  mnth  holiday  weekday  workingday  weathersit      temp     atemp       hum  windspeed  casual  registered   cnt      
0        1  2011-01-01       1   0     1        0        6           0           2  0.344167  0.363625  0.805833   0.160446     331         654   985      
1        2  2011-01-02       1   0     1        0        0           0           2  0.363478  0.353739  0.696087   0.248539     131         670   801      
2        3  2011-01-03       1   0     1        0        1           1           1  0.196364  0.189405  0.437273   0.248309     120        1229  1349      
3        4  2011-01-04       1   0     1        0        2           1           1  0.200000  0.212122  0.590435   0.160296     108        1454  1562      
4        5  2011-01-05       1   0     1        0        3           1           1  0.226957  0.229270  0.436957   0.186900      82        1518  1600      
     instant      dteday  season  yr  mnth  holiday  weekday  workingday  weathersit      temp     atemp       hum  windspeed  casual  registered   cnt    
726      727  2012-12-27       1   1    12        0        4           1           2  0.254167  0.226642  0.652917   0.350133     247        1867  2114    
727      728  2012-12-28       1   1    12        0        5           1           2  0.253333  0.255046  0.590000   0.155471     644        2451  3095    
728      729  2012-12-29       1   1    12        0        6           0           2  0.253333  0.242400  0.752917   0.124383     159        1182  1341    
729      730  2012-12-30       1   1    12        0        0           0           1  0.255833  0.231700  0.483333   0.350754     364        1432  1796    
730      731  2012-12-31       1   1    12        0        1           1           2  0.215833  0.223487  0.577500   0.154846     439        2290  2729    
            count         mean          std        min          25%          50%          75%          max
instant     731.0   366.000000   211.165812   1.000000   183.500000   366.000000   548.500000   731.000000
season      731.0     2.496580     1.110807   1.000000     2.000000     3.000000     3.000000     4.000000
yr          731.0     0.500684     0.500342   0.000000     0.000000     1.000000     1.000000     1.000000
mnth        731.0     6.519836     3.451913   1.000000     4.000000     7.000000    10.000000    12.000000
holiday     731.0     0.028728     0.167155   0.000000     0.000000     0.000000     0.000000     1.000000
weekday     731.0     2.997264     2.004787   0.000000     1.000000     3.000000     5.000000     6.000000
workingday  731.0     0.683995     0.465233   0.000000     0.000000     1.000000     1.000000     1.000000
weathersit  731.0     1.395349     0.544894   1.000000     1.000000     1.000000     2.000000     3.000000
temp        731.0     0.495385     0.183051   0.059130     0.337083     0.498333     0.655417     0.861667
atemp       731.0     0.474354     0.162961   0.079070     0.337842     0.486733     0.608602     0.840896
hum         731.0     0.627894     0.142429   0.000000     0.520000     0.626667     0.730209     0.972500
windspeed   731.0     0.190486     0.077498   0.022392     0.134950     0.180975     0.233214     0.507463
casual      731.0   848.176471   686.622488   2.000000   315.500000   713.000000  1096.000000  3410.000000
registered  731.0  3656.172367  1560.256377  20.000000  2497.000000  3662.000000  4776.500000  6946.000000
cnt         731.0  4504.348837  1937.211452  22.000000  3152.000000  4548.000000  5956.000000  8714.000000

事前に確認していた情報のとおり、データは731件、カラム数は16、データ型についてはdtedayだけがオブジェクト型(YYYY-MM-DD形式の日付文字列)で他は数字になっていることを確認。日付は2011-01-01から2012-12-31まできっちり2年分入ってそう。

統計データについては、量的データ、比例尺度となっている、temp、atemp、hum、windspeedに着目して確認してみたが、特段気になる点は見当たらない。これについては後程可視化して検証する方針とする。

２－２．欠損値の可視化

事前の情報で欠損値がないことは分かっているが、念のため確認。

欠損値確認
#
#  欠損値確認
# 

print('Null値確認')
print(day_df.isnull().sum())
print('na値確認')
print(day_df.isna().sum())

>>> 出力結果
Null値確認
instant       0
dteday        0
season        0
yr            0
mnth          0
holiday       0
weekday       0
workingday    0
weathersit    0
temp          0
atemp         0
hum           0
windspeed     0
casual        0
registered    0
cnt           0
dtype: int64
na値確認
instant       0
dteday        0
season        0
yr            0
mnth          0
holiday       0
weekday       0
workingday    0
weathersit    0
temp          0
atemp         0
hum           0
windspeed     0
casual        0
registered    0
cnt           0
dtype: int64

確かにNull値、na値が存在していないことを確認。

２－３．重複行の確認

重複行の確認
#
#  重複行確認
#

print('重複行値認')
print(day_df.duplicated().sum())

>>>出力結果
重複行値認
0

重複行がないことを確認。

２－４． 外れ値の確認

四分位範囲で外れ値を確認していく。対象としたのは量的データ、比例尺度となっているtemp、atemp、hum、windspeedの４データ。

外れ値の確認
#
#  外れ値確認
# 

# 外れ値にマーキングの為Noneを設定する
def outlier_adj(df):
    
    for i in range(len(df.columns)):

        # 列を抽出する
        col = df.iloc[:,i]

        # 四分位数
        q1 = np.percentile(col, 25)
        q3 = np.percentile(col, 75)
        iqr = q3 - q1 #四分位範囲

        # 外れ値の基準点
        outlier_min = q1 - (iqr) * 1.5
        outlier_max = q3 + (iqr) * 1.5

        # 範囲から外れている値を除く
        col[col < outlier_min] = None
        col[col > outlier_max] = None

    return df

# 確認用tempデータ
day_df_num = day_df.loc[:, ['temp','atemp','hum','windspeed']]

# 箱ひげ図を表示
sns.boxplot(data=day_df_num)
plt.show()

# 確認のため例外値にNoneを設定
day_df_num = outlier_adj(day_df_num)

# null値確認
print('Null値確認')
print(day_df_num.isnull().sum())

>>> 出力結果
Null値確認
temp          0
atemp         0
hum           2
windspeed    13
dtype: int64

出力された箱ひげ図
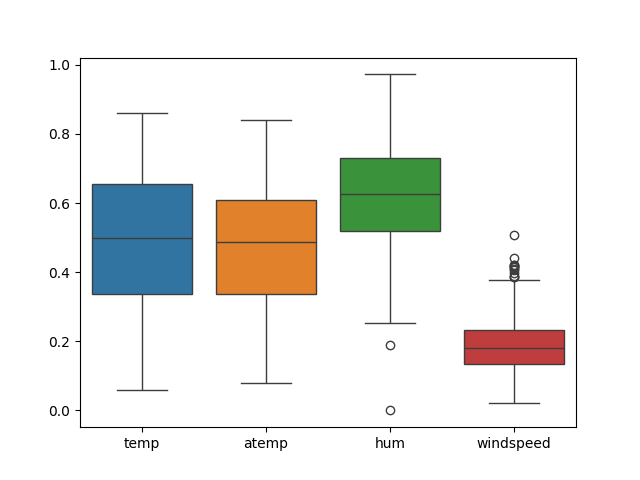
Figure_0.png
確認の結果humで2行、windspeedで13行の外れ値があることを把握。

２－５．データ分布の確認

各特徴量毎にデータの偏りを確認していく。

seasonとmnthの関連性確認

seasonとmnthの関連性確認
# seasonとmnthの関連性確認
print(pd.crosstab(day_df['season'], day_df['mnth']))

>>> 出力結果
mnth    1   2   3   4   5   6   7   8   9   10  11  12
season
1       62  57  40   0   0   0   0   0   0   0   0  22
2        0   0  22  60  62  40   0   0   0   0   0   0
3        0   0   0   0   0  20  62  62  44   0   0   0
4        0   0   0   0   0   0   0   0  16  62  60  40

この結果よりseasonはmnthで一位に確定できない。例えば、3月は1(冬)と2(春)が混在することから単純に月によってseasonが決まる訳ではないことを確認。

yrの可視化

yr
# yrについて可視化
sns.countplot(x='yr', data=day_df) 
plt.xlabel('yr')
plt.title('yr')
plt.show()

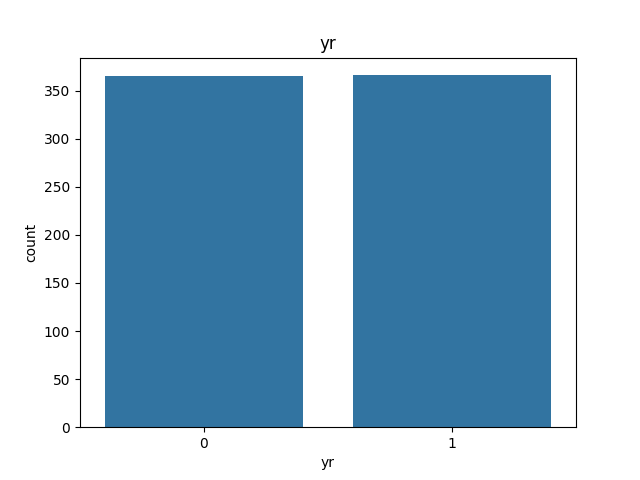
yr.png
0と1(2011年と2012年)がほぼ均等にデータがあることを確認。

seasonの可視化

season
# yrについて可視化
sns.countplot(x='season', hue='yr', data=day_df) 
plt.xlabel('season')
plt.title('season')
plt.show()

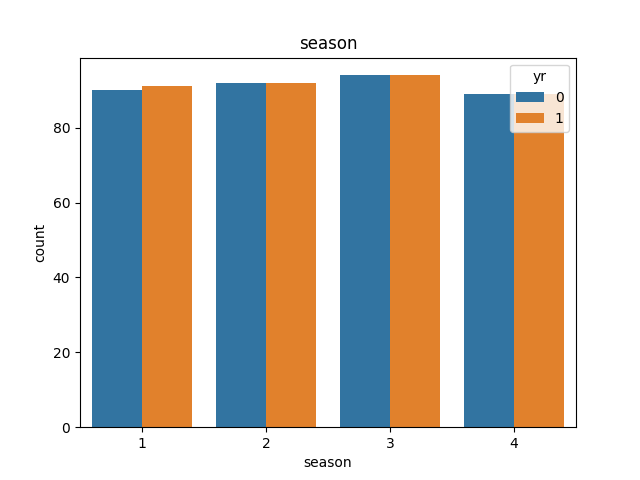
season.png
ほぼ均等にデータがあることを確認。暦の問題なので若干のデータ量の差分は気にしなくてもよさそう。

mnthの可視化

mnth
# mnthについて可視化
sns.countplot(x='mnth', hue='yr', data=day_df) 
plt.xlabel('mnth')
plt.title('mnth')
plt.show()

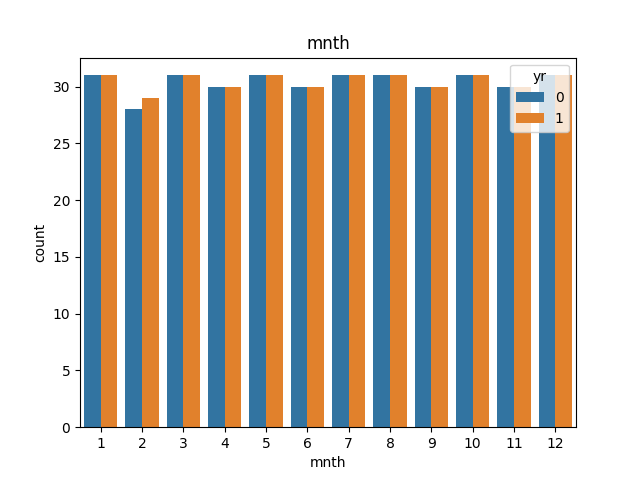
mnth.png
こちらも特に気になる点なし。各月のデータ量の違いは暦の問題と解釈。

weathersitの可視化

weathersit
# weathersitについて可視化
sns.countplot(x='weathersit', hue='yr', data=day_df) 
plt.xlabel('weathersit')
plt.title('weathersit')
plt.show()

weathersit.png
4（大雨＋氷霰＋雷雨＋霧、雪＋霧）のデータが存在していないことを確認。
こちらのデータは天候に依存するため、2011年と2012年で多少の差分があることは問題ないと判断。

２－６．データ相関性の確認

相関係数の可視化（散布図）

各特徴量の相関係数を散布図で可視化

特徴量相関散布図
# 特徴量相関散布図
sns.pairplot(day_df[['cnt','season','yr','holiday','mnth','weekday','workingday',
             'weathersit','temp','atemp','hum','windspeed']], height=1.0)
plt.show()

pairplot.png
ここからわかること。
・tempとatempに強い正の相関関係があること。
・tempとcntに弱い正の相関関係がありそう
・当たり前だが temp と mnth にも相関がありそう。

相関係数の可視化（ヒートマップ）

各特徴量の相関係数をヒートマップで可視化

特徴量ヒートマップ
# 特徴量ヒートマップ
sns.heatmap(
    day_df[['cnt','season','yr','mnth','holiday','weekday','workingday',
             'weathersit','temp','atemp','hum','windspeed']].corr(),
    vmax=1, vmin=-1, annot=True
    )
plt.show()

heatmap.png
ここからわかること。
・tempとatempに強い正の相関関係があることを数値でも確認
・tempとcntに弱い正の相関関係があることを数値でも確認
・humとweathersitに正の相関関係がみられる
・yrとcntに弱い正の相関関係があることを確認　(2011年と2012年で何が変わったのだろうか？)
・holiday、weekday、workingdayはいずれもcntとの相関関係があることを確認できる

tempとatempの相関関係を可視化

temp vs atemp
# tempとatempの相関について可視化
print(np.corrcoef(day_df['temp'], day_df['atemp']))
sns.regplot(data=day_df, x='temp', y='atemp')
plt.xlabel('temp')
plt.ylabel('atemp')
plt.title('temp vs atemp')
plt.show()

>>> 出力結果
[[1.         0.99170155]
 [0.99170155 1.        ]]

temp_atemp.png
tempとatempに、高い相関関係があることを数値とチャートの両方で確認。（外れ値を一点みつけたが見なかったことにする）

tempとcntの相関関係を可視化

tempとcntについて可視化
# tempとcntについて可視化
fig, ax1 = plt.subplots()
ax1.plot(day_df['dteday'], day_df['cnt'], label='cnt', color='blue')
ax2 = ax1.twinx()
ax2.plot(day_df['dteday'], day_df['temp'], label='temp', color='red')
h1, l1 = ax1.get_legend_handles_labels()
h2, l2 = ax2.get_legend_handles_labels()
ax1.legend(h1+h2, l1+l2, title='temp/cnt', loc='upper left')
plt.title('temp / cnt')
plt.show()

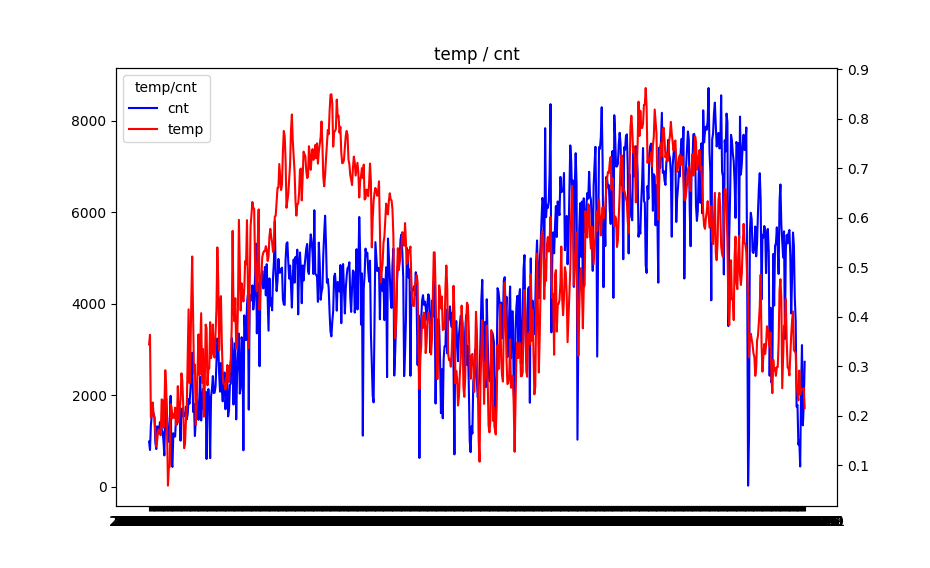
temp_cnt01.png
tempとcntを日次でプロットしてみる。２つの変数に相関があることを視覚的に確認。前半よりも後半の方で相関性が高いことが確認できる。つまり2011年は2012年より相関性が低いことがわかる。

日次で比較すると少し細かいので、月次でサマリーして確認してみる。
temp_cnt02.png

日次で確認したように相関があることを見て取れるものの、やはり2011年はtempとcntの関係性が弱くなっている。tempの方は2011年と2012年で同じような動きをしているので、何か天候とは別の要因（レンタルバイクの普及率、パンデミックや自然災害等）が cntに影響を与えているのでは等色々想定はしたものの、データが無いのでこれ以上深堀はしないことにする。

seasonとcntの相関関係を可視化

seasonとcntの相関関係を可視化
grouped = day_df[['cnt', 'yr', 'season']].groupby(['yr', 'season']).agg({'cnt':'sum'}).reset_index()
plt.figure(figsize=(10, 6))
sns.barplot(data=grouped, x='season', y='cnt', hue='yr', palette=['blue', 'green'])
plt.xlabel('season')
plt.ylabel('Sum of Value')
plt.title('Sum of Value by season')
plt.show()

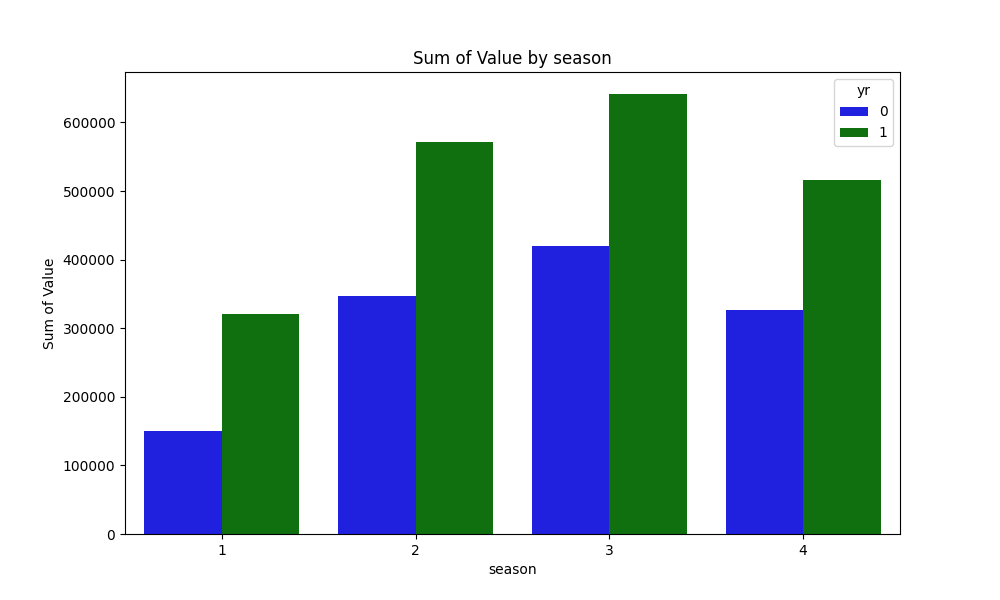
season_cnt.png
比較的に2(春)と3(夏)が高いことを確認。2011年と2012年で件数に差異があるのはtempとcntの比較時に確認済み。

mnthとcntの相関関係を可視化

mnthとcntの相関関係を可視化
grouped = day_df[['cnt', 'yr', 'mnth']].groupby(['yr', 'mnth']).agg({'cnt':'sum'}).reset_index()
plt.figure(figsize=(10, 6))
sns.barplot(data=grouped, x='mnth', y='cnt', hue='yr', palette=['blue', 'green'])
plt.xlabel('mnth')
plt.ylabel('Sum of Value')
plt.title('Sum of Value by mnth')
plt.show()

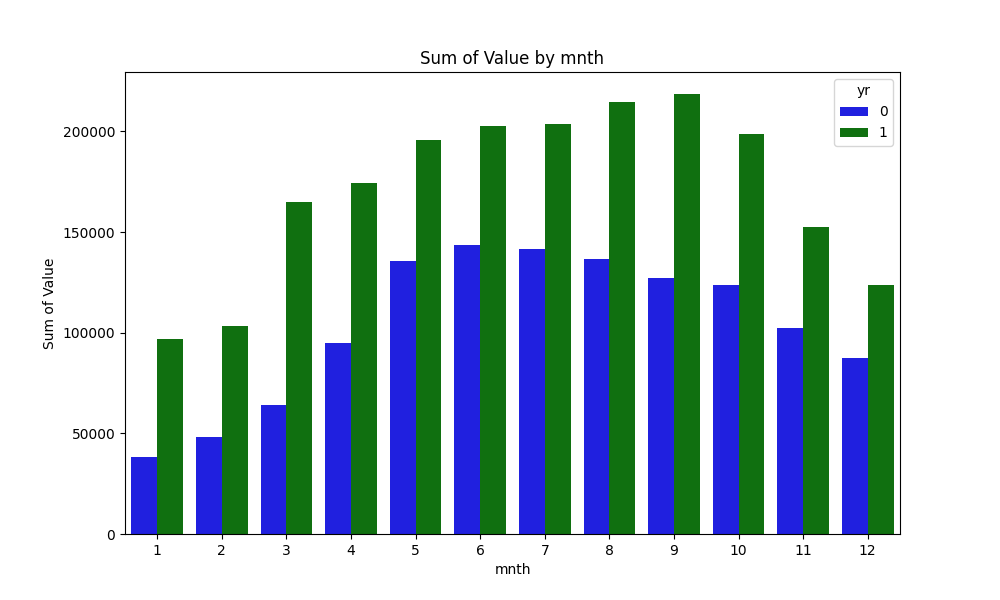
mnth_cnt.png
2011年と2012年でcntのピークの月が異なっている。それぞれ2011年は6月、2012年は9月がピーク。1月と2月はcntの減少傾向が見受けられる。寒い時期に自転車がつらいのは万国共通のようだ。2011年と2012年の件数に差異があることは確認済み。

holidayとcntの相関関係を可視化

holidayとcntの相関関係を可視化
grouped = day_df[['cnt', 'yr', 'holiday']].groupby(['yr', 'holiday']).agg({'cnt':'sum'}).reset_index()
plt.figure(figsize=(10, 6))
sns.barplot(data=grouped, x='holiday', y='cnt', hue='yr', palette=['blue', 'green'])
plt.xlabel('holiday')
plt.ylabel('Sum of Value')
plt.title('Sum of Value by holiday')
plt.show()

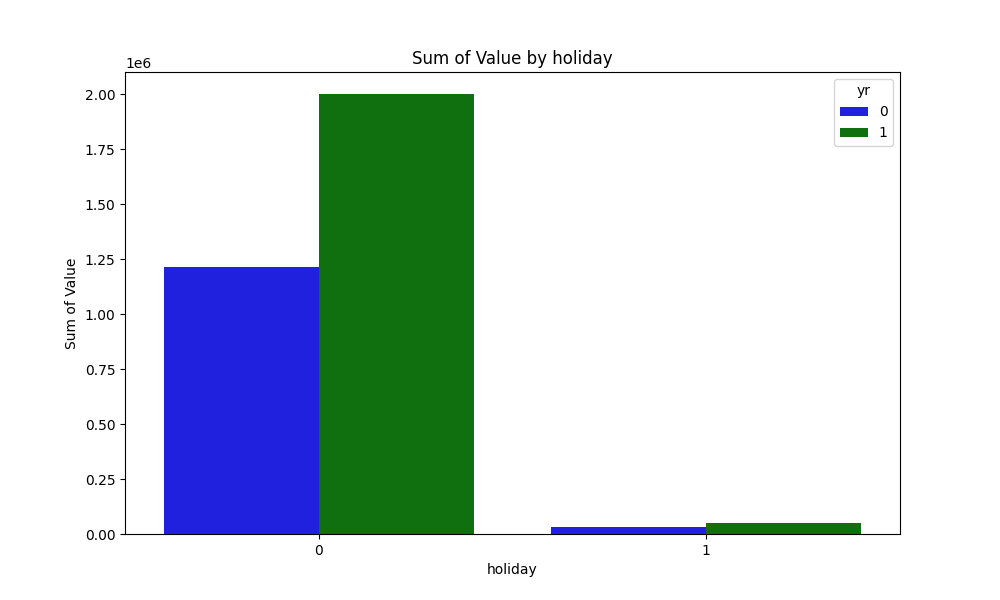
holiday_cnt.png
休日と休日以外でこんなに違うのか？ と思うくらいcntの違いが確認できました。実データ(day.csv)を調べてみたら、2年間で休日が21日間しかなかったのでこんなものかと納得。

weekdayとcntの相関関係を可視化

weekdayとcntの相関関係を可視化
grouped = day_df[['cnt', 'yr', 'weekday']].groupby(['yr', 'weekday']).agg({'cnt':'sum'}).reset_index()
plt.figure(figsize=(10, 6))
sns.barplot(data=grouped, x='weekday', y='cnt', hue='yr', palette=['blue', 'green'])
plt.xlabel('weekday')
plt.ylabel('Sum of Value')
plt.title('Sum of Value by weekday')
plt.show()

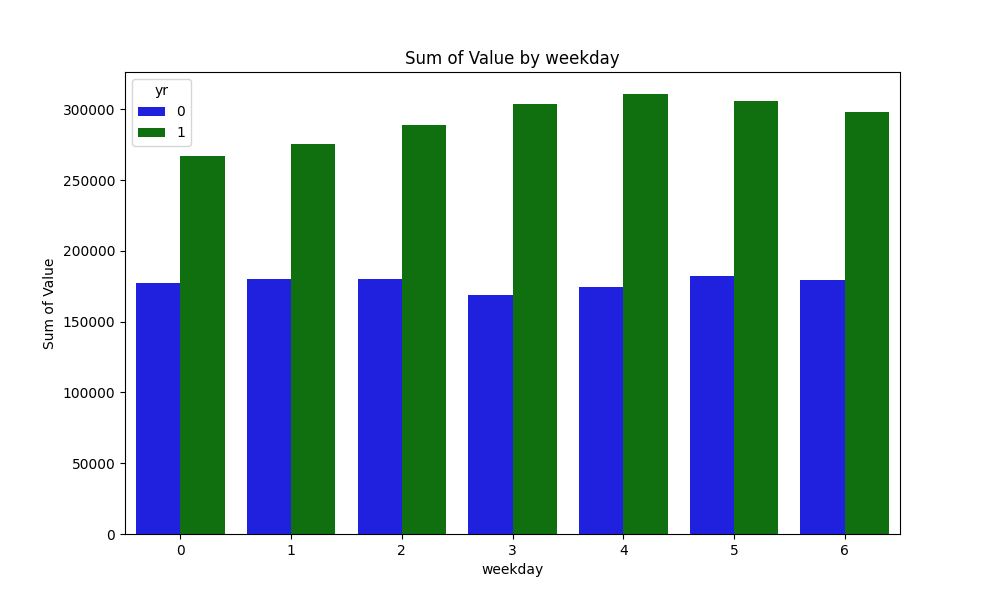
weekday_cnt.png
曜日のトレンドが2011年と2012年で少し異なっていることを確認。2011年は3(木)が最も少ない曜日なのに対して、2012年は0(月)が最も少ない曜日となっている。これまでの確認結果からも言えることだが訓練データとテストデータとして、年に偏ったデータを抽出してしまったらうまく予想ができないので注意が必要であることをメモする。

workingdayとcntの相関関係を可視化

workingdayとcntの相関関係を可視化
grouped = day_df[['cnt', 'yr', 'workingday']].groupby(['yr', 'workingday']).agg({'cnt':'sum'}).reset_index()
plt.figure(figsize=(10, 6))
sns.barplot(data=grouped, x='workingday', y='cnt', hue='yr', palette=['blue', 'green'])
plt.xlabel('workingday')
plt.ylabel('Sum of Value')
plt.title('Sum of Value by workingday')
plt.show()

working_cnt.png
土日祝日は0、それ以外は1。特に気になる点はない。

weathersitとcntの相関関係を可視化

weathersitとcntの相関関係を可視化
grouped = day_df[['cnt', 'yr', 'weathersit']].groupby(['yr', 'weathersit']).agg({'cnt':'sum'}).reset_index()
plt.figure(figsize=(10, 6))
sns.barplot(data=grouped, x='weathersit', y='cnt', hue='yr', palette=['blue', 'green'])
plt.xlabel('weathersit')
plt.ylabel('Sum of Value')
plt.title('Sum of Value by weathersit')
plt.show()

weathersit_cnt.png
3（小雪、小雨+雷雨+雲が散らばる、小雨+雲が散らばる）で2011年と2012年の件数が僅かだが逆転している。要因は天候にあると想定し問題はないと判断。

humとcntの相関関係を可視化

humとcntの相関関係を可視化
sns.regplot(data=day_df, x='hum', y='cnt')
plt.xlabel('hum')
plt.ylabel('cnt')
plt.title('hum vs cnt')
plt.show()

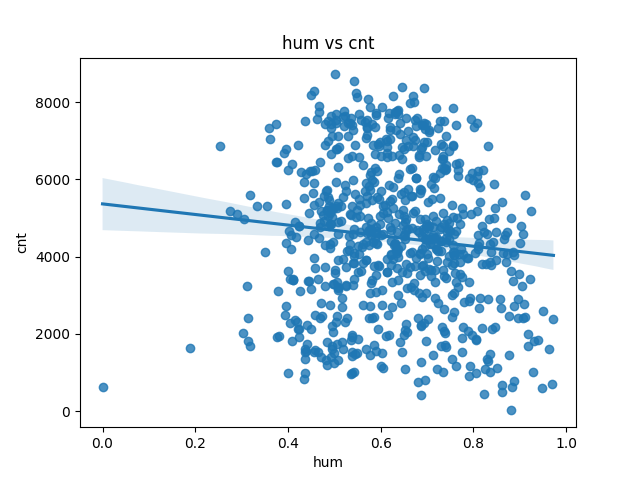
hum_cnt.png
humは湿度。このチャートを見た目だけでは相関を判断することはできない。因みに自分に当てはめて考えてみた場合、湿度で交通手段を変更することは考えられない。そもそも湿度を知る方法がない。よって湿度は他の特徴量の従属変数ではないかと予想。なお、先述のヒートマップでは weathersit（天候）と0.59の相関係数があることを再確認。

windspeedとcntの相関関係を可視化

windspeedとcntの相関関係を可視化
sns.regplot(data=day_df, x='windspeed', y='cnt')
plt.xlabel('windspeed')
plt.ylabel('cnt')
plt.title('windspeed vs cnt')
plt.show()

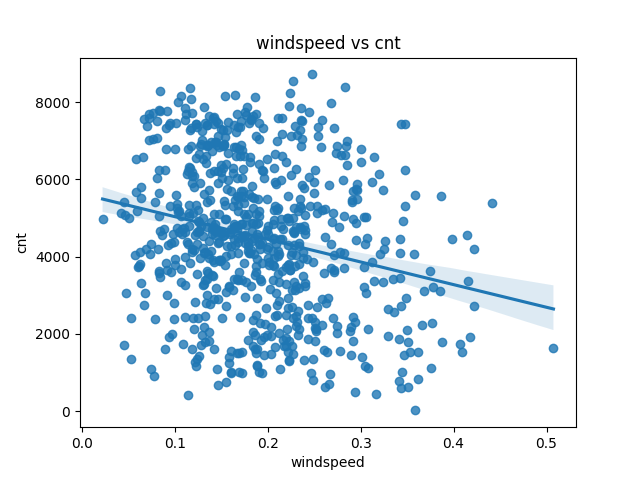
windspeed_cnt.png
windspeedは風速。こちらもこのチャートを見た目だけでは相関を判断することはできない。若干負の相関がありそうという程度。

データ理解のまとめ

・本データは731行×16行の日次のデータセット
・データは1レコードが1日分となっており、2021年1月1日から2022年12月31日まで2年分のデータが存在している。
・データ項目は１項目（日付文字列）以外すべて数値データ
・カテゴリ変数は7つ
・欠損値、Na値ともに無し。
・重複データは無し
・外れ値は全体で15件
・特徴量のtempとatempには99%以上の相関関係がある。
・ターゲットとなる件数データについて、2021年は全体的に2022年を下回っている。

３．データ準備

データ準備は以下の手順で実施することとする。

  1. 欠損値処理
  2. 重複値処理
  3. 外れ値処理
  4. ダミー変数化
  5. 特徴量作成
  6. 不要な特徴量を削除
  7. ターゲット設定
  8. 標準化
  9. テストデータ定義

３－１．欠損値処理

今回使用するデータには欠損値がないため本プロセスは省略します。

３－２．重複値処理

今回使用するデータには重複値がないため本プロセスは省略します。

３－３．外れ値処理

外れ値の確認で記載したように今回使用するデータには外れ値があります。
外れ値の対象が hum(湿度）とwindspeed（風速）となっており、実際に発生した気象情報と考えられるため、どのように対応すればよいか迷いましたが、その日の気象が異常であったと判断し、対象行をdrop（リストワイズ削除）する判断をしました。

外れ値の削除
#外れ値にマーキングの為Noneを設定する
def outlier_adj(df):
    
    for i in range(len(df.columns)):

        # 列を抽出する
        col = df.iloc[:,i]

        # 四分位数
        q1 = np.percentile(col, 25)
        q3 = np.percentile(col, 75)
        iqr = q3 - q1 #四分位範囲

        # 外れ値の基準点
        outlier_min = q1 - (iqr) * 1.5
        outlier_max = q3 + (iqr) * 1.5

        # 範囲から外れている値を除く
        col[col < outlier_min] = None
        col[col > outlier_max] = None

    return df

# 例外値にNoneを設定
day_df_tmp = outlier_adj(day_df.loc[:, ['temp','atemp','hum','windspeed']])

# None設定後のデータで書き換え
day_df['temp'] = day_df_tmp['temp']
day_df['atemp'] = day_df_tmp['atemp']
day_df['hum'] = day_df_tmp['hum']
day_df['windspeed'] = day_df_tmp['windspeed']

print('shape before:', day_df.shape)
# null行削除（リストワイズ削除）
day_df.dropna(inplace=True)
print('shape after:', day_df.shape)

>>> 出力結果
shape before: (731, 16)
shape after: (717, 16)

この対応の為、データ件数が731件から717件に変更となっています。

３－４．ダミー変数処理

7つのダミー変数を全てOne-Hot Encodingします。

ダミー変数のOne Hot Encoding
# カテゴリカル変数をOne-Hot Encoding
day_df = pd.get_dummies(day_df, columns= ['season', 'yr','mnth','holiday','weekday','workingday', 'weathersit'], dtype=float)

３－５．特徴量作成

tempとatempの相関が非常に高いため、1つの特徴量に纏めます。どちらかの変数を削除するでもよかったのですが、Copilot様よりPCAによる次元削除の方法を提案いただいたので、その方針で進めることとします。

PCAによる次元削除
df_tmp = day_df.loc[:, ['temp', 'atemp']]
pca = PCA(n_components=1)
pca.fit(df_tmp)
df_pca = pca.transform(df_tmp)

# 新しい特徴量 temp_newとして登録
day_df['temp_new'] = df_pca

tempとatempを一つの特徴量temp_newにまとめました。

３－６．不要な特徴量の削除

不要な特徴量の削除
# 学習に不要な特徴量を削除
drop_col = [ 'instant', 'temp', 'atemp', 'casual', 'registered' ]
day_df = day_df.drop(drop_col, axis=1)

３－７．ターゲット設定

ターゲット設定
# cntをターゲットに設定
df_target = pd.DataFrame( day_df['cnt'], columns=['cnt'] )

３－８．標準化

sklearn.preprocessing.StandardScalerを利用し、全ての特徴量を標準化する。

データ標準化
# 特徴量データからターゲットを削除
day_df = day_df.drop(['cnt'], axis=1)

# データ標準化(日付データは除く)
scaling_columns = day_df.columns[1:]

# StandardScaler を用いて全特徴量を標準化
sc = StandardScaler().fit(day_df[scaling_columns])
day_df_std = pd.DataFrame(sc.transform(day_df[scaling_columns]), columns=scaling_columns, index=day_df.index)

３－９．テストデータ定義

ランダムで抽出した全体の2割のデータをテストデータとして固定する。
random_stateに0を設定することでデータの再現性を担保する。

テストデータ定義
# 訓練データとテストデータを作成
# 以降、データの２割をテストデータとして固定
X_train, X_test, y_train, y_test = train_test_split(
    day_df_std, df_target, 
    test_size=0.2, shuffle=True, random_state=0
    )

４．モデリング

まず評価を開始する前に今回のモデリングの評価指標を決めました。
今回は回帰モデルなので決定係数 R2 を評価指標とし最大のR2を導出したモデルを最適なモデルと定義します。　なお、参考までに平均二乗誤差 MSE も同時に記録していきます。

評価のステップを以下の手順で行うこととします。

1.単独回帰モデルでの評価
2.バギング手法を用いた評価
3.ブースティング手法を用いた評価
4.スタッキング手法を用いた評価

４－１．単独回帰モデルでの評価

回帰に利用できるモデルを片っ端から使用してモデリングを行います。パラメーターにrandom_stateが設定できるモデルは必ず0を設定して再現性を担保します。
今回単独回帰モデルの評価としたのは以下のモデルになります。

  1. LinearRegression
  2. Ridge
  3. Lasso
  4. ElasticNet
  5. DecisionTreeRegressor
  6. RandomForestRegressor
  7. SVR
  8. KNeighborsClassifier
  9. LinearSVR
  10. BaggingRegressor
  11. AdaBoostRegressor
  12. LGBMRegressor
  13. MLPRegressor

この内、RandomForestRegressor、BaggingRegressor、AdaBoostRegressor、LGBMRegressorはバギングやブースティングといった手法に含まれますが、コーディングの表記上単独のモデルで実装できるので本評価の対象としました。該当のモデルについては後述のバギングやブースティングの中でも改めて評価を行うこととします。

以下にどのような評価を行ったのか、DecisionTreeRegressorを例にコードを提示します。実際のコードでは、この以下のコードのDecisionTreeRegressorにあたる部分を上記のモデル全てに対し実装して、最終的に評価指標が最大となったモデルを最適なモデルとして評価しています。

単独モデルの評価

# 評価指標 R2 （決定係数）
max_r2 = 0
best_model = None
best_model_mse = 0

# モデルの学習
model = DecisionTreeRegressor(random_state=0)

model.fit(X_train, y_train)
y_pred = model.predict(X_test)

# 決定係数(R2)
r2 = r2_score(y_test, y_pred)

# 平均二乗誤差(MSE)
mse = MSE(y_test, y_pred)

print("DecisionTreeRegressor R2 : %.3f" % r2)
print("DecisionTreeRegressor MSE : %.3f" % mse)

if(r2 > max_r2):
    max_r2 = r2
    best_model = 'DecisionTreeRegressor'
    best_model_mse = mse

# 次のモデルに続く

print(f'最適なモデルは{best_model}、決定係数は{max_r2:.3f}、平均二乗誤差は{best_model_mse:.3f}')

以下、出力結果です。チューニングしていないので、もっと伸びしろのあるモデルはあるかと思いますが、全部チューニングするのはコストがかかりすぎるので、まずは（ほぼ）デフォルトのパラメーターで良さげなモデルを選択し、そのモデルに対してチューニングを行く方針とします。

LinearRegression R2 : 0.879
LinearRegression MSE : 543795.790
Ridge R2 : 0.879
Ridge MSE : 543091.776
Lasso R2 : 0.879
Lasso MSE : 544665.101
ElasticNet R2 : 0.840
ElasticNet MSE : 720627.386
DecisionTreeRegressor R2 : 0.874
DecisionTreeRegressor MSE : 567971.556
RandomForestRegressor R2 : 0.925
RandomForestRegressor MSE : 334950.058
SVR R2 : 0.631
SVR MSE : 1658509.850
KNeighborsClassifier R2 : 0.027
KNeighborsClassifier MSE : 4374403.979
LinearSVR R2 : -3.659
LinearSVR MSE : 20943645.026
BaggingRegressor R2 : 0.921
BaggingRegressor MSE : 356045.997
AdaBoostRegressor R2 : 0.830
AdaBoostRegressor MSE : 762721.117
LGBMRegressor R2 : 0.911
LGBMRegressor MSE : 401736.172
MLPRegressor R2 : 0.793
MLPRegressor MSE : 931372.373
最適なモデルはRandomForestRegressor、決定係数は0.925、平均二乗誤差は334950.058

結果、最適モデルはRandomForestRegressor（ランダムフォレスト）となりました。R2（決定係数）が0.925とはなかなかの精度がでています。

中には、R2がマイナスのモデルがあったり、個人的に注目していたMLPRegressorが低評価になっていたり（どうしたディープラーニング！？）とひとつひとつ丁寧にチューニングを行っていきたいところですが今後の課題として残しておき、当初方針どおり最適モデルとなったRandomForestRegressor に対し更なるチューニングをしていきたいと思います。ちなみにRandomForestRegressorはバギングの手法の一つなので、次の「バギング手法を用いた評価」でも改めて評価対象とします。

４－２．バギング手法を用いた評価

前回は基本単独のモデルを使った評価を行いましたが、本項以降アンサンブル学習として複数のモデルを組み合わせて更なるモデルの精度向上を目指します。

今回実施するのはバギングを用いた評価です。バギングでは、同時に複数のモデルに学習させて、予測結果の平均をとることで汎化能力を向上させます。

今回バギングとして評価するにあたり、対象となる一番上位にあたるモデル2つを以下に示します。

  1. RandomForestRegressor
  2. BaggingRegressor

そして、今回よりパラメーターチューニングも実施しています。　パラメーターチューニングに用いたライブラリは optuma です。optumaについては内容の理解がまだまだ足りておらず、都度ネットで調べながら試行錯誤ですすめているような実情でございますので、何かお気づきの点がございましたら、ご教示いただけると幸いです。

バギング用に作成したコードは以下になります。

バギング
#
# モデリング （バギング）
#

# 評価指標 R2 （決定係数）
max_r2 = 0
best_model = None
best_model_mse = 0

# yを(n_samples, )の配列に変換
y_train=np.reshape(y_train,(-1))
y_test=np.reshape(y_test,(-1))

# optunaの目的関数を設定する
def objective(trial):
    criterion = trial.suggest_categorical('criterion', ['squared_error', 'poisson', 'absolute_error', 'friedman_mse'])
    bootstrap = trial.suggest_categorical('bootstrap', [True, False])
    max_depth = trial.suggest_int('max_depth', 1, 1000)
    max_features = trial.suggest_categorical('max_features', ['sqrt','log2'])
    max_leaf_nodes = trial.suggest_int('max_leaf_nodes', 2, 1000)
    n_estimators =  trial.suggest_int('n_estimators', 1, 1000)
    min_samples_split = trial.suggest_int('min_samples_split',2,5)
    min_samples_leaf = trial.suggest_int('min_samples_leaf',1,10)

    regr = RandomForestRegressor(criterion = criterion,
                                 bootstrap = bootstrap, 
                                 max_depth = max_depth, 
                                 max_features = max_features,
                                 max_leaf_nodes = max_leaf_nodes,
                                 n_estimators = n_estimators,
                                 min_samples_split = min_samples_split,
                                 min_samples_leaf = min_samples_leaf,
                                 n_jobs=2,
                                 random_state=0)

    score = cross_val_score(regr, X_train, y_train, cv=5, scoring="r2")
    r2_mean = score.mean()

    return r2_mean

# optunaで最適値を見つける
study = optuna.create_study(direction='maximize')
study.optimize(objective, n_trials=100)

# チューニングしたハイパーパラメーターをフィット
model = RandomForestRegressor(  criterion = study.best_params['criterion'],
                                bootstrap = study.best_params['bootstrap'], 
                                max_depth = study.best_params['max_depth'], 
                                max_features = study.best_params['max_features'],
                                max_leaf_nodes = study.best_params['max_leaf_nodes'],
                                n_estimators = study.best_params['n_estimators'],
                                min_samples_split = study.best_params['min_samples_split'],
                                min_samples_leaf = study.best_params['min_samples_leaf'],
                                n_jobs=2,
                                random_state=0)

model.fit(X_train, y_train)
y_pred = model.predict(X_test)

# 決定係数(R2)
r2 = r2_score(y_test, y_pred)

# 平均二乗誤差(MSE)
mse = MSE(y_test, y_pred)

print("RandomForestRegressor R2 : %.3f" % r2)
print("RandomForestRegressor MAE : %.3f" % mse)

if(r2 > max_r2):
    max_r2 = r2
    best_model = 'RandomForestRegressor'
    best_model_mse = mse

# モデルの学習
model = BaggingRegressor(
            DecisionTreeRegressor(random_state=0, max_depth=100),n_estimators=1000, random_state=0)

model.fit(X_train, y_train)
y_pred = model.predict(X_test)

# 決定係数(R2)
r2 = r2_score(y_test, y_pred)

# 平均二乗誤差(MSE)
mse = MSE(y_test, y_pred)

print("BaggingRegressor R2 : %.3f" % r2)
print("BaggingRegressor MSE : %.3f" % mse)

if(r2 > max_r2):
    max_r2 = r2
    best_model = 'BaggingRegressor'
    best_model_mse = mse

print(f'最適なモデルは{best_model}、決定係数は{max_r2:.3f}、平均二乗誤差は{best_model_mse:.3f}')

以下、出力結果です。

RandomForestRegressor R2 : 0.911
RandomForestRegressor MAE : 400100.416
BaggingRegressor R2 : 0.926
BaggingRegressor MSE : 331603.260
最適なモデルはBaggingRegressor、決定係数は0.926、平均二乗誤差は331603.260

バギング手法を用いた評価については、どちらも決定係数0.9を超えてきましたが、わずかな差でBaggingRegressorが最適モデルとなりました。 決定係数は0.926です。

この数値はチューニング実施前のRandomForestRegressorの決定係数0.925を僅か0.001ですが更新することが出来ました。

なお、RandomForestRegressorについてはチューニング前よりも評価が低くなってしまいました。チューニングパラメータに誤りがあるのか、学習数が少なかったのか、原因については今後の課題としておきます。

次のステップでは、低バリアンスと低バイアスに効果があるといわれている、ブースティング手法を用いた評価に進みまます。

４－３．ブースティング手法を用いた評価

ブースティングは、複数の弱学習器（通常は決定木など）を順番に学習させます。学習は順番に行われ、一度に一つの学習器が追加されます。前の学習器が正確な予測を行えば、その誤りに焦点を当てる新たな学習器が追加されます。

今回ブースティングとして評価するにあたり、対象となる一番上位にあたるモデル4つを以下に示します。これらを評価する際にチューニングも合わせて実施していきます。

  1. AdaBoostRegressor
  2. GradientBoostingRegressor
  3. XGBRegressor
  4. LGBMRegressor

なお、AdaBoostRegressorはBaggingRegressorと合わせ技で実施しています。弱学習機として、DecisionTreeRegressorとKNeighborsRegressorの2つのモデルを選択したパターンで評価していきます。

ブースティング用に作成したコードは以下になります。

ブースティング
#
# モデリング （ブースティング）
#

# 評価指標 R2 （決定係数）
max_r2 = 0
best_model = None
best_model_mse = 0

# yを(n_samples, )の配列に変換
y_train=np.reshape(y_train,(-1))
y_test=np.reshape(y_test,(-1))

#
# AdaBoostRegressor
# 

# モデルの学習（DecisionTreeRegressor）
model = AdaBoostRegressor(
            BaggingRegressor(
                DecisionTreeRegressor(),
            n_estimators=100,
            random_state=0),
        n_estimators=100,
        random_state=0)

model.fit(X_train, y_train)
y_pred = model.predict(X_test)

# 決定係数(R2)
r2 = r2_score(y_test, y_pred)

# 平均二乗誤差(MSE)
mse = MSE(y_test, y_pred)

print("AdaBoostRegressor & DecisionTreeRegressor R2 : %.3f" % r2)
print("AdaBoostRegressor & DecisionTreeRegressor MSE : %.3f" % mse)

if(r2 > max_r2):
    max_r2 = r2
    best_model = 'AdaBoostRegressor & DecisionTreeRegressor'
    best_model_mse = mse


# モデルの学習（KNeighborsRegressor）
model = AdaBoostRegressor(
            BaggingRegressor(
                KNeighborsRegressor(),
            n_estimators=100,
            random_state=0),
        n_estimators=100,
        random_state=0)

model.fit(X_train, y_train)
y_pred = model.predict(X_test)


# 決定係数(R2)
r2 = r2_score(y_test, y_pred)

# 平均二乗誤差(MSE)
mse = MSE(y_test, y_pred)

print("AdaBoostRegressor & KNeighborsRegressor R2 : %.3f" % r2)
print("AdaBoostRegressor & KNeighborsRegressor MSE : %.3f" % mse)

if(r2 > max_r2):
    max_r2 = r2
    best_model = 'AdaBoostRegressor & KNeighborsRegressor'
    best_model_mse = mse

#
# GradientBoostingRegressor
#

def objective(trial):

    #評価するハイパーパラメータの値を規定
    params ={
        'n_estimators':trial.suggest_int('n_estimators', 3, 30),
        'min_samples_split':trial.suggest_int('min_samples_split',2,20),
        'min_samples_leaf':trial.suggest_int('min_samples_leaf',1,100),
        'max_depth':trial.suggest_int('max_depth', 1, 20),
        'max_features':trial.suggest_categorical('max_features', ['sqrt', 'log2']),
        'loss':trial.suggest_categorical('loss', ['squared_error', 'absolute_error', 'huber', 'quantile']),
        'subsample':trial.suggest_uniform('subsample',0.5,1.0)
    }

    model = GradientBoostingRegressor(
                            **params,
                            random_state=0)

    #交差検証
    score = cross_val_score(model, X_train, y_train, cv=5, scoring="r2")
    r2_mean = score.mean()

    return r2_mean

#optuna.create_study()でoptuna.studyインスタンスを作る。
study = optuna.create_study(direction='maximize')
study.optimize(objective, n_trials=100)

model = GradientBoostingRegressor(
                n_estimators =study.best_params['n_estimators'],
                min_samples_split=study.best_params['min_samples_split'],
                min_samples_leaf=study.best_params['min_samples_leaf'],
                max_depth=study.best_params['max_depth'],
                max_features=study.best_params['max_features'],
                loss=study.best_params['loss'],
                subsample=study.best_params['subsample'],
                random_state=0
            )   

model.fit(X_train, y_train)
y_pred = model.predict(X_test)

# 決定係数(R2)
r2 = r2_score(y_test, y_pred)

# 平均二乗誤差(MSE)
mse = MSE(y_test, y_pred)

print("GradientBoostingRegressor R2 : %.3f" % r2)
print("GradientBoostingRegressor MSE : %.3f" % mse)

if(r2 > max_r2):
    max_r2 = r2
    best_model = 'GradientBoostingRegressor'
    best_model_mse = mse

#
# XGBRegressor
#

def objective(trial, df_X, df_y):

    #評価するハイパーパラメータの値を規定
    params ={
        'max_depth':trial.suggest_int("max_depth", 1, 20),
        'min_child_weight':trial.suggest_int('min_child_weight',1,5),
        'gamma':trial.suggest_uniform('gamma',0,1),
        'subsample':trial.suggest_uniform('subsample',0,1),
        'colsample_bytree':trial.suggest_uniform('colsample_bytree',0,1),
        'reg_alpha':trial.suggest_loguniform('reg_alpha',1e-5,100),
        'reg_lambda':trial.suggest_loguniform('reg_lambda',1e-5,100),        
        'learning_rate':trial.suggest_uniform('learning_rate',0,1)
    }

    model = xgb.XGBRegressor(
                            n_estimators=100,
                            verbosity=0,
                            n_jobs=-1,
                            random_state=0,
                            **params)

    #交差検証
    scores = cross_val_score(model, df_X, df_y, scoring="r2", cv=5)
    r2_mean = scores.mean()

    return r2_mean

#optuna.create_study()でoptuna.studyインスタンスを作る。
study = optuna.create_study(direction='maximize')

#studyインスタンスのoptimize()に作った関数を渡して最適化する。
study.optimize(lambda trial: objective(trial, X_train, y_train), n_trials=100)

model = xgb.XGBRegressor(
                # objective='reg:squaredlogerror',
                _estimators=100,
                verbosity=0,
                n_jobs=-1,
                random_state=0,
                max_depth=study.best_params['max_depth'],
                min_child_weight=study.best_params['min_child_weight'],
                gamma=study.best_params['gamma'],
                subsample=study.best_params['subsample'],
                colsample_bytree=study.best_params['colsample_bytree'],
                reg_alpha=study.best_params['reg_alpha'],
                reg_lambda=study.best_params['reg_lambda'],
                learning_rate=study.best_params['learning_rate']
            )   

model.fit(X_train, y_train)
y_pred = model.predict(X_test)

# 決定係数(R2)
r2 = r2_score(y_test, y_pred)

# 平均二乗誤差(MSE)
mse = MSE(y_test, y_pred)

print("XGBRegressor R2 : %.3f" % r2)
print("XGBRegressor MSE : %.3f" % mse)

if(r2 > max_r2):
    max_r2 = r2
    best_model = 'XGBRegressor'
    best_model_mse = mse

#
# LGBMRegressor
#

# optunaの目的関数を設定する
def objective(trial):

    param = {
        'boosting_type':'gbdt',
        'objective':'regression',
        'metric':'mea',
        'max_depth': trial.suggest_int('max_depth', 1, 20),
        'lambda_l1': trial.suggest_loguniform('lambda_l1', 1e-8, 10.0),
        'lambda_l2': trial.suggest_loguniform('lambda_l2', 1e-8, 10.0),
        'num_leaves': trial.suggest_int('num_leaves', 2, 256),
        'feature_fraction': trial.suggest_uniform('feature_fraction', 0.4, 1.0),
        'bagging_fraction': trial.suggest_uniform('bagging_fraction', 0.4, 1.0),
        'bagging_freq': trial.suggest_int('bagging_freq', 1, 7),
        'min_child_samples': trial.suggest_int('min_child_samples', 5, 100),
        'min_data_in_leaf': trial.suggest_int('min_data_in_leaf', 5, 100),
        'random_state':'1'
    }

    model = lgb.LGBMRegressor(**param)

    # クロスバリデーション検証 (5分割)
    score = cross_val_score(model, X_train, y_train, cv=5, scoring="r2")
    r2_mean = score.mean()

    return r2_mean

# optunaで最適値を見つける
study = optuna.create_study(direction='maximize')
study.optimize(objective, n_trials=100)

# チューニングしたハイパーパラメーターをフィット
model = lgb.LGBMRegressor(
                objective='regression', 
                metric='mea', 
                random_state=0,
                max_depth=study.best_params['max_depth'],
                lambda_l1=study.best_params['lambda_l1'],
                lambda_l2=study.best_params['lambda_l2'],
                num_leaves=study.best_params['num_leaves'],
                feature_fraction=study.best_params['feature_fraction'],
                bagging_fraction=study.best_params['bagging_fraction'],
                bagging_freq=study.best_params['bagging_freq'],
                min_child_samples=study.best_params['min_child_samples'],
                min_data_in_leaf=study.best_params['min_data_in_leaf']
            )   

model.fit(X_train, y_train)
y_pred = model.predict(X_test)

# 決定係数(R2)
r2 = r2_score(y_test, y_pred)

# 平均二乗誤差(MSE)
mse = MSE(y_test, y_pred)

print("LGBMRegressor R2 : %.3f" % r2)
print("LGBMRegressor MSE : %.3f" % mse)

if(r2 > max_r2):
    max_r2 = r2
    best_model = 'LGBMRegressor'
    best_model_mse = mse

print(f'最適なモデルは{best_model}、決定係数は{max_r2:.3f}、平均二乗誤差は{best_model_mse:.3f}')

以下、出力結果です。

AdaBoostRegressor & DecisionTreeRegressor R2 : 0.922
AdaBoostRegressor & DecisionTreeRegressor MSE : 351764.524
AdaBoostRegressor & KNeighborsRegressor R2 : 0.790
AdaBoostRegressor & KNeighborsRegressor MSE : 945259.939
GradientBoostingRegressor R2 : 0.914
GradientBoostingRegressor MSE : 384720.914
XGBRegressor R2 : 0.927
XGBRegressor MSE : 328675.229
LGBMRegressor R2 : 0.928
LGBMRegressor MSE : 321591.007
最適なモデルはLGBMRegressor、決定係数は0.928、平均二乗誤差は321591.007

最適なモデルはLGBMRegressor、決定係数は0.928、平均二乗誤差は321591.007 となりこれまでの最高値0.926を0.002ポイント更新しました！ わずかではありますが、これはうれしい！

４－４．スタッキング手法を用いた評価

スタッキングでは、複数の異なるモデル（例えば、決定木、サポートベクトルマシン、ニューラルネットワークなど）が同時に学習されます。個々のモデルの予測を元に、それらを組み合わせて新たなモデルを学習させます。ということですが、さっそくやっていきたいと思います。

第一層のモデルには、単独回帰モデルでの評価でつかった以下の複数のモデルを設定します。

  1. LinearRegression
  2. Ridge
  3. Lasso
  4. ElasticNet
  5. DecisionTreeRegressor
  6. RandomForestRegressor
  7. SVR
  8. LinearSVR
  9. BaggingRegressor
  10. AdaBoostRegressor
  11. lgb.LGBMRegressor
  12. MLPRegressor
  13. GradientBoostingRegressor

最終層で実行するXGBRegressorは事前にパラメータチューニングを実施しています。
また、vecstackを使った手法と、StackingTransformerを使ってsklearnのPipelineに連携する方法の2つの手順で実装しています。

スタッキング
#
# モデリング （スタッキング）
#

# 評価指標 R2 （決定係数）
max_r2 = 0
best_model = None
best_model_mse = 0

# yを(n_samples, )の配列に変換
y_train=np.reshape(y_train,(-1))
y_test=np.reshape(y_test,(-1))


# パラメータチューニング
def objective(trial, df_X, df_y):

    #評価するハイパーパラメータの値を規定
    params ={
        'max_depth':trial.suggest_int("max_depth",1,100),
        'min_child_weight':trial.suggest_int('min_child_weight',1,5),
        'gamma':trial.suggest_uniform('gamma',0,1),
        'subsample':trial.suggest_uniform('subsample',0,1),
        'colsample_bytree':trial.suggest_uniform('colsample_bytree',0,1),
        'reg_alpha':trial.suggest_loguniform('reg_alpha',1e-5,100),
        'reg_lambda':trial.suggest_loguniform('reg_lambda',1e-5,100),        
        'learning_rate':trial.suggest_uniform('learning_rate',0,1)
    }

    model = xgb.XGBRegressor(
                            n_estimators=100,
                            verbosity=0,
                            n_jobs=-1,
                            random_state=0,
                            **params)

    #交差検証
    scores = cross_val_score(model, df_X, df_y, scoring="r2", cv=5)
    r2_mean = scores.mean()
    print(r2_mean)

    return r2_mean

# あらかじめXGBRegressorをチューニング
study = optuna.create_study(direction='maximize')
study.optimize(lambda trial: objective(trial, X_train, y_train), n_trials=100)

# スタッキング一層目
models = [
        LinearRegression(),
        Ridge(random_state=0),
        Lasso(random_state=0),
        ElasticNet(random_state=0),
        DecisionTreeRegressor(random_state=0),
        RandomForestRegressor(random_state=0),
        SVR(),
        KNeighborsRegressor(),
        LinearSVR(random_state=0),
        BaggingRegressor(random_state=0),
        AdaBoostRegressor(random_state=0),
        lgb.LGBMRegressor(random_state=0, force_row_wise=True),
        MLPRegressor(random_state=0),
        GradientBoostingRegressor(random_state=0)
        ]

S_train, S_test = stacking(models,
        X_train, y_train, X_test,
        regression=True,                
        mode='oof_pred_bag',
        needs_proba=False,
        save_dir=None,
        metric=MSE,
        n_folds=5,
        shuffle=True,
        random_state=0
        # verbose=2
        )

model = xgb.XGBRegressor(
                # objective='reg:squaredlogerror',
                _estimators=100,
                verbosity=0,
                n_jobs=-1,
                random_state=0,
                max_depth=study.best_params['max_depth'],
                min_child_weight=study.best_params['min_child_weight'],
                gamma=study.best_params['gamma'],
                subsample=study.best_params['subsample'],
                colsample_bytree=study.best_params['colsample_bytree'],
                reg_alpha=study.best_params['reg_alpha'],
                reg_lambda=study.best_params['reg_lambda'],
                learning_rate=study.best_params['learning_rate']
            )   

model = model.fit(S_train, y_train)
y_pred = model.predict(S_test)

# 評価
# 決定係数(R2)
r2 = r2_score(y_test, y_pred)

# 平均二乗誤差(MSE)
mse = MSE(y_test, y_pred)

print("Stacking XGBRegressor R2 : %.3f" % r2)
print("Stacking XGBRegressor R2 MSE : %.3f" % mse)

if(r2 > max_r2):
    max_r2 = r2
    best_model = 'Stacking XGBRegressor'
    best_model_mse = mse

# スタッキング1層目
estimators_L1  = [
        ('lr', LinearRegression()),
        ('rg', Ridge(random_state=0)),
        ('ls', Lasso(random_state=0)),
        ('en', ElasticNet(random_state=0)),        
        ('dt', DecisionTreeRegressor(random_state=0)),
        ('rfr', RandomForestRegressor(random_state=0)),
        ('svr', SVR()),
        ('lsvr', LinearSVR(random_state=0)),
        ('br', BaggingRegressor(random_state=0)),
        ('abr', AdaBoostRegressor(random_state=0)),
        ('lgb', lgb.LGBMRegressor(random_state=0, force_row_wise=True)),
        ('mlp', MLPRegressor(random_state=0)),
        ('gbr', GradientBoostingRegressor(random_state=0))
        ]

stack = StackingTransformer(estimators=estimators_L1,
                            regression=True,
                            variant='A', 
                            metric=MSE,
                            n_folds=5,
                            shuffle=True,
                            random_state=0)

final_estimator  = xgb.XGBRegressor(
                _estimators=100,
                verbosity=0,
                n_jobs=-1,
                random_state=0,
                max_depth=study.best_params['max_depth'],
                min_child_weight=study.best_params['min_child_weight'],
                gamma=study.best_params['gamma'],
                subsample=study.best_params['subsample'],
                colsample_bytree=study.best_params['colsample_bytree'],
                reg_alpha=study.best_params['reg_alpha'],
                reg_lambda=study.best_params['reg_lambda'],
                learning_rate=study.best_params['learning_rate']
            )   

steps = [('stack', stack),
         ('final_estimator', final_estimator)]

# パイプラインの実行
pipe = Pipeline(steps)
pipe = pipe.fit(X_train, y_train)

y_pred = pipe.predict(X_test)

# 評価
# 決定係数(R2)
r2 = r2_score(y_test, y_pred)

# 平均二乗誤差(MSE)
mse = MSE(y_test, y_pred)

print("Stacking XGBRegressor Pipeline R2 : %.3f" % r2)
print("Stacking XGBRegressor Pipeline MSE : %.3f" % mse)

if(r2 > max_r2):
    max_r2 = r2
    best_model = 'Stacking XGBRegressor Pipeline'
    best_model_mse = mse

print(f'最適なモデルは{best_model}、決定係数は{max_r2:.3f}、平均二乗誤差は{best_model_mse:.3f}')

以下出力結果です。

Stacking XGBRegressor R2 : 0.927
Stacking XGBRegressor R2 MSE : 328685.371
Stacking XGBRegressor Pipeline R2 : 0.921
Stacking XGBRegressor Pipeline MSE : 355411.666
最適なモデルはStacking XGBRegressor、決定係数は0.927、平均二乗誤差は328685.371

最適なモデルはStacking XGBRegressor（sklearnとの連携無し）、決定係数は0.927、平均二乗誤差は328685.371となりました。

これまでの最大決定係数0.928には僅かに届きませんでしたが。うまくモデルを組み合わせたり、チューニングの最適化を行えば、もっと精度が出せる可能性を感じさせてくれました。

５．評価

今回は、モデリングフェーズで評価をしながらモデリングを構築してきました。
結果、モデリングを通して、最適と思われるモデルはブースティング手法のLGBMRegressorモデルとなりました。
その時の決定係数R2は 0.928、平均二乗誤差は321591.007です。これはまずまずの数字ではないかと思います。
また、実際に作業してみて、分析にあたりどこまでやればOKとするのか基準を最初に決めておくのも重要になるのではないかと感じました。 基準がないと永遠に分析を続けることが出来てしまうので。。

今後の学習課題とまとめ

本稿ではCRISP-DMプロセスに倣い実践をイメージしながら、教師あり学習、回帰モデルのデータ検証を行ったプロセスを共有させていただきました。 実際に手を動かすと数々の課題が発生し、その度に自分の学習ノート、同じ機械学習を学んでいる方々のブログ、およびChatGPT様（ときどきCopilot様）の力をかりつつどうにか最後まで纏めることができました。

データ分析に関して、今回は、初っ端からデータ選定に誤りがあることがわかり、想定していた件数よりも少ないデータを扱う行うこととなりました。次回は大量のデータ件数、大量の特徴量を持ったデーソースでの本格的なEDA作業にチャレンジしたいと思っています。

これまでの学習の振り返りとして、アウトプットする中でpandasやmatplotlib、seaborn等の基本的なライブラリの使い方がまだまだ定着していないことを実感しました。今後は定期的に学習した内容をブログを発信していく、Kaggleのコンペティションに参加する等できるだけアプトプットに力を入れて、いつかChatGPT様の借りずともコードを書けるよう、学んできたことを何度も反芻しながら、知識の定着を図っていきたいと考えています。

今後の学習目標について、今回少しだけ触れたパラメータチューニング、アンサンブル学習、そしてディープラーニングついてはまだまだ聞きかじった程度の状態なので、こちらは実践経験を積んで自分の血や肉になる程使いこなせるようになり、いつかKaggleのコンペティションでも上位に食い込めるようになりたいです！
最後に、Pythonを使ってやりたいことは画像認識や自然言語処理等他、山ほどあります。知識の定着と新しい学びのバランスをとりながら、あせらず、急がば回れの精神で今後も生涯学習を続けていければと思います。

最後までお付き合いいただき、有難うございました。

引用先リンク

今回のコードを書くにあたって特に参考にさせていただいたサイトを掲載いたします。

スタッキング手法については https://kagglenote.com/kaggle/stacking-by-vecstack/ を参照

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?