この記事は、Supershipグループ Advent Calendar 2020の17日目の記事になります。
楕円曲線に関する入門的なこと、楕円曲線暗号の仕組みについて(できるだけ)前提知識の必要がない解説をしたいと思います。
自己紹介
経歴的には数学をやっていました(2017年博士取得)。
普段の業務は広告・マーケティング領域で、広告セグメントの作成や研究開発をしています。
なお、この記事の作者は楕円曲線論は社会人になってから勉強しました。岩波の数論1とその他記事を読んだ程度の知識ですので間違いがあるかもしれません。
その際はご指摘下さいますと嬉しく存じます。
概要
楕円曲線とは大ざっぱに言うと、"とても性質の良い曲線"のことです。
なお、楕円という名前は付いていますがこの曲線は楕円ではありません。
楕円の由来は三角関数のような周期性を持つ関数(楕円関数という)でパラメトライズされる曲線なので楕円曲線という説明が一番私はしっくりきました。
楕円積分から来ているなど色々聞いたことがありますが正しい歴史は不明です。
本稿では楕円曲線の定義、例、その諸性質を述べ、その後楕円曲線が如何にして暗号理論に応用されているかを解説します。
楕円曲線暗号はRSA暗号などと同じ仕組みで公開鍵と秘密鍵を持つ暗号です。
僕が学生の頃(8~9年前)に暗号理論の専門家の方と話した際に楕円曲線暗号はPlay Stationに使われているという話を聞きました。
最近ではBitCoinに使われているということを聞きましたが、楕円曲線理論という数論的な研究対象が社会貢献できるんだと思った記憶があります。
ちなみに楕円曲線理論はあの有名なフェルマーの最終定理の解決に貢献した純粋数学的にも非常に面白い研究対象で、現在も活発に研究が行われています。
保型形式と楕円曲線が対応するという谷山志村予想の部分的な解決を通じてフェルマーの最終定理が示されたのですが、そのへんの話も面白いので、興味がある方はサイモン・シンの「フェルマーの最終定理」という本がおすすめです。
あと保型形式に関しては去年こんな記事を書いています。
楕円曲線
以下からは数学の話をします。
楕円曲線の定義を述べます。楕円曲線とは
y^2 = ax^3 + bx^2 + cx + d \quad (a,b,c,d \in \mathbb{Q}, a\neq 0)
であり右辺の3次式は重根を持たないという条件で与えられる曲線です。
ここで $\mathbb{Q}$ は有理数からなる集合とします。
楕円曲線の例は以下のような曲線です。
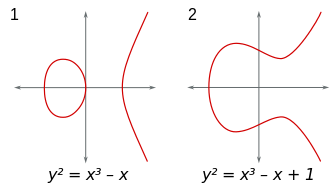
(図はWikipediaから引用)
左辺はただの$y^2$なのでx軸に関して上下対称となることはすぐにわかると思います。
( $(x,y)$ が楕円曲線の条件を満たせば $(x, -y)$ も満たすため)
さて、我々が知りたい対象はこの方程式の整数解や有理数解です。
一般に整数解は必ず有限個になることが示されています(Mordel, Siegel)。
しかし、有理数解は無限個にも有限個にもなり得ることが知られています(Mordel)。
なぜこれらの解が重要なのかということは以下の命題が良い例だと思われます。
命題1: $x^4 + y^4 = z^4$を満たす自然数解は存在しない。
これはフェルマーの最終定理の $n=4$ の場合ですが、実はこの証明は楕円曲線に関する以下の命題から容易に示されます。
命題2: $y^2 = x^3 -x$ の有理数解は $(0,0),\ (\pm1, 0)$ のみである。
命題1が命題2から従うことの証明:
背理法を用いる。 $x^4 + y^4 = z^4$ を満たす自然数解が存在するとする。
$y^4$ を移項して $z^2y^{-6}$ を掛けることにより
\left( \frac{x^2z}{y^3} \right)^2 = \left( \frac{z^2}{y^2} \right)^3 - \frac{z^2}{y^2}
と変形でき、これは命題2において $y\neq 0$ となる解を与えるので矛盾。
よって $x^4 + y^4 = z^4$ を満たす自然数解は存在しない。 [証明終]
このように楕円曲線から色々な不定方程式の整数解の存在を確かめることができます。
他にも合同数問題や素朴だが難しい問題に楕円曲線が活躍します。
楕円曲線上の点の足し算引き
楕円曲線$E$上の有理数解の集合に"無限遠点" $O$ を足したものを $E(\mathbb{Q})$ とします。
この"無限遠点" $O$ は全く新しい別の1点を付け加えていて原点と異なることに注意して下さい。
無限遠点ってなんやねんと思われるかもしれませんが、一点なんかそういう点があるんやなで大丈夫です。
これから順を追って雰囲気を解説していきます。
さて、この節ではこの集合$E(\mathbb{Q})$上に足し算引き算という演算が定まることを見ていきます。(この演算が楕円曲線暗号に使われます)
$E(\mathbb{Q})$ の点 $P, Q$ について、 $P+Q$ という新しい足し算をこれから以下のルールに従い定義します。
- 任意の点 $P \in E(\mathbb{Q})$ について $P+O = O + P = P$
- $P, Q \in E(\mathbb{Q})$, $P \neq O$, $Q \neq O$ の時、 $P,Q$ を通る直線を引き、その直線と楕円曲線 $E$ との交点を出し、その点を $x$ 軸に関して対称にした点を $P+Q$ とする。
- $P \in E(\mathbb{Q})$, $P \neq O$ の時、 $P = (x,y)$ とすると $-P = (x, -y)$ である。
なんのこっちゃですが、
1に関しては「ほーん、そういうルールなんやな」で良いと思います。
2に関しては「 $P$ と $Q$ を通る線を引いて交わる点を上下ひっくり返す」という図で見たら簡単なことをしています。
3に関しては「マイナス1倍ってのはひっくり返した点のことなんやな」で良いです。
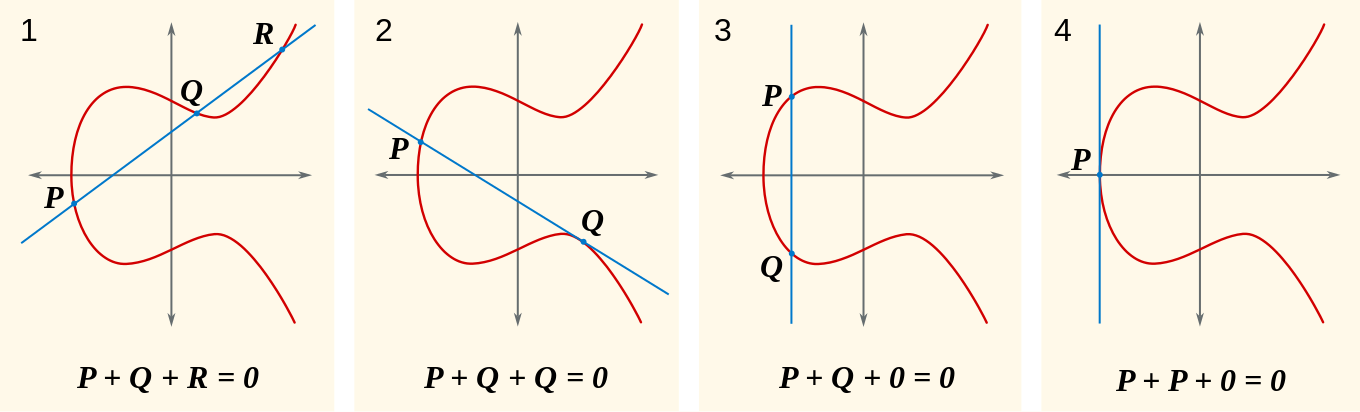
(図はwikipediaから引用)
なお、2の条件で $P=Q$ の場合は $P,Q$ を通る直線を $P$ に関する接線に関して同様の操作を行うとします。
注意: 点 $O$ に関する捕捉。
$P-P=O$ という計算を上記の3番目の図で理解しようとしたとします。
この場合は点を結ぶ直線と楕円曲線の交点が存在しないため、無限まで遠いところで交わっている感じで感覚的に理解されます。
また4番目の図も同様で、 $P$ から接線を引いていますが、交わる点がないため仮想的に無限遠点で交わっていると定義されていることが納得できます。
ここは後の小節で計算例を例示する際にもまた改めて解説します。
今後のために足し算の結果の点をexplicitに書いておきます。
$P = (x_1, y_1)$, $Q=(x_2, y_2)$ とする時、 $P+Q = (x_3, y_3)$ とし、この点を求める。
$x_1 \neq x_2$ の場合:
\begin{eqnarray}
x_3 &=& \frac{1}{a} \left( \frac{y_2-y_1}{x_2-x_1} \right)^2 - \frac{b}{a} -x_1 - x_2 \\\
y_3 &=& - \left( \frac{y_2-y_1}{x_2-x_1} \right) x_3 + \frac{y_2x_1-y_1x_2}{x_2-x_1}
\end{eqnarray}
$x_1 =x_2$ かつ $y_1 = -y_2$ の場合:
$P+Q = O$と定義する。
$x_1 =x_2$ かつ $y_1 \neq -y_2$ の時( $P=Q$ かつ $y_1 \neq 0$ と同値)の場合:
\begin{eqnarray}
x_3 &=& \frac{1}{4ay_1^2}(a^2 x_1^4 - 2acx_1^2 - 8adx_1 + c^2 - 4bd) \\\
y_3 &=& \frac{1}{8ay_1^3}{a^3x_1^6 + 2a^2bx_1^5 + 5a^2cx_1^4 + 20a^2dx_1^3 \\\
+ (20abd - 5ac^2)x_1^2 + (8b^2d-2bc^2 - 4acd)x_1 + (4bcd - 8ad^2 -c^3)}
\end{eqnarray}
となります。([数論I, 加藤黒川斎藤, 岩波書店]を参照しました)。
さて、楕円曲線上の演算に関して定義を行いましたが実は以下の偉大な定理があります。
定理 [Mordel, Weil]. $E$を$\mathbb{Q}$上の楕円曲線とすると$E(\mathbb{Q})$は有限生成アーベル群となる。
もう少し分かりやすく言うと、
「どんな楕円曲線 $E$ に対しても、$E$上に有限個の有理点 $P_1, P_2 , \ldots, P_n$ が存在して、全ての $E$ 上の有理点は $P_i$ の線形和で表す事ができる」
ということになります。有限個の点を足したり引いたりしまくったら全ての点が出てくると捉えて頂ければ大丈夫です。
上記の定理の証明はできないことはないのですが、かなり長くなるので割愛します(大体の楕円曲線に関する本には証明が載っていると思います)。
以上の定理より一般的な楕円曲線の代数構造自体は既に分かっていることになります(すごい!)
楕円曲線のpythonによる実装
以上のことを踏まえてpythonで実装していきます。
今回は適当に楕円曲線のクラスを作ってみました。
無限遠点 $O$ はグラフ上の点ではないことを表したかったので数値 $0$ として実装しています。
なんだか激しい計算をしていますが、仕方ないですね。
from fractions import Fraction
class EllipticCurve():
def __init__(self, a, b, c, d):
if a == 0:
raise ValueError("a=0 is forbidden!")
self.a = a
self.b = b
self.c = c
self.d = d
def isin(self, p):
if p == 0:
return True
x, y = p[0], p[1]
value = y**2 - self.a * (x ** 3) - self.b * (x**2) - self.c * x - self.d
if value == 0:
return True
return False
def sum(self, p, q):
if not self.isin(p):
raise ValueError("{} is not in the elliptic curve".format(p))
if not self.isin(q):
raise ValueError("{} is not in the elliptic curve".format(q))
if p == 0:
return q
if q == 0:
return p
x1, y1 = p[0], p[1]
x2, y2 = q[0], q[1]
if x1 != x2:
x3 = Fraction(1, self.a) * Fraction(y2-y1, x2-x1) ** 2 - Fraction(self.b , self.a) - x1 - x2
y3 = Fraction(y2-y1, x2-x1) * -x3 + Fraction(y2*x1 - y1*x2, x2 - x1)
return (x3, y3)
if x1 == x2 and y1 == -1 * y2:
return 0
if x1 == x2 and y1 != -1 * y2:
x3 = (Fraction(1, 4 * self.a * y1 ** 2)) *\
(self.a ** 2 * x1 **4 - 2 * self.a * self.c * x1 ** 2\
- 8* self.a * self.d * x1 - 4 * self.b * self.d)
y3 = Fraction(1, 8 * self.a * y1 ** 3) *\
(self.a ** 3 * x1 ** 6 + 2 * self.a **2 * self.b * x1 ** 5\
+ 5 * self.a**2 * self.c * x1 ** 4 + 20 * self.a ** 2 * self.d * x1 ** 3\
+ (20 * self.a * self.b * self.d - 5 * self.a * self.c **2) * x1**2\
+ (8 * self.b**2 * self.d - 2 * self.b * self.c**2 - 4 * self.a * self.c * self.d) * x1\
+ (4 * self.b * self.c * self.d - 8 * self.a * self.d**2 - self.c**3)
)
return (x3, y3)
以上のクラスを用いて少し実験をしてみましょう。
まずは以下の楕円曲線を考えます。
y^2 = x^3 + 1
$P = (2,3)$ はこの楕円曲線上の点を満たすので $P$ を足しまくってみましょう。
ell = EllipticCurve(1,0,0,1)
p = (2,3)
print(ell.isin(p))
p2 = ell.sum(p,p)
p3 = ell.sum(p2,p)
p4 = ell.sum(p3,p)
p5 = ell.sum(p4,p)
p6 = ell.sum(p5,p)
p7 = ell.sum(p6,p)
適当にプリントして結果をまとめます。
\begin{eqnarray}
P &=& (2,3)\\
2P &=& (0,1)\\
3P &=& (-1,0)\\
4P &=& (0,-1)\\
5P &=& (2,-3)\\
6P &=& O
\end{eqnarray}
おや、 $6P=O$ となりました。 $P + O = P$のため、これ以降は循環することになります。
図でまとめると以下の感じになります。
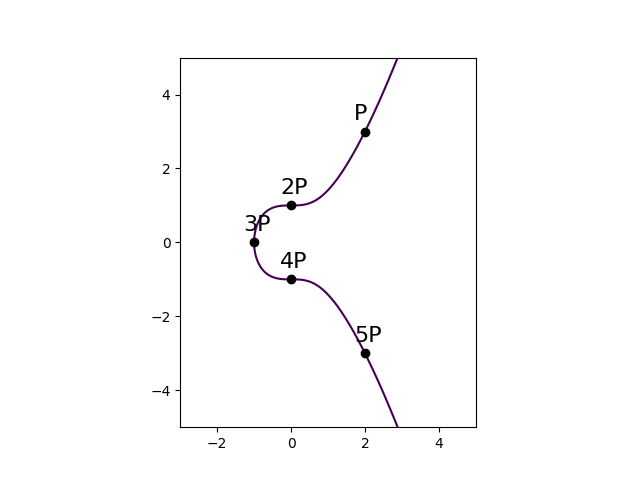
計算結果と図を見て再度考察をしていきます。
$2P + 4P = O$ ですが、定義から $2P$, $4P$を繋ぐ直線を引くとこれはまっすぐ縦に伸びる直線になります。
縦に伸びる直線は楕円曲線と交点を持たないため、仮想的に無限遠点を追加して無限遠点で交わるという感じになります。
無限遠点は一つなので上に伸びた直線と下に伸びた直線が無限遠点という一点で交わると説明しても良いかもしれません。
個人的にはビーチボールにこの図をプリントして貼り付けて上下に伸びた直線をビーチボールにマジックで書き込んで行くと裏側で交わるという感じで現実世界に落とし込んで理解しています(このアイディアは1点コンパクト化という位相空間論でよく使われるアイディアです)。
定義から $y$ 座標が $0$ になる点 $3P$ は2倍すると $O$ になるということも見てみましょう。
$3P + 3P$ は $3P$ を通る接線を引いて楕円曲線と交わるところを求めるのでした。しかしこれも先程の例同様に縦にまっすぐ伸びて交わりません。
なのでこれも無限遠点で交わると解釈し、 $3P + 3P = 6P = O$ と図を見ても理解できます。
また、 $P + 4 P = 5P$ の箇所ですが、実は $P$ と $4P$ を結ぶ直線と楕円曲線の交点を求めると $4P$ の点が重解として現れます。
そのため交点を $4P$ として、その $x$ 軸対称な点なので $5P$ の位置が下に来ることになります。
ともあれ$P=(2,3)$という点が全ての有理数解(この場合は全てがたまたま整数解になりました)を生成しています。
「 $P$ の足し算以外に解があるかもしれないじゃないか!」と思われた方もいらっしゃるかもしれませんが、ないことが知られています(割愛)。
別の例を見てみましょう。
y^2 = x^3 - 4
という楕円曲線を考えます。
$P = (2,2)$ とするとこれも $4=8-4$ より楕円曲線上の点となります。
この$P$を足しまくってみると以下の結果を得ます。
\begin{eqnarray}
P &=& (2,2)\\
2P &=& (5,-11)\\
3P &=& \left(\frac{106}{9}, \frac{1090}{27} \right)\\
4P &=& \left(\frac{785}{484}, -\frac{5497}{10648} \right)\\
5P &=& \left(\frac{151322}{3721}, -\frac{58862702}{226981} \right)\\
6P &=& \left(\frac{8045029}{2673225}, \frac{21077984917}{4370722875} \right)\\
7P &=& \left(\frac{5495994962}{1957089121}, -\frac{368819269296622}{86579665623919} \right)\\
\end{eqnarray}
なんだか凄いことになりました
今回の例は実は無限個の有理数解が存在する例です。
しかも全ての有理数解は $nP$ という形で表せることができる例です( $nP$ 以外に有理数解が存在しないことを証明する必要がありますが割愛)。
$P = (2,2)$ という点が全ての有理数解を生成するので生成元と呼ばれたりします。
どちらの例を見ても上述した
「どんな楕円曲線 $E$ に対しても、 $E$ 上に有限個の有理点 $P_1,P_2,\ldots,P_n$ が存在して、全ての $E$ 上の有理点は $P_i$ の線形和で表す事ができる」
という主張の例になっています。
この場合は有限個というのが1つの $P$ の和で表せるということですね。
では2個以上の点で生成する楕円曲線の例はどんなのがあるんだろうとか、実はないんじゃないかとか、楕円曲線の係数から判定できないかとか、
**代数体 $k$ 上の楕円曲線 $E$ について $E$ の点のなすアーベル群 $E(k)$ のランクは、 $E$ に伴うハッセ・ヴェイユ $L$-関数 $L(E, s)$ の $s = 1$ における零点の位数ではないか!?**とか予想が出てくるわけですね。
最後の予想が有名なBSD予想というやつで、解けたらクレイ数学研究所から100万ドルもらえます。頑張りましょう。
余談ですが、この予想めちゃくちゃ成立しそうだし綺麗すぎるでしょ……というのがはじめて見た時の個人的な感想でした。
簡単な式の有理数解、整数解を求めるという大学入試の整数問題みたいな問題からスタートしましたが、段々と闇が深くなってきました。
このへんで切り上げましょう。
RSA暗号
楕円曲線暗号はRSA暗号と同じように公開鍵と秘密鍵からなる暗号です。
公開鍵と秘密鍵の仕組みは凄く簡単で、マンションの郵便ポストみたいな仕組みです。
皆さんはマンションの郵便ポストみたいな個人のポスト(公開鍵)を持っています。
そこには郵便局員さんやチラシを配るポスティングの方や佐川やヤマトの方が投函できます。
投函された荷物を皆さんだけの番号(秘密鍵)で開けることができるという仕組みが公開鍵と秘密鍵です。
仮に郵便ポストの鍵が4桁の番号だったりすると他の人が開けようとするには1万通り試さなければならず、これが鍵の安全性を担保しています。
RSA暗号に関してはこの記事がとてもわかり易いですし、いろんな解説記事/解説動画があるため他所に譲ることとします。
色々とありますが、なぜ鍵を持つ人は簡単に復元できて、鍵を持たない人には復元できないのかという話を一言でまとめると、
**「掛け算は簡単だが、素因数分解は難しい」**という一言になります。
高校数学などで多項式の展開は簡単だけど因数分解は難しいなと思った経験、皆さんにもありませんでしょうか。それです。
計算例や数学的な仕組みを話そうと思ったのですが今回のテーマとはややズレるのでそれはまた今度にします(あるのか!?)
有限体
では次に楕円曲線暗号の話と行きたいのですが、その前に有限体の話をしないといけません。
段々長くなって来て申し訳ないのですが、有限体はそんなに難しい話じゃないのでもう少しです。
$p$ を素数とします。
整数を $p$ で割った余りの世界で足し算引き算掛け算割り算を行えるということを見ていきます。
この $p$ で割った余りの世界での等式を $a \equiv b \mod p$ と書く決まりがあります。
例えば$$ 11 \equiv 4 \mod 7$$などと書いたりします。
「11を7で割ると余りが4なんだなあ」ということがこの式を見ると分かることです。
また、この $p$ で割った余りの数の集合を有限体といい、 $\mathbb{F}_p$ で表すことにします。
例えば $p = 7$ とします。7で割った余りの世界なので
$$\mathbb{F}_7 := \{\ 0,1,2,3,4,5,6 \ \}$$ になります。
この世界での計算実例を見ていくと、
$$1 + 6 \equiv 0 \mod 7 \
2 - 3 \equiv 6 \mod 7 \
3 * 4 \equiv 5 \mod 7 \
5 * 2^{-1} \equiv 6 \mod 7
$$
となります。pythonで書けば
>>> (1 + 5) % 7
6
>>> (2 - 3) % 7
6
>>> (3 * 4) % 7
5
みたいな計算をしただけなので難しくないことがおわかりいただけると思います。
ここで割り算に関して注意があります。
$2^{-1}$ というのは$2$に掛けると$1$になる数なのでそれを探す必要があります。
今回は $2 * 4 = 8 \equiv 1 \mod 7$ なので $2^{-1} \equiv 4 \mod 7$がすぐに見つかり、 $5 * 2^{-1} \equiv 5 * 4 \equiv 20 \equiv 6 \mod 7$ と暗算でも計算可能ですが、一般の素数でこの操作を行うのはかなり難しいです。
しかしこの逆元を見つける一般的な操作として、フェルマーの小定理というものがあり、それを用いれば逆元が単純計算で出てくるので紹介します。
定理[Fermat]. 素数 $p$ と互いに素な整数 $a$ について $$ a^{p-1} \equiv 1 \ \text{mod} \ p $$
いくつか例を見てみると確かに成立していることが分かります。
>>> 3 ** 6 % 7
1
>>> 2 ** 6 % 7
1
>>> 3 ** 4 % 5
1
式で書くと以下のようになります。右肩の数が $p-1$ になっていることに注目して下さい。
\begin{eqnarray}
3^6 & \equiv & 1 \text{ mod } 7 \\\
2^6 & \equiv & 1 \text{ mod } 7 \\\
3^4 & \equiv & 1 \text{ mod } 5
\end{eqnarray}
証明.
$1,2, \ldots, p-1$ を考えるとこれらはどの数も $p$ と互いに素となる。
これらに $a$ を掛けた数 $a, 2a, \ldots, (p-1)a$ を考える。
ここでこれらの積は $p$ で割ると余りが一致すること、すなわち、
$$(p-1)! \equiv a^{p-1}(p-1)! \text{ mod }p$$を示す。
$1 \leq i < j \leq p-1$ に関して $ai \equiv aj \text{ mod }p$ と仮定すると
$$a(j-i) \equiv 0 \text{ mod } p$$ となるが、 $0 < j - i < p-1$ と $a$ が $p$ と互いに素なことよりこれは起こり得ない。
よって $i \neq j$ ならば $ai$ と $aj$ が mod $p$ で合同になることはない。以上のことから
$$(p-1)! \equiv a^{p-1}(p-1)! \text{ mod }p$$ が従う。よって
$$ (a^{p-1} - 1)(p-1)! \equiv 0 \text{ mod } p$$ となり、$(p-1)!$は $p$ と互いに素なことより
$$a^{p-1} - 1 \equiv 0 \text{ mod } p$$ を得る。 [証明終]
まとめると、フェルマーの小定理より $a^{-1} = a^{p-2}$ であることが確定するので、割り算もこれで比較的簡単に行えることが分かりました。
先程の $5/2 \equiv 6 \mod 7$ という計算も $2^{-1} \equiv 2^5 \equiv 4 \mod 7$ より $5/2 = 5 * 4 = 20 \equiv 6 \mod 7$ という計算から従います。
ともあれ色々やりましたが有限体というのは素数 $p$ で割った世界で計算してるだけなんやなということを実感してもらえれば幸いです。
楕円曲線暗号
ようやく楕円曲線暗号に入ります。
今までは楕円曲線を有理数体上でやっていましたが、これからは有限体上で計算します。
有理数などでやるとどうしても無限になってしまうため、素数$p$で割った世界で有限に落とし込んでいるのだと思います。
本当はここで $p$ で割ることにより素数 $p$ ごとの個性が楕円曲線に反映されて様々な現象がおきるのですが、そこは今回はそこまで踏み込まずに目をつぶることにします。
(キーワードとしては良い還元(good reduction)などです)
実例を見ていきましょう。上述の例で挙げた楕円曲線
$$y^2=x^3+1$$
を $p=7$ として計算してみましょう。
すると $(x,y)$ のペアは高々有限個なので(49通り)全部調べればいいわけです。
全部調べるコードを書こうと思ったのですが、素晴らしいサイトを見つけました。
このサイトの表をお借りすることにします。
楕円曲線上の点は代入すれば簡単に確かめられますが、足し算はどうなるのでしょうか?
これは上述した激しい計算を有限体 $\mathbb{F}_p$ 上で行うことで計算が可能となります。
実装してみましょう。
class EllipticCurveModPrimeNum():
def __init__(self, a, b, c, d, prime_number):
if a == 0:
raise ValueError("a=0 is forbidden!")
if not is_prime(prime_number):
raise ValueError("{} is not prime!".format(prime_number))
self.a = a % prime_number
self.b = b % prime_number
self.c = c % prime_number
self.d = d % prime_number
self.p = prime_number
def isin(self, pt):
if pt == 0:
return True
x, y = pt[0] % self.p , pt[1] % self.p
value = y**2 - self.a * (x ** 3) - self.b * (x**2) - self.c * x - self.d
if value % self.p == 0:
return True
return False
def sum(self, pt_1, pt_2):
if not self.isin(pt_1):
raise ValueError("{} is not in the elliptic curve".format(pt_1))
if not self.isin(pt_2):
raise ValueError("{} is not in the elliptic curve".format(pt_2))
if pt_1 == 0:
return pt_2
if pt_2 == 0:
return pt_1
x1, y1 = pt_1[0] % self.p, pt_1[1] % self.p
x2, y2 = pt_2[0] % self.p, pt_2[1] % self.p
if x1 != x2:
x3 = ((self.a ** (self.p - 2) * (y2-y1) ** 2 * (x2-x1) ** (2 * self.p - 4) ) % self.p \
- (self.b * self.a ** (self.p - 2)) % self.p\
- x1 - x2
) % self.p
y3 = ((-1 * (y2-y1) * (x2-x1) ** (self.p - 2) * x3 ) % self.p \
+ (y2*x1 - y1*x2) * (x2 - x1) ** (self.p - 2) % self.p
) % self.p
return (x3, y3)
if x1 == x2 and y1 == -1 * y2 % self.p :
return 0
if x1 == x2 and y1 != -1 * y2 % self.p:
x3 = ((4 * self.a * y1 ** 2 % self.p) ** (self.p - 2) % self.p *\
(self.a ** 2 * x1 ** 4 \
- 2 * self.a * self.c * x1 ** 2 % self.p\
- 8 * self.a * self.d * x1 % self.p
- 4 * self.b * self.d % self.p)
) % self.p
y3 = ((8 * self.a * y1 ** 3 % self.p) ** (self.p - 2) % self.p *\
(self.a ** 3 * x1 ** 6 % self.p \
+ 2 * self.a ** 2 * self.b * x1 ** 5 % self.p\
+ 5 * self.a ** 2 * self.c * x1 ** 4 % self.p \
+ 20 * self.a ** 2 * self.d * x1 ** 3 % self.p\
+ (20 * self.a * self.b * self.d % self.p - 5 * self.a * self.c ** 2 % self.p) % self.p * ((x1 ** 2) % self.p) % self.p\
+ (8 * self.b ** 2 * self.d % self.p - 2 * self.b * self.c ** 2 % self.p - 4 * self.a * self.c * self.d % self.p) * (x1 % self.p) % self.p \
+ (4 * self.b * self.c * self.d % self.p - 8 * self.a * self.d ** 2 % self.p - self.c ** 3 % self.p) % self.p )
) % self.p
return (x3, y3)
なんだか激しくなってしまいましたが $\mod p$ を取る操作を適宜行ってできるだけ桁あふれを防ぐということをやっています。
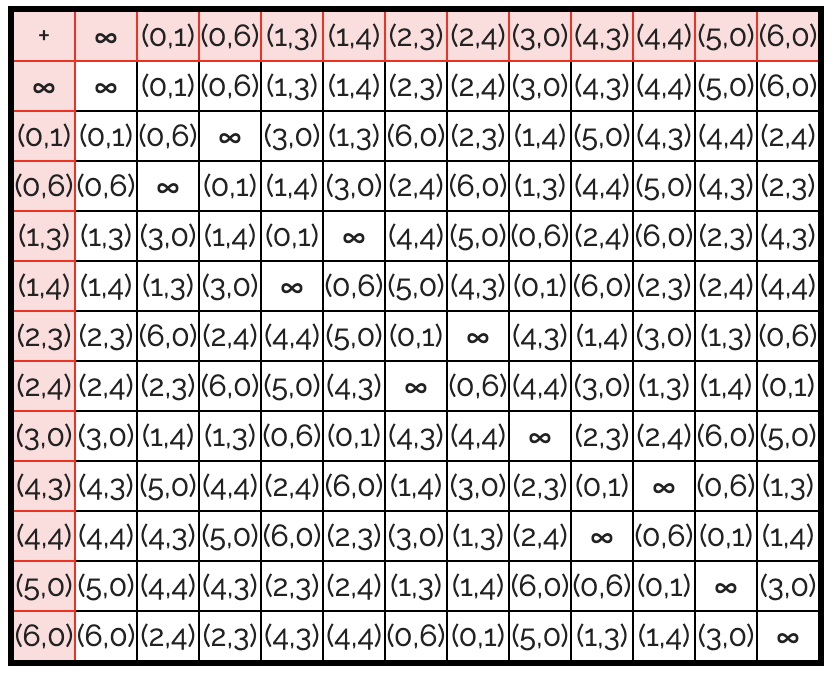
# y^2 = x^3 + 1 mod 7
ell = EllipticCurveModPrimeNum(1,0,0,1,7)
pt1 = (0,1)
pt2 = (1,3)
print(ell.sum(pt1, pt2))
とすると$(3, 0)$が返ってきたので下記の表と一致していることが確かめられます。
他のケースも色々試してみても下記の表と一致していました。
さて、これで楕円曲線暗号の準備が整いました。
今回はAliceとBobの署名に関するやり取りで見ていくとします。
状況:
AliceはBobにメッセージ「お金貸して」とメッセージを送りたい。
Bobは本当にAliceからそのメッセージが来たのかを確認したい。
Aliceは詐欺などではなく自分であることを証明したい。
自分自身であることを証明するためにAliceはBobに以下の物を送ります。
1. メッセージ
2. メッセージを元にAliceの秘密鍵で暗号化した値2つ、これを署名1, 署名2と呼びます
3. 公開鍵
Bobは以下の手続きを行いAliceであることを確認します。
1. 署名1とメッセージ、公開鍵を使って署名2'を計算
2. この署名2'という値が実際に送られてきた署名2と同じものであることを確認
以上の流れでAliceは自分自身のメッセージであることを証明することになります。
これらを実際に楕円曲線を使って見ていきましょう!
楕円曲線暗号では前提として以下のことはお互い知っているものとします。共通言語みたいなものです。
楕円曲線 $E$、素数 $p$、そして楕円曲線上の点 $G$、この $G$ を基準点と呼ぶことにします。
さらに、$G$ 自身を何回足せば元に戻るかという数字を $r$ とします。
定義より $rG = G$ を満たします。
またメッセージを数値化するハッシュ関数もお互い共通のものを使うとします。
Aliceは秘密鍵と公開鍵を作成します。
秘密鍵は整数 $s$ です。公開鍵は $G$ を $s$回足した点 $sG$ です。$sG = W$ と表すことにします。
ここで足し算はベクトルの足し算ではなく楕円曲線上の足し算を行っていることに注意して下さい。
Aliceはメッセージ、署名1、署名2、公開鍵を送るのでした。
では今から署名1と署名2を作成します。(署名1, 署名2をそれぞれ $c$, $d$ とします)
ここからやたら数学になります。
まずメッセージ $m$ をハッシュ化した値を $f$ とします。
次に整数 $u$ を持ってきます。
これは何でも良いのですが、簡単のため、$r$ より小さい数字を取ることにします。
$G$ を $u$ 回足した点を $V = uG = (x_v, y_v)$ とします。
はい!ここで署名1こと $c$ という整数が作れます!
$c \equiv x_v \mod p$ として $x_v$ を $p$ で割った余りで $c$ を定義します。
次に署名2こと $d$ ですが、
$d \equiv u^{-1} (f + sc) \mod p$ としてやはり $p$ で割った余りで $d$ を定義します。
$u^{-1}$ は $p$ で割った余りの世界の逆元であることに注意します。
やたらよく分からない操作をしましたが、これであとは $c$, $d$, $W$ の座標とメッセージを送るだけです。
次にBob側で復元を行っていく操作を見てみます。
Bobは送られてきた謎の数字を元に署名1もどきを計算して実際に署名1 $c$ と一致するのかを確かめるのでした。
では署名1もどきを計算していきましょう。署名1もどきを $c'$ とします。
Bobはまずハッシュ関数を使ってメッセージのハッシュ値 $f$ を計算することができます。
次に以下の点 $P$ を計算します。
$$
P = \frac{f}{d}G + \frac{c}{d}W = \frac{f+sc}{d}G
$$
上の計算は $W = sG$ だったことを使っています。
この $P$ の座標を $(x_p, y_p)$ とした時に、x座標の余りを計算した $c' \equiv x_p \mod p$ が署名1もどきとなります。
この時 $c' = c$ ならAliceからのメッセージであることが確認できるわけです。
$d$ というのは $\frac{f+sc}{u}$ でしたので正しい署名であれば一致するわけですね。
とまあ流れはわかったとしますが、これなにをしたの?感が否めません。
この暗号のキモとなる点は離散対数問題というものになります。
これは $P, G$ が分かっていても $P = nG$ となる $n$ はすぐには見つからないということに起因しています。
我々の安全は楕円曲線によって担保されているということが何となく分かってきたところで今回の話はおしまいです。
参考文献
この記事を書くにあたり以下の記事を参考にしました。
記事の作成者の方々に感謝致します。
RSA暗号の仕組みと安全性
https://mathtrain.jp/rsaango
RSAに関して暗号化のやり方、復元のやり方が分かりやすく解説されている。
整数論の最前線 楕円曲線の数論幾何
https://www.math.kyoto-u.ac.jp/~tetsushi/files/Galois_fest_ito_200705.pdf
楕円曲線に関する未解決問題や楕円曲線に関する広大な背景に関して平易な言葉で述べられている。
特に知識は仮定せずにBSD予想や谷山志村予想や佐藤テイト予想を紹介していて迫力がある。
楕円曲線暗号アルゴリズムを理解する
https://techracho.bpsinc.jp/yoshi/2019_08_16/79280
この記事を書くにあたり参考にしました。とても分かりやすいです。
計算する立場からの楕円曲線論入門
http://www.comp.tmu.ac.jp/s-yokoyama/lectures/2015-2018/files/2014Yamagata.pdf
東京都立大学(執筆時点では九州大学所属)の横山さんの解説記事。
sageというpythonベースの統合ソフトウェアを用いて楕円曲線に関する面白い話題を解説されています。
横山さんは大学時代の先輩にあたるのですが、昔から解説が上手でその本領が発揮されている良記事です。
その他楕円曲線暗号の署名に関する計算方法を下記の記事で学びました。
https://jp.globalsign.com/documentsigning/about/digitalsignature.html
最後に
Supershipではプロダクト開発やサービス開発に関わる人を絶賛募集しております。
ご興味がある方は以下リンクよりご確認ください。
Supership株式会社 採用サイト
是非ともよろしくお願いします。