前回以降に試したことを記載していきます。
(1) h-swish(活性化関数)
ReLUと同等の性能で、Swishと同等の精度が出るようなので試してみます。
(2) TanhExp(活性化関数)
Mishより精度が良いとのこと。
(3) Flooding(正則化)
損失関数の値を一定以上の値になるように調整することで過学習を防ぐ手法
(4) Nesterovの加速勾配法(最適化)
実装変更により未対応となっておりました。この機会に対応します。
プログラムは、「ディープラーニングを実装から学ぶ(8)実装変更」を利用します。
今回もMNISTを利用し精度を検証します。
h-swish
前回、ディープラーニングを実装から学ぶ(8-2)活性化関数(Swish,Mish)でSwishを試してみました。
h-swishは、ReLUと同等の性能で、Swishと同等の精度が出るようなので試してみます。
h-swishは、次の式で表されます。
f_{h-swish}(x) = x\cdot\frac{\mathrm{ReLU6}(x+3)}{6}
ReLU6は、ディープラーニングを実装から学ぶ(7-1)その他(活性化関数~MaxOut、ReLU関連)一定の値以上を定数とするReLUで紹介しています。n=6の場合に相当します。式は、次の通りです。
f_{ReLU6}(x_i) = \left\{
\begin{array}{ll}
6 & (x_i \gt 6) \\
x_i & (6 \ge x_i \gt 0) \\
0 & (x_i \leq 0)
\end{array}
\right.
h-swishを場合分けして書くと以下となります。
f_{h-swish}(x_i) = \left\{
\begin{array}{ll}
x_i & (x_i \gt 3) \\
x_i\cdot\frac{x_i+3}{6} & (3 \ge x_i \gt -3) \\
0 & (x_i \leq -3)
\end{array}
\right.
-3~3以外は、ReLUと同じですね。
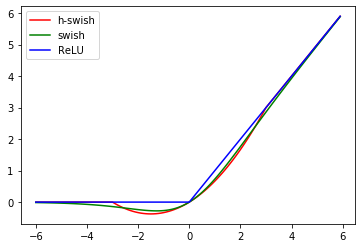
グラフにしてみましょう。ReLU,Swishとの比較です。
順伝播
順伝播は、場合分けした式をそのまま実装しました。
def h_swish(u):
return np.where(u > 3, u, np.where(u > -3, u*(u+3)/6, 0))
せっかくなので、ReLU6を拡張し、6の部分を指定できるようにします。
f_{h-swish}(x_i) = \left\{
\begin{array}{ll}
x_i & (x_i \gt \frac{n}{2}) \\
x_i\cdot\frac{x_i+\frac{n}{2}}{n} & (\frac{n}{2} \ge x_i \gt -\frac{n}{2}) \\
0 & (x_i \leq -\frac{n}{2})
\end{array}
\right.
実装です。
def h_swish(u, n=6):
return np.where(u > n/2, u, np.where(u > -n/2, u*(u+n/2)/n, 0))
逆伝播
勾配計算は難しくないですね。場合分けをそのまま微分すればOKです。
f'_{h-swish}(x_i) = \left\{
\begin{array}{ll}
1 & (x_i \gt \frac{n}{2}) \\
\frac{2x_i+\frac{n}{2}}{n} & (\frac{n}{2} \ge x_i \gt -\frac{n}{2}) \\
0 & (x_i \leq -\frac{n}{2})
\end{array}
\right.
実装です。
def h_swish_back(dz, u, z, n=6):
return dz * np.where(u > n/2, 1, np.where(u > -n/2, (2*u+n/2)/n, 0))
実行
MNISTの予測を行います。
プログラムは、「ディープラーニングを実装から学ぶ(8)実装変更」を利用します。
データの読み込み、正規化
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
data_normalizer = create_data_normalizer(min_max)
nx_train, data_normalizer_stats = train_data_normalize(data_normalizer, x_train)
nx_test = test_data_normalize(data_normalizer, x_test)
モデル定義
model = create_model(nx_train.shape[1]) # 28*28
model = add_layer(model, "affine1", affine, 100)
model = add_layer(model, "h_swish1", h_swish, n=n)
model = add_layer(model, "affine2", affine, 50)
model = add_layer(model, "h_swish2", h_swish, n=n)
model = add_layer(model, "affine3", affine, 10)
model = set_output(model, softmax)
model = set_error(model, cross_entropy_error)
optimizer = create_optimizer(SGD)
実行
epoch = 50
batch_size = 100
np.random.seed(10)
model, optimizer, learn_info = learn(model, nx_train, t_train, nx_test, t_test, batch_size=batch_size, epoch=epoch)
結果
input - 0 784
affine1 affine 784 100
h_swish1 h_swish 100 100
affine2 affine 100 50
h_swish2 h_swish 50 50
affine3 affine 50 10
output softmax 10
error cross_entropy_error
0 0.07916666666666666 2.3561063616088465 0.0815 2.353008956466937
1 0.8613 0.47874365694349547 0.924 0.2609216647266223
2 0.9320166666666667 0.22935854952811313 0.9426 0.18980591095531943
3 0.94865 0.17355557311614847 0.948 0.16567329627123964
4 0.9576666666666667 0.14161654725603698 0.9636 0.12227732670336343
5 0.9643 0.12006337563665476 0.9651 0.11190433092212797
6 0.9697833333333333 0.10292181135390342 0.9676 0.10740120541405829
7 0.9731333333333333 0.09016856465998503 0.9706 0.09454420693977063
8 0.9752666666666666 0.08128841646680009 0.9687 0.09667347834562377
9 0.9785833333333334 0.0726699466827525 0.9718 0.0894811548213494
10 0.9802333333333333 0.06544205573500171 0.9746 0.08338806115049387
11 0.98205 0.059687812270458634 0.9726 0.0861182444301773
12 0.9835166666666667 0.054715464958141315 0.974 0.08564706979449492
13 0.9845666666666667 0.04978882472083735 0.9753 0.08210068715417576
14 0.9862666666666666 0.04526453034479706 0.9753 0.07932560522244121
15 0.9870833333333333 0.04172984871222474 0.9748 0.08157439317509485
16 0.9882833333333333 0.038348839466811654 0.9771 0.07570351077747177
17 0.9892666666666666 0.034723549340483995 0.9764 0.07956000927460419
18 0.9907333333333334 0.03180313922918117 0.9762 0.07858554907198075
19 0.9912666666666666 0.02924037919063334 0.9764 0.07865272976211594
20 0.99265 0.026184990511601967 0.9773 0.0794230992599565
21 0.9929833333333333 0.024032628385138515 0.9779 0.08049788897132074
22 0.9941666666666666 0.022063808726783908 0.9779 0.0784229459901341
23 0.9943166666666666 0.02025218479131825 0.9776 0.08121503711484651
24 0.99555 0.018251131876931562 0.9747 0.09080676027510731
25 0.9955166666666667 0.017108533096466785 0.9763 0.08385507393126691
26 0.9964833333333334 0.015266957319092417 0.978 0.08203356458257523
27 0.9967666666666667 0.013949909689762745 0.9791 0.08336950634327407
28 0.9970166666666667 0.01310236804507814 0.9781 0.08373749456062173
29 0.9976333333333334 0.011523165728934278 0.978 0.08371774425398823
30 0.99805 0.010386231232303174 0.9796 0.07911908642468785
31 0.9981833333333333 0.009611627899225136 0.978 0.0846851716323456
32 0.9983666666666666 0.008631802674194087 0.9785 0.08471463263044288
33 0.9984166666666666 0.008154108198403662 0.979 0.08503833624865097
34 0.9988666666666667 0.007209576659560477 0.9796 0.08706478140965124
35 0.9990833333333333 0.006477061312654932 0.979 0.08674659828026123
36 0.9991666666666666 0.005983977401353051 0.9791 0.08552447530273263
37 0.9992666666666666 0.0055666794938792575 0.9793 0.08634799867690887
38 0.99955 0.004909938871773991 0.9781 0.0901079865272064
39 0.9995333333333334 0.004455956313217781 0.9794 0.08778692922304444
40 0.99965 0.004357646017530345 0.9784 0.08951540694507558
41 0.9997166666666667 0.003757533450244203 0.9782 0.09090586759893682
42 0.9996166666666667 0.0035934700999595134 0.9786 0.09099227519698058
43 0.9996666666666667 0.003386469508559878 0.9778 0.09767922822717794
44 0.9998333333333334 0.0030207525127624556 0.9777 0.09776663543848799
45 0.9998833333333333 0.0029249262245713663 0.9788 0.09243620892932264
46 0.9999 0.002607049075994687 0.9785 0.09239721474326253
47 0.99995 0.0024278908950352463 0.9787 0.0952917966774719
48 0.9999333333333333 0.0023103529546672037 0.9795 0.09541757934847203
49 0.9999333333333333 0.0022159289643019307 0.9788 0.09551892930786073
50 0.9999833333333333 0.0020028990461559877 0.9788 0.09513261161265309
所要時間 = 0 分 43 秒
比較
基本の実行
ReLU、Swishと比較します。精度は、ReLUより若干よく、性能はほぼReLUと同じです。ただ、Swishもそれほど遅いわけではありません。
| 活性化関数 | 学習正解 | テスト正解 | テスト最高 | TS95% | TS97% | TS98% | 所要時間 |
|---|---|---|---|---|---|---|---|
| ReLU | 100.00 | 97.85 | 97.88 | 2 | 5 | - | 41秒 |
| Swish | 100.00 | 98.01 | 98.05 | 3 | 7 | 33 | 52秒 |
| h-swish | 100.00 | 97.88 | 97.96 | 4 | 7 | - | 43秒 |
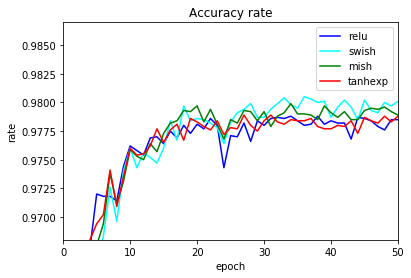
エポックごとのテストデータの正解率をグラフ化します。
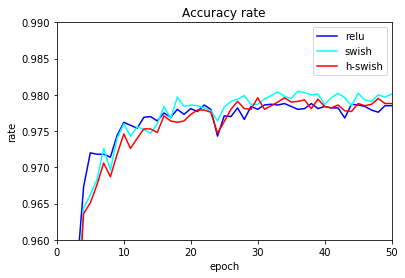
エポック数が少ないときは、Swishとh-swishは似た傾向となってますね。
n変更
nを変更し試してみました。nをうまく調整するれば精度が向上する場合もあるようです。
| 活性化関数 | n | 学習正解 | テスト正解 | テスト最高 |
|---|---|---|---|---|
| h_swish | 1 | 100.00 | 98.01 | 98.03 |
| h_swish | 2 | 100.00 | 97.93 | 98.00 |
| h_swish | 3 | 100.00 | 97.88 | 97.98 |
| h_swish | 4 | 100.00 | 98.03 | 98.08 |
| h_swish | 5 | 100.00 | 98.01 | 98.04 |
| h_swish | 6 | 100.00 | 97.88 | 97.96 |
| h_swish | 7 | 99.99 | 97.87 | 97.90 |
| h_swish | 8 | 99.96 | 97.78 | 97.88 |
| h_swish | 9 | 99.96 | 97.73 | 97.82 |
| h_swish | 10 | 99.93 | 97.71 | 97.83 |
| ReLU | - | 100.00 | 97.85 | 97.88 |
| Swish | - | 100.00 | 98.01 | 98.05 |
学習係数変更
学習係数0.5変更してみます。たまたまかもしれませんが、大幅に精度が向上しました。
| 活性化関数 | 学習正解 | テスト正解 | テスト最高 |
|---|---|---|---|
| ReLU | 100.00 | 98.07 | 98.12 |
| Swish | 100.00 | 98.07 | 98.13 |
| h-swish | 100.00 | 98.30 | 98.31 |
ノード数変更
ノード数を100-50から200-100に拡大してみます。
| 活性化関数 | 学習係数 | 学習正解 | テスト正解 | テスト最高 |
|---|---|---|---|---|
| ReLU | 0.1 | 100.00 | 98.01 | 98.08 |
| Swish | 0.1 | 99.99 | 98.10 | 98.15 |
| h-swish | 0.1 | 99.99 | 98.01 | 98.07 |
| ReLU | 0.5 | 100.00 | 98.29 | 98.31 |
| Swish | 0.5 | 100.00 | 98.30 | 98.37 |
| h-swish | 0.5 | 100.00 | 98.36 | 98.39 |
h-swishは、ReLU同等か、Swish並みの精度を出せることがわかりました。
Swishの代わりに、h-swishを使ってもよいのではないでしょうか、
TanhExp
h-swishに続いて、TanhExpです。名前からわかるようにtanhとexpを使います。tanhを使うMishの改良版というところでしょうか、
Mishのsoftplusの部分がexpになります。
f_{tanhexp}(x) = x\cdot\mathrm{tanh}(e^x)
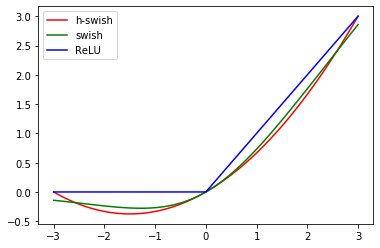
グラフ化し、ReLU,Swish,Mishと比較してみます。
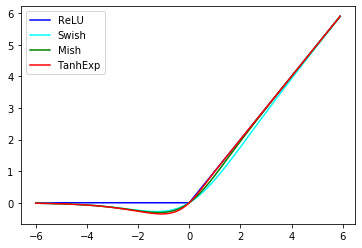
似てますね。-2~2の間を拡大します。
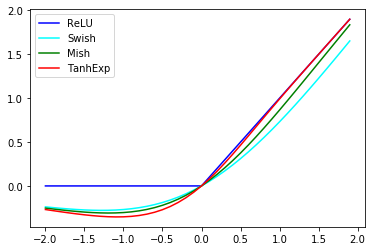
正の部分では、Swish,Mish,TanhExpの順にReLUに近く、負の部分ではその逆ですね。
順伝播
順伝播の実装です。
こちらは、式をそのまま実装すればよいだけです。
def tanhexp(u):
return u * tanh(np.exp(u))
逆伝播
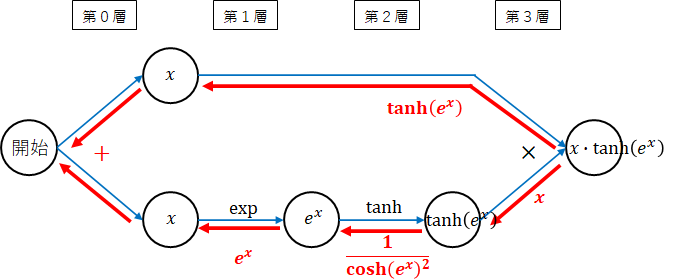
勾配を計算するためのネットワーク図です。Mishのsoftplusをexpに変更したのみです。
$ e^x $の微分は、$ e^x $でしたね。
勾配計算の詳細は割愛します。必要があれば、ディープラーニングを実装から学ぶ(8-2)活性化関数(Swish,Mish)を参照してください。
実装です。
def tanhexp_back(dz, u, z):
return dz * (np.tanh(np.exp(u)) + u / (np.cosh(np.exp(u))**2) * np.exp(u))
これでもよいのですが、$ x $の値が大きい場合、$ \mathrm{cosh}(e^x) $の部分でオーバフローが発生します。
$ \mathrm{tanh} $の微分の式の変換を行います。
\frac{1}{\mathrm{cosh}(x)^2} = 1 - \mathrm{tanh(x)^2}
ここでは、式の変換の詳細については説明しませんので、必要であれば調べてみてください。
実装を以下のように変更します。
def tanhexp_back(dz, u, z):
return dz * (np.tanh(np.exp(u)) + u * (1 - np.tanh(np.exp(u))**2) * np.exp(u))
実行
データの読み込み、正規化は、h-swishと同じです。
モデル定義
model = create_model(nx_train.shape[1]) # 28*28
model = add_layer(model, "affine1", affine, 100)
model = add_layer(model, "tanhexp1", tanhexp)
model = add_layer(model, "affine2", affine, 50)
model = add_layer(model, "tanhexp2", tanhexp)
model = add_layer(model, "affine3", affine, 10)
model = set_output(model, softmax)
model = set_error(model, cross_entropy_error)
optimizer = create_optimizer(SGD)
実行
epoch = 50
batch_size = 100
np.random.seed(10)
model, optimizer, learn_info = learn(model, nx_train, t_train, nx_test, t_test, batch_size=batch_size, epoch=epoch)
結果
input - 0 784
affine1 affine 784 100
tanhexp1 tanhexp 100 100
affine2 affine 100 50
tanhexp2 tanhexp 50 50
affine3 affine 50 10
output softmax 10
error cross_entropy_error
0 0.0833 2.470228617930653 0.0834 2.465403420348584
1 0.8854 0.38858357162157897 0.9327 0.2262694736336025
2 0.9418666666666666 0.1949348000154293 0.9523 0.15860467874378387
3 0.95765 0.14465427913089615 0.9575 0.13903470287021708
4 0.9650833333333333 0.11595679851584827 0.968 0.10755512561336457
5 0.9711833333333333 0.09692344369554036 0.9694 0.10069294348902594
6 0.97495 0.08260391232769612 0.9702 0.09510697685664725
7 0.9783166666666666 0.0717003394974233 0.9741 0.08461778468856011
8 0.9807833333333333 0.06371277466523415 0.9709 0.09134749677378065
9 0.9830833333333333 0.0566792218402545 0.9735 0.083317076841829
10 0.9847 0.050531232358150095 0.976 0.07889912941098867
11 0.9862833333333333 0.045629372265243266 0.9754 0.07956649534803646
12 0.98855 0.04073025860785511 0.9755 0.07761986136826124
13 0.9893166666666666 0.036563829060012 0.9762 0.07747762694537075
14 0.9906 0.03271824181932224 0.9777 0.07384013614230077
15 0.9913166666666666 0.030033478320751553 0.9765 0.07711687419500353
16 0.9925 0.027036091279103294 0.9776 0.07348287436648057
17 0.9935666666666667 0.024343286058487693 0.9781 0.07376986091972655
18 0.9941333333333333 0.0222434899292904 0.9767 0.0747680872509711
19 0.995 0.019908372520617307 0.9786 0.07519133313190618
20 0.9958833333333333 0.017646392056081955 0.9783 0.07429464182176589
21 0.9965666666666667 0.015772591937338796 0.9779 0.07693150109142576
22 0.9967666666666667 0.014404692533559896 0.9776 0.07739097147841713
23 0.9975333333333334 0.012863004719175945 0.9784 0.07825279863214511
24 0.9981 0.011591031352835828 0.9772 0.08415300460381062
25 0.9983333333333333 0.010493076155950699 0.9778 0.07893936569850117
26 0.9984666666666666 0.00946028444350386 0.9777 0.08037724673873071
27 0.99865 0.008679406186674992 0.9789 0.08075106448222731
28 0.9989666666666667 0.007904633070520703 0.978 0.08143180920729907
29 0.999 0.007196727877340475 0.9775 0.08383021677225208
30 0.9993 0.006401549679126232 0.9784 0.08092467062859009
31 0.9994666666666666 0.005737243776156002 0.9789 0.08354051758884838
32 0.9993833333333333 0.005363076379495166 0.9783 0.08384939891478231
33 0.9995833333333334 0.004843408318562353 0.9781 0.0846920093033944
34 0.99955 0.004531412049398901 0.9785 0.08527008327249454
35 0.9997333333333334 0.003956433770971815 0.9784 0.08682703136188279
36 0.9998166666666667 0.003628498653436892 0.9784 0.08585713594655904
37 0.9997833333333334 0.003429941670515467 0.9786 0.08564944578663089
38 0.9999333333333333 0.0030599674971503086 0.9779 0.08770807277637312
39 0.9998833333333333 0.0029091822498929646 0.9777 0.0878078761803294
40 0.9998666666666667 0.002700600205783143 0.9777 0.08881677549254945
41 0.9999 0.0024944002531200786 0.978 0.08952123222663376
42 0.9999666666666667 0.002350002702402667 0.9779 0.09032854671382584
43 0.9999 0.0022250091388379555 0.9784 0.0904079229842052
44 0.9999666666666667 0.0020534014616740816 0.9773 0.09208936505533323
45 0.9999666666666667 0.0019493015577477528 0.9787 0.0896670232930406
46 1.0 0.0018474990046398656 0.9784 0.09123345672949301
47 0.9999833333333333 0.0017308428989611224 0.9782 0.09163227325663607
48 1.0 0.00166639286656076 0.9788 0.09156645205231942
49 0.9999833333333333 0.0016055587244625117 0.9783 0.09283041253202276
50 0.9999833333333333 0.0015068785073926608 0.9788 0.09297598799209969
所要時間 = 1 分 27 秒
比較
基本の実行
ReLU、Swish、Mishと比較します。精度は、ReLUより若干よくなりました。
| 活性化関数 | 学習正解 | テスト正解 | テスト最高 | TS95% | TS97% | TS98% | 所要時間 |
|---|---|---|---|---|---|---|---|
| ReLU | 100.00 | 97.85 | 97.88 | 2 | 5 | - | 41秒 |
| Swish | 100.00 | 98.01 | 98.05 | 3 | 7 | 33 | 52秒 |
| Mish | 100.00 | 97.89 | 97.99 | 3 | 7 | - | 1分33秒 |
| TanhExp | 100.00 | 97.88 | 97.89 | 2 | 6 | - | 1分27秒 |
学習係数変更
学習係数0.5変更してみます。たまたまかもしれませんが、精度が向上しました。
| 活性化関数 | 学習正解 | テスト正解 | テスト最高 |
|---|---|---|---|
| ReLU | 100.00 | 98.07 | 98.12 |
| Swish | 100.00 | 98.07 | 98.13 |
| Mish | 100.00 | 98.24 | 98.26 |
| TanhExp | 100.00 | 98.25 | 98.31 |
ノード数変更
ノード数を100-50から200-100に拡大してみます。
| 活性化関数 | 学習係数 | 学習正解 | テスト正解 | テスト最高 |
|---|---|---|---|---|
| ReLU | 0.1 | 100.00 | 98.01 | 98.08 |
| Swish | 0.1 | 99.99 | 98.10 | 98.15 |
| Mish | 0.1 | 100.00 | 98.15 | 98.21 |
| TanhExp | 0.1 | 100.00 | 98.10 | 98.22 |
| ReLU | 0.5 | 100.00 | 98.29 | 98.31 |
| Swish | 0.5 | 100.00 | 98.30 | 98.37 |
| Mish | 0.5 | 100.00 | 98.26 | 98.35 |
| TanhExp | 0.5 | 100.00 | 98.45 | 98.49 |
学習係数が0.5の時、テスト正解率が98.5近くになりました。
性能上特に問題ない場合、まずは、TanhExpで試してみるのもよいかもしれません。
Flooding
学習時にエポック数を増やしても損失関数の値がほぼ0となり学習が進まないか、過学習が発生しかえってテストデータに対する正解率が悪化していく場合があります。
損失関数の値を一定の値以上にキープし、さらに学習を進めようとするものです。
損失関数に依存せず、汎用的に用いることが可能です。
損失関数を$ E $とした場合、Floodingは、以下の式で表されます。
\tilde{E} = | E-b | + b
絶対値を$ E $が$ b $以上の場合と未満の場合で分けて考えてみましょう。
\tilde{E} = \left\{
\begin{array}{ll}
E & (E \ge b) \\
-E + 2b & (E \lt b)
\end{array}
\right.
この式の値は、必ず$ b $以上になります。損失関数の値が必ず$ b $以上となるわけです。
$ b $はハイパーパラメータとして適切な値を設定します。
実装
損失関数指定時に、$ b $を設定できるようにします。
交差エントロピー誤差に、$ b=0.01 $を設定した例です。
model = set_error(model, cross_entropy_error, b=0.01)
損失関数に上の式を適用していきます。損失関数自体に対応を入れるのではなく、損失関数呼び出し時に対応を行います。
順伝播
学習時の順伝播時は、特に損失関数の値は計算していませんでした。逆伝播時に利用するため、$ b $を指定している場合には、計算を行います。
if "b" in model["error"]["params"]:
err = np.abs(err - model["error"]["params"]["b"]) + model["error"]["params"]["b"]
順伝播関数全体です。
def propagation(model, x, t=None, learn_flag=True):
us = {}
u = x
err = None
weight_decay_sum = 0
# layer
for k, v in model["layer"].items():
# propagation関数設定
propagation_func = middle_propagation
if v["func"].__name__ + "_propagation" in globals():
propagation_func = eval(v["func"].__name__ + "_propagation")
# propagation関数実行
us[k], weight_decay_r = propagation_func(v["func"], u, v["weights"], model["weight_decay"], learn_flag, **v["params"])
u = us[k]["z"]
weight_decay_sum = weight_decay_sum + weight_decay_r
# output
if "output" in model:
propagation_func = output_propagation
# propagation関数実行
us["output"] = propagation_func(model["output"]["func"], u, learn_flag, **model["output"]["params"])
u = us["output"]["z"]
# error
y = u
# 学習時には、誤差は計算しない
if learn_flag == False or "b" in model["error"]["params"]:
if "error" in model:
if t is not None:
err = model["error"]["func"](y, t)
# 重み減衰
if "weight_decay" is not None:
if learn_flag:
err = err + weight_decay_sum
# flooding対応
if learn_flag == False:
if "b" in model["error"]["params"]:
err = np.abs(err - model["error"]["params"]["b"]) + model["error"]["params"]["b"]
return y, err, us
逆伝播
Floodingの勾配を考えます。
\tilde{E} = \left\{
\begin{array}{ll}
E & (E \ge b) \\
-E + 2b & (E \lt b)
\end{array}
\right.
各勾配は、以下のようになります。
\tilde{E'} = \left\{
\begin{array}{ll}
1 & (E \ge b) \\
-1 & (E \lt b)
\end{array}
\right.
$ E < b $の場合に、符号を反転させます。すなわち誤差を減少させる方向とは、逆方向に重みを変化させることになります。このことにより、誤差が$ b $より小さくなると重みを逆方向に更新し誤差を増加させることで、損失関数の値が0にならないようにします。
# flooding対応
if "b" in model["error"]["params"]:
if err < model["error"]["params"]["b"]:
du = -du
逆伝播プログラム全体です。
順伝播で計算した誤差を取得できるようにパラメータにerrを追加しています。
def back_propagation(model, x=None, t=None, y=None, us=None, err=None, du=None):
dus = {}
if du is None:
# 出力層+誤差勾配関数
output_error_back_func = eval(model["output"]["func"].__name__ + "_" + model["error"]["func"].__name__ + "_back")
du = output_error_back_func(y, us["output"]["u"], t)
# flooding対応
if "b" in model["error"]["params"]:
if err < model["error"]["params"]["b"]:
du = -du
dus["output"] = {"du":du}
dz = du
for k, v in reversed(model["layer"].items()):
# back propagation関数設定
back_propagation_func = middle_back_propagation
if v["func"].__name__ + "_back_propagation" in globals():
back_propagation_func = eval(v["func"].__name__ + "_back_propagation")
# back propagation関数実行
dus[k] = back_propagation_func(v["back_func"], dz, us[k], v["weights"], model["weight_decay"], v["calc_du_flag"], **v["params"])
dz = dus[k]["du"]
# du計算フラグがFalseだと以降計算しない
if v["calc_du_flag"] == False:
break
return dz, dus
学習関数
順伝播(propagation関数)、逆伝播(back_propagation関数)間で誤差(err)を受け渡すようにプログラムを変更します。
# 学習
def learn(model, x_train, t_train, x_test=None, t_test=None, batch_size=100, epoch=50, init_model_flag=True,
optimizer=None, init_optimizer_flag=True, shuffle_flag=True, learn_info=None):
if init_model_flag:
model = init_model(model)
if optimizer is None:
optimizer = create_optimizer(SGD)
if init_optimizer_flag:
optimizer = init_optimizer(optimizer, model)
# 学習情報初期化
learn_info = epoch_hook(learn_info, epoch, 0, model, x_train, None, t_train, x_test, t_test, batch_size)
# エポック実行
for i in range(epoch):
idx = np.arange(x_train.shape[0])
if shuffle_flag:
# データのシャッフル
np.random.shuffle(idx)
# 学習
y_train = np.zeros(t_train.shape)
for j in range(0, x_train.shape[0], batch_size):
# propagation
y_train[idx[j:j+batch_size]], err, us = propagation(model, x_train[idx[j:j+batch_size]], t_train[idx[j:j+batch_size]])
# back_propagation
dz, dus = back_propagation(model, x_train[idx[j:j+batch_size]], t_train[idx[j:j+batch_size]], y_train[idx[j:j+batch_size]], us, err)
# update_weight
model, optimizer = update_weight(model, dus, optimizer)
# 学習情報設定(エポックフック)
learn_info = epoch_hook(learn_info, epoch, i+1, model, x_train, y_train, t_train, x_test, t_test, batch_size)
return model, optimizer, learn_info
実行
データの読み込みは、上と同じため省略します。
モデル定義
set_errorに$ b $を設定します。ここでは試しに0.01を設定してみました。
model = create_model(nx_train.shape[1]) # 28*28
model = add_layer(model, "affine1", affine, 100)
model = add_layer(model, "relu1", relu)
model = add_layer(model, "affine2", affine, 50)
model = add_layer(model, "relu2", relu)
model = add_layer(model, "affine3", affine, 10)
model = set_output(model, softmax)
model = set_error(model, cross_entropy_error, b=0.01)
実行
epoch = 50
batch_size = 100
np.random.seed(10)
model, optimizer, learn_info = learn(model, nx_train, t_train, nx_test, t_test, batch_size=batch_size, epoch=epoch)
結果
input - 0 784
affine1 affine 784 100
relu1 relu 100 100
affine2 affine 100 50
relu2 relu 50 50
affine3 affine 50 10
output softmax 10
error cross_entropy_error
0 0.08133333333333333 2.489248983149533 0.0838 2.490209670597171
1 0.8772833333333333 0.42069153907149026 0.9348 0.2241568003492831
2 0.9434833333333333 0.19200015674198498 0.9517 0.15882406339763025
3 0.9583833333333334 0.14041528910871223 0.9557 0.14444191204678322
4 0.9665333333333334 0.11235497483762866 0.9673 0.1092788064509263
5 0.9721333333333333 0.09324761344337475 0.972 0.09688950013342208
6 0.9769333333333333 0.07929764380432314 0.9718 0.093241709446732
7 0.9792833333333333 0.06861578527109287 0.9719 0.08746743219533526
8 0.9817666666666667 0.060831740852681226 0.9715 0.08809369429100987
9 0.98475 0.05304643936074331 0.9743 0.08140080298946577
10 0.9857833333333333 0.047718716514613575 0.9753 0.077965797098391
11 0.9872833333333333 0.042187868958545885 0.9763 0.07583893263174207
12 0.9890833333333333 0.03819651167133632 0.9754 0.07494302396285188
13 0.9901 0.03368049943308557 0.9769 0.074687653268699
14 0.9915833333333334 0.030154755199273322 0.9763 0.07549486972752763
15 0.9925 0.027569454109424844 0.9753 0.07706761564478214
16 0.9932166666666666 0.0256074445260314 0.9779 0.07170363628007224
17 0.9942166666666666 0.022995464300296104 0.9769 0.07495456224823384
18 0.9945833333333334 0.02122916835244918 0.9773 0.07292985074496885
19 0.99535 0.019644436719029667 0.9764 0.07522538140821668
20 0.99605 0.017853675956208643 0.9764 0.07144483285428617
21 0.9966666666666667 0.01698406901775429 0.9767 0.0766446816498703
22 0.9965833333333334 0.015940090862710265 0.979 0.07168177370638634
23 0.9968666666666667 0.0156697597464082 0.9787 0.07279078397761812
24 0.9974666666666666 0.014237919376521708 0.9753 0.08061298835708573
25 0.9971666666666666 0.014191961199262157 0.9772 0.07624793624360277
26 0.9977333333333334 0.013376114725637326 0.9762 0.07361203115495082
27 0.9975 0.013170889910149723 0.9776 0.07439523988284298
28 0.9973833333333333 0.013424458808224479 0.9772 0.07564105588179061
29 0.9982333333333333 0.01181406298220755 0.9773 0.074051296241924
30 0.9980333333333333 0.012168664311281965 0.9755 0.07622357096410763
31 0.9981 0.011638764805973882 0.9758 0.07830546192867295
32 0.9982666666666666 0.011701162836222235 0.9738 0.08337507996704895
33 0.9981166666666667 0.011584108362914647 0.9789 0.07140721433185196
34 0.99815 0.011373570979540512 0.9772 0.0808122149526131
35 0.9984333333333333 0.01100584151258856 0.9779 0.07411217156760615
36 0.9985166666666667 0.011417534186121599 0.9786 0.0741385184041246
37 0.9984166666666666 0.01116486227367655 0.9774 0.07727210740631794
38 0.9983833333333333 0.010871662341680627 0.9783 0.07682022649265897
39 0.9985166666666667 0.010868234338663657 0.9757 0.07818572611680628
40 0.99885 0.010781309610722366 0.9755 0.0786724875554655
41 0.9985833333333334 0.010845845440437814 0.9782 0.07323057390511194
42 0.9984833333333333 0.010765373707664611 0.9764 0.07901560864405806
43 0.9987833333333334 0.010629761064620382 0.9769 0.07602863745367182
44 0.9985666666666667 0.010794079702832299 0.9733 0.08902100317262684
45 0.9989666666666667 0.010367395540446682 0.9783 0.0741063786068936
46 0.99905 0.010449935589486866 0.9785 0.07415012949719588
47 0.9988833333333333 0.010280173179660996 0.9771 0.07738817694641274
48 0.9988 0.010228442793313376 0.9748 0.08456348438104741
49 0.9989666666666667 0.010470726552106678 0.9775 0.07807122095710674
50 0.99895 0.010601526876873485 0.976 0.08027436734990587
所要時間 = 0 分 42 秒
比較
b=0.01
b=0.01とFloodingなし(b=0)との比較です。
50エポック後の精度は悪くなりました。学習が安定していないようです。
| 活性化関数 | 学習正解 | テスト正解 | テスト最高 | TS95% | TS97% | TS98% |
|---|---|---|---|---|---|---|
| b=0 | 100.00 | 97.85 | 97.88 | 2 | 5 | - |
| b=0.01 | 99.90 | 97.60 | 97.90 | 2 | 5 | - |
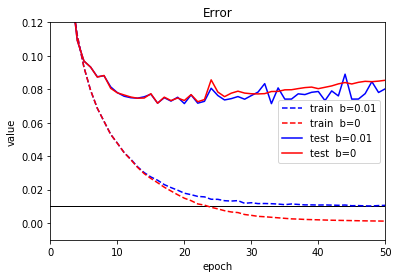
エポックごとの誤差をグラフ化します。赤は、Floodingなし、青がb=0.01の場合です。
青の学習データの誤差が$ b $で指定した0.01に近づいています。$ b $が正しく適用できていることがわかります。
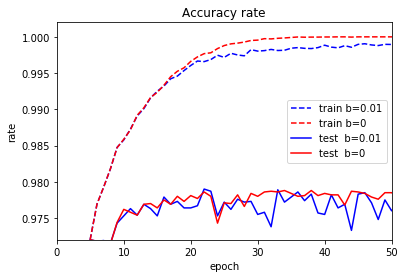
正解率のグラフも見てみましょう。
テストデータの正解率(青の実線)を見てみましょう。乱高下しています。誤差が$ b $以下になると逆方向(誤差が増える方向)に重みを更新するため、正解率が減りまた増えるの繰り返しになるのだと思います。
Floodingなしの場合と比較すると精度が向上する場合もありますが、上下しているため適切な場所で学習を打ち切るのが難しそうです。
500エポックまで拡大し、誤差、正解率をグラフ化してみます。
Floodingなしの場合(赤の実線)、テストデータの誤差がどんどん増えて過学習に陥っていることがわかります。
それに対して、Floodingありの場合(青の実線)の場合は、誤差が一定を保っています。
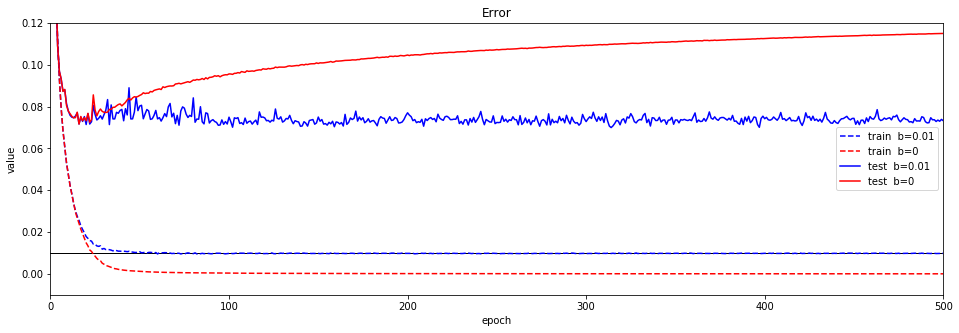
テストデータの正解率は、精度が向上している場合もありますが、乱高下を繰り返していることには変わりはありません。
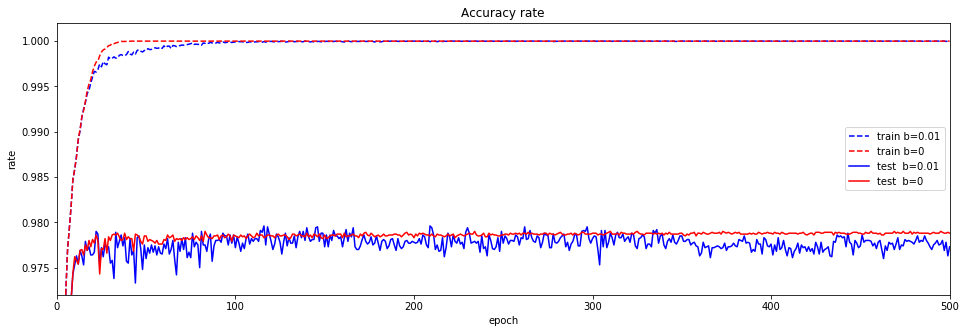
bの変更
$ b $を0.001~0.1まで変更して確認します。500エポック実行しています。
まずは、精度の表です。
|活性化関数|学習正解|テスト正解|テスト最高|
|-----|----:|----:|----:|----:|----:|----:|
|b=0 | 100.00 | 97.85 | 97.88 |
|b=0.1 | 98.69 | 97.21 | 98.05 |
|b=0.05 | 99.26 | 97.67 | 98.01 |
|b=0.01 | 99.90 | 97.60 | 97.90 |
|b=0.005 | 99.99 | 97.77 | 97.93 |
|b=0.001 | 100.00 | 97.83 | 97.94 |
どう判断してよいかわからないですね。グラフで見てみます。
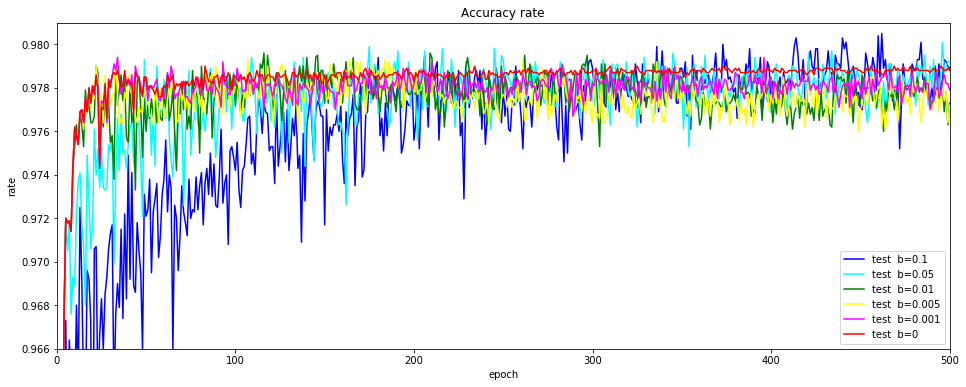
学習データの誤差です。$ b $の値に収束していますね。

テストデータの誤差です。上下していますが、Floodingありの場合の過学習の度合いが小さいようです。
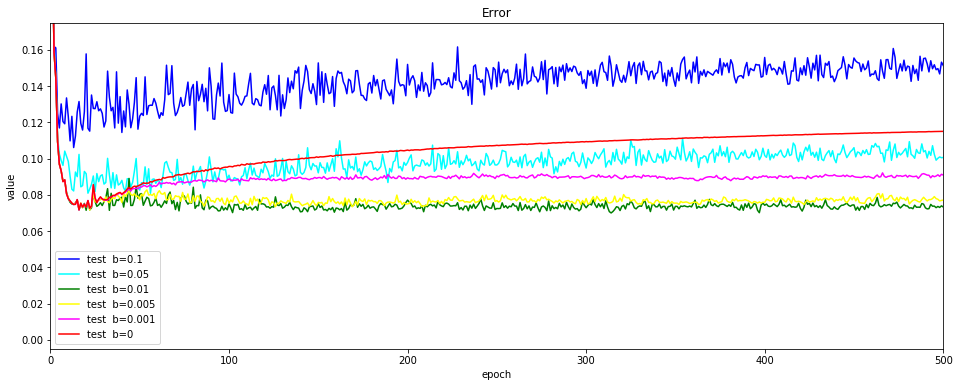
正解率の推移です。まずは、学習データ、$ b $の値が大きくなるにつれて精度が徐々に向上していますが、最終的には100%に近づきます。
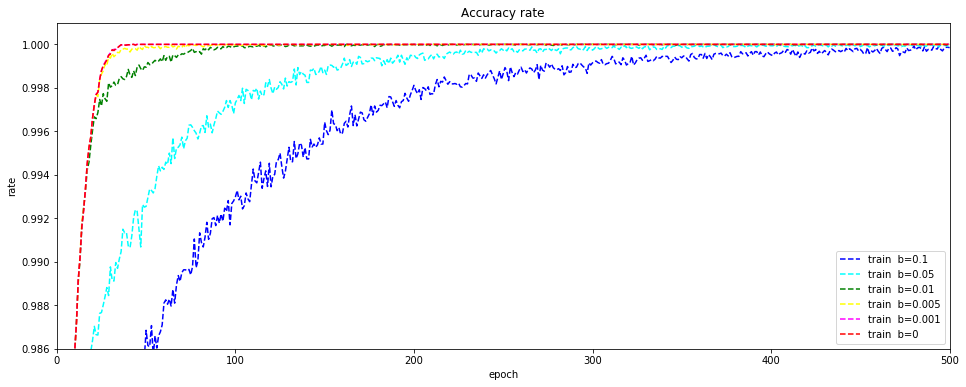
テストデータの正解率です。学習データ同様に、$ b $の値が大きくなるにつれて精度の向上が遅いです。ただし、最終的には、より良い精度が出る場合もあります。
Floodingにより確かに精度が向上する場合があることはわかりました。ただし、乱高下するなか精度の良いポイントを見つけるのは難しいし、また、エポック数が多くなり学習に時間がかかります。
私の理解不足により、考え方や実装に不備があるかもしれませんが、今回の結果からは、ドロップアウトや重み減衰などのほかの正則化の手法を使った方が安定して精度が良くなりそうです。
Nesterovの加速勾配法
以前には、オプティマイザとして、Nesterovに対応していたのですが、実装変更により未対応になりました。ここで実装してみます。
まずは、Nestetovの復習です。ディープラーニングを実装から学ぶ(6-2)学習手法(最適化) Nesterovの加速勾配法に記載しております。
基本的には、Momentumと同じですが、勾配を計算する位置が異なります。
\begin{align}
v_{k+1} &= \mu v_k - \eta E^{'}(w_k + \mu v_k), v_0 = 0\\
w_{k+1} &= w_k + v_{k+1}
\end{align}
学習前に重みを更新し、更新した重みで学習する必要があります。事前に重みを更新する必要があるため単純にフレームワークに組み込めませんでした。
事前に重みを更新せず代替えする方法があるようなのでこちらを試みます。
式です。
\begin{align}
v_{k+1} &= \mu v_k - \eta E^{'}(w_k), v_0 = 0\\
w_{k+1} &= w_k - \mu v_k + \mu v_{k+1} + v_{k+1}
\end{align}
実装です。基本的にそのまま実装しています。
def Nesterov(W, dW, lr=0.01, mu=0.9, v=None):
if v is None:
v = np.zeros_like(W)
v_1 = mu * v - lr * dW
return W - mu * v + mu * v_1 + v_1, {"v":v_1}
実行
データの読み込みは、上と同じため省略します。
モデル定義
オプティマイザにNesterovを設定します。
model = create_model(nx_train.shape[1]) # 28*28
model = add_layer(model, "affine1", affine, 100)
model = add_layer(model, "relu1", relu)
model = add_layer(model, "affine2", affine, 50)
model = add_layer(model, "relu2", relu)
model = add_layer(model, "affine3", affine, 10)
model = set_output(model, softmax)
model = set_error(model, cross_entropy_error)
optimizer = create_optimizer(Nesterov, lr=0.1, mu=0.9)
実行
epoch = 50
batch_size = 100
np.random.seed(10)
model, optimizer, learn_info = learn(model, nx_train, t_train, nx_test, t_test, batch_size=batch_size, epoch=epoch, optimizer=optimizer)
結果
input - 0 784
affine1 affine 784 100
relu1 relu 100 100
affine2 affine 100 50
relu2 relu 50 50
affine3 affine 50 10
output softmax 10
error cross_entropy_error
0 0.08133333333333333 2.489248983149533 0.0838 2.490209670597171
1 0.9200833333333334 0.26186500840062027 0.9535 0.1514170563101203
2 0.9637 0.11914309912655469 0.9654 0.11231315698876188
3 0.9718333333333333 0.09248191282197123 0.9682 0.10823139592056166
4 0.9764333333333334 0.07685608288520128 0.9714 0.09902091457935464
5 0.97905 0.06712863476957766 0.9706 0.0993606464749246
6 0.9817833333333333 0.058173787576293406 0.9698 0.10377889761320552
7 0.9832333333333333 0.0533021405978163 0.9711 0.10104197454481403
8 0.9854833333333334 0.046687690372713066 0.9725 0.10561961552095166
9 0.9868 0.039634233130594616 0.9683 0.12742158757594688
10 0.98805 0.03904980918739183 0.9747 0.09805639356407904
11 0.9874333333333334 0.03957846083639053 0.9761 0.09721253704664258
12 0.9899166666666667 0.031455008198849124 0.9753 0.10639151530472002
13 0.9899 0.032186353485254234 0.9744 0.10967274133525516
14 0.9895666666666667 0.03145523152870706 0.9754 0.1140907048219793
15 0.9915166666666667 0.02752904162481483 0.9765 0.12073982915669737
16 0.9911833333333333 0.028033280231723315 0.9752 0.11072339109298428
17 0.9908666666666667 0.030566558741910797 0.9735 0.1319468935283732
18 0.9914333333333334 0.028131809984440512 0.9745 0.12495158067053919
19 0.9919666666666667 0.026150828131463306 0.9716 0.14607558487562863
20 0.9916333333333334 0.028123900548652284 0.9747 0.1279127330162319
21 0.9921333333333333 0.025214382904283298 0.9764 0.12686086870257576
22 0.9917166666666667 0.027334474558396053 0.9772 0.12735385078138187
23 0.9922833333333333 0.02592413555230186 0.9758 0.13446031243595852
24 0.9939166666666667 0.020727617912274406 0.9734 0.14651961151730306
25 0.9939 0.019762689151932362 0.9764 0.12269843236453346
26 0.9947166666666667 0.01668373966694252 0.9753 0.14759081682648736
27 0.9938333333333333 0.022361984094279596 0.9755 0.14080167011578013
28 0.9942 0.019461844248101844 0.9714 0.1605328226876979
29 0.9939666666666667 0.02160156738266948 0.9735 0.16052290322040713
30 0.9933333333333333 0.022987548729107365 0.9722 0.15898013023363167
31 0.9932666666666666 0.02394940719623612 0.9777 0.13656645776419638
32 0.99445 0.01994391168799906 0.9725 0.16615641009421753
33 0.9920333333333333 0.02941828128703869 0.9741 0.16033036598507105
34 0.9946 0.019530274770593364 0.9751 0.1609551149225599
35 0.9929666666666667 0.025621001752724065 0.9722 0.18414786068735864
36 0.9938166666666667 0.02213717269949415 0.9727 0.17562965997405391
37 0.9932333333333333 0.02734410084357933 0.9764 0.15322870030408747
38 0.9955666666666667 0.015479363645790958 0.9755 0.15670002042151246
39 0.9944166666666666 0.0218263212044709 0.9732 0.17975173318842158
40 0.9949333333333333 0.017919558239593847 0.9793 0.1447865959334684
41 0.99665 0.011601428289041985 0.974 0.1923008639997574
42 0.9942333333333333 0.02132315781879206 0.977 0.16357686697968216
43 0.9933 0.02734671036059377 0.9738 0.18425573658262007
44 0.9939333333333333 0.02302265355783376 0.9688 0.20645978004638332
45 0.9929833333333333 0.025031169354017682 0.9745 0.18092019370658774
46 0.99335 0.026484824538483963 0.9749 0.18964369747289855
47 0.9943 0.024120190153847282 0.9714 0.21111486590152687
48 0.9934666666666667 0.02675135419380716 0.9743 0.18886474931434874
49 0.9938833333333333 0.024959160695263535 0.9753 0.18400409120934202
50 0.9940833333333333 0.02317647954026353 0.9731 0.21149020562045284
所要時間 = 1 分 15 秒
比較
基本の実行
SGD,Momentumと比較します。$ \mu $は、既定値の0.9です。
| オプティマイザ | 学習正解 | テスト正解 | テスト最高 | TS95% | TS97% | TS98% |
|---|---|---|---|---|---|---|
| SGD | 100.00 | 97.85 | 97.88 | 2 | 5 | - |
| Momentum | 99.52 | 96.97 | 97.86 | 2 | 5 | - |
| Nesterov | 99.41 | 97.31 | 97.93 | 1 | 4 | - |
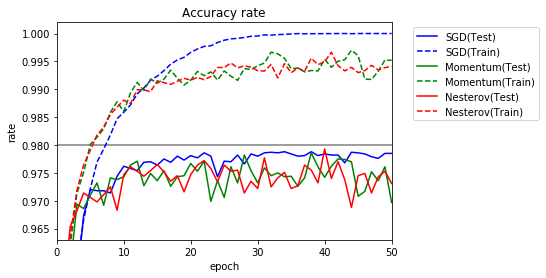
テストの正解率が乱高下しています。慣性の法則を利用しているため、同じ方向に更新される場合に重みが大きく更新されてしまう影響もあると考えられます。
lr=0.01
学習係数を小さくしてみましょう。lr=0.01の場合です。
| オプティマイザ | 学習率 | 学習正解 | テスト正解 | テスト最高 | TS95% | TS97% | TS98% |
|---|---|---|---|---|---|---|---|
| SGD | 0.1 | 100.00 | 97.85 | 97.88 | 2 | 5 | - |
| Momentum | 0.01 | 100.00 | 98.05 | 98.10 | 2 | 6 | 31 |
| Nesterov | 0.01 | 100.00 | 98.07 | 98.10 | 2 | 6 | 27 |
精度が良くなりました。学習係数の調整が必要です。
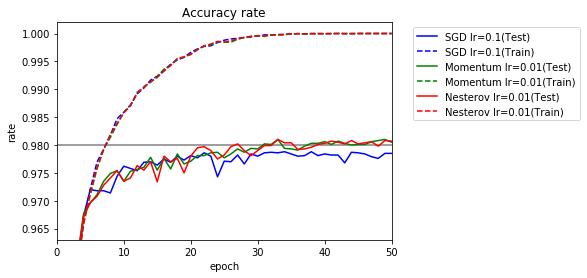
μ変更
$ \mu $を0.9~0.5まで変更してみます。学習率は、0.1です。
Momentumと比較します。
| オプティマイザ | $ \mu $ | 学習正解 | テスト正解 | テスト最高 |
|---|---|---|---|---|
| SGD | - | 100.00 | 97.85 | 97.88 |
| Momentum | 0.9 | 99.52 | 96.97 | 97.86 |
| Momentum | 0.8 | 100.00 | 98.19 | 98.20 |
| Momentum | 0.7 | 100.00 | 98.18 | 98.22 |
| Momentum | 0.6 | 100.00 | 97.99 | 98.10 |
| Momentum | 0.5 | 100.00 | 97.94 | 98.02 |
| Nesterov | 0.9 | 99.41 | 97.31 | 97.93 |
| Nesterov | 0.8 | 100.00 | 98.13 | 98.15 |
| Nesterov | 0.7 | 100.00 | 97.84 | 97.86 |
| Nesterov | 0.6 | 100.00 | 97.97 | 98.01 |
| Nesterov | 0.5 | 100.00 | 98.03 | 98.09 |
Momentumと比較すると微妙ですね。$ \mu $をうまく調整すればSGDよりは精度が向上します。
ここでひとつお断りです。
ディープラーニングを実装から学ぶ(6-2)学習手法(最適化) Nesterovの加速勾配法の実装に一部間違いがありました。
本来は、重み更新時には、勾配計算時の変更した重み($ w_k + \mu v_k $)ではなく、元の重み($ w_k $)を利用する必要がありました。今回の結果が正しいです。
まとめ
活性化関数は、特に性能にこだわりがない場合は、$ \mathrm{tanhexp} $を試す価値はあると思います。
Floodingは、精度が高くなる場合もありましたが乱高下するため、どこで学習を終了するかが難しいです。私の理解が足りていないのか、正則化はドロップアウトでよいのではないでしょうか、
Nesterovは、学習係数または$ \mu $をうまく調整できれば使えそうです。