今回は、重みの更新の最適化手法について実装してみます。データは、引き続きMNISTです。手法として、Momentum、Nestrovの加速勾配法、AdaGrad、RMSProp、Adadelta、Adamを試してみます。
SGD
今まで、重み、バイアスの更新は、勾配に学習率($ \eta $)を掛けて計算していました。
w_{k+1} = w_k - \eta E^{'}(w_k)
学習率が大きいと、序盤は早く学習が進みますが、後半はなかなか収束しません。逆に、学習率が小さいと学習が進みません。よって、学習率を徐々に小さくするとよいと考えられます。
重みの学習率をエポック数で割ってみます。
# 重み、バイアスの調整
for k in range(1, layer+1):
W[k] = W[k] - eta*dW[k]/(i+1)
b[k] = b[k] - eta*db[k]/(i+1)
また、エポックの平方根で割った場合も試してみます。
# 重み、バイアスの調整
for k in range(1, layer+1):
W[k] = W[k] - eta*dW[k]/np.sqrt(i+1)
b[k] = b[k] - eta*db[k]/np.sqrt(i+1)
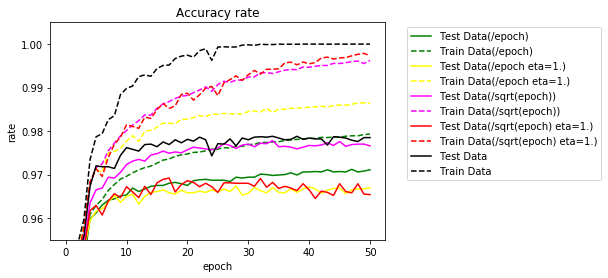
学習率を0.1と1.0で試してみました。50エポック実行時の結果です。
- 学習正解:50エポック実行後の学習データの正解率(%)
- テスト正解:50エポック実行後のテストデータの正解率(%)
- TS95%:テストデータの正解率が95%に達したエポック数
- TS97%:テストデータの正解率が97%に達したエポック数
- TS98%:テストデータの正解率が98%に達したエポック数
- TS最高:テストデータの最高正解率(%)
- エポック:テストデータの最高正解率時のエポック数
| 倍率 | 学習率 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|---|
| 1/エポック | 0.1 | 97.93 | 97.11 | 3 | 32 | - | 97.12 | 47 |
| 1/エポック | 1.0 | 98.64 | 96.70 | 3 | - | - | 96.73 | 28 |
| 1/$ \sqrt{エポック} $ | 0.1 | 99.63 | 97.66 | 2 | 9 | - | 97.78 | 34 |
| 1/$ \sqrt{エポック} $ | 1.0 | 99.73 | 96.54 | 3 | - | - | 96.92 | 17 |
| 1(参考) | 0.1 | 100.00 | 97.85 | 2 | 5 | - | 97.88 | 34 |
エポックの平方根で割った場合、まずまずの結果でした。
実装
最適化の各手法をサポートするために、重みの更新を関数化します。パラメータ、戻り値を以下のようにします。
def optimizer(W, dW, optimizer_params, optimizer_stats):
return newW, optimizer_stats
SGDは、以下とします。
def SGD(W, dW, eta, optimizer_params, optimizer_stats):
return W - eta*dW, optimizer_stats
学習のパラメータに最適化関連のパラメータを追加します。変更部分を示します。
optimizer_func=SGD, # 最適化関数
optimizer_params={}, # 最適化パラメータ
# 最適化情報初期化
optimizer_statsW = {}
optimizer_statsb = {}
for i in range(layer):
optimizer_statsW[i+1] = {}
optimizer_statsb[i+1] = {}
# 重み、バイアスの調整
for k in range(1, layer+1):
#W[k] = W[k] - eta*dW[k]
#b[k] = b[k] - eta*db[k]
W[k], optimizer_statsW[k] = optimizer_func(W[k], dW[k], eta, optimizer_params, optimizer_statsW[k])
b[k], optimizer_statsb[k] = optimizer_func(b[k], db[k], eta, optimizer_params, optimizer_statsb[k])
更新量
重みの更新部分を$ v $とするとSDGは、以下で表せます。
\begin{align}
v_{k+1} &= -\eta E^{'}(w_k)\\
w_{k+1} &= w_k + v_{k+1}
\end{align}
Momentum
Momentumは、過去の更新分に$ \mu $を掛けた分を加えて更新します。$ \mu $は、0.5~0.9程度の値を利用するようです。
\begin{align}
v_{k+1} &= \mu v_k - \eta E^{'}(w_k), v_0 = 0\\
w_{k+1} &= w_k + v_{k+1}
\end{align}
更新量は、一般に以下のようになります。過去の更新分をすべて足し合わせます。ただし、$ \mu $は1より小さい値を設定するため、過去になればなるほど影響が小さくなります。
\begin{align}
v_0 &= 0\\
v_1 &= \mu * 0 - \eta E^{'}(w_0)\\
&= -\eta (E^{'}(w_0))\\
v_2 &= \mu * (- \eta E^{'}(w_0)) - \eta E^{'}(w_1)\\
&= -\eta (\mu E^{'}(w_0) + E^{'}(w_1))\\
v_3 &= \mu(-\eta (\mu E^{'}(w_0) + E^{'}(w_1))) - \eta E^{'}(w_2)\\
&= -\eta (\mu^2 E^{'}(w_0) + \mu E^{'}(w_1) + E^{'}(w_2))\\
\cdots\\
v_{k+1} &= -\eta (\mu^k E^{'}(w_0) + \mu^{k-1} E^{'}(w_1) + \cdots + \mu E^{'}(w_{k-1}) + E^{'}(w_k))
\end{align}
まとめると、
v_{k+1} = -\eta \sum_{s=0}^{k}\mu^{k-s} E^{'}(w_s)
ひとつ前の更新量が正だとすると、今回の更新量が正であれば、より大きく正の方向に更新されます。逆に、負だと、今回の更新量からマイナスされるため、更新量が小さくなります。同じ方向であれば、大きく更新、逆の方向であれば、小さく更新することになります。
実装
初期値として、0を設定します。vの値は、optimizer_statsに保持しておきます。$ \mu $は、optimizer_paramsに"mu"として設定します。
def Momentum(W, dW, eta, optimizer_params, optimizer_stats):
if "v" not in optimizer_stats: # vの初期値設定
optimizer_stats["v"] = np.zeros_like(W)
# vの更新
optimizer_stats["v"] = optimizer_params["mu"] * optimizer_stats["v"] - eta * dW
return W + optimizer_stats["v"], optimizer_stats
実行
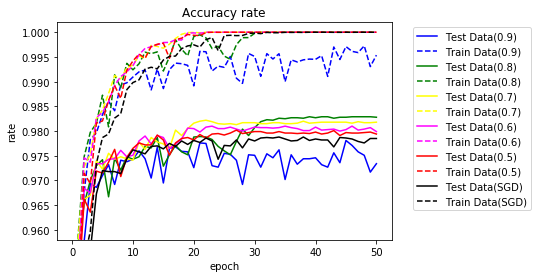
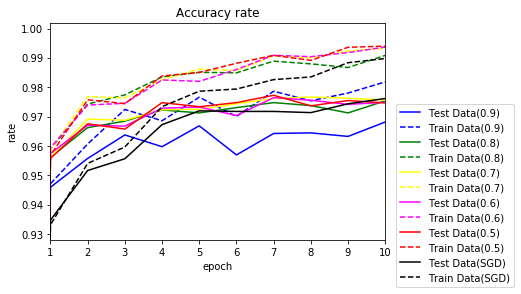
$ \mu $を0.5~0.9で実行してみます。
| $ \mu $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.9 | 99.54 | 97.34 | 2 | 5 | - | 97.81 | 45 |
| 0.8 | 100.00 | 98.28 | 1 | 3 | 28 | 98.29 | 39 |
| 0.7 | 100.00 | 98.18 | 1 | 4 | 17 | 98.22 | 22 |
| 0.6 | 100.00 | 97.99 | 1 | 4 | 19 | 98.10 | 23 |
| 0.5 | 100.00 | 97.94 | 2 | 4 | 27 | 98.02 | 27 |
| SGD | 100.00 | 97.85 | 2 | 5 | - | 97.88 | 34 |
$ \mu $を0.5~0.8に設定した場合、Momentumを適用した場合、よい結果が得られることがわかりました。
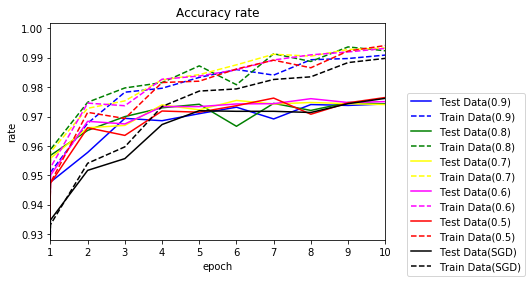
10エポックまでを拡大してみます。
特に、Momentumを適用した場合、黒のSGDに比べて、序盤に学習が早く進んでいることがわかります。
学習率を0.01で実行してみます。
| $ \mu $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.9 | 100.00 | 98.05 | 2 | 6 | 31 | 98.10 | 33 |
| 0.8 | 99.97 | 97.70 | 4 | 10 | - | 97.81 | 23 |
| 0.7 | 99.84 | 97.66 | 6 | 14 | - | 97.76 | 45 |
| 0.6 | 99.57 | 97.62 | 7 | 19 | - | 97.71 | 45 |
| 0.5 | 99.32 | 97.55 | 7 | 23 | - | 97.66 | 45 |
今度は、$ \mu $が0.9の場合が最高でした。$ \mu $の値はケースバイケースで試してみるしかないようです。
次に、バッチサイズを変更してみます。学習率0.1、$ \mu = 0.8 $の場合です。
| バッチサイズ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 10 | 19.05 | 19.40 | - | - | - | 89.90 | 2 |
| 100 | 100.00 | 98.28 | 1 | 3 | 28 | 98.29 | 39 |
| 1000 | 99.96 | 97.82 | 5 | 11 | - | 97.88 | 42 |
バッチサイズの影響も大きいことがわかりました。
Nesterovの加速勾配法
Momentumと同じですが、勾配を計算する位置が異なります。次の値が$ w_k + \mu v_k $になるだろうと想定し、勾配を計算します。
\begin{align}
v_{k+1} &= \mu v_k - \eta E^{'}(w_k + \mu v_k), v_0 = 0\\
w_{k+1} &= w_k + v_{k+1}
\end{align}
実装
Nesterovの実装は、Momentumと同じです。
def Nesterov(W, dW, eta, optimizer_params, optimizer_stats):
if "v" not in optimizer_stats:
optimizer_stats["v"] = np.zeros_like(W)
optimizer_stats["v"] = optimizer_params["mu"] * optimizer_stats["v"] - eta * dW
return W + optimizer_stats["v"], optimizer_stats
順伝播、逆伝播の計算の前に、重み、バイアスを$ w_k + \mu v_k $に変更します。
# Nesterov
if optimizer_func == Nesterov:
for k in range(1, layer+1):
if "v" in optimizer_statsW[k]:
W[k] = W[k] + optimizer_params["mu"] * optimizer_statsW[k]["v"]
if "v" in optimizer_statsb[k]:
b[k] = b[k] + optimizer_params["mu"] * optimizer_statsb[k]["v"]
実行
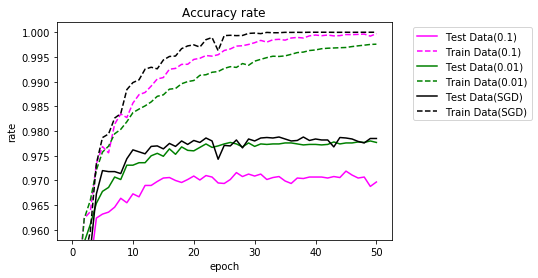
$ \mu $を0.5~0.9に変更し実行してみます。0.8~0.5でSGDを上回りました。
| $ \mu $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.9 | 97.96 | 96.41 | 2 | 20 | - | 97.19 | 33 |
| 0.8 | 99.86 | 97.92 | 1 | 4 | 14 | 98.03 | 49 |
| 0.7 | 100.00 | 98.23 | 1 | 4 | 30 | 98.27 | 48 |
| 0.6 | 100.00 | 98.23 | 1 | 4 | 19 | 98.23 | 50 |
| 0.5 | 100.00 | 98.03 | 1 | 4 | 19 | 98.07 | 27 |
| SGD | 100.00 | 97.85 | 2 | 5 | - | 97.88 | 34 |
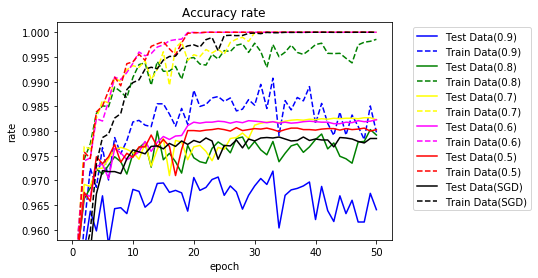
50エポックまでのグラフです。
10エポックまで拡大します。
Momentumとどちらが良いかは微妙です。
AdaGrad
今までは、学習率はすべての重みに対して$ \eta $ひとつでした。ここからは、$ \eta $を重みごとに変更します。
以下の式で表します。
\begin{align}
g_{k+1} &= g_k + (E^{'}(w_k))^2, g_0 = 0\\
w_{k+1} &= w_k - \frac{\eta}{\sqrt{g_{k+1}}} E^{'}(w_k)
\end{align}
学習率が$ \frac{\eta}{\sqrt{g_{k+1}}} $と言えます。
$ g $の詳細を確認してみましょう。
\begin{align}
g_0 &= 0\\
g_1 &= g_0 + (E^{'}(w_0))^2\\
&= (E^{'}(w_0))^2\\
g_2 &= g_1 + (E^{'}(w_1))^2\\
&= (E^{'}(w_0))^2 + (E^{'}(w_1))^2\\
g_3 &= g_2 + (E^{'}(w_2))^2\\
&= (E^{'}(w_0))^2 + (E^{'}(w_1))^2 + (E^{'}(w_2))^2\\
\cdots\\
g_{k+1} &= (E^{'}(w_0))^2 + (E^{'}(w_1))^2 + \cdots + (E^{'}(w_k))^2
\end{align}
まとめると、
g_{k+1} = \sum_{s=0}^{k}(E^{'}(w_s))^2
単に重みを順に2乗して加えているだけです。単純増加になります。
実装
実装は、以下の通り
def AdaGrad(W, dW, eta, optimizer_params, optimizer_stats):
if "g" not in optimizer_stats:
optimizer_stats["g"] = np.zeros_like(W)
optimizer_stats["g"] = optimizer_stats["g"] + (dW * dW)
return W - (eta * dW)/np.sqrt(np.maximum(optimizer_stats["g"], 1e-7)), optimizer_stats
実行
学習率を変更しながら実行してみました。
| 学習率 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.1 | 99.97 | 96.97 | 2 | 15 | - | 97.19 | 45 |
| 0.01 | 99.76 | 97.77 | 2 | 7 | - | 97.80 | 49 |
| 0.001 | 94.93 | 94.83 | - | - | - | 94.83 | 50 |
| SGD | 100.00 | 97.85 | 2 | 5 | - | 97.88 | 34 |
SGDは、超えませんでした。
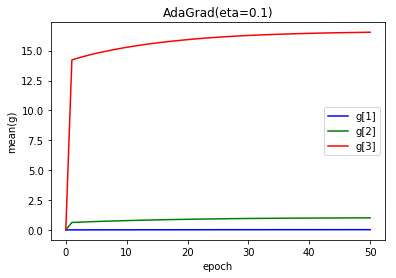
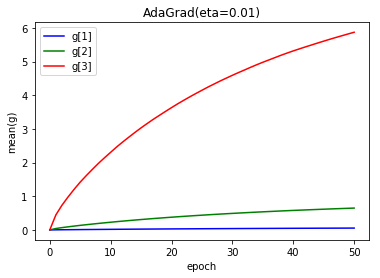
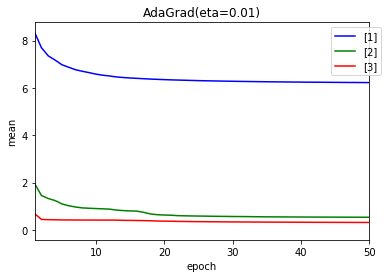
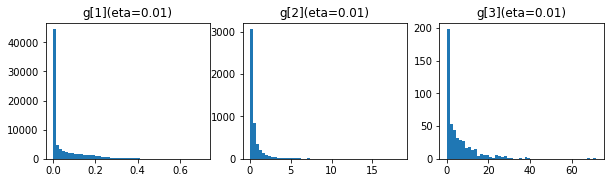
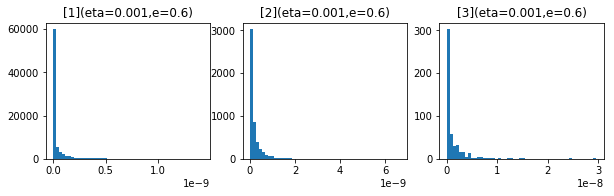
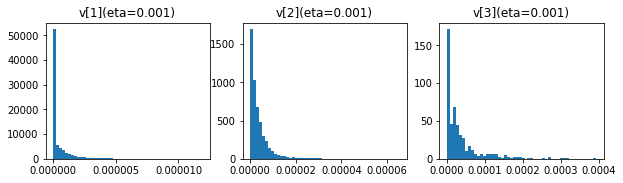
$ g $および、学習率に相当する$ \frac{\eta}{\sqrt{g}} $の値の変化をエポック終了ごとに見てみましょう。値は、$ g $および$ \frac{\eta}{\sqrt{g}} $の平均値です。
- 学習率 0.1
上のグラフが$ g $、下が、$ \frac{\eta}{\sqrt{g}} $です。
1エポック目で大きな値となり、結果、学習率が小さくなり学習が進まなくなったと考えられます。
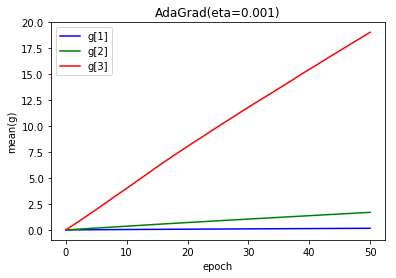
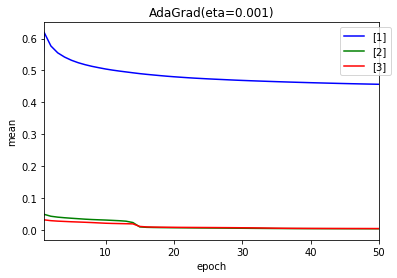
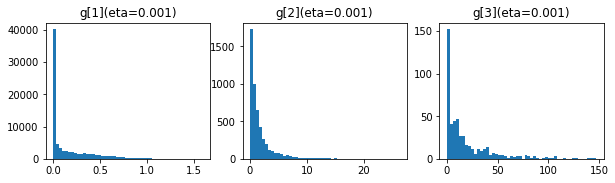
- 学習率 0.01
- 学習率 0.001
順調に大きな値になっていますが、もともとの学習率が小さいため学習が進みませんでした。
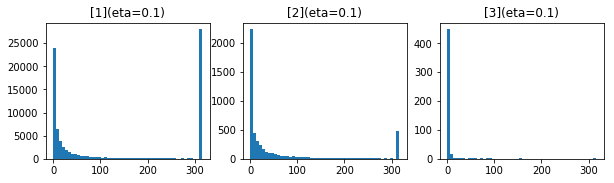
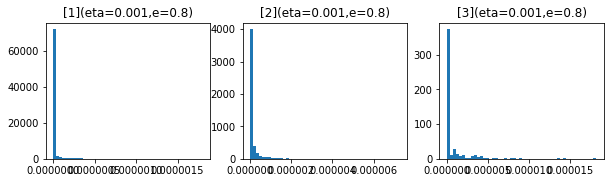
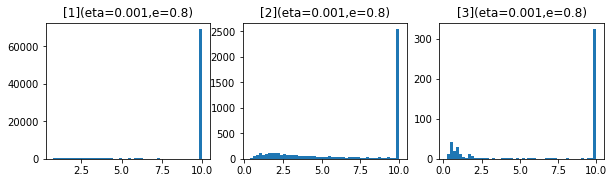
50エポック後の$ g $、$ \frac{\eta}{\sqrt{g}} $の値の分布です。
- 学習率 0.1
上のグラフが$ g $、下が、$ \frac{\eta}{\sqrt{g}} $です。
- 学習率 0.01
- 学習率 0.001
どうも重みの初期値への依存が大きいようです。重みの初期値を生成する乱数のseed値を変更し、3回実行してみました。学習率は、0.1です。
| seed | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| A | 100.00 | 97.36 | 1 | 6 | - | 97.52 | 11 |
| B | 100.00 | 96.83 | 1 | 12 | - | 97.11 | 12 |
| C | 100.00 | 97.04 | 1 | 5 | - | 97.32 | 11 |
SGDの場合です。同じ重みの初期値で試してみます。
| seed | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| A | 100.00 | 97.93 | 2 | 6 | - | 97.93 | 25 |
| B | 100.00 | 97.96 | 2 | 6 | - | 98.03 | 32 |
| C | 100.00 | 97.80 | 2 | 6 | - | 97.91 | 26 |
たまたまかもしれませんが、AdaGradの方が重みの初期値に敏感なように思われます。
バッチサイズの確認です。学習率は、0.01です。
| バッチサイズ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 10 | 99.77 | 97.76 | 1 | 5 | - | 97.78 | 45 |
| 100 | 99.76 | 97.77 | 2 | 7 | - | 97.80 | 49 |
| 1000 | 99.23 | 97.59 | 4 | 20 | - | 97.60 | 45 |
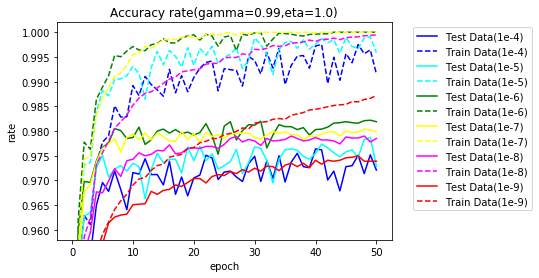
最後に、実装上0の平方根とならないように最小値を1e-7に是正しています。$ g $が0となるケースも多いようなので、是正する値を変更して試してみます。
| $ \varepsilon $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 1e-4 | 99.91 | 96.70 | 2 | 15 | - | 97.05 | 15 |
| 1e-5 | 99.98 | 96.97 | 1 | 8 | - | 97.29 | 8 |
| 1e-6 | 99.98 | 96.94 | 2 | 13 | - | 97.12 | 16 |
| 1e-7 | 99.97 | 96.97 | 2 | 15 | - | 97.19 | 45 |
| 1e-8 | 99.99 | 96.77 | 2 | - | - | 96.87 | 15 |
| 1e-9 | 99.95 | 96.70 | 2 | - | - | 96.87 | 15 |
値によって、結果がかなり違いました。パラメータにした方がよいのか?
AdaGrad自体には、パラメータはありませんが、学習率や重みの初期値などパラメータの調整が大変そうです。
RMSProp
AdaGradが勾配の2乗をすべて加えていくため、一旦、値が大きくなると学習が進まなくなります。
RMSPropは、その点を改良したものです。
\begin{align}
g_{k+1} &= \gamma g_k + (1 - \gamma)(E^{'}(w_k))^2, g_0 = 0\\
w_{k+1} &= w_k - \frac{\eta}{\sqrt{g_{k+1}}} E^{'}(w_k)
\end{align}
$ g $の詳細を確認してみましょう。
\begin{align}
g_0 &= 0\\
g_1 &= \gamma g_0 + (1 - \gamma)(E^{'}(w_0))^2\\
&= (1 - \gamma)(E^{'}(w_0))^2\\
g_2 &= \gamma g_1 + (1 - \gamma)(E^{'}(w_1))^2\\
&= \gamma (1 - \gamma)(E^{'}(w_0))^2 + (1 - \gamma)(E^{'}(w_1))^2\\
g_3 &= \gamma g_2 + (1 - \gamma)(E^{'}(w_2))^2\\
&= \gamma^2 (1 - \gamma)(E^{'}(w_0))^2 + \gamma (1 - \gamma)(E^{'}(w_1))^2 + (1 - \gamma)(E^{'}(w_2))^2\\
\cdots\\
g_{k+1} &= \gamma^k (1 - \gamma)(E^{'}(w_0))^2 + \gamma^{k-1} (1 - \gamma)(E^{'}(w_1))^2 + \cdots + (1 - \gamma)(E^{'}(w_{k}))^2
\end{align}
まとめると、
g_{k+1} = (1 - \gamma)\sum_{s=0}^{k}\gamma^{k-s}(E^{'}(w_s))^2
$ \gamma $は、1未満を設定するため、過去のデータの影響が徐々に小さくなります。
実装
実装は、以下の通り
def RMSProp(W, dW, eta, optimizer_params, optimizer_stats):
if "g" not in optimizer_stats:
optimizer_stats["g"] = np.zeros_like(W)
optimizer_stats["g"] = optimizer_params["gamma"] * optimizer_stats["g"] + (1 - optimizer_params["gamma"]) * dW * dW
return W - (eta * dW)/np.sqrt(np.maximum(optimizer_stats["g"], 1e-7)), optimizer_stats
実行
$ \gamma $を0.99,0.9~0.5に変更しながら試してみます。
- 学習率 0.1
全く学習が進みませんでした。$ 1 - \gamma $を掛けていることが影響しているのか、
| $ \gamma $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.99 | 20.32 | 20.62 | - | - | - | 44.28 | 1 |
| 0.9 | 36.55 | 36.03 | - | - | - | 60.31 | 2 |
| 0.8 | 37.91 | 37.36 | - | - | - | 68.32 | 3 |
| 0.7 | 59.82 | 59.58 | - | - | - | 79.81 | 8 |
| 0.6 | 62.08 | 61.98 | - | - | - | 85.17 | 2 |
| 0.5 | 16.76 | 16.96 | - | - | - | 30.86 | 15 |
| SGD | 100.00 | 97.85 | 2 | 5 | - | 97.88 | 34 |
- 学習率 0.01
| $ \gamma $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.99 | 98.72 | 96.50 | 2 | - | - | 96.50 | 50 |
| 0.9 | 98.76 | 96.79 | 1 | 36 | - | 97.22 | 36 |
| 0.8 | 98.11 | 95.98 | 1 | - | - | 96.90 | 26 |
| 0.7 | 98.93 | 97.05 | 1 | 22 | - | 97.53 | 35 |
| 0.6 | 99.06 | 97.13 | 1 | 28 | - | 97.31 | 49 |
| 0.5 | 98.43 | 96.85 | 1 | 32 | - | 97.22 | 42 |
| SGD | 98.08 | 97.08 | 15 | 44 | - | 97.17 | 48 |
- 学習率 0.001
| $ \gamma $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.99 | 99.94 | 97.88 | 2 | 4 | - | 97.95 | 25 |
| 0.9 | 100.00 | 97.91 | 2 | 4 | - | 97.96 | 45 |
| 0.8 | 100.00 | 97.99 | 2 | 4 | 43 | 98.03 | 43 |
| 0.7 | 100.00 | 97.96 | 2 | 4 | - | 97.99 | 49 |
| 0.6 | 100.00 | 97.89 | 2 | 4 | - | 97.93 | 17 |
| 0.5 | 99.98 | 97.83 | - | - | - | 97.88 | 17 |
| SGD | 92.05 | 92.37 | 2 | 4 | - | 97.81 | 45 |
- 学習率 0.0001
| $ \gamma $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.99 | 99.54 | 97.77 | 7 | 19 | - | 97.81 | 45 |
| 0.9 | 99.16 | 97.68 | 8 | 24 | - | 97.72 | 48 |
| 0.8 | 99.00 | 97.63 | 8 | 25 | - | 97.63 | 50 |
| 0.7 | 98.89 | 97.65 | 9 | 25 | - | 97.66 | 45 |
| 0.6 | 98.80 | 97.58 | 9 | 27 | - | 97.62 | 45 |
| 0.5 | 98.72 | 97.58 | 10 | 27 | - | 97.58 | 50 |
| SGD | 78.69 | 79.22 | - | - | - | 79.22 | 50 |
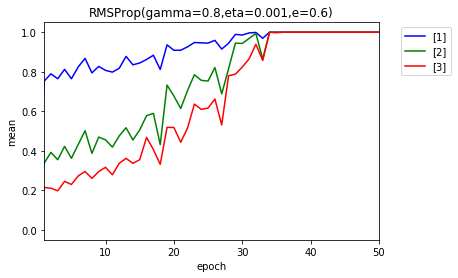
学習率が0.001の場合のグラフです。SGDの学習率は、0.1です。
AdaGradと同様に、$ g $および、学習率に相当する$ \frac{\eta}{\sqrt{g}} $の値の変化をエポック終了ごとに見てみましょう。値は、$ g $および$ \frac{\eta}{\sqrt{g}} $の平均値です。
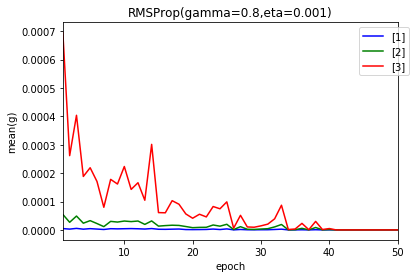
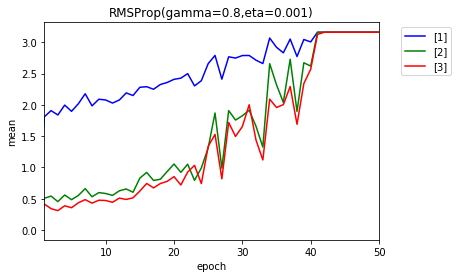
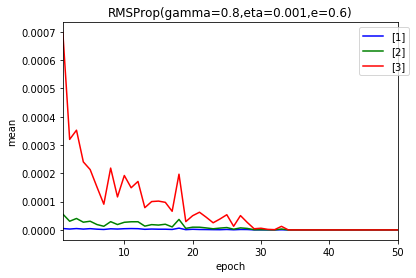
結果の一番良かった、学習率 0.001、$ \gamma $ = 0.8の場合です。
上のグラフが$ g $、下が、$ \frac{\eta}{\sqrt{g}} $です。
AdaGradと違い、$ g $は、減少しています。ただ、$ g $は、かなり小さい値になりました。40エポック目以降は、ほとんど0です。
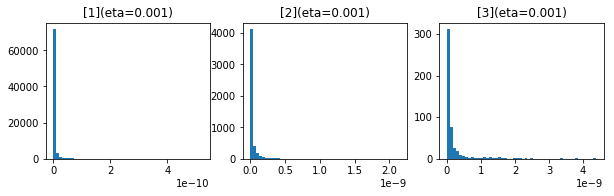
50エポック後の$ g $および$ \frac{\eta}{\sqrt{g}} $の分布です。
上のグラフが$ g $、下が、$ \frac{\eta}{\sqrt{g}} $です。
やはり、ほとんど0になっています。
平方根がエラーとならないように最小値を1e-7に是正していますが、ほとんど0なので影響がありそうです。
値を変更して試してみます。
| $ \varepsilon $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 1e-4 | 100.00 | 97.91 | 3 | 7 | 22 | 98.00 | 22 |
| 1e-5 | 100.00 | 97.81 | 2 | 6 | - | 97.99 | 28 |
| 1e-6 | 100.00 | 98.06 | 2 | 4 | 34 | 98.09 | 45 |
| 1e-7 | 100.00 | 97.99 | 2 | 4 | 43 | 98.03 | 43 |
| 1e-8 | 100.00 | 97.93 | 2 | 4 | 22 | 98.09 | 22 |
| 1e-9 | 99.99 | 97.80 | 2 | 4 | - | 97.98 | 12 |
グラフ化します。
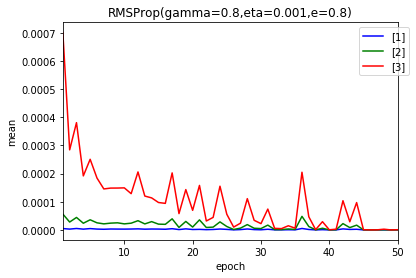
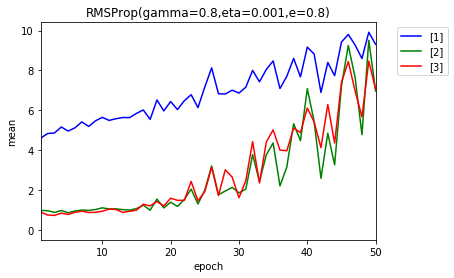
1e-6、1e-7、1e-8の場合の$ g $および$ \frac{\eta}{\sqrt{g}} $の平均値です。
上のグラフが$ g $、下が、$ \frac{\eta}{\sqrt{g}} $です。
- 1e-6
- 1e-7
- 1e-8
50エポック後の$ g $および$ \frac{\eta}{\sqrt{g}} $の分布です。
- 1e-6
- 1e-7
- 1e-8
やはり、影響しているようです。パラメータを考えます。
バッチサイズの変更を試します。学習率 0.001、$ \gamma $ = 0.8の場合です。
| バッチサイズ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 10 | 99.62 | 97.40 | 1 | 6 | - | 97.69 | 16 |
| 100 | 100.00 | 97.99 | 2 | 4 | 43 | 98.03 | 43 |
| 1000 | 99.93 | 97.70 | 5 | 13 | - | 97.93 | 49 |
Adadelta
RMSPropの改良版になります。$ g $は同じですが、新たに$ s $が出てきます。
$ s $の役割については理解できておりません。
\begin{align}
g_{k+1} &= \gamma g_k + (1 - \gamma)(E^{'}(w_k))^2, g_0 = 0\\
w_{k+1} &= w_k - \frac{\eta \sqrt{s_k}}{\sqrt{g_{k+1}}} E^{'}(w_k)\\
s_{k+1} &= \gamma s_k + (1 - \gamma)(w_{k+1} - w_k)^2, s_0=0
\end{align}
実装
実装は、以下の通り
def Adadelta(W, dW, eta, optimizer_params, optimizer_stats):
if "g" not in optimizer_stats:
optimizer_stats["g"] = np.zeros_like(W)
if "s" not in optimizer_stats:
optimizer_stats["s"] = np.zeros_like(W)
optimizer_stats["g"] = optimizer_params["gamma"] * optimizer_stats["g"] + (1 - optimizer_params["gamma"]) * dW * dW
newW = W - (eta * dW)/np.sqrt(np.maximum(optimizer_stats["g"], 1e-7)) * np.sqrt(np.maximum(optimizer_stats["s"], 1e-7))
optimizer_stats["s"] = (1 - optimizer_params["gamma"]) * (newW - W) * (newW - W) + optimizer_params["gamma"] * optimizer_stats["s"]
return newW, optimizer_stats
実行
$ \gamma $を0.99,0.9~0.5に変更しながら試してみます。
- 学習率 0.1
| $ \gamma $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.99 | 97.33 | 96.68 | 20 | - | - | 96.68 | 50 |
| 0.9 | 97.07 | 96.52 | 23 | - | - | 96.52 | 50 |
| 0.8 | 96.92 | 96.37 | 24 | - | - | 96.39 | 49 |
| 0.7 | 96.80 | 96.34 | 27 | - | - | 96.34 | 50 |
| 0.6 | 96.70 | 96.30 | 28 | - | - | 96.30 | 50 |
| 0.5 | 96.58 | 96.19 | 29 | - | - | 96.20 | 49 |
| SGD | 100.00 | 97.85 | 2 | 5 | - | 97.88 | 34 |
- 学習率 0.01
学習率を小さくすると悪くなりました。
| $ \gamma $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.99 | 90.93 | 91.24 | - | - | - | 91.24 | 50 |
| 0.9 | 90.72 | 91.14 | - | - | - | 91.14 | 50 |
| 0.8 | 90.52 | 91.03 | - | - | - | 91.03 | 50 |
| 0.7 | 90.41 | 90.94 | - | - | - | 90.94 | 50 |
| 0.6 | 90.31 | 90.86 | - | - | - | 90.86 | 50 |
| 0.5 | 90.22 | 90.77 | - | - | - | 90.77 | 50 |
| SGD | 98.08 | 97.08 | 15 | 44 | - | 97.17 | 48 |
- 学習率 1.0
| $ \gamma $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.99 | 100.00 | 97.99 | 1 | 4 | 45 | 98.04 | 48 |
| 0.9 | 99.99 | 97.82 | 3 | 7 | - | 97.95 | 41 |
| 0.8 | 99.94 | 97.78 | 4 | 9 | - | 97.84 | 45 |
| 0.7 | 99.89 | 97.88 | 4 | 9 | - | 97.93 | 29 |
| 0.6 | 99.83 | 97.77 | 4 | 9 | - | 97.86 | 41 |
| 0.5 | 99.74 | 97.68 | 4 | 9 | - | 97.86 | 45 |
| SGD | 98.56 | 95.92 | 4 | - | - | 96.76 | 34 |
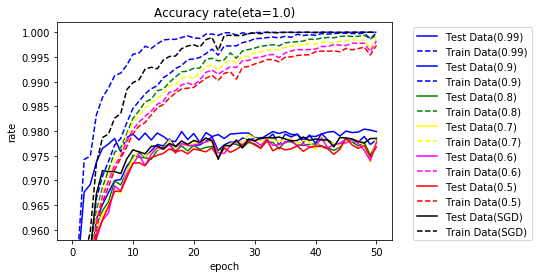
一番良かった、学習率が1.0の場合のグラフです。SGDの学習率は、0.1です。
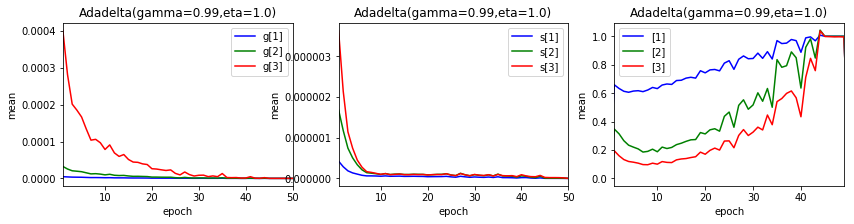
$ g $、$ s $および、学習率に相当する$ \frac{\eta \sqrt{s_k}}{\sqrt{g_{k+1}}} $の値の変化をエポック終了ごとに見てみましょう。値は、各平均値です。
結果の一番良かった、学習率 1.0、$ \gamma $ = 0.99の場合です。
上のグラフは、左から$ g $、$ s $、$ \frac{\eta \sqrt{s_k}}{\sqrt{g_{k+1}}} $です。
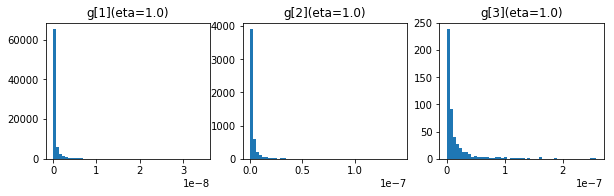
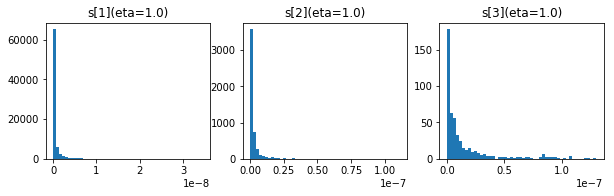
50エポック後の$ g $、$ s $および$ \frac{\eta \sqrt{s_k}}{\sqrt{g_{k+1}}} $の分布です。
上から$ g $、$ s $、$ \frac{\eta}{\sqrt{g}} $です。
平方根がエラーとならないように最小値を1e-7に是正しています。値を変更して試してみます。
| $ \varepsilon $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 1e-4 | 99.16 | 97.21 | 2 | 7 | - | 97.64 | 40 |
| 1e-5 | 99.59 | 97.29 | 1 | 4 | - | 97.87 | 49 |
| 1e-6 | 100.00 | 98.19 | 1 | 4 | 7 | 98.22 | 49 |
| 1e-7 | 100.00 | 97.99 | 1 | 4 | 45 | 98.04 | 48 |
| 1e-8 | 99.95 | 97.85 | 2 | 7 | - | 97.90 | 36 |
| 1e-9 | 98.72 | 97.39 | 4 | 20 | - | 97.50 | 47 |
グラフ化します。やはり、$ g $、$ s $の値がほとんど0のため影響が大きいです。
バッチサイズを変更してみます。学習率は、1.0、$ \gamma $は、0.99です。
| バッチサイズ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 10 | 100.00 | 98.18 | 1 | 2 | 14 | 98.19 | 33 |
| 100 | 100.00 | 97.99 | 1 | 4 | 45 | 98.04 | 48 |
| 1000 | 99.82 | 97.78 | 5 | 14 | - | 97.97 | 45 |
Adam
$ v $は、Adadeltaの$ g $と同じです。
あとの説明はできません。悪しからず。
\begin{align}
m_{k+1} &= \beta_1 m_k + (1 - \beta_1)E^{'}(w_k),m_0 = 0\\
v_{k+1} &= \beta_2 v_k + (1 - \beta_2)(E^{'}(w_k))^2,v_0 = 0\\
\hat{m}_k &= \frac{m_k}{1 - \beta_1^k}\\
\hat{v}_k &= \frac{v_k}{1 - \beta_2^k}\\
w_{k+1} &= w_k - \frac{\eta \hat{m}_{k+1}}{\sqrt{\hat{v}_{k+1}}}
\end{align}
実装
実装は、以下です。
def Adam(W, dW, eta, optimizer_params, optimizer_stats):
if "k" not in optimizer_stats:
optimizer_stats["k"] = 0
if "m" not in optimizer_stats:
optimizer_stats["m"] = np.zeros_like(W)
if "v" not in optimizer_stats:
optimizer_stats["v"] = np.zeros_like(W)
optimizer_stats["k"] = optimizer_stats["k"] + 1
optimizer_stats["m"] = optimizer_params["beta1"] * optimizer_stats["m"] + (1 - optimizer_params["beta1"]) * dW
optimizer_stats["v"] = optimizer_params["beta2"] * optimizer_stats["v"] + (1 - optimizer_params["beta2"]) * dW * dW
hatm = optimizer_stats["m"] / (1 - np.power(optimizer_params["beta1"], optimizer_stats["k"]))
hatv = optimizer_stats["v"] / (1 - np.power(optimizer_params["beta2"], optimizer_stats["k"]))
return W - eta / np.maximum(np.sqrt(hatv), 1e-7) * hatm, optimizer_stats
実行
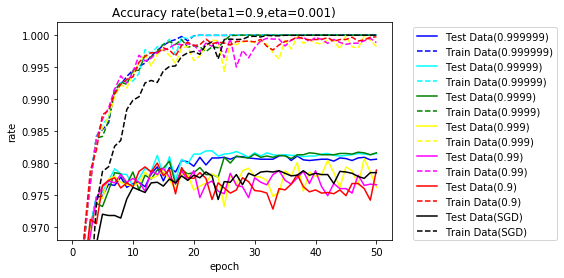
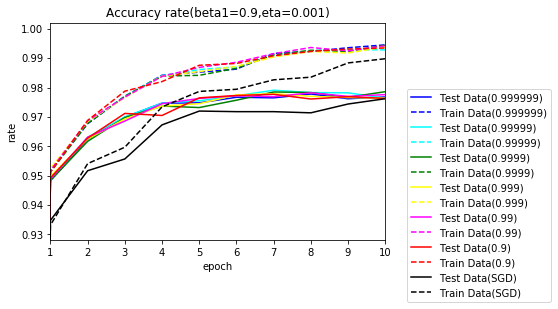
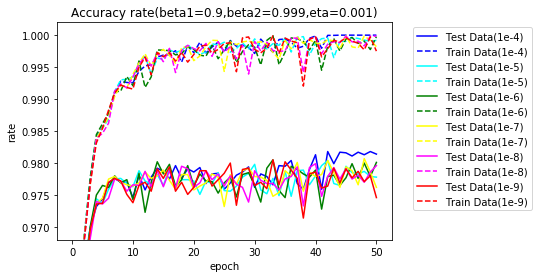
まず、学習率を変更し試してみます。$ \beta_1 $、$ \beta_2 $は、良いとされる0.9、0.999です。
| 学習率 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 1.0 | 10.44 | 10.28 | - | - | - | 11.35 | 3 |
| 0.1 | 20.74 | 20.98 | - | - | - | 72.47 | 3 |
| 0.01 | 99.30 | 97.19 | 1 | 9 | - | 97.49 | 44 |
| 0.001 | 99.82 | 97.62 | 2 | 4 | 37 | 98.07 | 48 |
| 0.0001 | 99.53 | 97.69 | 7 | 21 | - | 97.69 | 50 |
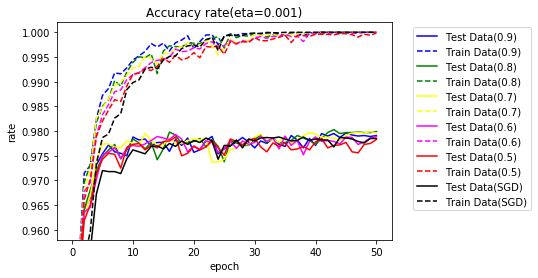
学習率は、0.001が良さそうです。$ \beta_1 $、$ \beta_2 $を変更し実行します。
$ \beta_1 $は、0.99、0.9~0.5、$ \beta_2 $は、0.999999、0.99999、0.9999、0.999、0.99、0.9とします。
- $ \beta_2 $ = 0.999999
| $ \beta_1 $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.99 | 100.00 | 98.08 | 2 | 5 | 19 | 98.14 | 25 |
| 0.9 | 100.00 | 98.06 | 2 | 4 | 18 | 98.13 | 35 |
| 0.8 | 100.00 | 98.02 | 2 | 4 | 31 | 98.09 | 42 |
| 0.7 | 100.00 | 98.05 | 2 | 4 | 22 | 98.10 | 22 |
| 0.6 | 100.00 | 97.93 | 2 | 4 | - | 97.98 | 35 |
| 0.5 | 100.00 | 98.07 | 2 | 4 | 19 | 98.08 | 49 |
- $ \beta_2 $ = 0.99999
| $ \beta_1 $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.99 | 100.00 | 98.02 | 2 | 5 | 16 | 98.08 | 25 |
| 0.9 | 100.00 | 98.15 | 2 | 3 | 14 | 98.19 | 22 |
| 0.8 | 100.00 | 98.04 | 2 | 4 | 24 | 98.09 | 48 |
| 0.7 | 100.00 | 97.93 | 2 | 4 | - | 97.94 | 19 |
| 0.6 | 100.00 | 97.99 | 2 | 4 | 22 | 98.04 | 22 |
| 0.5 | 100.00 | 98.06 | 2 | 4 | 20 | 98.08 | 27 |
- $ \beta_2 $ = 0.9999
| $ \beta_1 $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.99 | 100.00 | 98.00 | 2 | 5 | 27 | 98.05 | 27 |
| 0.9 | 100.00 | 98.16 | 2 | 4 | 16 | 98.17 | 47 |
| 0.8 | 100.00 | 98.06 | 2 | 4 | 33 | 98.08 | 45 |
| 0.7 | 100.00 | 97.94 | 2 | 4 | - | 97.97 | 28 |
| 0.6 | 100.00 | 97.96 | 2 | 4 | 22 | 98.02 | 37 |
| 0.5 | 100.00 | 98.03 | 2 | 4 | 38 | 98.03 | 50 |
- $ \beta_2 $ = 0.999
| $ \beta_1 $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.99 | 99.88 | 97.64 | 2 | 5 | - | 97.97 | 44 |
| 0.9 | 99.82 | 97.62 | 2 | 4 | 37 | 98.07 | 48 |
| 0.8 | 99.85 | 97.77 | 1 | 4 | 30 | 98.12 | 30 |
| 0.7 | 100.00 | 98.15 | 2 | 4 | 49 | 98.15 | 50 |
| 0.6 | 100.00 | 97.96 | 2 | 4 | - | 97.97 | 49 |
| 0.5 | 100.00 | 97.96 | 2 | 4 | 37 | 98.06 | 37 |
- $ \beta_2 $ = 0.99
| $ \beta_1 $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.99 | 99.92 | 97.72 | 2 | 4 | - | 97.98 | 15 |
| 0.9 | 99.88 | 97.66 | 2 | 4 | - | 97.92 | 15 |
| 0.8 | 99.88 | 97.55 | 2 | 4 | 45 | 98.00 | 45 |
| 0.7 | 99.71 | 97.58 | 2 | 4 | 49 | 98.02 | 49 |
| 0.6 | 99.93 | 97.68 | 2 | 4 | - | 97.92 | 26 |
| 0.5 | 99.95 | 97.73 | 2 | 4 | 36 | 98.06 | 36 |
- $ \beta_2 $ = 0.9
| $ \beta_1 $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.99 | 97.83 | 95.89 | 8 | - | - | 96.34 | 42 |
| 0.9 | 99.97 | 97.89 | 2 | 3 | 14 | 98.00 | 14 |
| 0.8 | 99.95 | 97.57 | 2 | 4 | - | 97.94 | 16 |
| 0.7 | 99.96 | 97.80 | 2 | 4 | - | 97.97 | 42 |
| 0.6 | 99.96 | 97.74 | 2 | 4 | - | 97.98 | 43 |
| 0.5 | 99.99 | 97.80 | 2 | 4 | - | 97.91 | 29 |
$ \beta_1 $は、0.9が、$ \beta_2 $は、1に近いほど良さそうです。
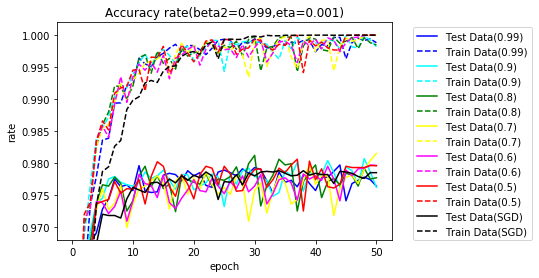
$ \beta_2 $=0.999とし、$ \beta_1 $を変更した際のグラフです。参考のためSGDも含めます。SGDの学習率は、0.1です。
10エポックまで拡大します。
序盤は、Adamの方が早く学習が進んでいます。
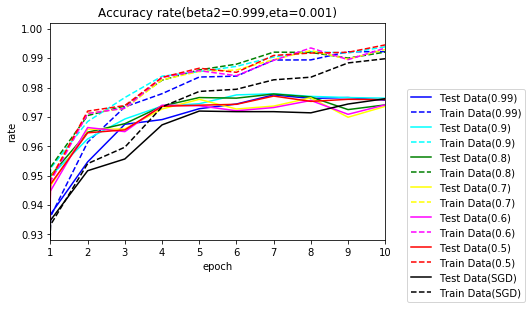
今度は、$ \beta_1 $=0.9とし、$ \beta_2 $を変更した際のグラフです。
10エポックまで拡大します。
こちらも序盤は、Adamの方が早く学習が進んでいます。
平方根がエラーとならないようにするための是正値、1e-7を変更して試してみます。
| $ \varepsilon $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 1e-4 | 100.00 | 98.14 | 2 | 4 | 36 | 98.18 | 42 |
| 1e-5 | 99.92 | 97.78 | 2 | 3 | 42 | 98.04 | 42 |
| 1e-6 | 99.98 | 98.01 | 2 | 3 | 14 | 98.05 | 33 |
| 1e-7 | 99.82 | 97.62 | 2 | 4 | 37 | 98.07 | 48 |
| 1e-8 | 99.99 | 97.96 | 2 | 4 | - | 97.99 | 40 |
| 1e-9 | 99.75 | 97.46 | 2 | 4 | 26 | 98.05 | 33 |
グラフ化します。
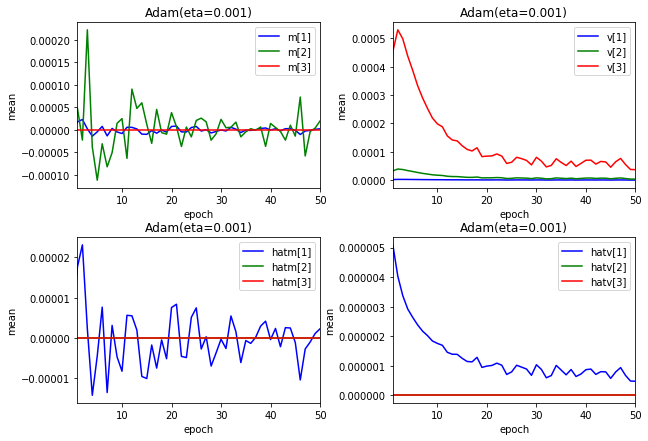
$ m $、$ v $のエポックごとの変化を見てみます。$ \hat{m} $、$ \hat{v} $も表示します。
$ m $、$ v $の50エポック後の分布です。
最後にバッチサイズの変更です。
| バッチサイズ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 10 | 99.70 | 97.54 | 1 | 2 | 13 | 98.05 | 13 |
| 100 | 99.82 | 97.62 | 2 | 4 | 37 | 98.07 | 48 |
| 1000 | 99.98 | 97.68 | 5 | 12 | - | 97.76 | 30 |
実装変更
平方根の0防止のための$ \varepsilon $をパラメータとして指定できるようにします。既定値は、1e-7です。
def AdaGrad(W, dW, eta, optimizer_params, optimizer_stats):
epsilon = 1e-7
if "epsilon" in optimizer_params:
epsilon = optimizer_params["epsilon"]
if "g" not in optimizer_stats:
optimizer_stats["g"] = np.zeros_like(W)
optimizer_stats["g"] = optimizer_stats["g"] + (dW * dW)
return W - (eta * dW)/np.sqrt(np.maximum(optimizer_stats["g"], epsilon)), optimizer_stats
def RMSProp(W, dW, eta, optimizer_params, optimizer_stats):
epsilon = 1e-7
if "epsilon" in optimizer_params:
epsilon = optimizer_params["epsilon"]
if "g" not in optimizer_stats:
optimizer_stats["g"] = np.zeros_like(W)
optimizer_stats["g"] = optimizer_params["gamma"] * optimizer_stats["g"] + (1 - optimizer_params["gamma"]) * dW * dW
return W - (eta * dW)/np.sqrt(np.maximum(optimizer_stats["g"], epsilon)), optimizer_stats
def Adadelta(W, dW, eta, optimizer_params, optimizer_stats):
epsilon = 1e-7
if "epsilon" in optimizer_params:
epsilon = optimizer_params["epsilon"]
if "g" not in optimizer_stats:
optimizer_stats["g"] = np.zeros_like(W)
if "s" not in optimizer_stats:
optimizer_stats["s"] = np.zeros_like(W)
optimizer_stats["g"] = optimizer_params["gamma"] * optimizer_stats["g"] + (1 - optimizer_params["gamma"]) * dW * dW
newW = W - (eta * dW)/np.sqrt(np.maximum(optimizer_stats["g"], epsilon)) * np.sqrt(np.maximum(optimizer_stats["s"], epsilon))
optimizer_stats["s"] = (1 - optimizer_params["gamma"]) * (newW - W) * (newW - W) + optimizer_params["gamma"] * optimizer_stats["s"]
return newW, optimizer_stats
def Adam(W, dW, eta, optimizer_params, optimizer_stats):
epsilon = 1e-7
if "epsilon" in optimizer_params:
epsilon = optimizer_params["epsilon"]
if "k" not in optimizer_stats:
optimizer_stats["k"] = 0
if "m" not in optimizer_stats:
optimizer_stats["m"] = np.zeros_like(W)
if "v" not in optimizer_stats:
optimizer_stats["v"] = np.zeros_like(W)
optimizer_stats["k"] = optimizer_stats["k"] + 1
optimizer_stats["m"] = optimizer_params["beta1"] * optimizer_stats["m"] + (1 - optimizer_params["beta1"]) * dW
optimizer_stats["v"] = optimizer_params["beta2"] * optimizer_stats["v"] + (1 - optimizer_params["beta2"]) * dW * dW
hatm = optimizer_stats["m"] / (1 - np.power(optimizer_params["beta1"], optimizer_stats["k"]))
hatv = optimizer_stats["v"] / (1 - np.power(optimizer_params["beta2"], optimizer_stats["k"]))
return W - eta / np.maximum(np.sqrt(hatv), epsilon) * hatm, optimizer_stats
結果の整理
各手法の式を再掲します。
- Momentum
\begin{align}
v_{k+1} &= \mu v_k - \eta E^{'}(w_k), v_0 = 0\\
w_{k+1} &= w_k + v_{k+1}
\end{align}
- Nestrovの加速勾配法
\begin{align}
v_{k+1} &= \mu v_k - \eta E^{'}(w_k + \mu v_k), v_0 = 0\\
w_{k+1} &= w_k + v_{k+1}
\end{align}
- AdaGrad
\begin{align}
g_{k+1} &= g_k + (E^{'}(w_k))^2, g_0 = 0\\
w_{k+1} &= w_k - \frac{\eta}{\sqrt{g_{k+1}}} E^{'}(w_k)
\end{align}
- RMSProp
\begin{align}
g_{k+1} &= \gamma g_k + (1 - \gamma)(E^{'}(w_k))^2, g_0 = 0\\
w_{k+1} &= w_k - \frac{\eta}{\sqrt{g_{k+1}}} E^{'}(w_k)
\end{align}
- Adadelta
\begin{align}
g_{k+1} &= \gamma g_k + (1 - \gamma)(E^{'}(w_k))^2, g_0 = 0\\
w_{k+1} &= w_k - \frac{\eta \sqrt{s_k}}{\sqrt{g_{k+1}}} E^{'}(w_k)\\
s_{k+1} &= \gamma s_k + (1 - \gamma)(w_{k+1} - w_k)^2, s_0=0
\end{align}
- Adam
\begin{align}
m_{k+1} &= \beta_1 m_k + (1 - \beta_1)E^{'}(w_k),m_0 = 0\\
v_{k+1} &= \beta_2 v_k + (1 - \beta_2)(E^{'}(w_k))^2,v_0 = 0\\
\hat{m}_k &= \frac{m_k}{1 - \beta_1^k}\\
\hat{v}_k &= \frac{v_k}{1 - \beta_2^k}\\
w_{k+1} &= w_k - \frac{\eta \hat{m}_{k+1}}{\sqrt{\hat{v}_{k+1}}}
\end{align}
各手法の結果比較
以下のパラメータで実行し比較します。
| 手法 | 学習率 | パラメータ |
|---|---|---|
| SGD | 0.1 | |
| Momentum | 0.1 | $ \mu = 0.8 $ |
| Nesterov | 0.1 | $ \mu = 0.8 $ |
| AdaGrad | 0.01 | |
| RMSProp | 0.001 | $ \gamma = 0.8 $ |
| Adadelta | 1.0 | $ \gamma = 0.99 $ |
| Adam | 0.001 | $ \beta1 = 0.9 $、$ \beta2 = 0.999 $ |
実行プログラム
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
Ws = {}
bs = {}
train_rates = {}
train_errs = {}
test_rates = {}
test_errs = {}
total_times = {}
# SGD
name="SGD"
_, _, Ws[name], bs[name], train_rates[name], train_errs[name], test_rates[name], test_errs[name], total_times[name] = learn(
name, x_train, t_train, x_test, t_test
)
# Momentum
name="Momentum"
_, _, Ws[name], bs[name], train_rates[name], train_errs[name], test_rates[name], test_errs[name], total_times[name] = learn(
name, x_train, t_train, x_test, t_test,
optimizer_func = Momentum, optimizer_params = {"mu":0.8}
)
# Nesterov
name="Nesterov"
_, _, Ws[name], bs[name], train_rates[name], train_errs[name], test_rates[name], test_errs[name], total_times[name] = learn(
name, x_train, t_train, x_test, t_test,
optimizer_func = Nesterov, optimizer_params = {"mu":0.8}
)
# AdaGrad
name="AdaGrad"
_, _, Ws[name], bs[name], train_rates[name], train_errs[name], test_rates[name], test_errs[name], total_times[name] = learn(
name, x_train, t_train, x_test, t_test, eta=0.01,
optimizer_func = AdaGrad
)
# RMSProp
name="RMSProp"
_, _, Ws[name], bs[name], train_rates[name], train_errs[name], test_rates[name], test_errs[name], total_times[name] = learn(
name, x_train, t_train, x_test, t_test, eta=0.001,
optimizer_func = RMSProp, optimizer_params = {"gamma":0.8}
)
# Adadelta
name="Adadelta"
_, _, Ws[name], bs[name], train_rates[name], train_errs[name], test_rates[name], test_errs[name], total_times[name] = learn(
name, x_train, t_train, x_test, t_test, eta=1.0,
optimizer_func = Adadelta, optimizer_params = {"gamma":0.99}
)
# Adam
name="Adam"
_, _, Ws[name], bs[name], train_rates[name], train_errs[name], test_rates[name], test_errs[name], total_times[name] = learn(
name, x_train, t_train, x_test, t_test, eta=0.001,
optimizer_func = Adam, optimizer_params = {"beta1":0.9,"beta2":0.999}
)
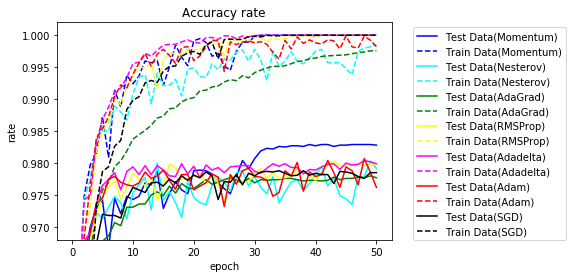
結果の正解率のグラフです。
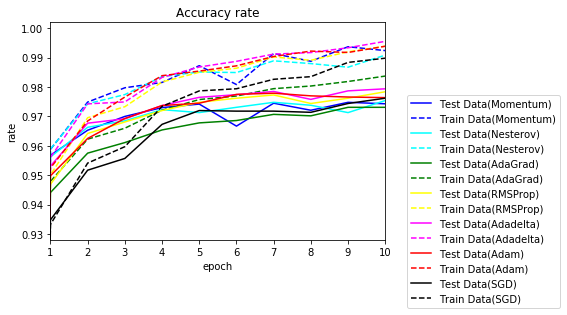
10エポックまで拡大します。
いずれもSGDより早く学習が進んでいます。
どの手法がよいか、試してみないと分かりません。特に、学習率が各手法のパラメータ、バッチサイズだけでなく、$ \varepsilon $にも影響されハイパーパラメータの値の決定が大変なことが分かりました。
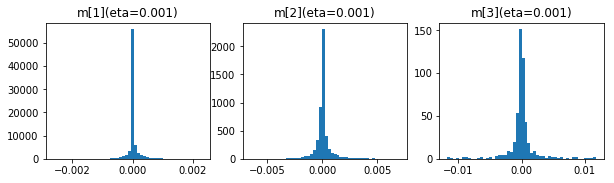
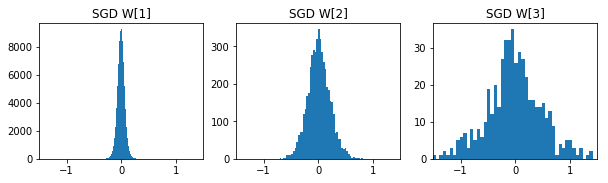
参考までに各手法の50エポック後の重みの分布です。
- SGD
- Momentum
- Nesterov
- AdaGrad
- RMSProp
- Adadelta
- Adam
バッチ正規化への適用
バッチ正規化も$ \gamma $、$ \beta $を学習します。バッチ正規化に適用するとどうなるかも試してみます。
実装
初期化処理
optimizer_stats_gamma = {}
optimizer_stats_beta = {}
for i in range(1, layer):
optimizer_stats_gamma[i] = {}
optimizer_stats_beta[i] = {}
$ \gamma $、$ \beta $の調整
# バッチ正規化の調整
if regularization_params.get("batch_norm"):
for k in range(1, layer):
batch_norm_params["batch_norm_gamma"][k], optimizer_stats_gamma[k] = optimizer_func(batch_norm_params["batch_norm_gamma"][k], batch_norm_dparams["batch_norm_dgamma"][k], batch_norm_eta, optimizer_params, optimizer_stats_gamma[k])
batch_norm_params["batch_norm_beta"][k], optimizer_stats_beta[k] = optimizer_func(batch_norm_params["batch_norm_beta"][k], batch_norm_dparams["batch_norm_dbeta"][k], batch_norm_eta, optimizer_params, optimizer_stats_beta[k])
実行
バッチ正規化適用有無および$ \gamma $、$ \beta $の調整に勾配法を適用するかどうかで違いを確認します。
パラメータは、各手法の結果比較と同じです。
- Momentum
| バッチ正規化 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 無 | 100.00 | 98.28 | 1 | 3 | 28 | 98.29 | 39 |
| 有 | 100.00 | 98.14 | 1 | 2 | 7 | 98.37 | 43 |
| 有($ \gamma $、$ \beta $適用) | 100.00 | 98.12 | 1 | 2 | 11 | 98.34 | 47 |
- Nesterov
| バッチ正規化 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 無 | 99.86 | 97.92 | 1 | 4 | 14 | 98.03 | 49 |
| 有 | 100.00 | 98.21 | 1 | 2 | 6 | 98.30 | 32 |
| 有($ \gamma $、$ \beta $適用) | 100.00 | 98.03 | 1 | 2 | 6 | 98.21 | 14 |
- AdaGrad
| バッチ正規化 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 無 | 99.76 | 97.77 | 2 | 7 | - | 97.80 | 49 |
| 有 | 100.00 | 98.10 | 1 | 3 | 27 | 98.14 | 44 |
| 有($ \gamma $、$ \beta $適用) | 100.00 | 98.01 | 1 | 2 | 23 | 98.06 | 49 |
- RMSProp
| バッチ正規化 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 無 | 100.00 | 97.99 | 2 | 4 | 43 | 98.03 | 43 |
| 有 | 99.99 | 97.99 | 1 | 2 | 30 | 98.16 | 41 |
| 有($ \gamma $、$ \beta $適用) | 99.99 | 98.03 | 1 | 2 | 15 | 98.14 | 33 |
- Adadelta
| バッチ正規化 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 無 | 100.00 | 97.99 | 1 | 4 | 45 | 98.04 | 48 |
| 有 | 99.97 | 97.72 | 1 | 2 | 29 | 98.06 | 29 |
| 有($ \gamma $、$ \beta $適用) | 99.99 | 97.95 | 1 | 2 | 7 | 98.10 | 9 |
- Adam
| バッチ正規化 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 無 | 99.82 | 97.62 | 2 | 4 | 37 | 98.07 | 48 |
| 有 | 99.97 | 98.17 | 1 | 2 | 12 | 98.20 | 49 |
| 有($ \gamma $、$ \beta $適用) | 99.97 | 97.95 | 1 | 2 | 7 | 98.37 | 36 |
バッチ正規化の$ \gamma $、$ \beta $の更新に勾配法を適用する方がよいかどうかは微妙です。適用すると良くなるケースと悪くなるケースがあります。
ただし、適用すると学習が早く進む傾向があるので適用することにします。
参考
今回のプログラムです。
import gzip
import numpy as np
# MNIST読み込み
def load_mnist( mnist_path ) :
return _load_image(mnist_path + 'train-images-idx3-ubyte.gz'), \
_load_label(mnist_path + 'train-labels-idx1-ubyte.gz'), \
_load_image(mnist_path + 't10k-images-idx3-ubyte.gz'), \
_load_label(mnist_path + 't10k-labels-idx1-ubyte.gz')
def _load_image( image_path ) :
# 画像データの読み込み
with gzip.open(image_path, 'rb') as f:
buffer = f.read()
size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
rows = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=8)
columns = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=12)
data = np.frombuffer(buffer, np.uint8, offset=16)
image = np.reshape(data, (size[0], rows[0]*columns[0]))
image = image.astype(np.float32)
return image
def _load_label( label_path ) :
# 正解データ読み込み
with gzip.open(label_path, 'rb') as f:
buffer = f.read()
size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
data = np.frombuffer(buffer, np.uint8, offset=8)
label = np.zeros((size[0], 10))
for i in range(size[0]):
label[i, data[i]] = 1
return label
# 正規化関数
def min_max(x, stats, params):
axis=params.get("axis")
if "min" not in stats:
stats["min"] = np.min(x, axis=axis, keepdims=True) # 最小値を求める
if "max" not in stats:
stats["max"] = np.max(x, axis=axis, keepdims=True) # 最大値を求める
return (x-stats["min"])/np.maximum((stats["max"]-stats["min"]),1e-7), stats
def z_score(x, stats, params):
axis=params.get("axis")
if "mean" not in stats:
stats["mean"] = np.mean(x, axis=axis, keepdims=True) # 平均値を求める
if "std" not in stats:
stats["std"] = np.std(x, axis=axis, keepdims=True) # 標準偏差を求める
return (x-stats["mean"])/np.maximum(stats["std"],1e-7), stats
# affine変換
def affine(z, W, b):
return np.dot(z, W) + b
def affine_back(du, z, W, b):
dz = np.dot(du, W.T) # zの勾配は、今までの勾配と重みを掛けた値
dW = np.dot(z.T, du) # 重みの勾配は、zに今までの勾配を掛けた値
size = 1
if z.ndim == 2:
size = z.shape[0]
db = np.dot(np.ones(size).T, du) # バイアスの勾配は、今までの勾配の値
return dz, dW, db
# 活性化関数(中間)
def sigmoid(u, params):
return 1/(1 + np.exp(-u))
def sigmoid_back(dz, u, z, params):
return dz * (z - z**2)
def tanh(u, params):
return np.tanh(u)
def tanh_back(dz, u, z, params):
return dz * (1/np.cosh(u)**2)
def relu(u, params):
return np.maximum(0, u)
def relu_back(dz, u, z, params):
return dz * np.where(u > 0, 1, 0)
def leaky_relu(u, params):
return np.maximum(u * params["alpha"], u)
def leaky_relu_back(dz, u, z, params):
return dz * np.where(u > 0, 1, params["alpha"])
def identity(u, params):
return u
def identity_back(dz, u, z, params):
return dz
def softplus(u, params):
return np.log(1+np.exp(u))
def softplus_back(dz, u, z, params):
return dz * (1/(1 + np.exp(-u)))
def softsign(u, params):
return u/(1+np.absolute(u))
def softsign_back(dz, u, z, params):
return dz * (1/(1+np.absolute(u))**2)
def step(u, params):
return np.where(u > 0, 1, 0)
def step_back(dz, u, x, params):
return 0
# 活性化関数(出力)
def softmax(u, params):
u = u.T
max_u = np.max(u, axis=0)
exp_u = np.exp(u - max_u)
sum_exp_u = np.sum(exp_u, axis=0)
y = exp_u/sum_exp_u
return y.T
# 損失関数
def mean_squared_error(y, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return 0.5 * np.sum((y-t)**2)/size
def cross_entropy_error(y, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return -np.sum(t * np.log(np.maximum(y,1e-7)))/size
#return -np.sum(t * np.log(y))/size
# 活性化関数(出力)+損失関数勾配
def softmax_cross_entropy_error_back(y, u, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return (y - t)/size
def identity_mean_squared_error_back(y, u, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return (y - t)/size
# 重み・バイアスの初期化
def lecun_normal(d_1, d, params):
var = 1/np.sqrt(d_1)
return np.random.normal(0, var, (d_1, d))
def lecun_uniform(d_1, d, params):
min = -np.sqrt(3/d_1)
max = np.sqrt(3/d_1)
return np.random.uniform(min, max, (d_1, d))
def glorot_normal(d_1, d, params):
var = np.sqrt(2/(d_1+d))
return np.random.normal(0, var, (d_1, d))
def glorot_uniform(d_1, d, params):
min = -np.sqrt(6/(d_1+d))
max = np.sqrt(6/(d_1+d))
return np.random.uniform(min, max, (d_1, d))
def he_normal(d_1, d, params):
var = np.sqrt(2/d_1)
return np.random.normal(0, var, (d_1, d))
def he_uniform(d_1, d, params):
min = -np.sqrt(6/d_1)
max = np.sqrt(6/d_1)
return np.random.uniform(min, max, (d_1, d))
def normal_w(d_1, d, params):
mean=0
var=1
if "mean" in params:
mean = params["mean"]
if "var" in params:
var = params["var"]
return np.random.normal(mean, var, (d_1, d))
def normal_b(d, params):
mean=0
var=1
if "mean" in params:
mean = params["mean"]
if "var" in params:
var = params["var"]
return np.random.normal(mean, var, d)
def uniform_w(d_1, d, params):
min=0
max=1
if "min" in params:
min = params["min"]
if "max" in params:
max = params["max"]
return np.random.uniform(min, max, (d_1, d))
def uniform_b(d, params):
min=0
max=1
if "min" in params:
min = params["min"]
if "max" in params:
max = params["max"]
return np.random.uniform(min, max, d)
def zeros_w(d_1, d, params):
return np.zeros((d_1, d))
def zeros_b(d, params):
return np.zeros(d)
def ones_w(d_1, d, params):
return np.ones((d_1, d))
def ones_b(d, params):
return np.ones(d)
# 勾配法
def SGD(W, dW, eta, optimizer_params, optimizer_stats):
return W - eta*dW, optimizer_stats
def Momentum(W, dW, eta, optimizer_params, optimizer_stats):
if "v" not in optimizer_stats: # vの初期値設定
optimizer_stats["v"] = np.zeros_like(W)
# vの更新
optimizer_stats["v"] = optimizer_params["mu"] * optimizer_stats["v"] - eta * dW
return W + optimizer_stats["v"], optimizer_stats
def Nesterov(W, dW, eta, optimizer_params, optimizer_stats):
if "v" not in optimizer_stats:
optimizer_stats["v"] = np.zeros_like(W)
optimizer_stats["v"] = optimizer_params["mu"] * optimizer_stats["v"] - eta * dW
return W + optimizer_stats["v"], optimizer_stats
def AdaGrad(W, dW, eta, optimizer_params, optimizer_stats):
epsilon = 1e-7
if "epsilon" in optimizer_params:
epsilon = optimizer_params["epsilon"]
if "g" not in optimizer_stats:
optimizer_stats["g"] = np.zeros_like(W)
optimizer_stats["g"] = optimizer_stats["g"] + (dW * dW)
return W - (eta * dW)/np.sqrt(np.maximum(optimizer_stats["g"], epsilon)), optimizer_stats
def RMSProp(W, dW, eta, optimizer_params, optimizer_stats):
epsilon = 1e-7
if "epsilon" in optimizer_params:
epsilon = optimizer_params["epsilon"]
if "g" not in optimizer_stats:
optimizer_stats["g"] = np.zeros_like(W)
optimizer_stats["g"] = optimizer_params["gamma"] * optimizer_stats["g"] + (1 - optimizer_params["gamma"]) * dW * dW
return W - (eta * dW)/np.sqrt(np.maximum(optimizer_stats["g"], epsilon)), optimizer_stats
def Adadelta(W, dW, eta, optimizer_params, optimizer_stats):
epsilon = 1e-7
if "epsilon" in optimizer_params:
epsilon = optimizer_params["epsilon"]
if "g" not in optimizer_stats:
optimizer_stats["g"] = np.zeros_like(W)
if "s" not in optimizer_stats:
optimizer_stats["s"] = np.zeros_like(W)
optimizer_stats["g"] = optimizer_params["gamma"] * optimizer_stats["g"] + (1 - optimizer_params["gamma"]) * dW * dW
newW = W - (eta * dW)/np.sqrt(np.maximum(optimizer_stats["g"], epsilon)) * np.sqrt(np.maximum(optimizer_stats["s"], epsilon))
optimizer_stats["s"] = (1 - optimizer_params["gamma"]) * (newW - W) * (newW - W) + optimizer_params["gamma"] * optimizer_stats["s"]
return newW, optimizer_stats
def Adam(W, dW, eta, optimizer_params, optimizer_stats):
epsilon = 1e-7
if "epsilon" in optimizer_params:
epsilon = optimizer_params["epsilon"]
if "k" not in optimizer_stats:
optimizer_stats["k"] = 0
if "m" not in optimizer_stats:
optimizer_stats["m"] = np.zeros_like(W)
if "v" not in optimizer_stats:
optimizer_stats["v"] = np.zeros_like(W)
optimizer_stats["k"] = optimizer_stats["k"] + 1
optimizer_stats["m"] = optimizer_params["beta1"] * optimizer_stats["m"] + (1 - optimizer_params["beta1"]) * dW
optimizer_stats["v"] = optimizer_params["beta2"] * optimizer_stats["v"] + (1 - optimizer_params["beta2"]) * dW * dW
hatm = optimizer_stats["m"] / (1 - np.power(optimizer_params["beta1"], optimizer_stats["k"]))
hatv = optimizer_stats["v"] / (1 - np.power(optimizer_params["beta2"], optimizer_stats["k"]))
return W - eta / np.maximum(np.sqrt(hatv), epsilon) * hatm, optimizer_stats
# 重み減衰
def L1_norm(W, weight_decay_lambda):
r = 0.
for WI in W.values():
r = r + np.sum(np.absolute(WI))
return weight_decay_lambda * r
def L1_norm_back(W, weight_decay_lambda):
return np.where(W > 0, weight_decay_lambda, np.where(W < 0, -weight_decay_lambda, 0))
def L2_norm(W, weight_decay_lambda):
r = 0.
for WI in W.values():
r = r + np.sum(WI**2)
return (weight_decay_lambda * r)/2
def L2_norm_back(W, weight_decay_lambda):
return weight_decay_lambda * W
# ドロップアウト
def dropout(z, mask):
return z * mask
def dropout_back(dz, mask):
return dz * mask
# バッチ正規化
def batch_norm(x, gamma, beta, axis = 0):
x_mean = np.mean(x, axis=axis, keepdims=True) # 平均値を求める
x_std = np.maximum(np.std(x, axis=axis, keepdims=True),1e-7) # 標準偏差を求める
xh = (x-x_mean)/x_std # 正規化
return gamma * xh + beta
def batch_norm_back(dy, x, gamma, beta, axis = 0):
m = x.shape[axis] # バッチサイズ
x_mean = np.mean(x, axis=axis, keepdims=True) # 平均値を求める
x_std = np.maximum(np.std(x, axis=axis, keepdims=True),1e-7) # 標準偏差を求める
xh = (x-x_mean)/x_std # 正規化
gdy = dy * gamma
dy_sum = np.sum(gdy * (x - x_mean), axis=axis, keepdims=True)
dz = (gdy - (xh * dy_sum /(m * x_std)))/ x_std
dz_sum = np.sum(dz, axis=axis, keepdims=True)
dx = dz - (dz_sum / m)
dgamma = np.sum(xh * dy, axis=axis, keepdims=True)
dbeta = np.sum(dy, axis=axis, keepdims=True)
return dx, dgamma, dbeta
# 正解率
def accuracy_rate(y, t):
max_y = np.argmax(y, axis=1)
max_t = np.argmax(t, axis=1)
return np.sum(max_y == max_t)/y.shape[0]
import numpy as np
# ドロップアウト
def set_dropout_mask(d, regularization_params):
mask = {}
if "dropout_input_ratio" in regularization_params:
mask[0] = np.zeros(d[0])
ratio = regularization_params["dropout_input_ratio"]
mask_idx = np.random.choice(d[0], round(ratio*d[0]), replace=False) # 通すindexの配列
mask[0][mask_idx] = 1
if "dropout_middle_ratio" in regularization_params:
for i in range(1, len(d)-1):
mask[i] = np.zeros(d[i])
ratio = regularization_params["dropout_middle_ratio"]
mask_idx = np.random.choice(d[i], round(ratio*d[i]), replace=False) # 通すindexの配列
mask[i][mask_idx] = 1
return mask
# affin計算
def calc_affine(z, W, b):
return affine(z, W, b)
# affin勾配計算
def calc_affine_back(du, z, W, b, regularization_params):
dz, dW, db = affine_back(du, z, W, b)
if "weight_decay_func" in regularization_params: # 重み減衰対応
dW = dW + regularization_params["weight_decay_back_func"](W, regularization_params["weight_decay_lambda"])
return dz, dW, db
# 入力計算
def calc_input(x, regularization_params, dropout_mask):
# ドロップアウト対応
if "dropout_input_ratio" in regularization_params:
if dropout_mask is not None:
x = dropout(x, dropout_mask)
else:
x = x * regularization_params["dropout_input_ratio"]
return x
# 活性化関数計算
def calc_middle(u, middle_func, middle_params, regularization_params, batch_norm_gamma, batch_norm_beta, dropout_mask):
# バッチ正規化対応
un = u
if regularization_params.get("batch_norm"):
un = batch_norm(u, batch_norm_gamma, batch_norm_beta)
# 活性化関数
z = middle_func(un, middle_params)
# ドロップアウト対応
if "dropout_middle_ratio" in regularization_params:
if dropout_mask is not None:
z = dropout(z, dropout_mask)
else:
z = z * regularization_params["dropout_middle_ratio"]
return un, z
# 活性化関数勾配計算
def calc_middle_back(dz, u, un, z, middle_back_func, middle_params, regularization_params, batch_norm_gamma, batch_norm_beta, dropout_mask):
# ドロップアウト対応
if dropout_mask is not None:
dz = dropout_back(dz, dropout_mask)
# 活性化関数勾配
du = middle_back_func(dz, un, z, middle_params)
# バッチ正規化対応
batch_norm_dgamma = None
batch_norm_dbeta = None
if regularization_params.get("batch_norm"):
du, batch_norm_dgamma, batch_norm_dbeta = batch_norm_back(du, u, batch_norm_gamma, batch_norm_beta)
return du, batch_norm_dgamma, batch_norm_dbeta
# 誤差計算
def calc_error(y, t, W, error_func, regularization_params):
e = error_func(y, t)
if "weight_decay_func" in regularization_params: # 重み減衰対応
e = e + regularization_params["weight_decay_func"](W, regularization_params["weight_decay_lambda"])
return e
# 順伝播
def propagation(layer, x, W, b, middle_func, middle_params, output_func, output_params, regularization_params, batch_norm_params, dropout_mask={}):
u = {}
un = {}
z = {}
# 入力層
#z[0] = x
z[0] = calc_input(x, regularization_params, dropout_mask.get(0))
# 中間層
for i in range(1, layer):
u[i] = calc_affine(z[i-1], W[i], b[i])
#z[i] = middle_func(u[i], middle_params)
un[i], z[i] = calc_middle(u[i], middle_func, middle_params, regularization_params, batch_norm_params["batch_norm_gamma"][i], batch_norm_params["batch_norm_beta"][i], dropout_mask.get(i))
# 出力層
u[layer] = calc_affine(z[layer-1], W[layer], b[layer])
y = output_func(u[layer], output_params)
return u, un, z, y
# 逆伝播
def back_propagation(layer, u, un, z, y, t, W, b, middle_back_func, middle_params, output_error_back_func, regularization_params, batch_norm_params, dropout_mask={}):
du = {}
dz = {}
dW = {}
db = {}
batch_norm_dparams = {}
batch_norm_dparams["batch_norm_dgamma"] = {}
batch_norm_dparams["batch_norm_dbeta"] = {}
# 出力層
du[layer] = output_error_back_func(y, u[layer], t)
dz[layer-1], dW[layer], db[layer] = calc_affine_back(du[layer], z[layer-1], W[layer], b[layer], regularization_params)
# 中間層
for i in range(layer-1, 0, -1):
#du[i] = middle_back_func(dz[i], u[i], z[i], middle_params)
du[i], batch_norm_dparams["batch_norm_dgamma"][i], batch_norm_dparams["batch_norm_dbeta"][i] = calc_middle_back(dz[i], u[i], un[i], z[i], middle_back_func, middle_params, regularization_params, batch_norm_params["batch_norm_gamma"][i], batch_norm_params["batch_norm_beta"][i], dropout_mask.get(i))
dz[i-1], dW[i], db[i] = calc_affine_back(du[i], z[i-1], W[i], b[i], regularization_params)
return du, dz, dW, db, batch_norm_dparams
パラメータです。
| パラメータ | 既定値 | パラメータ値 |
|---|---|---|
| 中間層ノード数 | [100,50] | - |
| 重み初期化関数 | he_normal | lecun_normal,lecun_uniform, glorot_normal,glorot_uniform, he_normal,he_uniform, normal_w,uniform_w, zeros_w,ones_w |
| 重み初期化関数パラメータ | - | normal_wの場合、"mean"、"var" uniform_wの場合、"min"、"max" |
| バイアス初期化関数 | zeros_b | normal_b,uniform_b, zeros_b,ones_b |
| バイアス初期化関数パラメータ | - | normal_bの場合、"mean"、"var" uniform_bの場合、"min"、"max" |
| 学習率 | 0.1 | - |
| バッチサイズ | 100 | - |
| エポック数 | 50 | - |
| データ正規化関数 | min_max | min_max,z_score |
| データ正規化関数パラメータ | - | "axis":0、"axis":None |
| 中間層活性化関数 | relu | sigmoid,tanh,relu,leaky_relu, identity,softplus,softsign,step |
| 中間層活性化関数パラメータ | - | leaky_reluの場合、"alpha" |
| 出力層活性化関数 | softmax | softmax,identity |
| 出力層活性化関数パラメータ | - | - |
| 損失関数 | cross_entropy_error | mean_squared_error,cross_entropy_error |
| 最適化関数 | SGD | SGD,Momentum,Nesterov,AdaGrad,RMSProp,Adadelta,Adam |
| 最適化関数パラメータ | - | Momentum,Nesterovの場合、"mu" RMSProp,Adadeltaの場合、"gamma" Adamの場合、"beta1","beta2" AdaGrad,RMSProp,Adadelta,Adamの場合、"epsilon" |
| 正則化パラメータ | - | "weight_decay_func":L1_norm,L2_norm "weight_decay_lambda":重み定数 "dropout_input_ratio":入力層に対するドロップアウト率 "dropout_middle_ratio":中間層に対するドロップアウト率 "batch_norm":バッチ正規化有無(True,False) "batch_norm_eta":バッチ正規化学習率 |
| 学習データシャフルフラグ | True | True,False |
import numpy as np
import time
# 学習
def learn(
name, # 学習識別名
x_train, # 学習データ
t_train, # 学習正解
x_test, # テストデータ
t_test, # テスト正解
md=[100, 50], # 中間層ノード数
weight_init_func=he_normal, # 重み初期化関数
weight_init_params={}, # 重み初期化関数パラメータ
bias_init_func=zeros_b, # バイアス初期化関数
bias_init_params={}, # バイアス初期化関数パラメータ
eta=0.1, # 学習率
batch_size=100, # バッチサイズ
epoch=50, # エポック数
data_norm_func=min_max, # データ正規化関数
data_norm_params={}, # データ正規化関数パラメータ
middle_func=relu, # 中間層活性化関数
middle_params={}, # 中間層活性化関数パラメータ
output_func=softmax, # 出力層活性化関数
output_params={}, # 出力層活性化関数パラメータ
error_func=cross_entropy_error, # 損失関数
optimizer_func=SGD, # 最適化関数
optimizer_params={}, # 最適化パラメータ
regularization_params={}, # 正則化パラメータ
shuffle_flag=True # 学習データシャフルフラグ
):
# 学習識別名表示
print(name)
# ノード数
d = [x_train.shape[x_train.ndim-1]] + md + [t_train.shape[t_train.ndim-1]]
# 階層数
layer = len(d) - 1
# 重み、バイアスの初期化
W = {}
b = {}
for i in range(layer):
W[i+1] = weight_init_func(d[i], d[i+1], weight_init_params)
for i in range(layer):
b[i+1] = bias_init_func(d[i+1], bias_init_params)
# 入力データの正規化
stats = {}
nx_train, train_stats = data_norm_func(x_train, stats, data_norm_params)
nx_test, test_stats = data_norm_func(x_test, train_stats, data_norm_params)
# 正解率、誤差初期化
train_rate = np.zeros(epoch+1)
test_rate = np.zeros(epoch+1)
train_err = np.zeros(epoch+1)
test_err = np.zeros(epoch+1)
# 勾配関数
middle_back_func = eval(middle_func.__name__ + "_back")
output_error_back_func = eval(output_func.__name__ + "_" + error_func.__name__ + "_back")
if "weight_decay_func" in regularization_params: # 重み減衰
regularization_params["weight_decay_back_func"] = eval(regularization_params["weight_decay_func"].__name__ + "_back")
# 最適化情報初期化
optimizer_statsW = {}
optimizer_statsb = {}
for i in range(layer):
optimizer_statsW[i+1] = {}
optimizer_statsb[i+1] = {}
# 正規化用、γ、β、学習率の初期化
batch_norm_params = {}
batch_norm_params["batch_norm_gamma"] = {}
batch_norm_params["batch_norm_beta"] = {}
for i in range(1, layer):
batch_norm_params["batch_norm_gamma"][i] = np.ones(d[i])
batch_norm_params["batch_norm_beta"][i] = np.zeros(d[i])
batch_norm_eta = eta
if "batch_norm_eta" in regularization_params:
batch_norm_eta = regularization_params["batch_norm_eta"]
optimizer_stats_gamma = {}
optimizer_stats_beta = {}
for i in range(1, layer):
optimizer_stats_gamma[i] = {}
optimizer_stats_beta[i] = {}
# 実行(学習データ)
u_train, un_train, z_train, y_train = propagation(layer, nx_train, W, b, middle_func, middle_params, output_func, output_params, regularization_params, batch_norm_params)
train_rate[0] = accuracy_rate(y_train, t_train)
train_err[0] = calc_error(y_train, t_train, W, error_func, regularization_params)
# 実行(テストデータ)
u_test, un_test, z_test, y_test = propagation(layer, nx_test, W, b, middle_func, middle_params, output_func, output_params, regularization_params, batch_norm_params)
test_rate[0] = accuracy_rate(y_test, t_test)
test_err[0] = calc_error(y_test, t_test, W, error_func, regularization_params)
# 正解率、誤差表示
print(" 学習データ正解率 = " + str(train_rate[0]) + " テストデータ正解率 = " + str(test_rate[0]) +
" 学習データ誤差 = " + str(train_err[0]) + " テストデータ誤差 = " + str(test_err[0]))
# 開始時刻設定
start_time = time.time()
for i in range(epoch):
# 学習データシャッフル
nx = nx_train
t = t_train
if shuffle_flag:
# データのシャッフル(正解データも同期してシャフルする必要があるため一度、結合し分離)
nx_t = np.concatenate([nx_train, t_train], axis=1)
np.random.shuffle(nx_t)
nx, t = np.split(nx_t, [nx_train.shape[1]], axis=1)
# 学習
for j in range(0, nx.shape[0], batch_size):
# ドロップアウトマスクの設定
dropout_mask = set_dropout_mask(d, regularization_params)
# Nesterovの場合
if optimizer_func == Nesterov:
for k in range(1, layer+1):
if "v" in optimizer_statsW[k]:
W[k] = W[k] + optimizer_params["mu"] * optimizer_statsW[k]["v"]
if "v" in optimizer_statsb[k]:
b[k] = b[k] + optimizer_params["mu"] * optimizer_statsb[k]["v"]
# 実行
u, un, z, y = propagation(layer, nx[j:j+batch_size], W, b, middle_func, middle_params, output_func, output_params,
regularization_params, batch_norm_params, dropout_mask)
# 勾配を計算
du, dz, dW, db, batch_norm_dparams = back_propagation(layer, u, un, z, y, t[j:j+batch_size], W, b, middle_back_func, middle_params, output_error_back_func,
regularization_params, batch_norm_params, dropout_mask)
# 重み、バイアスの調整
for k in range(1, layer+1):
W[k], optimizer_statsW[k] = optimizer_func(W[k], dW[k], eta, optimizer_params, optimizer_statsW[k])
b[k], optimizer_statsb[k] = optimizer_func(b[k], db[k], eta, optimizer_params, optimizer_statsb[k])
# バッチ正規化の調整
if regularization_params.get("batch_norm"):
for k in range(1, layer):
batch_norm_params["batch_norm_gamma"][k], optimizer_stats_gamma[k] = optimizer_func(batch_norm_params["batch_norm_gamma"][k], batch_norm_dparams["batch_norm_dgamma"][k], batch_norm_eta, optimizer_params, optimizer_stats_gamma[k])
batch_norm_params["batch_norm_beta"][k], optimizer_stats_beta[k] = optimizer_func(batch_norm_params["batch_norm_beta"][k], batch_norm_dparams["batch_norm_dbeta"][k], batch_norm_eta, optimizer_params, optimizer_stats_beta[k])
# 重み、バイアス調整後の実行(学習データ)
u_train, un_train, z_train, y_train = propagation(layer, nx_train, W, b, middle_func, middle_params, output_func, output_params, regularization_params, batch_norm_params)
train_rate[i+1] = accuracy_rate(y_train, t_train)
train_err[i+1] = calc_error(y_train, t_train, W, error_func, regularization_params)
# 重み、バイアス調整後の実行(テストデータ)
u_test, un_test, z_test, y_test = propagation(layer, nx_test, W, b, middle_func, middle_params, output_func, output_params, regularization_params, batch_norm_params)
test_rate[i+1] = accuracy_rate(y_test, t_test)
test_err[i+1] = calc_error(y_test, t_test, W, error_func, regularization_params)
# 正解率、誤差表示
print(str(i+1) + " 学習データ正解率 = " + str(train_rate[i+1]) + " テストデータ正解率 = " + str(test_rate[i+1]) +
" 学習データ誤差 = " + str(train_err[i+1]) + " テストデータ誤差 = " + str(test_err[i+1]))
# 終了時刻設定
end_time = time.time()
total_time = end_time - start_time
print("所要時間 = " +str(int(total_time/60))+" 分 "+str(int(total_time%60)) + " 秒")
return y_train, y_test, W, b, train_rate, train_err, test_rate, test_err, total_time
各手法を取り入れたためプログラムがかなり複雑になりました。次回、もう少し整理してみます。