ディープラーニングを実装から学ぶ（8-2）活性化関数(Swish,Mish)

活性化関数、Swish,Mishについて、MNISTにて精度を確認してみましょう。
プログラムは、「ディープラーニングを実装から学ぶ（8）実装変更」を利用します。

Swish

まずは、Swishです。
通常、sigmoidは、0～1の確率を表す場合以外、活性化関数に使われなくなっています。それが、単に、$ x $を掛けただけで復活です。まさに、sigmoidの逆襲。

f(x) = x\cdot\mathrm{sigmoid}(x)

グラフを表示してみます。
赤がSwishです。参考までに、ReLUを青で示します。
似ていますね。$ x=0 $の場合も滑らかです。

一般的に、ハイパーパラメータ$ \beta $を利用するようです。以下の式になります。

f_{swish}(x) = x\cdot\mathrm{sigmoid}(\beta x)

関数の定義です。

def swish(u, beta=1):
    return u * sigmoid(beta*u)

ネットワーク図

勾配計算用にネットワーク図を描きます。

ネットワーク図の書き方は以下にまとめていますので参照してください。
ディープラーニングを実装から学ぶ（4-2）学習（誤差逆伝播法２） ネットワーク図の書き方

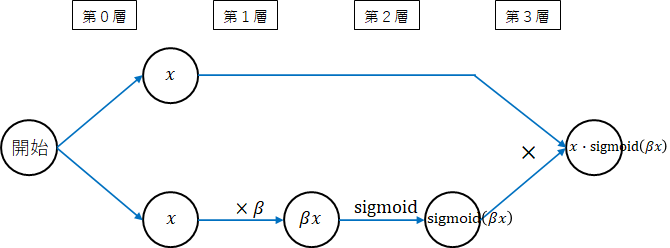
ネットワーク図を描いてみます。

第0層から順番に演算を行えば、Swishの式になります。

勾配計算

勾配を計算していきます。勾配を計算するための法則を以下にまとめていますので参照してください。
ディープラーニングを実装から学ぶ（4-2）学習（誤差逆伝播法２） 法則まとめ

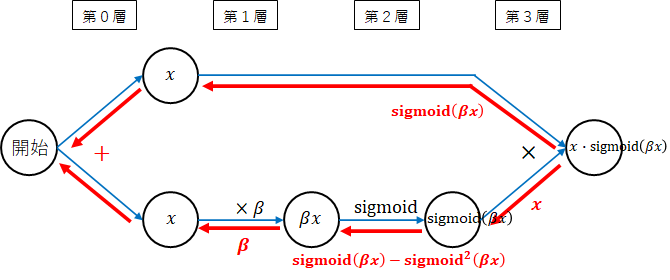
• 第3層 $ \times $
  掛け算は、それぞれ逆の値を返します。上段には、$ \mathrm{sigmoid}(\beta x) $、下段には、$ x $が返されます。

• 第2層 $ \mathrm{sigmoid} $
  $ \mathrm{sigmoid} $ の勾配は、以下でした。
  ディープラーニングを実装から学ぶ（5）学習（パラメータ調整） sigmoid

\mathrm{sigmoid}'(x) = \mathrm{sigmoid}(x) - \mathrm{sigmoid}^2(x)

ここでは、以下となります。

\mathrm{sigmoid}'(\beta x) = \mathrm{sigmoid}(\beta x) - \mathrm{sigmoid}^2(\beta x)

• 第1層　$ \times \beta $
  ここは、$ \beta $ですね。

• 全体の勾配
  上段、下段をそれぞれ後ろから掛けていき最後に加えます。

\begin{align}
f_{swish}'(x) &= \mathrm{sigmoid}(\beta x) + x\cdot(\mathrm{sigmoid}(\beta x) - \mathrm{sigmoid}^2(\beta x))\cdot\beta\\
              &= \mathrm{sigmoid}(\beta x) + \beta\cdot x\cdot \mathrm{sigmoid}(\beta x) - \beta\cdot x\cdot\mathrm{sigmoid}(\beta x)\cdot\mathrm{sigmoid}(\beta x)\\
              &= \beta\cdot x\cdot \mathrm{sigmoid}(\beta x) + \mathrm{sigmoid}(\beta x)(1-\beta\cdot x\cdot \mathrm{sigmoid}(\beta x))
\end{align}

$ x\cdot \mathrm{sigmoid}(\beta x) $がSwishの式でした。最終的には、以下の式になります。

f_{swish}'(x) = \beta\cdot f_{swish}(x) + \mathrm{sigmoid}(\beta x)(1-\beta\cdot f_{swish}(x))

逆伝播の関数は、後ろからの勾配($ dz $)を掛けます。$ z $がSwish関数後の値です。

def swish_back(dz, u, z, beta=1):
    return dz * (beta*z + sigmoid(beta*u) * (1 - beta*z))

Mish

次に、Mishです。
こちらも、tanh、softplusといった今までの活性化関数を組み合わせたもの。次の式で表せます。

f_{mish}(x) = x\cdot\mathrm{tanh}(\mathrm{softplus}(x))

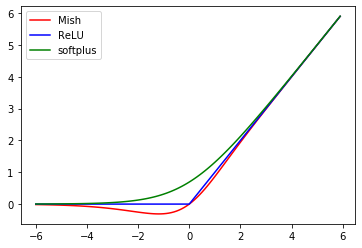
グラフを表示してみます。
赤がMishです。参考までに、ReLUを青、softplusを緑で示します。
Swishと似ていますね。

関数の定義です。

def mish(u):
    return u * tanh(softplus(u))

ネットワーク図

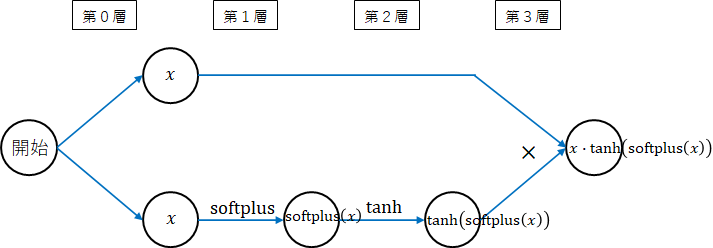
勾配計算用にネットワーク図を描きます。

第0層から順番に演算を行えば、Mishの式になります。

勾配計算

ネットワーク図に勾配を赤字で追加しました。

• 第3層 $ \times $
  掛け算は、それぞれ逆の値を返します。上段には、$ \mathrm{tanh}(\mathrm{softplus}(x)) $、下段には、$ x $が返されます。

• 第2層 $ \mathrm{tanh} $
  $ \mathrm{tanh} $ の勾配は、以下でした。
  ディープラーニングを実装から学ぶ（5）学習（パラメータ調整） tanh

\mathrm{tanh}'(x) = \frac{1}{\cosh^2(x)}

ここでは、以下となります。

\mathrm{tanh}'(\mathrm{softplus}(x)) = \frac{1}{\cosh^2(\mathrm{softplus}(x))}

• 第1層 $ \mathrm{softplus} $

$ \mathrm{softplus} $ の勾配は、以下でした。
ディープラーニングを実装から学ぶ（5）学習（パラメータ調整） softplus

\mathrm{softplus}'(x) = \frac{1}{1 + \exp(-x)}

• 全体の勾配

上段、下段をそれぞれ後ろから掛けていき最後に加えます。

\begin{align}
f_{mish}'(x) &= \mathrm{tanh}(\mathrm{softplus}(x)) + x\cdot\frac{1}{\cosh^2(\mathrm{softplus}(x))} \cdot \frac{1}{1 + \exp(-x)}\\
             &= \mathrm{tanh}(\mathrm{softplus}(x)) + \frac{x}{\cosh^2(\mathrm{softplus}(x)) \cdot(1 + \exp(-x))}
\end{align}

数学の力を借りれば、さらに展開できるかもしれませんが、このまま実装します。
逆伝播の関数は、後ろからの勾配($ dz $)を掛けます。

def mish_back(dz, u, z):
    return dz * (tanh(softplus(u)) + u / ((np.cosh(softplus(u))**2) * (1 + np.exp(-u))))

実行

MNISTの予測を行います。
プログラムは、「ディープラーニングを実装から学ぶ（8）実装変更」を利用します。

データの読み込み、正規化

x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
data_normalizer = create_data_normalizer(min_max)
nx_train, data_normalizer_stats = train_data_normalize(data_normalizer, x_train)
nx_test                         = test_data_normalize(data_normalizer, x_test)

Swish

モデル定義

model = create_model(nx_train.shape[1]) # 28*28
model = add_layer(model, "affine1", affine, 100)
model = add_layer(model, "swish1", swish)
model = add_layer(model, "affine2", affine, 50)
model = add_layer(model, "swish2", swish)
model = add_layer(model, "affine3", affine, 10)
model = set_output(model, softmax)
model = set_error(model, cross_entropy_error)

実行

epoch = 50
batch_size = 100
np.random.seed(10)
model, optimizer, learn_info = learn(model, nx_train, t_train, nx_test, t_test, batch_size=batch_size, epoch=epoch)

結果

input - 0 784
affine1 affine 784 100
swish1 swish 100 100
affine2 affine 100 50
swish2 swish 50 50
affine3 affine 50 10
output softmax 10
error cross_entropy_error
0 0.08016666666666666 2.363746423642613 0.08 2.361043337539476 
1 0.8661 0.46064354738936797 0.9258 0.2553879863817018 
2 0.93475 0.2230039954913801 0.9447 0.18268076204394698 
3 0.95115 0.16702682556963605 0.9509 0.15954958200054506 
4 0.9606 0.1342966810003576 0.9644 0.11631809541465293 
5 0.9659 0.11322773432792027 0.9662 0.10926317430352797 
6 0.9710166666666666 0.09747924429152449 0.9683 0.1011795086511917 
7 0.9741333333333333 0.0853329059377778 0.9726 0.08977974574132572 
8 0.9769666666666666 0.07714725064037706 0.9696 0.093595261086649 
9 0.9794166666666667 0.06863793935870843 0.974 0.08671516395342703 
10 0.98135 0.0620251783172052 0.976 0.08185185558433526 
11 0.9830833333333333 0.05640341238981132 0.9743 0.08100794823751652 
12 0.9847333333333333 0.05156579088833014 0.9756 0.08131250470300246 
13 0.9855166666666667 0.04674340506660428 0.9752 0.08052400110275582 
14 0.9874333333333334 0.04220652491761208 0.9747 0.07981868992533424 
15 0.9879333333333333 0.03915151090063953 0.976 0.07765970302716156 
16 0.9891333333333333 0.03651708203839035 0.9784 0.07349445764525939 
17 0.9898666666666667 0.032732107768213746 0.9767 0.07770710177089368 
18 0.9913833333333333 0.029932876124755484 0.9797 0.07239767739749721 
19 0.99215 0.027302186524866694 0.9784 0.07510570541618404 
20 0.99345 0.02425028339281888 0.9786 0.07525033964837108 
21 0.9937 0.022317574169503758 0.9785 0.08005968569870989 
22 0.9945833333333334 0.02062276672682784 0.9782 0.07829790134869177 
23 0.9950833333333333 0.018790205816722454 0.9778 0.07855597963652612 
24 0.99585 0.017506090030908725 0.9764 0.08590036807199888 
25 0.9960833333333333 0.015643211113382037 0.9783 0.082724846904772 
26 0.9965833333333334 0.014029930173114553 0.9791 0.07954372679968114 
27 0.9971833333333333 0.012945376747945592 0.9794 0.07960255306396687 
28 0.9975 0.01212873644910683 0.9799 0.07918193084560168 
29 0.99785 0.010840051700853127 0.9787 0.08207121773273189 
30 0.9983 0.009436095649006772 0.9787 0.0817552623555077 
31 0.9984333333333333 0.008791480430661252 0.9794 0.08764973865689216 
32 0.99845 0.008320079015286594 0.9799 0.08124667790126622 
33 0.9987666666666667 0.007283694533541066 0.9804 0.08330667920169645 
34 0.9989833333333333 0.006726324140902366 0.9798 0.08446212623518219 
35 0.9992833333333333 0.005785263839019389 0.9795 0.08529440883580727 
36 0.9993166666666666 0.005478370288413576 0.9805 0.08338382774054603 
37 0.9993666666666666 0.004971546544273701 0.9803 0.08555232700701487 
38 0.99955 0.004537678315232474 0.98 0.08825540749385374 
39 0.9996 0.004067231101270751 0.9801 0.08706053776033114 
40 0.99965 0.003868719705630692 0.9787 0.08833443539642134 
41 0.9997666666666667 0.003546580316336657 0.9796 0.0876189398008612 
42 0.9996166666666667 0.0034797715036991835 0.9802 0.09008584790535891 
43 0.9997333333333334 0.003132835639477984 0.9796 0.09302519819110096 
44 0.9998333333333334 0.002725451143852413 0.9785 0.09411029036476322 
45 0.9998666666666667 0.002688153167269417 0.9802 0.09126698237747104 
46 0.9999166666666667 0.0024042953943552514 0.9793 0.09198003741548652 
47 0.99995 0.0022048878961061532 0.9791 0.09350637570487375 
48 0.9999333333333333 0.0021145261631664316 0.98 0.094079416226775 
49 0.9999333333333333 0.002001931045080624 0.9797 0.09436901555713144 
50 0.99995 0.00180863336627983 0.9801 0.09394037930276859 
所要時間 = 0 分 57 秒

以前使用していたPCが壊れたためPCを変更しています。
所要時間は、今までと比較はできません。

Mish

モデル定義

model = create_model(nx_train.shape[1]) # 28*28
model = add_layer(model, "affine1", affine, 100)
model = add_layer(model, "mish1", mish)
model = add_layer(model, "affine2", affine, 50)
model = add_layer(model, "mish2", mish)
model = add_layer(model, "affine3", affine, 10)
model = set_output(model, softmax)
model = set_error(model, cross_entropy_error)

実行

epoch = 50
batch_size = 100
np.random.seed(10)
model, optimizer, learn_info = learn(model, nx_train, t_train, nx_test, t_test, batch_size=batch_size, epoch=epoch)

結果

input - 0 784
affine1 affine 784 100
mish1 mish 100 100
affine2 affine 100 50
mish2 mish 50 50
affine3 affine 50 10
output softmax 10
error cross_entropy_error
0 0.08151666666666667 2.4037523354775208 0.082 2.4003957685983206 
1 0.8774833333333333 0.41790080382608236 0.9302 0.23938184901750306 
2 0.9391166666666667 0.20640023387310436 0.9497 0.16878053462787623 
3 0.9552333333333334 0.15356767637362354 0.9548 0.1471607738364921 
4 0.9631 0.12339537379869142 0.9674 0.10947421060112761 
5 0.9691333333333333 0.10363595504276302 0.9675 0.10273326653685169 
6 0.9730333333333333 0.08898340196738011 0.9694 0.09678001677911578 
7 0.9759 0.07761906645932058 0.9738 0.08607950415597156 
8 0.97915 0.06955065438451004 0.9711 0.09113253723189957 
9 0.9818333333333333 0.061568814641619646 0.9731 0.084380989964184 
10 0.98325 0.055343671186227024 0.9759 0.08037179086500004 
11 0.9848833333333333 0.05026898335870314 0.9753 0.0788063464347413 
12 0.9868666666666667 0.04524145117166644 0.975 0.07768190166147027 
13 0.9876666666666667 0.040722061789953946 0.9764 0.0772829146261348 
14 0.9889833333333333 0.03654187448495889 0.9757 0.07690479372611891 
15 0.99005 0.033787426851503065 0.9773 0.07614492060336328 
16 0.9911333333333333 0.030872100487721082 0.9782 0.0721669501982931 
17 0.9916833333333334 0.027877936058251233 0.9784 0.07429992153407994 
18 0.9932333333333333 0.025311173287383613 0.9793 0.0717571051841584 
19 0.9941166666666666 0.022800130665436364 0.9792 0.07249734421441703 
20 0.9949833333333333 0.020247608392808078 0.9797 0.0733102877737386 
21 0.9956 0.018290638688836482 0.9783 0.07669012021607567 
22 0.99615 0.016844588285851853 0.9794 0.0748983937868421 
23 0.9964 0.015411965964636625 0.9781 0.07741411833970854 
24 0.9969666666666667 0.014017846769359391 0.9768 0.08020843640445294 
25 0.9975666666666667 0.012437527753559751 0.9785 0.07891449199480255 
26 0.9977333333333334 0.011285041206095043 0.9782 0.07757116441957727 
27 0.9980833333333333 0.010440016103561312 0.9793 0.07837949252792843 
28 0.9982666666666666 0.009659662756303582 0.9792 0.07829026438035153 
29 0.9985 0.008576113289891262 0.9784 0.08087949530878186 
30 0.99905 0.0074735564411989785 0.9792 0.07940684038471066 
31 0.999 0.006992661602067676 0.9779 0.08419242742582511 
32 0.9990166666666667 0.006421484435671801 0.9788 0.0810643472110933 
33 0.9993 0.005772020466493438 0.9791 0.08324257571124453 
34 0.9994166666666666 0.0052846788724286746 0.9799 0.08405130763732199 
35 0.9995833333333334 0.0045738097800962834 0.979 0.08440248422383051 
36 0.9996166666666667 0.004338108101144668 0.979 0.08408357887292611 
37 0.9996333333333334 0.004077462883077115 0.9789 0.08475690910757308 
38 0.9998 0.0035519926367029034 0.9785 0.08822369381899234 
39 0.9998 0.0033283737937051814 0.9797 0.08654132452803268 
40 0.9998666666666667 0.0030851310313939613 0.9791 0.0878037533296221 
41 0.9998166666666667 0.002878800583576215 0.9787 0.08715194793046566 
42 0.9998 0.002743174303202022 0.9792 0.08925255368970071 
43 0.9999 0.002525438878030701 0.9785 0.09178759338810824 
44 0.9998833333333333 0.0023211972539036144 0.9785 0.09099400717259103 
45 0.9999 0.0022175646629906632 0.9793 0.08921514244233521 
46 0.99995 0.0020537885697445757 0.9795 0.0911813648480129 
47 0.9999833333333333 0.001910456704177235 0.9794 0.09137450763779162 
48 0.9999666666666667 0.0018282484498641234 0.9796 0.09171814324997568 
49 0.9999833333333333 0.001756531335415239 0.9792 0.09317978123488532 
50 0.9999833333333333 0.0016404613357147496 0.9789 0.09235424448091202 
所要時間 = 1 分 47 秒

関数が複雑な分、Swishに比べて時間がかかりました。

比較

基本の実行

50エポック後の学習データの正解率、テストデータの正解率、テストの最高正解率です。
また、テストの正解率が、95%,97%,98%を超えたエポック数を示します。
参考のため、ReLUも含めます。Swishの$ \beta $は、既定値の1です。

活性化関数	学習正解	テスト正解	テスト最高	TS95%	TS97%	TS98%
ReLU	100.00	97.85	97.88	2	5	-
Swish	100.00	98.01	98.05	3	7	33
Mish	100.00	97.89	97.99	3	7	-

若干、Swish,Mishが良くなりました。

Swishの$ \beta $を変更して実行します。

$ \beta $	学習正解	テスト正解	テスト最高	TS95%	TS97%	TS98%
0.5	99.92	97.79	97.98	4	11	-
1.0	100.00	98.01	98.05	3	7	33
2.0	100.00	97.96	98.00	2	6	30

学習係数変更

学習係数を0.5（既定値:0.1)に変更し確認します。

活性化関数	学習正解	テスト正解	テスト最高	TS95%	TS97%	TS98%
ReLU	100.00	98.07	98.12	1	3	22
Swish	100.00	98.07	98.13	1	4	17
Mish	100.00	98.24	98.26	1	2	11

この場合は、Mishが良くなりました。
テストデータの正解率の推移をグラフ化します。

ノード数変更

ノード数を100-50から200-100に拡大してみます。

活性化関数	学習係数	学習正解	テスト正解	テスト最高	TS95%	TS97%	TS98%
ReLU	0.1	100.00	98.01	98.08	2	5	26
Swish	0.1	99.99	98.10	98.15	3	6	17
Mish	0.1	100.00	98.15	98.21	2	6	16
ReLU	0.5	100.00	98.29	98.31	1	2	10
Swish	0.5	100.00	98.30	98.37	1	3	7
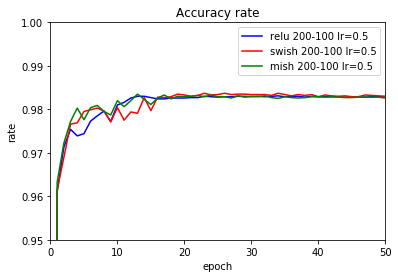
Mish	0.5	100.00	98.26	98.35	1	2	4

学習係数が0.5の場合のグラフです。

確認結果

Swish,Mishの正解率が若干高いようにも思えます。
ハイパーパラメータをもう少し調整すれば、さらに差異が明確になるかもしれません。
特に、Mishは、計算に時間がかかるので、性能上問題なければ、ReLUのかわりにMishを使ってみるのも良いかもしれません。

プログラム

今回追加したプログラムです。

# Swish
def swish(u, beta=1):
    return u * sigmoid(beta*u)
def swish_back(dz, u, z, beta=1):
    return dz * (beta*z + sigmoid(beta*u) * (1 - beta*z))

# Mish
def mish(u):
    return u * tanh(softplus(u))
def mish_back(dz, u, z):
    return dz * (tanh(softplus(u)) + u / ((np.cosh(softplus(u))**2) * (1 + np.exp(-u))))