性能改善は行えたものの、私の非力なノートPCだと、まだ、10エポックで30分程度かかります。本当は、いろいろパラメータを変更して試したかったのですが、その前に、新しい法則と数学の力を借りて改善することにしました。
勾配計算の改善
活性化関数
勾配を数値計算で求めていました。ここでは、数式で求める方法を考えます。
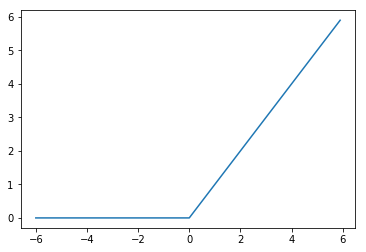
今回利用しているReLUを考えます。ReLUは、以下のような関数でした。
f(x) = \left\{
\begin{array}{ll}
x & (x \gt 0) \\
0 & (x \leq 0)
\end{array}
\right.
図で書くと以下のようになります。
$ x > 0 $ と $ x < 0 $ に分けて考えます。
- $ x > 0 $の場合、関数の値は、そのまま
\frac{f(x+h)-f(x-h)}{2h} = \frac{(x+h)-(x-h)}{2h} = \frac{2h}{2h} = 1
- $ x < 0 $の場合、関数の値は、0
\frac{f(x+h)-f(x-h)}{2h} = \frac{(0-0)}{2h} = 0
$ x = 0 $の場合は、数学的には、不定のようです。$ 0 $のところでかくっと折れ曲がってますからね。ここでは、計算しやすいように$ 0 $にしましょう。学習率などのパラメータによって、結果が大きく変わるので細かいことは気にしないです。まとめると勾配は、以下の式になります。ステップ関数と呼ばれる関数になります。
f^{'}(x) = \left\{
\begin{array}{ll}
1 & (x \gt 0) \\
0 & (x \leq 0)
\end{array}
\right.
実装です。関数名は、relu_backにしました。
def relu_back(x):
if x > 0:
return 1
else:
return 0
ただし、これだと配列の場合、一気に計算できません。少し手直しします。whereを使えば、条件により、値の場合分けができます。
def relu_back(x):
return np.where(x > 0, 1, 0)
出力層+損失関数
出力層の活性化関数には、softmax関数、損失関数は、交差エントロピー誤差を利用していました。それぞれ以下の関数です。
- softmax関数
f(x_i) = \frac{\exp(x_i)}{\sum_{k=1}^{n}\exp(x_k)}
- 交差エントロピー誤差
E(y) = -\sum_kt_k\log{y_k}
交差エントロピー誤差の勾配
まずは、交差エントロピー誤差から。
そのままだと勾配を計算できそうにないので法則3を使います。
** 法則3:複雑な関数は分解し、法則1、法則2を利用し勾配を求める。**
交差エントロピー誤差を$ y $の変形順に層として考えてみましょう。
第1層:$ y_i $の$ log $を取ります。
x_i^{(1)} = f^{(1)}(y_i) = \log(y_i)
第2層:$ t_i $を掛けます。
x_i^{(2)} = f^{(2)}(x_i^{(1)}) = t_i \times x_i^{(1)}
第3層:$ x_i^{(2)} $をすべて加えます。
S^{(3)} = f^{(3)}(x^{(2)}) = \sum_kx_k^{(2)}
第4層:$ -1 $を掛けます。
E = E(S^{(3)}) = -1 \times S^{(3)}
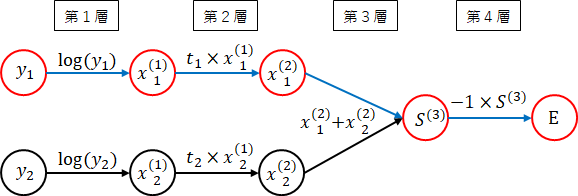
層の順番に実行すると、交差エントロピー誤差が求められます。ばらばらに書くとわかりにくいですね。
ネットワーク図に書いて整理します。(ネットワーク図の作り方は、法則まとめに書いています。)
では、勾配を後ろから順番に求めます。
第4層:$ -1 $を掛けた場合の勾配
E^{'}(S^{(3)}) = \frac{(-1 \times (S^{(3)}+h))- (-1 \times (S^{(3)}-h))}{2h} = \frac{-2h}{2h} = -1
第4層の勾配は、$ -1 $です。
一般に定数($ a $)を掛けた場合、以下になります。
f(x) = ax
```
勾配を計算します。
````math
f^{'}(x) = \frac{a(x+h) - a(x+h)}{2h} = \frac{2ah}{2h} = a
```
勾配は、定数部分になりました。
ついでに定数($ a $)を加えた場合も計算します。
````math
\begin{align}
f(x) &= x + a\\
f^{'}(x) &= \frac{((x + h) + a) - ((x - h) + a)}{2h} = \frac{2h}{2h} = 1
\end{align}
```
定数を加えた場合は、$ 1 $になりました。
** 法則3($ + $定数):定数を加えた場合の勾配 $ = 1 $**
** 法則3($ \times $定数):定数を掛けた場合の勾配 $ = $定数**
(微分がわかれば、あえて書く必要もないことですが)
第3層:$ x_i^{(2)} $をすべて加えた場合の勾配
$ x_1^{(2)} $の場合を考えてみます。
```math
f^{'(3)}(x_1^{(2)}) = \frac{((x_1^{(2)} + h) + x_2^{(2)}) - ((x_1^{(2)} - h) + x_2^{(2)})}{2h} = \frac{2h}{2h} = 1
```
1になりました。$ x_2^{(2)} $も同様に1になります。
一般的にも以下が言えます。
```math
\begin{align}
f(x) &= \sum_kx_k\\
f^{'}(x_i) &= 1
\end{align}
```
** 法則3($ \sum $):$ \sum $の勾配 $ = 1 $**
(こちらも偏微分がわかれば、自明ですが)
第2層:$ t_i $を掛けた場合の勾配
法則3($ \times $定数)から勾配は、$ t_i $になります。
第1層:$ \log $の勾配
これは、あっさりあきらめて数学の力を借りましょう。$ \log $の勾配は、以下のようになります。
(対数の微分で調べてください)
```math
\begin{align}
f(x) &= \log(x)\\
f^{'}(x) &= \frac{1}{x}
\end{align}
```
勾配は、以下のように、$ \frac{1}{y_i} $になります。
```math
f^{'(1)}(y_i) = \frac{1}{y_i}
```
** 法則3(関数):関数の勾配は、数学の力を借りる**
全層:全体の勾配を計算
求めた勾配を対象の矢印部分に赤字で記入しました。

法則1から各勾配を順番にかければよいのでした。$ y_1 $の勾配は、赤矢印の部分です。全体の勾配を求めてみます。後ろの勾配から順に掛けます。
```math
f{'}(y_1) = -1 \times 1 \times t_1 \times \frac{1}{y_1} = -\frac{t_1}{y_1}
```
$ y_2 $も同様に、$ -\frac{t_2}{y_2} $になります。
一般的には、以下となります。
```math
f{'}(y_i) = -\frac{t_i}{y_i}
```
### softmax関数の勾配
次は、softmax関数です。分子と分母に$ x_i $が含まれます。分子と分母で分岐が発生し複雑になります。
第1層:$ e $を$ x_i $乗します。
```math
x_i^{(1)} = f^{(1)}(x_i) = \exp(x_i)
```
次に分子と分母を分けて考えます。分子は、そのままなので、分母について考えます。
第2層:$ x_i^{(1)} $をすべて加えます。
```math
S^{(2)} = f^{(2)}(x^{(1)}) = \sum_kx_k^{(1)}
```
第3層:分母とするため逆数をとります。
```math
S^{(3)} = f^{(3)}(S^{(2)}) = \frac{1}{S^{(2)}}
```
第4層:分子と分母を掛けます。
```math
y_i = f^{(4)}(x_i^{(1)},S^{(3)}) = x_i^{(1)} \times S^{(3)}
```
ネットワーク図に書いてみます。分岐と結合があります。青矢印は、$ x_1 $の影響を示します。

それでは、後ろから順に勾配を求めて行きます。
第4層:掛け算の勾配
いきなり掛け算です。分子と分母に分けて考えます。
分子側
```math
\begin{align}
f^{'(4)}(x_1^{(1)}) &= \frac{((x_1^{(1)}+h) \times S^{(3)}) - ((x_1^{(1)}-h) \times S^{(3)})}{2h} &= \frac{2h \times S^{(3)}}{2h} = S^{(3)}
\end{align}
```
分母側
```math
\begin{align}
f^{'(4)}(S^{(3)}) &= \frac{(x_1^{(1)} \times (S^{(3)}+h)) - (x_1^{(1)} \times (S^{(3)}-h))}{2h} &= \frac{2h \times x_1^{(1)}}{2h} = x_1^{(1)}
\end{align}
```
分子側の勾配が、$ S^{(3)} $、分母側の勾配が、$ x_1^{(1)} $となりました。分子と分母の逆の値が勾配になりました。
一般的に以下になります。
```math
\begin{align}
f(x,y) &= xy\\
f^{'}(x) &= \frac{(x+h)y - (x-h)y}{2h} = \frac{2hy}{2h} = y\\
f^{'}(y) &= \frac{x(y+h) - x(y+h)}{2h} = \frac{2hx}{2h} = x
\end{align}
```
** 法則3($ \times $):2つの変数の掛け算の勾配は、それぞれ逆の変数となる**
第3層:$ \frac{1}{x} $の勾配
これもあきらめて数学の力を借りましょう。$ \frac{1}{x} $の勾配は、以下のようになります。
(分数の微分で調べてください)
```math
\begin{align}
f(x) &= \frac{1}{x}\\
f^{'}(x) &= -\frac{1}{x^2}
\end{align}
```
勾配は、以下のように、$ -\frac{1}{S^{(2)2}} $になります。
```math
f^{'(3)}(S^{(2)}) = -\frac{1}{S^{(2)2}}
```
第2層:$ x_i^{(1)} $をすべて加えた場合の勾配
法則3($ \sum $)より、勾配は、1ですね。
第1層:$ \exp $の勾配
これも数学の力ですね。$ \exp(x) $の勾配は、まったく同じ$ \exp(x) $になります。不思議な性質ですね。
(指数の微分で調べてください)
```math
f(x) = e^x\\
f^{'}(x) = e^x
```
勾配は、以下のように、$ \exp(x_i) $になります。
```math
f^{'(1)}(x_i) = \exp(x_i)
```
全層:全体の勾配を計算
求めた勾配を対象の矢印部分に赤字で記入しました。赤矢印部分が、$ x_1 $の勾配計算に関係します。

今回は、法則2も使います。分岐が交わる際には、両方を足せばよいですね。ただし、第四層については、$ y_1 $、$ y_2 $側がありますので、softmax関数部分だけの勾配は求められません。その先の損失関数に当たる$ f^{'}(y_1) $、$ f^{'}(y_2) $も計算に含めます。
分子部分と分母部分を求めて足して$ \exp $を掛ければよいですね。
分子部分
```math
f^{'}(y_1) \times S^{(3)}
```
分母部分
```math
((f^{'}(y_1) \times x_1^{(1)}) + (f^{'}(y_2) \times x_2^{(1)})) \times -\frac{1}{S^{(2)2}} \times 1
```
全体
```math
\begin{align}
f{'}(x_1) &= ((f^{'}(y_1) \times S^{(3)}) + (((f^{'}(y_1) \times x_1^{(1)}) + (f^{'}(y_2) \times x_2^{(1)})) \times -\frac{1}{S^{(2)2}} \times 1)) \times \exp(x_1)\\
&= f^{'}(y_2) \times S^{(3)} \times \exp(x_1) - \frac{((f^{'}(y_1) \times x_1^{(1)}) + (f^{'}(y_2) \times x_2^{(1)})) \times \exp(x_1)}{S^{(2)2}}
\end{align}
```
このままだと分かりにくいのでもとの定義に基づいて見直します。定義から以下が言えます。
```math
\begin{align}
S^{(3)} &= \frac{1}{S^{(2)}} = \frac{1}{\sum_kx_k^{(1)}} = \frac{1}{\sum_k\exp(x_k)}\\
S^{(2)} &= \sum_kx_k^{(1)} = \sum_k\exp(x_k)\\
x_i^{(1)} &= \exp(x_i)
\end{align}
```
これを前の式に当てはめてみます。
```math
\begin{align}
f{'}(x_1) &= f^{'}(y_1) \times S^{(3)} \times \exp(x_1) - \frac{((f^{'}(y_1) \times x_1^{(1)}) + (f^{'}(y_2) \times x_2^{(1)})) \times \exp(x_1)}{S^{(2)2}}\\
&= \frac{f^{'}(y_1) \times \exp(x_1)}{\sum_k\exp(x_k)} - \frac{((f^{'}(y_1) \times \exp(x_1)) + (f^{'}(y_2) \times \exp(x_2))) \times \exp(x_1)}{(\sum_k\exp(x_k))^2}\\
&= \frac{f^{'}(y_1) \times \exp(x_1)}{\sum_k\exp(x_k)} - ( \frac{f^{'}(y_1) \times \exp(x_1)}{\sum_k\exp(x_k)} + \frac{f^{'}(y_2) \times \exp(x_2)}{\sum_k\exp(x_k)} ) \times \frac{\exp(x_1)}{\sum_k\exp(x_k)}
\end{align}
```
どこかで見た形が並んでいます。そうです。$ y_i $です。
```math
y_i = \frac{\exp(x_i)}{\sum_k\exp(x_k)}
```
結局以下になります。
```math
f{'}(x_1) = f^{'}(y_1)y_1 - (f^{'}(y_1)y_1 + f^{'}(y_2)y_2)y_1
```
一般的には、以下になります。
```math
f{'}(x_i) = f^{'}(y_i)y_i - (\sum_kf^{'}(y_k)y_k)y_i
```
今回は、初めてなので、細かく変数を定義しました。分子と分母を定義する程度でよかったかも
分子を$ e_i $、分母を$ S $とします。
```math
\begin{align}
e_i &= \exp(x_i)\\
S &= \sum_k\exp(x_k)\\
y_i &= \frac{e_i}{S}
\end{align}
```

$ x_1 $勾配は、
```math
\begin{align}
f{'}(x_1) &= (\frac{f^{'}(y_1)}{S} + (((f^{'}(y_1) \times e_1) + (f^{'}(y_2) \times e_2)) \times -\frac{1}{S^2} \times 1)) \times e_1\\
&= \frac{f^{'}(y_1)e_1}{S} - (\frac{((f^{'}(y_1) \times e_1) + (f^{'}(y_2) \times e_2))e_1}{S} \times \frac{e_1}{S})\\
&= f^{'}(y_1)y_1 - (f^{'}(y_1)y_1 + f^{'}(y_2)y_2)y_1
\end{align}
```
少しすっきりしました。計算がややこしいですが、順番にゆっくり計算していけば大丈夫です。
### 全体の勾配
あとは、$ f^{'}(y_i) $の部分に交差エントロピー誤差の勾配を代入すればよいのですね。
交差エントロピー誤差の勾配は、以下でした。
```math
f{'}(y_i) = -\frac{t_i}{y_i}
```
全体の勾配は、以下となります。
```math
\begin{align}
f{'}(x_i) &= f^{'}(y_i)y_i - (\sum_kf^{'}(y_k)y_k)y_i\\
&= -\frac{t_iy_i}{y_i} - (\sum_k(-\frac{t_ky_k}{y_k}))y_i\\
&= (\sum_kt_k)y_i - t_i
\end{align}
```
ここで、$ t_i $は、正解が1、不正解が0でした。$ t_i $の総和は、$ 1 $になります。以下が成り立ちます。
```math
\sum_k(t_k) = 1
```
よって、以下となります。
```math
f{'}(x_i) = y_i - t_i
```
結局、非常に簡単な勾配になりました。逆に言えば、勾配が簡単になるように損失関数が決められているということですね。
前回の方法で本当に$y_i - t_i$となっているか確認してみます。
1番目のデータのy,t,y-t,du3を表示してみます。du3がy-tになっていればOKですね。
```python
if i == 0:
print(str(j+1) + " y[0] = " + str(y[0]))
print(str(j+1) + " t[0] = " + str(t[0]))
print(str(j+1) + " y[0]-t[0] = " + str(y[0]-t[0]))
print(str(j+1) + " du3[0] = " + str(du3[0]))
```
結果は、以下になりました。
```
1 y[0] = [ 0.06010029 0.13568082 0.2088617 0.06312099 0.10670362 0.0348616 0.06778975 0.10077724 0.10108594 0.12101804]
1 t[0] = [ 0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
1 y[0]-t[0] = [ 0.06010029 0.13568082 0.2088617 0.06312099 0.10670362 0.0348616 0.06778975 -0.89922276 0.10108594 0.12101804]
1 du3[0] = [ 0.000601 0.00135681 0.00208862 0.00063121 0.00106704 0.00034862 0.0006779 -0.00899223 0.00101086 0.00121018]
```
一致してそうなのですが、du3が1/100の値になりました。100と言えばバッチサイズ?バッチサイズを1にして再度実行します。
```
1 y[0] = [ 0.06010029 0.13568082 0.2088617 0.06312099 0.10670362 0.0348616 0.06778975 0.10077724 0.10108594 0.12101804]
1 t[0] = [ 0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
1 y[0]-t[0] = [ 0.06010029 0.13568082 0.2088617 0.06312099 0.10670362 0.0348616 0.06778975 -0.89922276 0.10108594 0.12101804]
1 du3[0] = [ 0.06010029 0.13568082 0.2088617 0.06312099 0.10670362 0.0348616 0.06778975 -0.89922276 0.10108594 0.12101804]
```
y-tとdu3が一致しました。
重みの勾配を求めることを考えてみましょう。
重みの勾配は、$ z $と$ du $を掛ければよかったですね。要素が2個で、ノード数が2の場合の重みを計算することを考えてみましょう。1データであれば以下ですね。
```math
\begin{pmatrix}
z_1 \\
z_2
\end{pmatrix}
\begin{pmatrix}
du_1 & du_2
\end{pmatrix}
=
\begin{pmatrix}
du_1z_1 & du_2z_1\\
du_1z_2 & du_2z_2
\end{pmatrix}
```
$ z $に、出力層の勾配($ du $)を掛けた結果になります。
バッチサイズが2の場合を考えてみましょう。右上の括弧内の数字は、何個目のデータかを表します。(1)は、1個目、(2)は、2個目です。
```math
\begin{pmatrix}
z_1^{(1)} & z_1^{(2)}\\
z_2^{(1)} & z_1^{(2)}
\end{pmatrix}
\begin{pmatrix}
du_1^{(1)} & du_2^{(1)}\\
du_1^{(2)} & du_2^{(2)}
\end{pmatrix}
=
\begin{pmatrix}
du_1^{(1)}z_1^{(1)}+du_1^{(2)}z_1^{(2)} & du_2^{(1)}z_1^{(1)}+du_2^{(2)}z_1^{(2)}\\
du_1^{(1)}z_2^{(1)}+du_1^{(2)}z_2^{(2)} & du_2^{(1)}z_2^{(1)}+du_2^{(2)}z_2^{(2)}
\end{pmatrix}
```
勾配は、各データの和になりました。バッチ数を増やすと大きな値になってしまいます。1個分の勾配とするために、バッチ数で割る必要があるのですね。
実は、交差エントロピー誤差関数の実装で、バッチサイズで割っていました。よって、ちゃんとバッチサイズで割った値となっていました。実装の時、気をつけねば。
```python
def cross_entropy_error(y, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return -np.sum(t * np.log(y))/size
```
### 勾配計算の実装
softmax関数と交差エントロピー誤差関数を合わせて、勾配を計算します。バッチサイズで割ることを忘れずに、
```python
def softmax_cross_entropy_error_back(y, x, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return (y - t)/size
```
## 実装見直し
今回、実装してきた勾配関数を組み込みます。
今までのmiddle_backを計算で求めるということでcalc_middle_backに変更します。同様に、output_error_backをcalc_output_error_backに変更します。middle_back、output_error_backは、後で、関数を変更できるようにしています。
```python
def relu_back(x):
return np.where(x > 0, 1, 0)
def softmax_cross_entropy_error_back(y, x, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return (y - t)/size
def middle_back(dz, x):
du = middle_back_func(x)
return dz * du
def calc_middle_back(dz, x):
h = 1e-4
work = x # 現在の値を一時退避
x = work + h # すこし大きな値
xph = middle_func(x)
x = work - h # すこし小さな値
xmh = middle_func(x)
du = (xph - xmh) / (2*h) # 勾配計算
x = work # 値をもとに戻す
return dz * du
def output_error_back(y, x, t):
return output_error_back_func(y, x, t)
def calc_output_error_back(y, x, t):
h = 1e-4
dx = np.zeros(x.shape)
for idx,i in np.ndenumerate(x):
work = x[idx] # 現在の値を一時退避
x[idx] = work + h # すこし大きな値
y = output_func(x)
xph = error_func(y, t)
x[idx] = work - h # すこし小さな値
y = output_func(x)
xmh = error_func(y, t)
dx[idx] = (xph - xmh) / (2*h) # 勾配計算
x[idx] = work # 値をもとに戻す
return dx
```
勾配計算関数を定義します。
```python
def middle_back_func(x):
return relu_back(x)
def output_error_back_func(y, x, t):
return softmax_cross_entropy_error_back(y, x, t)
```
今までの関数は、最後に、(参考)として記載します。まずは、そちらを実行してください。
output_error_backに勾配計算で$ y $が必要となったためパラメータを追加しました。その他は変更していません。早くなるはずなので、エポック数を100にしました。
```python
import numpy as np
# ノード数
d0 = 784
d1 = 50
d2 = 100
d3 = 10
# 重み、バイアスの初期化、学習率、バッチサイズ、エポックの設定
W1 = he_normal(d0,d1)
b1 = np.zeros(d1)
W2 = he_normal(d1,d2)
b2 = np.zeros(d2)
W3 = he_normal(d2,d3)
b3 = np.zeros(d3)
eta = 0.01
batch_size = 100
epoch = 100
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
# 入力データの正規化
z0_train = init_func(x_train)
z0_test = init_func(x_test)
# データのシャッフル(正解データも同期してシャフルする必要があるため一度、結合し分離)
z0_t = np.concatenate([z0_train, t_train], axis=1)
np.random.shuffle(z0_t)
z0, t = np.split(z0_t, [z0_train.shape[1]], axis=1)
# 実行(学習データ)
u1_train, z1_train, u2_train, z2_train, u3_train, y_train = propagation(z0_train)
# 実行(テストデータ)
u1_test, z1_test, u2_test, z2_test, u3_test, y_test = propagation(z0_test)
# 正解率表示
print(" 学習データ正解率 = " + str(accuracy_rate(y_train, t_train)) + " テストデータ正解率 = " + str(accuracy_rate(y_test, t_test)))
for j in range(epoch):
for i in range(0,z0.shape[0],batch_size):
# 実行
u1, z1, u2, z2, u3, y = propagation(z0[i:i+batch_size])
# 勾配を計算
du3 = output_error_back(y, u3, t[i:i+batch_size])
dz2, dW3, db3 = affine_back(du3, z2, W3, b3)
du2 = middle_back(dz2, u2)
dz1, dW2, db2 = affine_back(du2, z1, W2, b2)
du1 = middle_back(dz1, u1)
dz0, dW1, db1 = affine_back(du1, z0[i:i+batch_size], W1, b1)
# 重み、バイアスの調整
W1 = W1 - eta*dW1
b1 = b1 - eta*db1
W2 = W2 - eta*dW2
b2 = b2 - eta*db2
W3 = W3 - eta*dW3
b3 = b3 - eta*db3
# 調整後の実行(学習データ)
u1_train, z1_train, u2_train, z2_train, u3_train, y_train = propagation(z0_train)
# 調整後の実行(テストデータ)
u1_test, z1_test, u2_test, z2_test, u3_test, y_test = propagation(z0_test)
print(str(j+1) + " 学習データ正解率 = " + str(accuracy_rate(y_train, t_train)) + " テストデータ正解率 = " + str(accuracy_rate(y_test, t_test)))
```
100エポック約5分で実行できました。正解率は、97%までアップしました。
```
学習データ正解率 = 0.0955833333333 テストデータ正解率 = 0.0952
1 学習データ正解率 = 0.872316666667 テストデータ正解率 = 0.8748
2 学習データ正解率 = 0.897183333333 テストデータ正解率 = 0.9015
3 学習データ正解率 = 0.9101 テストデータ正解率 = 0.9106
4 学習データ正解率 = 0.91795 テストデータ正解率 = 0.9182
5 学習データ正解率 = 0.924533333333 テストデータ正解率 = 0.9228
6 学習データ正解率 = 0.929066666667 テストデータ正解率 = 0.928
7 学習データ正解率 = 0.93265 テストデータ正解率 = 0.9316
8 学習データ正解率 = 0.936066666667 テストデータ正解率 = 0.9356
9 学習データ正解率 = 0.939066666667 テストデータ正解率 = 0.9381
10 学習データ正解率 = 0.941283333333 テストデータ正解率 = 0.9405
途中省略
91 学習データ正解率 = 0.986833333333 テストデータ正解率 = 0.9729
92 学習データ正解率 = 0.986983333333 テストデータ正解率 = 0.9731
93 学習データ正解率 = 0.987083333333 テストデータ正解率 = 0.9731
94 学習データ正解率 = 0.987216666667 テストデータ正解率 = 0.9732
95 学習データ正解率 = 0.9874 テストデータ正解率 = 0.9733
96 学習データ正解率 = 0.987583333333 テストデータ正解率 = 0.9733
97 学習データ正解率 = 0.987783333333 テストデータ正解率 = 0.9733
98 学習データ正解率 = 0.9879 テストデータ正解率 = 0.9734
99 学習データ正解率 = 0.988033333333 テストデータ正解率 = 0.9734
100 学習データ正解率 = 0.988183333333 テストデータ正解率 = 0.9734
```
グラフに書くとこのようになりました。

# 法則まとめ
最後に法則をまとめます。
## 法則一覧
** 法則1:勾配は、ネットワークの各線の勾配の積となる。**
** 法則2:分岐の場合は、それぞれの勾配の和となる。**
** 法則3:複雑な関数は分解し、法則1、法則2を利用し勾配を求める。**
** ($ + $定数):定数を加えた場合の勾配 $ = 1 $**
** ($ \times $定数):定数を掛けた場合の勾配 $ = $定数**
** ($ \sum $):$ \sum $の勾配 $ = 1 $**
** ($ \times $):2つの変数の掛け算の勾配は、それぞれ逆の変数となる**
** (関数):関数の勾配は、数学の力を借りる**
## ネットワーク図の書き方
簡単な以下の関数で試してみます。
```math
f(x) = ax^2 + bx +c
```
第0層:分かりやすくするために第0層を設けました。$ x $が2つあるので、上下に$ x $ を書きます。関数中の変数を1列に書きます。
$ ax^2 $:上の$ x $は、$ ax^2 $の方とし、順番に見ていきましょう。まずは、$ x^2 $し、その次に$ a $を掛けます。順に右に第1層、第2層として書いていきます。
$ bx $:下の$ x $は、$ bx $とし、$ b $を掛けます。第1層として、右側に書きます。
第3層:次に、2つを加えるため結びます。
第4層:最後に、$ c $を足します。

勾配の計算は、上の法則を使えばよいですが、2乗のところは、以下に示します。
```math
\frac{(x+h)^2 - (x-h)^2}{2h} = \frac{4hx}{2h} = 2x
```
全体の勾配
```math
((2x \times a \times 1 ) + (b \times 1)) \times 1 = 2ax + b
```
みなさんは、ネットワーク図を書くこともなく、勾配(微分)は、$ 2ax + b $とわかりますよね。
## 割り算
割り算は、1度分母の逆数をとり、分子と掛けました。$ \frac{x}{y} $は、以下のようなネットワーク図になります。

勾配は、以下となります。
```math
\frac{1}{y} + ( -\frac{1}{y^2} \times x ) = \frac{y-x}{y^2}
```
割り算で直接計算する方法を考えてみましょう。
$ \frac{x}{y} $の勾配を分子と分母にわけて考えます。
分子の勾配
```math
\frac{\frac{(x+h)}{y}-\frac{(x-h)}{y}}{2h} = \frac{2h}{2hy} = \frac{1}{y}
```
分母の勾配
```math
\frac{\frac{x}{(y+h)}-\frac{x}{(y-h)}}{2h} = \frac{x(y-h) - x(y+h)}{2h(y+h)(y-h)} = \frac{-2hx}{2h(y^2-h^2)} = -\frac{x}{y^2-h^2}
```
ここで技を使います。$ h $は、小さい値でした。限りなく0に近いということで0とみなします。以下となります。
```math
-\frac{x}{y^2}
```
割り算($ \frac{x}{y} $)の勾配は、分子が、$ \frac{1}{y} $、分母が、$ -\frac{x}{y^2}$になりました。
割り算のネットワーク図です。

勾配は、以下となります。
```math
\frac{1}{y} -\frac{x}{y^2} = \frac{y - x}{y^2}
```
どちらも同じ結果ですね。逆数を取ってかけるか、割り算を使うか好きなほうを使ってください。
今度こそ、パラメータを変えて試してみます。
(参考)
```python
import gzip
import numpy as np
def load_mnist( mnist_path ) :
return _load_image(mnist_path + 'train-images-idx3-ubyte.gz'), \
_load_label(mnist_path + 'train-labels-idx1-ubyte.gz'), \
_load_image(mnist_path + 't10k-images-idx3-ubyte.gz'), \
_load_label(mnist_path + 't10k-labels-idx1-ubyte.gz')
def _load_image( image_path ) :
# 画像データの読み込み
with gzip.open(image_path, 'rb') as f:
buffer = f.read()
size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
rows = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=8)
columns = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=12)
data = np.frombuffer(buffer, np.uint8, offset=16)
image = np.reshape(data, (size[0], rows[0]*columns[0]))
image = image.astype(np.float32)
return image
def _load_label( label_path ) :
# 正解データ読み込み
with gzip.open(label_path, 'rb') as f:
buffer = f.read()
size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
data = np.frombuffer(buffer, np.uint8, offset=8)
label = np.zeros((size[0], 10))
for i in range(size[0]):
label[i, data[i]] = 1
return label
def min_max(x, axis=None):
x_min = np.min(x, axis=axis, keepdims=True) # 最小値を求める
x_max = np.max(x, axis=axis, keepdims=True) # 最大値を求める
return (x-x_min)/np.maximum((x_max-x_min),1e-7)
def z_score(x, axis = None):
x_mean = np.mean(x, axis=axis, keepdims=True) # 平均値を求める
x_std = np.std(x, axis=axis, keepdims=True) # 標準偏差を求める
return (x-x_mean)/np.maximum(x_std,1e-7)
def affine(z, W, b):
return np.dot(z, W) + b
def sigmoid(x):
return 1/(1 + np.exp(-x))
def tanh(x):
return np.tanh(x)
def relu(x):
return np.maximum(0, x)
def relu_back(x):
return np.where(x > 0, 1, 0)
def identity(x):
return x
def softmax(x):
x = x.T
max_x = np.max(x, axis=0)
exp_x = np.exp(x - max_x)
sum_exp_x = np.sum(exp_x, axis=0)
y = exp_x/sum_exp_x
return y.T
def lecun_normal(d_1, d):
std = 1/np.sqrt(d_1)
return np.random.normal(0, std, (d_1, d))
def lecun_uniform(d_1, d):
min = -np.sqrt(3/d_1)
max = np.sqrt(3/d_1)
return np.random.uniform(min, max, (d_1, d))
def glorot_normal(d_1, d):
std = np.sqrt(2/(d_1+d))
return np.random.normal(0, std, (d_1, d))
def glorot_uniform(d_1, d):
min = -np.sqrt(6/(d_1+d))
max = np.sqrt(6/(d_1+d))
return np.random.uniform(min, max, (d_1, d))
def he_normal(d_1, d):
std = np.sqrt(2/d_1)
return np.random.normal(0, std, (d_1, d))
def he_uniform(d_1, d):
min = -np.sqrt(6/d_1)
max = np.sqrt(6/d_1)
return np.random.uniform(min, max, (d_1, d))
def mean_squared_error(y, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return 0.5 * np.sum((y-t)**2)/size
def cross_entropy_error(y, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return -np.sum(t * np.log(y))/size
def softmax_cross_entropy_error_back(y, x, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return (y - t)/size
def calc_gradient(x, t, w):
h = 1e-4
gradient = np.zeros(w.shape)
for idx,i in np.ndenumerate(w): # すべてのデータに対して実行
work = w[idx] # 現在の値を一時退避
w[idx] = work + h # すこし大きな値
yph = propagation(x)
eph = error_func(yph, t)
w[idx] = work - h # すこし小さな値
ymh = propagation(x)
emh = error_func(ymh, t)
gradient[idx] = (eph - emh) / (2*h) # 勾配計算
w[idx] = work # 値をもとに戻す
return gradient
def accuracy_rate(y, t):
max_y = np.argmax(y, axis=1)
max_t = np.argmax(t, axis=1)
return np.sum(max_y == max_t)/y.shape[0]
def affine_back(dx, z, W, b):
dz = np.dot(dx, W.T) # zの勾配は、今までの勾配と重みを掛けた値
dW = np.dot(z.T, dx) # 重みの勾配は、zに今までの勾配を掛けた値
size = 1
if z.ndim == 2:
size = z.shape[0]
db = np.dot(np.ones(size).T, dx) # バイアスの勾配は、今までの勾配の値
return dz, dW, db
def middle_back(dz, x):
du = middle_back_func(x)
return dz * du
def calc_middle_back(x):
h = 1e-4
work = x # 現在の値を一時退避
x = work + h # すこし大きな値
xph = middle_func(x)
x = work - h # すこし小さな値
xmh = middle_func(x)
du = (xph - xmh) / (2*h) # 勾配計算
x = work # 値をもとに戻す
return du
def output_error_back(y, x, t):
return output_error_back_func(y, x, t)
def calc_output_error_back(y, x, t):
h = 1e-4
dx = np.zeros(x.shape)
for idx,i in np.ndenumerate(x):
work = x[idx] # 現在の値を一時退避
x[idx] = work + h # すこし大きな値
y = output_func(x)
xph = error_func(y, t)
x[idx] = work - h # すこし小さな値
y = output_func(x)
xmh = error_func(y, t)
dx[idx] = (xph - xmh) / (2*h) # 勾配計算
x[idx] = work # 値をもとに戻す
return dx
```
```
def propagation(x):
# 中間層(1)
u1 = affine(x, W1, b1)
z1 = middle_func(u1)
# 中間層(2)
u2 = affine(z1, W2, b2)
z2 = middle_func(u2)
# 出力層
u3 = affine(z2, W3, b3)
y = output_func(u3)
return u1, z1, u2, z2, u3, y
def init_func(x):
return min_max(x)
def middle_func(x):
return relu(x)
def middle_back_func(x):
return relu_back(x)
def output_func(x):
return softmax(x)
def error_func(y, t):
return cross_entropy_error(y, t)
def output_error_back_func(y, x, t):
return softmax_cross_entropy_error_back(y, x, t)
```