はじめに
この記事は2013年頃に、uGUIもなく、NGUIにお金を出すのも厳しかった時に、どうにかして円形のゲージを作りたくて作ったプログラムを、投稿用に手直しをしたものになります。
現在のUnityではuGUIでお手軽に実装できるのでそちらを使ったほうが確実に良いです。
UIではなく3D空間に表示したいだとか、Unityじゃない他のプログラムで実装するのには少し役立つかもしれません。
丸い画像はいらすとやさんからお借りしました。
お世話になってます。
丸のマークのイラスト「○」
実装
using UnityEngine;
[RequireComponent(typeof(MeshRenderer), typeof(MeshFilter))]
[ExecuteInEditMode]
public class CircleGauge : MonoBehaviour
{
private const float TWO_PI = Mathf.PI * 2;
private static readonly int[] Triangles = new int[]
{
4,3,5, 5,3,0,
3,2,0, 0,2,1,
5,0,6, 6,0,7,
0,9,7, 7,9,8,
};
private static readonly int[] TrianglesClockwise = new int[]
{
2,3,1, 1,3,0,
3,4,0, 0,4,5,
9,0,8, 8,0,7,
0,5,7, 7,5,6,
};
private enum StartPosition
{
Right = 0,
Top,
Left,
Bottom,
}
private Mesh _mesh = null;
private Vector3[] _vertices = null;
private Vector2[] _uv = null;
[SerializeField, Range(0.0f, 1.0f)]
private float _value = 0f;
[SerializeField]
private StartPosition _startPosition = StartPosition.Right;
[SerializeField]
private bool _clockwise = false;
[SerializeField]
private Texture2D _texture = null;
[SerializeField]
private bool _isUpdate = false;
void Start()
{
CreateMesh();
}
void Update()
{
if (_isUpdate)
{
_value += Time.deltaTime / 5;
if (_value > 1)
{
_value = _value - Mathf.Floor(_value);
}
}
UpdateMesh();
}
/// <summary>
/// Mesh情報更新
/// </summary>
private void UpdateMesh()
{
for (int i = 0; i < _vertices.Length; i++)
{
if (i != 0)
{
var val = Mathf.Clamp(_value, 0, 0.125f * (i - 1));
var rad = val * TWO_PI * (_clockwise ? -1 : 1) + Mathf.PI * ((int)_startPosition * 0.5f);
// normalized rad
rad = rad - TWO_PI * (int)(rad / TWO_PI);
if (rad < 0.0f)
{
rad += TWO_PI;
}
// rad in top
if (ValueInRange(rad, Mathf.PI * 0.25f, Mathf.PI * 0.75f))
{
_vertices[i].y = 0.5f;
_vertices[i].x = _vertices[i].y / Mathf.Tan(rad);
}
// rad in left
else if (ValueInRange(rad, Mathf.PI * 0.75f, Mathf.PI * 1.25f))
{
_vertices[i].x = -0.5f;
_vertices[i].y = Mathf.Tan(rad) * _vertices[i].x;
}
// rad in bottom
else if (ValueInRange(rad, Mathf.PI * 1.25f, Mathf.PI * 1.75f))
{
_vertices[i].y = -0.5f;
_vertices[i].x = _vertices[i].y / Mathf.Tan(rad);
}
// rad in right
else
{
_vertices[i].x = 0.5f;
_vertices[i].y = Mathf.Tan(rad) * _vertices[i].x;
}
}
_uv[i].x = _vertices[i].x + 0.5f;
_uv[i].y = _vertices[i].y + 0.5f;
}
_mesh.vertices = _vertices;
_mesh.uv = _uv;
_mesh.triangles = _clockwise ? TrianglesClockwise : Triangles;
}
/// <summary>
/// 値がmin~maxの範囲内にあるかチェック。
/// value が min, max と同じ値の場合もtrue。
/// </summary>
private bool ValueInRange(float value, float min, float max)
{
return min <= value && value <= max;
}
/// <summary>
/// 描画用Mesh生成
/// </summary>
[ContextMenu("Reset Mesh")]
private void CreateMesh()
{
var renderer = gameObject.GetComponent<MeshRenderer>();
var meshFilter = gameObject.GetComponent<MeshFilter>();
int length = 10;
_vertices = new Vector3[length];
_uv = new Vector2[length];
var material = new Material(Shader.Find("Mobile/Particles/Alpha Blended"))
{
name = "material"
};
material.SetTexture("_MainTex", _texture);
_mesh = meshFilter.sharedMesh = new Mesh();
renderer.sharedMaterial = material;
UpdateMesh();
}
}
解説
考え方
まず円形の画像を円形に表示したい場合はどうしたら良いかと考えたときに、中心点と円周上を360に分割した点でポリゴンを作れば良いかとも考えました。
ただ、少し重そうな気がしたのと、そのポリゴンに収まる余白のある元画像を作る必要がありそうだったのでもっと簡素化できないかと考えたときに、画像は四角形に描画されるので、四角形の外周を円運動と同じように角度によって等速で移動できないかと考えました。
上記のプログラムはそれをその通りに実装したものです。
四角形の外周を角度によって移動するには
※四角形のサイズは縦横1(0を中心としたxy共に-0.5~0.5の範囲)とします。
※角度は正規化されている(0~360°内にある)ものとします。
角度によってx,yのどちらかの値が決まる
まずは現在の角度によって、xまたyのどちらかの値が確定します。
- 角度が0°~45°、または225°~360°の時 : xは右辺上(0.5)に固定
- 角度が45°~135°の時 : yは常に上辺上(0.5)に固定
- 角度が135°~225°の時 : xは常に左辺上(-0.5)に固定
- 角度が225°~315°の時 : yは常に下辺上(-0.5)に固定
確定したxまたはyの値から、確定していないほうのx,yの値を算出
これにはTangentを用います。
覚えていますか?Tangent。
45°、135°、225°、315°に近いほど1または-1に近づき、水平に近いほど0、垂直に近いほど∞に近づきます。
式は tanθ = y / x です。
つまり
x が確定している場合 : y = tanθ * x
y が確定している場合 : x = y / tanθ
という風に確定した値から確定しいない方を算出します。
これで角度によって四角形のどの外周上にいるか算出できました。
Meshの作成と操作
必須コンポーネント
MeshRendererやMeshFilterなどのコンポーネントを用いて、自前でMeshの操作を行います。
[RequireComponent(typeof(MeshRenderer), typeof(MeshFilter))]
で描画に必要なコンポーネントが必ず付随するようにします。
Meshの作成
verticesとuvは、中心点+外周を移動する9つの点の計10点で構成します。
位置は後々計算で算出されるので初期化時はすべてVector3.zero(Vector2.zero)で大丈夫です。
こんなイメージです。
※振っている番号にも意味があります。
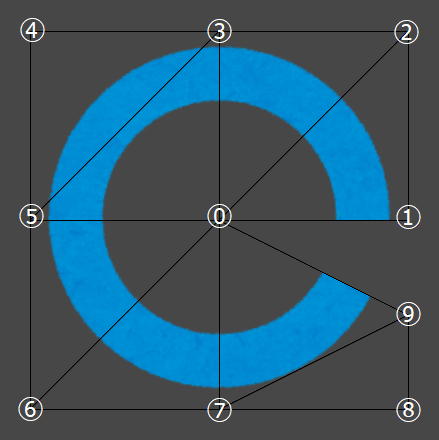
verticesの各点の位置
※右側を開始点とした場合の説明になります。
四角形の外周上の位置を角度によって決めることができましたが、次はそれをverticesの各点に反映します。
中心点は必ず(0,0)なので計算はスキップします。
それ以外の点ですが、入力された角度が何度であろうと各点の範囲は決まっているので、各点の計算時に角度をその点の最大値に制限する必要があります。
①の点は必ず0°、②の点は0°~45°、③の点は0°~90°... といった具合です。
それが
var val = Mathf.Clamp(_value, 0, 0.125f * (i - 1));
の部分です。
入力されるゲージの値 _value の値を制限することで、自動的に角度についても値が制限されることになります。
uvの各点の位置
uvについてはverticesの同じindexのx,y値に、それぞれ0.5をプラスした値が0~1になるのでそれで大丈夫です。
_uv[i].x = _vertices[i].x + 0.5f;
_uv[i].y = _vertices[i].y + 0.5f;
もしTexture全体ではなく、特定の範囲を使いたい等といった場合には、この値に範囲を掛け合わせて計算すればいけるはずです。
triangles
trianglesはカメラ側から見た際に、各ポリゴンが時計回りになるようになるように設定されていれば順番は特に関係ありません。
とりあえず左上から1枚ずつ三角形を構成するような作りにしています。
このコンポーネントでは反時計回り、時計回りを選べるようにしていますが、verticesの計算上、同じTrianglesを使ってしまうとゲージを時計回りにしたときにポリゴンが反時計回り(裏向き)になってしまうので、別々のTrianglesを用意しています。

その他余談的なもの
isUpdateフラグについて
_isUpdateのチェックはデバッグ用なので実際に使うときは消してください。
角度の正規化
rad = rad - TWO_PI * Mathf.Floor(rad / TWO_PI);
とすれば1行で書けますがほんの少しだけ処理速度が劣ります。
と言っても誤差程度なのでシビアな状況じゃなければこちらの方がスマートだと思います。
コメント // rad in right がif分の最後の分岐になっている理由
角度が右辺の範囲にあるかどうかの判定ですが、これをifで記述すると
if(ValueInRange(rad, Mathf.PI * 0, Mathf.PI * 0.25f) || ValueInRange(rad, Mathf.PI * 1.75f, Mathf.PI * 2.0f))
のようにこれだけ2回チェックになってしまうので意図的にelseにしてます。
最後に
最初にも書きましたが、UIとして使いたい場合はuGUIなどを使った方が良いです。
そちらだと360°以外にも180°、90°、Horizontal、Verticalなど色々なモードが選べます。
