C++ SSE/AVX 入門の記録

はじめに

Intelが考案したSSE/AVXという命令セットを利用することで、CPUで実行するコードのSIMD化によって高速化が図れます。
SIMD化はどういうものかから解説を始め、どうやってどのくらい高速化できたかなどを備忘録を兼ねて記していきます。
勉強中ゆえどうしても誤った記述をしてしまうかもしれません。見つけた方はコメントにて教えていただけると大変助かります！
また、この記事は Aizu Advent Calendar 2019 の5日目の記事です。
興味がある方は覗いてみてください。

想定読者

• 基本的なC/C++の文法が分かる方
• SIMDとかSSEって何？単語だけは耳にしたことあるけど...くらいの方。
• ごく基本的なCPU周辺のアーキテクチャを知っている方。CPUは演算ユニット、レジスタ、キャッシュがあってRAMと併せて値を読み書きしながら実行して... 程度がわかっていればOK

概観の説明

SISDとSIMD

CPUは実行ファイル(や、アセンブリプログラム)に記述された命令を読み込んで実行します。
SSE/AVXを利用しない通常の命令セットでは、1つのデータに対して1つの演算を行います。つまりフリンの分類で言うSISDというものです。
すると、CPUリソースが無駄になってしまうことがあります。
(2019/12/07追記) また任意の演算において、計算する必要のない領域が生まれることがあります。これではCPUリソースの無駄になってしまいます。

(注釈) 曖昧な書き方をしてしまっていたので訂正します。
「SISD演算が原因でCPUリソースが無駄になる」というわけではありません。

例えばこんな感じです。

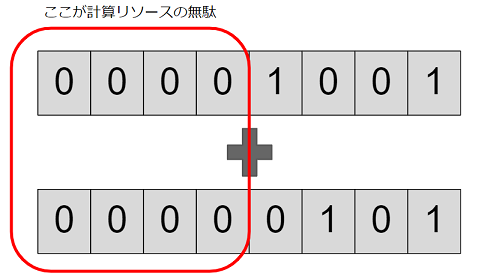
この無駄な部分を利用して、本来次のステップで演算される予定だった別のデータに対する演算をこのステップで同時に実行できるようにする、というのがSIMD演算のアイデアです。

SSE/AVX

CPUでのSIMD演算を可能にしたx86命令セットの拡張が、Intelが考案したSSE/AVXです。
それぞれ Streaming SIMD Extensions, Advanced Vector Extensionsといいます。AVXは後に考案されたSSEの後継バージョンです。
これらはそれぞれ128bitsのxmmレジスタ、256bitsのymmレジスタを利用して演算します。
このレジスタはSIMD演算のためにCPUへ組み込まれた追加のレジスタで、それ意外の用途には使われません。
ymmレジスタはymm0~ymm15の16個ぶんあります。xmmレジスタも同数で、ymmの半分の領域を共有して利用します。

C言語のIntrinsics

プログラマーがCPU命令セットを実行するよう記述するには普通アセンブリ言語でプログラムを書く必要がありますが、それをC言語から呼び出せるようにした組み込み関数が用意されています。
これらはIntrinsicsと呼ばれる関数群です。
SSE/AVXも同様にIntrinsicとしてC言語から実行できます。

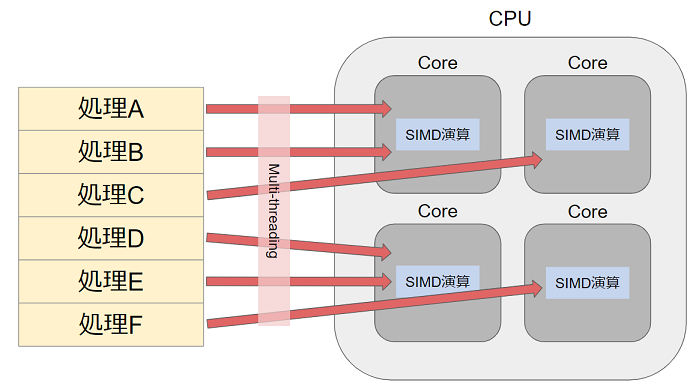
tip : 並列処理とSIMD演算の違い

並列処理は、1つの処理をCPUの複数のスレッドで分担させて行います。
対して、SIMD演算は複数のデータに対する1つの命令をCPUの1つのコア内のxmm/ymmレジスタで分担させて行います。

C++プログラムのSIMD化

C++によるIntrinsics実行

Intrinsicsを利用する際は、

1. メモリからxmm/ymmレジスタへ値をロード
2. レジスタ間演算
3. レジスタからメモリへ値をストア

という流れで実行します。これらはそれぞれ

__m256 _mm256_load_ps (float const * mem_addr)
__m256 _mm256_add_ps (__m256 a, __m256 b)
void _mm256_store_ps (float * mem_addr, __m256 a)

などの関数を呼び出すことで実行できます。
xmm/ymmレジスタに格納する値はuint8 * 32, float * 8, double * 4などプログラマーが好きに切って使えます。
そのため、各型に対応するIntrinsicsが大量に用意されています。
Intel® Intrinsics Guideがそのリファレンスサイトとなっているので、関数を探しながら書くのがよさそうです。

例 : ベクトルと行列の積

お膳立てが済んだところで、C++からのIntrinsics呼び出しによる高速化を試してみます。
要旨と関係ない部分のコードは冗長になるので割愛します。ご容赦を...

(筆者が書いたプログラム全体を見たい方はこちらのリポジトリへ)

Vector3f Multiply(const Vector3f& vec, const Matrix4x4& matrix) noexcept {
  return {
    vec.x * matrix[0][0] + vec.y * matrix[1][0] + vec.z * matrix[2][0] + matrix[3][0], // 乗算3回 + 加算3回
    vec.x * matrix[0][1] + vec.y * matrix[1][1] + vec.z * matrix[2][1] + matrix[3][1], // 乗算3回 + 加算3回
    vec.x * matrix[0][2] + vec.y * matrix[1][2] + vec.z * matrix[2][2] + matrix[3][2], // 乗算3回 + 加算3回
  };
}

Vector3f MultiplySimd(const Vector3f& vec, const Matrix4x4& matrix) noexcept {
  __m256 row01Reg = _mm256_load_ps(reinterpret_cast<const float*>(&(matrix[0])));
  __m256 row23Reg = _mm256_load_ps(reinterpret_cast<const float*>(&(matrix[2])));
  __m256 multFactorFor01 = _mm256_set_ps(vec.x, vec.x, vec.x, vec.x, vec.y, vec.y, vec.y, vec.y);
  __m256 multFactorFor23 = _mm256_set_ps(vec.z, vec.z, vec.z, vec.z, 1.0f, 1.0f, 1.0f, 1.0f);
  row01Reg = _mm256_mul_ps(row01Reg, multFactorFor01);  // 乗算1回
  row23Reg = _mm256_mul_ps(row23Reg, multFactorFor23);  // 乗算1回
  __m256 resultReg = _mm256_add_ps(row01Reg, row23Reg); // 加算1回
  alignas(32) float resultMem[8];
  _mm256_store_ps(reinterpret_cast<float*>(resultMem), resultReg);
  return { resultMem[0] + resultMem[4], resultMem[1] + resultMem[5], resultMem[2] + resultMem[6] }; // 加算3回
}

ざっくりカウントすると

• 普通に実装 : 乗算9回、加算9回
• SIMD化実装 : 乗算2回、加算4回 + ymmレジスタへのロード&ストアコスト

演算回数が少なくなっているので、高速化が期待できます。

ベンチマーク

前項の内容を含む時間計測の実装です。

#include "randomgenerator.hpp"
#include "stopwatch.hpp"
#include "vector3.hpp"
#include "vector4.hpp"
#include "matrix4x4.hpp"

#include <functional>
#include <iostream>
#include <string>
#include <vector>

template <class ReturnTy, class LhsTy, class RhsTy>
void Benchmark(const std::vector<LhsTy>& lhs, const std::vector<RhsTy>& rhs, const size_t numCalc, std::function<ReturnTy(const LhsTy&, const RhsTy&)> Func, const char* const benchName) {
  // 普通のストップウォッチ(中身はただのstd::chrono関連関数呼び出し)
  StopWatch stopwatch;
  stopwatch.Start();
  for (auto i = 0u; i < numCalc; ++i) {
    Func(lhs[i], rhs[i]);
  }
  stopwatch.Stop();
  std::cout << benchName << " : " << stopwatch.GetMicroseconds() << " microsec" << std::endl;
  stopwatch.Reset();
}

int main(int argc, char* argv[]) {
  // ベンチマーク対象の関数を実行する回数
  const auto numCalc = (argc > 1) ? std::stoul(argv[1]) : 100000;
  std::cout << "<<" << numCalc << " times calculations as Benchmark>>" << std::endl;

  // [-100.0, 100.0]の範囲の一様分布に準ずる疑似乱数生成器
  RandomGenerator rand;

  // 時間計測 : 3次元ベクトルの内積・外積
  {
    std::vector<Vector3f> vecA(numCalc);
    std::vector<Vector3f> vecB(numCalc);
    for (auto i = 0u; i < numCalc; ++i) {
      vecA[i] = { rand(),
                  rand(),
                  rand() };
    }
    Benchmark<float, Vector3f, Vector3f>(vecA, vecB, numCalc, Dot3D, "normal Vector3 Dot");
    Benchmark<float, Vector3f, Vector3f>(vecA, vecB, numCalc, Dot3DSimd, "SIMD Vector3 Dot");
    Benchmark<Vector3f, Vector3f, Vector3f>(vecA, vecB, numCalc, Cross3D, "normal Vector3 Cross");
    Benchmark<Vector3f, Vector3f, Vector3f>(vecA, vecB, numCalc, Cross3DSimd, "SIMD Vector3 Cross");
  }

  // 時間計測 : 4次元ベクトルの内積
  {
    std::vector<Vector4f> vecA(numCalc);
    std::vector<Vector4f> vecB(numCalc);
    for (auto i = 0u; i < numCalc; ++i) {
      vecA[i] = { rand(),
                  rand(),
                  rand(),
                  rand() };
    }
    Benchmark<float, Vector4f, Vector4f>(vecA, vecB, numCalc, Dot4D, "normal Vector4 Dot");
    Benchmark<float, Vector4f, Vector4f>(vecA, vecB, numCalc, Dot4DSimd, "SIMD Vector4 Dot");
  }

  // 時間計測 : 3次元ベクトルと4次元行列の積
  {
    std::vector<Vector3f> vec(numCalc);
    std::vector<Matrix4x4> matrices(numCalc);
    for (auto i = 0u; i < numCalc; ++i) {
      vec[i] = { rand(),
                 rand(),
                 rand() };
      matrices[i] = { { rand(), rand(), rand(), rand() },
                      { rand(), rand(), rand(), rand() },
                      { rand(), rand(), rand(), rand() },
                      { rand(), rand(), rand(), rand() } };
    }
    Benchmark<Vector3f, Vector3f, Matrix4x4>(vec, matrices, numCalc, Multiply, "normal Vector*Matrix");
    Benchmark<Vector3f, Vector3f, Matrix4x4>(vec, matrices, numCalc, MultiplySimd, "SIMD Vector*Matrix");
  }
}

実行結果:

g++ -O3 オプション

<<100000 times calculations as Benchmark>>
normal Vector3 Dot : 232 microsec
SIMD Vector3 Dot : 245 microsec
normal Vector3 Cross : 797 microsec
SIMD Vector3 Cross : 850 microsec
normal Vector4 Dot : 223 microsec
SIMD Vector4 Dot : 250 microsec
normal Vector*Matrix : 2179 microsec
SIMD Vector*Matrix : 1162 microsec

g++ -O0 オプション

<<100000 times calculations as Benchmark>>
normal Vector3 Dot : 2412 microsec
SIMD Vector3 Dot : 3280 microsec
normal Vector3 Cross : 4755 microsec
SIMD Vector3 Cross : 6964 microsec
normal Vector4 Dot : 2486 microsec
SIMD Vector4 Dot : 3172 microsec
normal Vector*Matrix : 9324 microsec
SIMD Vector*Matrix : 7598 microsec

3次元ベクトルの内積/外積程度の演算回数ではあまり高速化できないどころか、(おそらく)ロード&ストアのオーバーヘッドのせいで遅くなってしまうようです。
対して、演算回数の多いベクトルと行列の積では-O3で2倍、-O0で1.2倍程度高速化できているのがわかります。

実行環境など

CPU : AMD Ryzen 2700X
OS  : 18.04.3 LTS (Bionic Beaver)
compiler : gcc 7.4.0

注意点・ハマったところなど

データのアラインメント

lord元/store先になるメモリ領域がSSEなら16bytes-aligned, AVXなら32bytes-alignedになっていないとSegmentation Faultでプログラムが落ちる。

  __m128 left = _mm_set_ps(0.0f, 1.0f, 2.0f, 3.0f);
  __m128 right = _mm_set_ps(0.0f, 1.0f, 2.0f, 3.0f);
  __m128 resultReg = _mm_mul_ps(left, right);
  alignas(16) float resultMem[4];  // alignas(16)が無いと環境によってはセグる!!
  _mm_store_ps(reinterpret_cast<float*>(resultMem), resultReg);

分からないところ・疑問など

一通り触ってみて、記事執筆中に湧いた新たな疑問などを参考のため残します。
これらを解説する資料や技術書など,もしあればぜひコメントで教えてください！

• xmm/ymmレジスタはCPUの1コアにつき1セット(=16個のレジスタ)存在している？
• もし ↑ の通りならば、Intrinsicsを含むコードを実行する並列スレッド数(std::threadなどのインスタンス数)をCPUのコア数より多くすればxmm/ymmレジスタの値が破綻し得る？
• コンパイラの最適化は、可能な部分を自動でSIMD化してくれるのか？
• SSE/AVXのほかにFMAという命令セット拡張があり、SSE->AVXのようにサイズが増えたわけではないらしい。用途は何だろう？
• SSE/AVX Intrinsics利用時はプログラマーが手動でレジスタ-メモリ間のロード/ストアをするが、普段C++で普通に書く int n = a + b; のような演算もレジスタを利用して演算するはず。それらはどのような流れでレジスタに到達し、CPUのコアの演算ユニットで演算され、再びメモリに戻ってくるのか？
• 普通の演算、SIMD化演算問わずキャッシュはどのようにプログラム実行に関係してくるのか？

おわりに(感想)

少し前からx86アセンブリ言語を勉強すべきか？とは思っていましたが、SSE/AVX Intrinsicsに触れてみてその機運がとても高まりました。
ここまで読んでいただいた方、ありがとうございました。何かの参考になれば幸いです。

参考文献

Intel AVX を使用して SIMD 演算を試してみる
Intel AVX を使用して SIMD 演算を試してみる - その2 -
Introduction to Intel® Advanced Vector Extensions
Intel® Intrinsics Guide
組み込み関数（intrinsic）によるSIMD入門
SIMD - primitive: blog