DiceKriging in R を使ってみる

Last updated at 2025-12-06Posted at 2025-12-06

はじめに

近年、実験計画法の記事を読んでいるとAdaptive design of experimentsというものを目にします。日本語では適応的実験計画法とも呼ばれるようです。これを良い感じにやれそうなDiceKrigingというライブラリがあったので、触ってみています。
そこで、Krigingについて勉強しつつ、何回かに分けて整理していこうと思いますが、この記事はDiceKrigingを触ってみた最初の感触をまとめたものとなります。

この記事は、アドベントカレンダーに合わせて微修正を繰り返します。

適応的実験計画法について

適応型実験計画法について、まるっと引用しますが、以下の通りです。

適応的実験計画法は、実験の進行中に得られたデータをもとに、次の実験点を動的に決定していく手法です。このプロセスでは、次の実験候補をどのように生成するかが鍵となります。

私たち製造業では何かしらの目的をもって実験を行います。特定の物性値をコントロールする、たとえば「樹脂を固くする材料比率」みたいなものは、すでに経験的にわかっていたりするのですが、「収率を最大化する」みたいなものは、バランスを取る必要があり、どっかしらちょうどいい条件を探しに行くしかなかったりします。
このとき、EI（Expected Improvement、予測される期待値）が最大もしくは最小になる条件を取りに行くような形で、実験を半自動化出来たら良いよね、という考えがあり、その手法が適応型実験計画法と呼ばれているようです。

Krigingについて

クリギング(Kriging)というのは、元々は地球統計学で利用される手法であり、空間内挿手法のひとつです。実験計画法というのは、特定の次元の中で内挿しつつ、都合のよい条件を探す手法という側面があるためか、Krigingを用いた適応的実験計画法というものが提案されています。

DiceKrigingについて

という背景があって、良い感じのライブラリないかな～とAIに聞いたりしていて見つけたのが DiceKriging のファミリーです。 DiceKriging 、 DiceOptim 、 DiceDesign など目的に合わせて複数のライブラリがあります。

DiceKriging・・・Krigingでモデルを作成したりする
DiceOptim・・・作成したモデルを用いて最適条件を探索する。max_EIのようなEIを最大化する関数があって便利
DiceDesign・・・lhsDesign()のようなラテン超方格サンプリングなど様々なデザインを作成するライブラリ
DiceEval・・・作成したモデルを評価するライブラリ

さっそく使ってみよう

とりあえず、2つのライブラリを使って遊んでみます。

library(DiceKriging)
library(DiceOptim)

branin関数でテストしてみます。Branin関数というのは、最適化アルゴリズムの性能評価に広く使われる二変数のテスト関数で、3つのグローバル最小値を持ちます。この複雑な関数で、ちゃんと最適解にたどり着けるかを確認してみましょう。

> branin
function (x) 
{
    x1 <- x[1] * 15 - 5
    x2 <- x[2] * 15
    (x2 - 5/(4 * pi^2) * (x1^2) + 5/pi * x1 - 6)^2 + 10 * (1 - 
        1/(8 * pi)) * cos(x1) + 10
}

以下のコードで、モデルを作り、EI最小条件を探索してみます。

set.seed(0)

# 実験点は4*4点としてテスト
X <- expand.grid(x1 = seq(0, 1, length = 4), x2 = seq(0, 1, length = 4))
y <- apply(X, 1, branin)

# Krigingでモデル作成
m <- km( ~ ., design = X, response = y)

# EI最小条件の探索
res <- max_EI(
  model = m,
  upper = c(1, 1),
  lower = c(0, 0),
  minimization = TRUE
)

n.grid <- 50
x.grid <- seq(0, 1, length = n.grid)
X.grid <- expand.grid(x1 = x.grid, x2 = x.grid)
y.grid <- apply(X.grid, 1, branin)
pred.m <- predict(m, X.grid, "UK")

# Branin関数の等高線図
par(mfrow = c(1, 2))
contour(x.grid, x.grid, matrix(y.grid, n.grid, n.grid), 50, main = "Branin")
points(X[, 1],
       X[, 2],
       pch = 19,
       cex = 1.5,
       col = "red")

# Krigingモデルから予測した等高線図
contour(x.grid, x.grid, matrix(pred.m$mean, n.grid, n.grid), 50, main = "Kriging mean")
points(X[, 1],
       X[, 2],
       pch = 19,
       cex = 1.5,
       col = "red")
points(res$par[1],
       res$par[2],
       pch = 19,
       cex = 1.5,
       col = "blue")

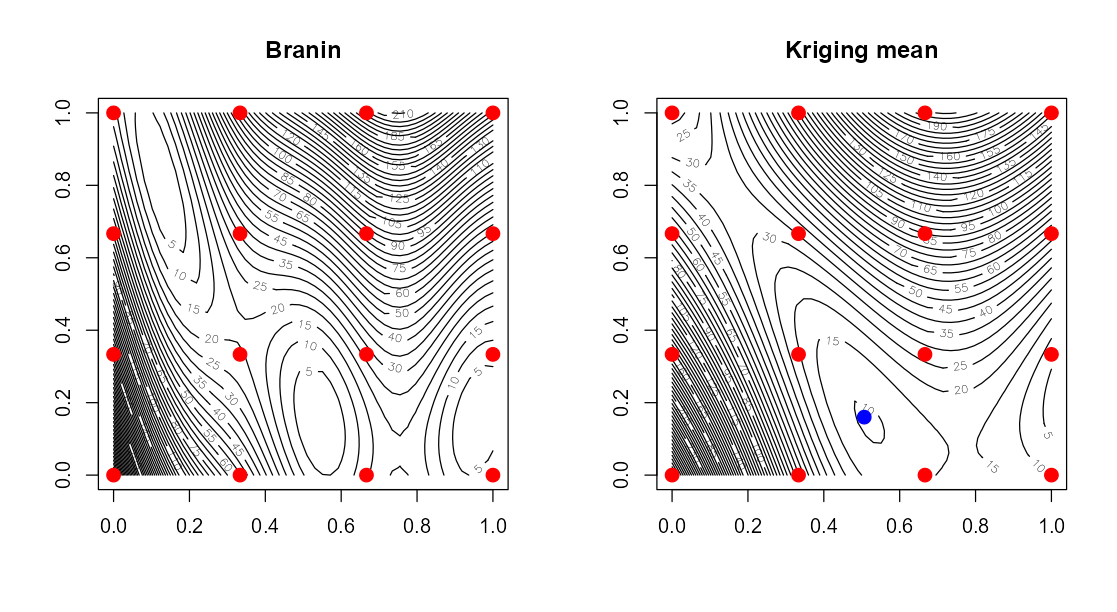
左のBraninのほうはBranin関数を50×50のグリッドで計算した結果を等高線で示したものです。右のKriging meanのほうは4×4(16点)の結果から0～1の範囲で予測した平均値を等高線で示したものです。
赤い点がKrigingモデルを作成するのに取得した点、青い点がmax_EI(minimization = TRUE)でyが最小点となると予測した点です。
こうしてみると、複雑な関数でもある程度全体を予測できており、最小点を狙えているようです。

> res
$par
            x1        x2
[1,] 0.5065342 0.1600005

$value
           EI
[1,] 4.886895

今後やること

DiceDesign でのサンプリング方法をまとめる
カーネルの違いについてまとめる
ハマったときどうするか
- たとえば、上の例でx1 = seq(0, 1, length = 2), x2 = seq(0, 1, length = 2)みたいなことをすれば当然最適化は出来ないのだが(length =3でもまあまあ怪しい)、次元が大きい際にちゃんと気付けるか、どう対処すればよいか、などをまとめる