素数探索プログラムを高速化しよう

これは 素数大富豪 Advent Calendar 2025 18日目の記事です。

昨日は y(ただのカービィ好き) さんによる 素数大富豪に出会ってからの10ヶ月の振り返り でした。記事内でワドルディと遊べて楽しかったです！
今日の記事はプログラミング系の話になります。

---

突然ですが、ぼっちざろっく第2話で、アルバイトを始めるかどうか葛藤しているぼっちちゃんがこんな独り言を言っています。

絶対嫌だ…。働きたくない怖い……社会が怖い！！

ぼっちちゃんはなぜ怖いのでしょうか？社会の一体何に怯えているのでしょうか？対人コミュニケーション？組織に評価されること？
…いえ、本質はそこではありません。ぼっちちゃんは自分の大好きなギターが、練習してうまくなった唯一の特技であるギターが、大人になって社会に出た時に自らを守ってくれず、自分が無力になってしまうことが怖いのです。

---

はじめまして。なかけんと申します。枠が空いていたので勧められる形でアドカレを書かせていただきました。

素数大富豪というゲームの存在自体は数年前から知っていましたが、最近になって3枚出し等をある程度覚え、今年2025年のマスぴよ杯で初めて大会参加させていただきました。色々と交流でき楽しい時間を過ごせました！

ちなみに5T1は「後藤ひとり素数」として覚えています。

最低限の自己紹介

私のバックグラウンドを書いておきます。

• 社会人(エンジニア)
• 大学での専門は応用数学¹² (端くれですが一応博士号を持っています)

私もぼっちちゃんと同様、特技が数学くらいしか思いつかないので、「数学」の後ろ盾を失った途端に社会では無力と化します。そこで「何としても数学を活かせる仕事に就かねば…！」と決意し、現在は仕事で

• 数値計算の高速化³ (物理シミュレーションを速くすること)

をしています。

数値計算なんていかにも高度な数学を活かせそうですが、実際はコンピュータサイエンスと物理学の方が重要で、若干の分野の違いはあります。
とはいえ、もちろん仕事で数学を活かせる場面もありますよ！例えば…………エクセルのSUM関数とかですかね。⁴

素数探索プログラム？？

今年2025年の札幌杯(の前夜祭)で はち と知り合いまして、色々と話す機会がありました。はちが、素数大富豪で出せる素数や合成数を探索するプログラム

を書いており、重い計算を回して色々な性質を調べていることを聞き、面白そうと思ったことを覚えています。

仕事でプログラムの高速化をやっていることもあり、コードの中身について色々と気になってしまい聞いてしまいました。素数大富豪特有の難しさとして

• 113等、出し方が複数通りある数
• ジョーカーの存在

などがありつつも、計算の効率が良くなるよう色々と工夫して実装されているようで、試行錯誤の上で洗練されている雰囲気を感じました。

「こんな風にしてみたら速くなるかもね、知らんけど」みたいなことを無限に話していたような気がします。

ここでやろうとしていることは「コンピュータを数学に活かす」ということであり、私が仕事でやろうとしている「数学をコンピュータに活かす」とは真逆の考え方です。しかし、真逆にした方が色々としっくりきました。⁵
なんというか、物事があまり腑に落ちないときは、考え方を逆にしたら良いのですね。

素数探索プログラムの中身

素数探索プログラムの中身を少し見てみます。
今回は、指定された手札を全て使って作れる最大素数を探索するmax_prime関数に注目します。
関数の使い方や概要はドキュメントとして整備してくれています(えらすぎる)。

max_prime関数

bigint max_prime(hand h)

この関数は、手札 h をすべて使って作ることができる素数のうち最大のものを返します。
例えば、手札1234QKを使って作れる最大素数が知りたければ、

std::cout << max_prime(hand("1234QK")) << std::endl;

このようなコードを実行します。すると関数の中身が実行され、

43211213

と表示されて、43211213が最大素数だとわかります。

素数探索プログラムの高速化ってどうやるの？？

ぼっちざろっく第8話で、もうすぐ夏休みが終わることを受け入れられないぼっちちゃんに、虹夏ちゃんがこんな言葉をかけます。

ぼっちちゃん、現実を見て！

プログラムの高速化も同じことです。ネットでプログラムを速くする方法を調べると、

• 並列化
• コンパイルオプション
• ベクトル化
• GPU
• キャッシュメモリ

など色々と情報が出てきます。しかし、これらを語る前に「現実を見ていない」のだとしたら、それは全て机上の空論で何の意味もありません。

プログラムを高速化したい時、まず一番初めに必ずやるべきことがあります。それは勉強でも作戦会議でもなく、

• 今のありのままのプログラムを実行して、どこに時間がかかっているかを特定する

つまり「現実を見る」ことです。

往々にして、数値計算や高速化の話に銀の弾丸はありません。1つ1つの事例に対して、どこに問題があって、なぜ問題になっていて、どのように解決するかを考えます。この辺が数値計算の泥臭くも面白い所です。

というわけで、素数探索プログラムを実行し、時間がかかっている箇所を特定してみましょう。ちなみにこの作業をプロファイリングなどと言います。

ところで22Kは「虹夏素数」として私は覚えています。

プロファイリング

今回は、上で紹介したmax_prime関数を実行し、それにかかる時間を測定してみます。⁶
ただし、関数の実行時間にはバラつきがあるので関数を1回実行しただけでは不十分です。また、ここでは手札の枚数が多い場合の最大素数に興味があります。そこで、下記の手順で時間を測ることにします。

1. 80枚の手札をランダムに生成する
2. その手札に対しmax_prime関数を実行する
3. 1~2を32回繰り返して時間を測定し、1回あたりにかかった平均時間を算出する
4. 1~3までを試行と呼ぶ。この試行を8回繰り返す

この手順を実行して、結果をグラフにしたものが下記です。

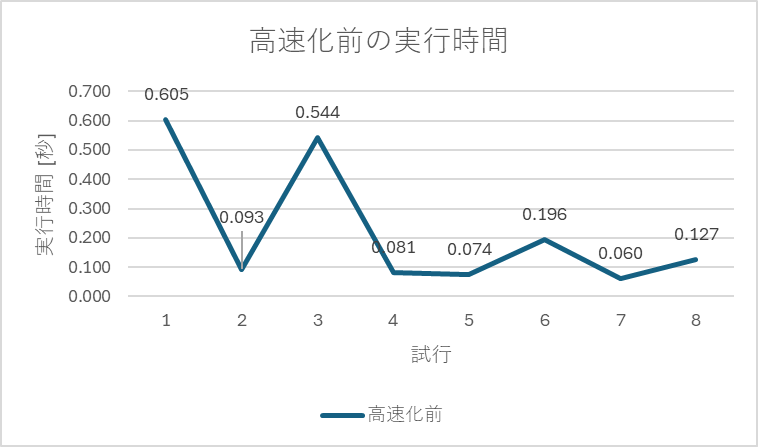
要するに、max_prime関数1回あたりの平均時間はだいたい0.06~0.6秒くらいであるということです。

ここでは踏み入りませんが、プロファイリング用のツール⁷を使うことで、どの処理にどれくらい時間がかかっているかを細かく見ることもできます。今回のケースは、どうやら指数関数(pow)に時間がかかっていそうですね。

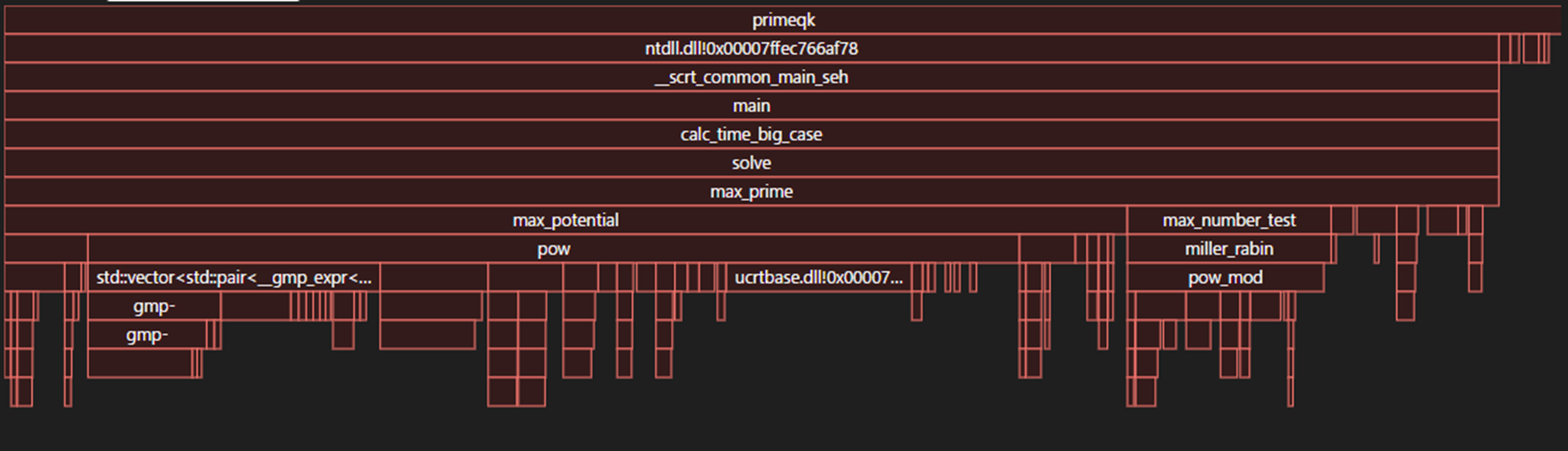
これでいったん、現状の素数探索にかかっている時間がわかりました。
それではいよいよ、素数探索を高速化していきましょう。

🌻刺身にたんぽぽを乗せる仕事について考える

あなたは今、刺身製造工場で働いています。あなたが任されている仕事は以下の3つです。

1. パックに刺身を乗せる
2. 刺身にたんぽぽを乗せる
3. パックの蓋を被せる

この3つの仕事を高速化するにはどうすればよいでしょうか？

......

ここで重要なのは、1,2,3を同時に行うことはできないということです。
なぜなら、刺身を用意しないとたんぽぽを乗せられず、たんぽぽを乗せないとパックの蓋をかぶせられないからです。
つまり、仕事は必ず1→2→3の順に行わなければなりません。

......

ですが、1同士,2同士,3同士は並行して作業することができます。
つまり左右両手を使い、片手ずつ刺身を乗せ、片手ずつたんぽぽを乗せ、片手ずつ蓋をかぶせればよいのです。これで効率は2倍になります。

プログラムも同じです。処理の中には、同時に処理できる部分と、どうしても同時には処理できない部分があります。そして、同時に処理できる部分は、スレッド並列化という手法により並列処理ができます。

説明は省略しますが、先ほどのプロファイリングで時間がかかると判明した処理は、幸運にも並列処理ができそうです。
今回は、スレッド並列化でよく使われるOpenMPをmax_prime関数に導入してみました。⁸

コードの99%は省略しますが、一番重要なのは以下の1行です。

omp_set_num_threads(16);

これはつまり、16個のたんぽぽを同時に刺身に乗せよという命令です。ここまで真面目に読んでいただいた方なら、これが持つ意味を理解できるはずです。

高速化して何倍になったか

読むのが面倒でここまでスクロールしてきた方のために、上で説明したことをわかりやすく簡潔にまとめます。

• 素数探索とは刺身にたんぽぽを乗せる仕事である
• たんぽぽを乗せる仕事を速くするには自分の手を16本に増やせばよい

さて、この作戦により素数探索のmax_prime関数は何倍に高速化されたでしょうか？結果は以下のグラフになります。

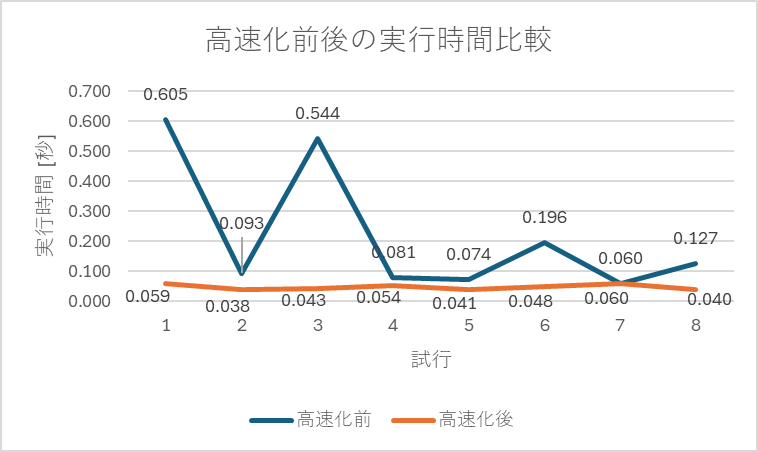
max_prime関数1回あたりの平均時間は、高速化前が0.06~0.6秒くらいだったのが、高速化後は0.04~0.06秒くらいになりました。
バラつきはありますが、1.5倍から10倍くらい速くなったと言えますね！

おまけ

max_prime関数を使うと、80枚の手札(input)で出せる最大素数(output)が計算できます。下記に例をいくつか書いておきます。が、大きすぎてよくわかりません。

input:    Q74179T421281211JJTKJTQJ29JJ1649K121Q267T94J22456197853191TT5182844555457Q676658
output:   999999888887777776666665555555544444444322222222213131212121211111111111111111111110101101101101011

input:    61J3539J529J7T3JJ2874J7JQ9T6QQTT6465QT5899TT472K54TJQQ7TJQK7T93JTK399TJ974K488T6
output:   9999999998888777777766666555554444443333322213131313121212121212121111111111111111111101010101011101010101010101011

input:    33355Q8945522K2361893K2973Q523Q2T83T5499Q7J4931T2T34KJ975K52T1711J4TK993QT779Q24
output:   0

最後に

ここまで読んでいただきありがとうございました。
プログラミングに少し興味を持っていただけたでしょうか？

念のため言っておきますが、この記事で紹介した素数探索プログラムは はち の成果であり、高速化したからと言って私の貢献は1%にも満たないので、勘違いはしないでくださいね。

P.S.
はちへ。作ったコードを共有したいので、もしこれを読んでいたら今度Gitリポジトリへの書き込み権限をください。

明日の記事は、はなぶさんによる「なんかかきます」です。
あまりにも具体性が無くてとても楽しみです！

1. 適当に専門分野のキーワードを挙げると、ソリトン・パンルヴェ・可積分系・非線形微分方程式・離散・超離散・セルオートマトン・箱玉系、など。 ↩

2. 数学徒というものは、好きな命題や式を6つ挙げれば素性が分かります。私は・ガウスの発散定理・コーシーの積分定理・ラグランジュ未定定数法・バナッハの不動点定理・ゲーデルの不完全性定理・選択公理、の6つです。ポケモントレーナーの手持ちポケモンを見れば素性が分かるのと一緒です。 ↩

3. もう少し正確に言うと、CAE(Computer Aided Engineering)に関するソフトウェア開発をしています。 ↩

4. 真面目に言うと、例えば論文を理解する時に数理の強さが活きることがあります。あとは(ちょっとふわっとしていますが)物事を抽象化して理解することは数学出身者の圧倒的な強みだと実感します。逆に具体的な数字や細かい個別事情とかを記憶するのは苦手です。私だけかもですが。 ↩

5. 「数学をコンピュータに活かす」のは言わば「そろばんを高性能にする」ことです。理学・工学問わず沢山の研究者が数十年の時間をかけて日進月歩で進めている領域であり、何ならコンピュータなんて存在しないガウスの時代から高速フーリエ変換(FFT)が発見されている程です(ガウスが意味不明化け物というのもありますが)。
   一方で、逆にした「コンピュータを数学に活かす」のは「問題を解くためにそろばんを使う」ことです。四色定理が有名な事例でしょうか。
   「そろばんを高性能にする」のと「そろばんを使う」のとでは、後者の方がとっつきやすそうですし、ぶわっと色々な想像ができて、可能性も感じますね。 ↩

6. 問題の条件：Joker無し、miller_rabin関数ではk=50
   CPU：AMD Ryzen 9 7950X3D、16コア32スレッド
   メモリ：DDR5-4800 MT/秒、2スロット使用 ↩

7. ここではVisual Studioのパフォーマンスプロファイラーを利用。 ↩

8. スレッドプールという手法を利用。 ↩