#まえがき
前回までの回帰分析の記事を読んでいる前提で説明します。
ここまで扱った数式は以下のような線形回帰のモデルでした。
\tilde{y} = w_0 + w_1 x _1 + \cdots +w_dx_d + \varepsilon
今回は以下のような多項式回帰をモデルとしたアルゴリズムを見てみましょう。
\tilde y = w_0 + w_1 x ^1 + \cdots +w_dx^d + \varepsilon
最小化したい関数は以下のようになります。
E(w) = ||\tilde y(x, w) - y||^2
線形回帰モデルを流用しよう
多項式回帰は線形回帰で書いた内容から置き換えるだけで以下の式を書くことができます。
\mathbf{\hat{y}}
= \left(
\begin{array}{ccc}
w_0 + w_1x_{1}^1 + \cdots + w_dx_{1}^d \\
w_0 + w_1x_{2}^1 + \cdots + w_dx_{2}^d \\
\cdots \\
w_0 + w_1x_{n}^1 + \cdots + w_dx_{n}^d
\end{array}
\right)
= \mathbf{\tilde{M}}\mathbf{w}\tag{6}
ここで
\mathbf{\tilde{M}}= \left(
\begin{array}{ccc}
1 & x_{1}^1 & \cdots & x_{1}^d \\
1 & x_{2}^1 & \cdots & x_{2}^d \\
\cdots \\
1 & x_{n}^1 & \cdots & x_{n}^d
\end{array}
\right) \tag{7}
です。
あとはなんだかんだすれば
(\mathbf{\tilde{M}}^T\mathbf{\tilde{M}}) \mathbf{w} = \mathbf{\tilde{M}}^T\mathbf{y} \tag{8}
でwを求められます。
wが求まればあとはyを求めることができるようになるわけです。
実装してみよう
Pythonで実装してみましょう。
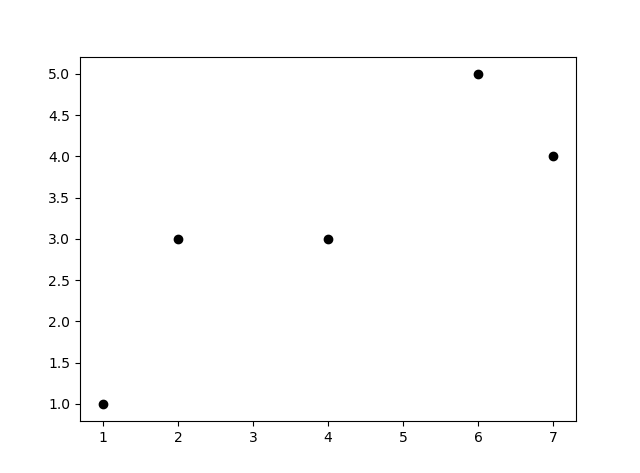
以前と同じデータを使ってみます。
import matplotlib.pyplot as plt
x = [1,2,4,6,7]
y = [1,3,3,5,4]
plt.scatter(x, y)
plt.show()
このデータのwを計算してみます。
import numpy as np
from scipy import linalg
x_pow = []
xx = x.reshape(len(x), 1)
for i in range(1, 10):
x_pow.append(xx**i)
mat = np.concatenate(x_pow, axis=1)
Xtil = np.c_[np.ones(mat.shape[0]), mat] # 式(7)を作った。
A = np.dot(Xtil.T, Xtil)
b = np.dot(Xtil.T, y)
w = linalg.solve(A, b) # 式(8)によってwを計算した。
あとはこれで計算してみるだけです。
def predict(x): # wを利用してyを計算する関数。
r = 0
for i in range(10):
r += x ** i * w[i]
return r
xx = np.linspace(x.min(), x.max(), 300)
yy = np.array([predict(u) for u in xx])
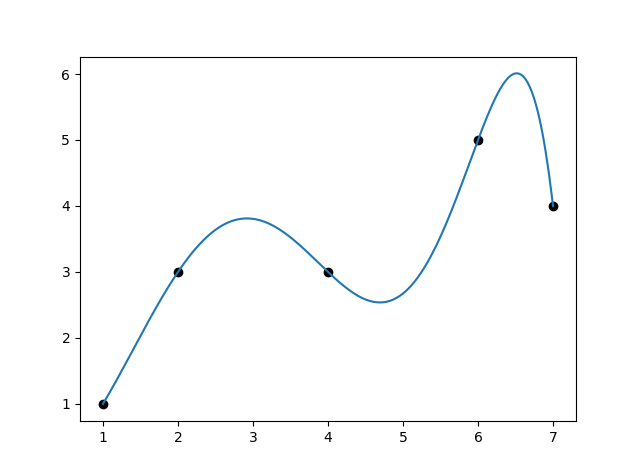
plt.plot(xx, yy)
plt.show()
ぴったり散布図に沿った線が引けました。
これでいいのか？
線形回帰と多項式回帰、それぞれで求めたグラフを比較してみましょう。
左が$y = ax + b$型の線形回帰、右が$y = w + x + x^2 + ...+ x^d$型の多項式回帰です。
ぴったり線に乗っているのは右図ですが、近似するグラフとして採用したいのは左図ですね。
機械学習の目的はぴったり表せるグラフを求めることではなく、未知の値を予想することです。この「未知のデータを予測する能力」のことを汎化性能といいます。この性能が下がるほどぴったり学習してしまうことを、「過学習」といいます。
# 過学習への対策
どうすれば過学習を防げるか。[前回](https://qiita.com/NNNiNiNNN/items/e0d878bd52baddea4569#_reference-82e83f2298fa6c958921)行ったリッジ回帰がその答えの一つです。
リッジ回帰は以下のような式で計算を行います。
E(\mathbf{w}) = ||\mathbf{y} - \mathbf{\tilde{X}\mathbf{w}}||^2 + \lambda ||w || ^2
また、ラッソ回帰というものもあります。
E(\mathbf{w}) = ||\mathbf{y} - \mathbf{\tilde{X}\mathbf{w}}||^2 + \lambda ||w ||_1
どちらも、二乗誤差に重みを変数とした関数を加えたものです。正則化項といいます。リッジ回帰ならその二乗の合計。ラッソ回帰なら1乗の合計。
要するに、重みが複雑になるほどペナルティが入る。そのペナルティを回避しつつ誤差最小を目指すことで、汎化性能を上げることができます。
まとめ
関数を複雑にすればするほど学習時は正確なグラフを作ることができるが、その正確さは予測値の正確さとは別ものである。予測値の正確さを汎化性能、学習しすぎでそれを失った状態を過学習と呼ぶ。
それを回避するための方法にペナルティを加えるという手段がある。リッジ回帰やラッソ回帰がその例である。
「機械学習のエッセンス」という本を参考にしました。この本についてまとめていきます。
前回:リッジ回帰
https://qiita.com/NNNiNiNNN/items/e0d878bd52baddea4569#_reference-82e83f2298fa6c958921
次回:ラッソ回帰
https://qiita.com/NNNiNiNNN/items/75b263298e6a112d5929