Pythonで最小二乗法をしてみよう

#まえがき
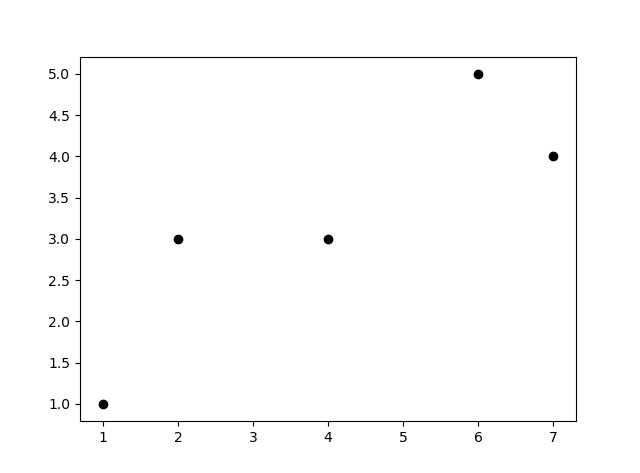
こんな散布図を考えてみましょう。

以下のように作ります。

import matplotlib.pyplot as plt

x = [1,2,4,6,7]
y = [1,3,3,5,4]

plt.scatter(x, y)
plt.show()

この散布図を近似する表現する直線が欲しい。こういうの↓。

これを最小二乗法を使って求めてみましょう。

y = ax型関数への近似

目的の直線を

y = ax

型の関数と仮定します。
この関数では$x$地点でのy座標は$ax$になります。実際のy座標との誤差は

ax- y

ですね。
統計学では誤差はだいたい二乗して扱います。

(ax - y)^2

これを全要素足し合わせると

E = \sum ^n _ {i = 1}(ax_i - y)^2

こうですね。これを最小化できるようにaを調整すればいいわけです。
そのためにaで微分してみましょう。

 \frac{\partial E}{\partial a} = 0
 

となれば最小値をとるわけです。

 \frac{\partial E}{\partial a} = \sum 2x_i (ax _i - y_i)\\
= 2(a\sum x_i^2 - \sum x_iy_i)
 

これが=0の時最小値なので、aについて整理して

a = {\sum x_i y_i \over \sum x_i^2}  = {\mathbf{x}^T \mathbf{y} \over ||\mathbf{x}||^2}

これを計算すればEが最小となるaが求まります。
#実装してみよう
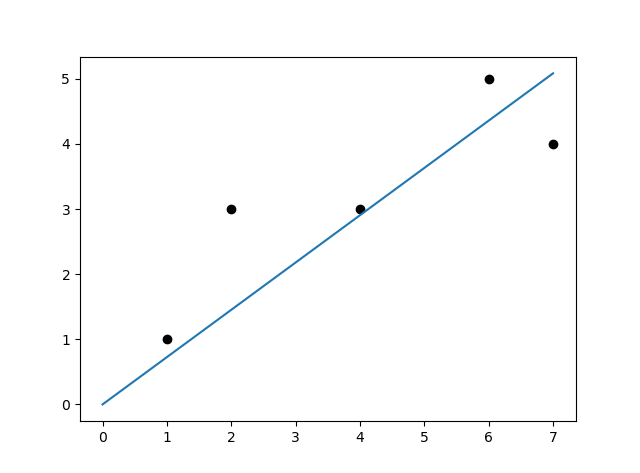
Pythonに実装すると以下のようになります。

import numpy as np #np.dot(x, y) xyの内積をとる関数。
import matplotlib.pyplot as plt

x = np.array([1,2,4,6,7]) # 内積計算のためにnp.arrayで作る。
y = np.array([1,3,3,5,4])

def reg1dim(x, y):
    a = np.dot(x, y)/ (x ** 2).sum()
    return a

a = reg1dim(x, y)

plt.scatter(x, y, color="k")
plt.plot([0,x.max()], [0, a * x.max()]) # x.max() 配列xの最大値まで 
plt.show()

できたグラフがこちら。

いい感じの直線が引けました。
#y = ax + b型関数への近似
先ほど求めた関数では、原点を通る直線しか引けません。
今度は

y = ax + b

型の直線を求めてみましょう。
先ほどと同様に考えて、最小化したい値は

E = \sum ^n _ {i = 1}(ax_i +b - y)^2

これをaとbについての関数だと考えて、aとbそれぞれで偏微分します。

 \frac{\partial E}{\partial a} = 0 \\
 \frac{\partial E}{\partial b} = 0
 

になればいいわけです。

 \frac{\partial E}{\partial a} = \sum ^n_{i= 1} 2x_i (ax _i+ b - y_i) = 0 \tag{1}
 

また

 \frac{\partial E}{\partial b} = \sum ^n_{i= 1}(ax _i+ b - y_i) = 0

これをbについて整理して

b ={ 1\over n}\sum^n_{i= 1}(y_i - ax_i)　\tag{2}
 

(1)式に(2)式を代入してaについて整理すれば以下の値を得ます。

a = {\sum ^n _ {i = 1}x_i y_i - {1 \over n}\sum^n_{i = 1}x_i \sum^n_{i = 1}y_i \over \sum^n_{i = 1}x_i^2 - {1 \over n}(\sum^n_{i = 1}x_i)^2} \tag{3}

式変形の手順は省略。読者への演習問題とする。
#実装してみよう
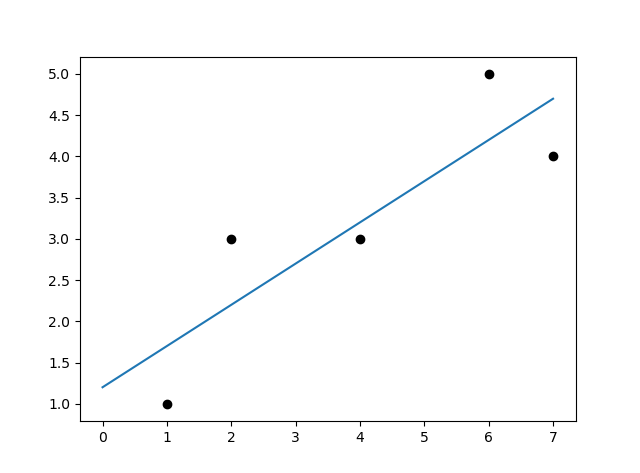
以上の式をpythonに入力すると以下のようになります。

import numpy as np
import matplotlib.pyplot as plt

x = np.array([1,2,4,6,7])
y = np.array([1,3,3,5,4])

def reg1dim(x, y):
    n = len(x)
    a = ((np.dot(x, y)- y.sum() * x.sum()/n)/
        ((x ** 2).sum() - x.sum()**2 / n))
    b = (y.sum() - a * x.sum())/n
    return a, b

a, b = reg1dim(x, y)

plt.scatter(x, y, color="k")
plt.plot([0, x.max()], [b, a * x.max() + b]) #(0, b)地点から(xの最大値,ax + b)地点までの線
plt.show()

こんな感じ。さっきよりそれっぽいですね。

#　特徴量ベクトルの多次元化
ここまで特徴量ベクトル($\mathbf{x}$)が1次元である場合の直線近似を見ました。
次に多次元における最小二乗法を見てみましょう。
求めるモデルの一般式は以下のようなものです。

y = w_0 + w_1x_1 + w_2x_2 + \cdots + w_dx_d + \varepsilon \tag{4}

ここで$x_0, \cdots ,x_d$は入力変数、 $w_0, w_1, \cdots , w_d$はパラメータ、yはターゲットを示す。εはノイズ。
(4)式はベクトル表記を用いて以下のように表せます。

y = \mathbf{w}^T \mathbf{ \tilde{x}} \tag{5}

ここで$\mathbf{\tilde{x}} = (1, x_1, x_2, \cdots, x_d)^T$、$\mathbf{w} = (w_0, w_1, \cdots, w_d)^T$です。
さらに複数のパラメータyをベクトルとして扱うと、以下のように表すことができます。

\mathbf{\hat{y}} (\mathbf{w}) =
\left(
    \begin{array}{ccc}
      \mathbf{w}^T \mathbf{ \tilde{x}}_1 \\
      \mathbf{w}^T \mathbf{ \tilde{x}}_2 \\
      \cdots \\
\mathbf{w}^T \mathbf{ \tilde{x}}_n
    \end{array}
  \right)
= \left(
    \begin{array}{ccc}
      w_0 + w_1x_{11} + \cdots + w_dx_{1d} \\
      w_0 + w_1x_{21} + \cdots + w_dx_{2d} \\
      \cdots \\
w_0 + w_1x_{n1} + \cdots + w_dx_{nd}
    \end{array}
  \right)
= \mathbf{\tilde{X}}\mathbf{w}\tag{6}

ここで

\mathbf{\tilde{X}}= \left(
    \begin{array}{ccc}
      1 & x_{11} & \cdots & x_{1d} \\
      1 & x_{21} & \cdots & x_{2d} \\
      \cdots \\
1 & x_{n1} & \cdots & x_{nd}
    \end{array}
  \right) \tag{7}

です。
1次元の場合と同様に、(6)式から最小化したい誤差は以下の式で表されます。

E(\mathbf{w}) = ||\mathbf{y} - \mathbf{\tilde{X}\mathbf{w}}||^2\\
= \mathbf{y}^T\mathbf{y}-\mathbf{w}\mathbf{\tilde{X}}^T\mathbf{y} - \mathbf{y}^T\mathbf{\tilde{X}w} + \mathbf{w}^T \mathbf{\tilde{X}}^T \mathbf{\tilde{X}}\mathbf{w}

あとはこれを$\mathbf{w}$で微分して

\Delta E(\mathbf{w})= -2 \mathbf{\tilde{X}}^T \mathbf{y} + 2 \mathbf{\tilde{X}}^T \mathbf{\tilde{X}}\mathbf{w}

これを=0として整理すれば

\mathbf{w} = (\mathbf{\tilde{X}}^T\mathbf{\tilde{X}})^{-1}\mathbf{\tilde{X}}^T\mathbf{y}

こうしてEを最小化するwが求まりました。
これを解くwを求めるために標準形にしておきましょう。

(\mathbf{\tilde{X}}^T\mathbf{\tilde{X}}) \mathbf{w} = \mathbf{\tilde{X}}^T\mathbf{y} \tag{8}

これで$Ax = b$を標準形とする関数で解くことができます。
#実装してみよう
xを二次元データにして、yと合わせて3次元の分析をしましょう。
まず訓練用データを作ります。

import numpy as np

# y = w[0] + w[1]x[1] + w[2]x[2]型。
#今回はw = [1, 2, 3]とする。
X = np.random.random((100, 2)) * 10 # 0から1*10の範囲をとる100*2の行列
y = 1 + 2 * X[:, 0] + 3 * X[:, 1] + np.random.randn(100)
#x0とx1の座標からyを作成。randnで本来の値にノイズを加えている。

この散布図を出力したものが以下の図です。

それでは最小二乗法を行ってみましょう。以下を付け足します。

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d # 3D表示に使う
from scipy import linalg # linalg.solve(A, b) 　Ax = bの解を求める関数

Xtil = np.c_[np.ones(X.shape[0]), X] # Xの行列の左端に[1,1,1,...,1]^Tを加える。(7)式を確認しよう
A = np.dot(Xtil.T, Xtil) # 標準形A,bに当てはめる。
b = np.dot(Xtil.T, y)
w = linalg.solve(A, b) # (8)式をwについて解く。

xmesh, ymesh = np.meshgrid(np.linspace(0, 10, 20),
                            np.linspace(0, 10, 20))
zmesh = (w[0] + w[1] * xmesh.ravel() +
        w[2] * ymesh.ravel()).reshape(xmesh.shape)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], y, color='k')
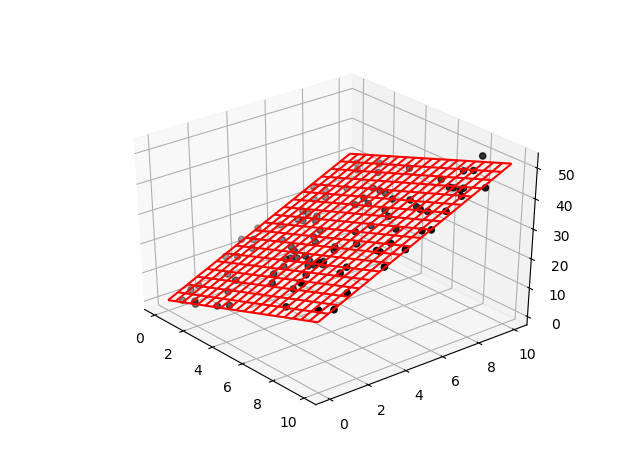
ax.plot_wireframe(xmesh, ymesh, zmesh, color='r')
plt.show()

wの値をprintしてみると

係数: [0.76815141 2.05360787 2.99541161]

と出ました。
元がw = [1,2,3]のはずなので、まあまあといったところでしょうか。

まとめ

数学を手計算でガリガリ解いてそのまま入力することで最小二乗法を行うことができました。

『機械学習のエッセンス』という本を参考にしました。この本についてまとめていきます。次回も統計手法を見てみましょう。
前回:数理最適化問題
https://qiita.com/NNNiNiNNN/items/57e409e5dbcfac9897ec
次回:リッジ回帰
https://qiita.com/NNNiNiNNN/items/e0d878bd52baddea4569