フーリエ変換の(雑な)導出とライブラリなしの実装を行い、フーリエ変換に対する理解を深めたいと思います。
まえがき
関数は、それを構成する関数の組み合わせで表現することができます。例えば関数$F(x)$の基底が関数f, g, hであるならば
$$ F(x) = af+ bg+ ch $$
となるa, b, cの組み合わせ(ただし0以外)が存在します。
では、任意の関数を以下のような組み合わせで表すことを考えてみましょう。ただし、関数の範囲は今回$0< x < 2\pi$とします。
$$ f( x ) = a_0 \times{1\over 2} + (a_1 \times \cos x + a_2 \times \cos2 x + ... + a_\infty\cos\infty)\ + (b_1 \times \sin x + b_2 \times \sin2 x + ... + b_\infty\sin\infty) $$
1/2と、三角関数という無限の成分を組み合わせて関数を表現してみます。整理して書くと以下のようになります。
$$f ( x) = {a_0 \over 2} + \sum ^ \infty _ {k = 1}(a_k \cos k x + b_k \sin k x) \tag{1}$$
ここで使われている$a_0, a_n, b_k$を導出してみましょう。
必要な積分知識
導出の前に積分の知識を確認しましょう。積分が苦手な人は紙とノートで計算してみてください。
まずはこの二つ。
$$ \int^{2\pi} _ 0 \cos n x dx = 0 \tag{2}$$
$$ \int^{2\pi} _ 0 \sin n x dx = 0 \tag{3}$$
さらにこれを使って以下の五つの積分を確認。(4), (6)式は$n\neq m$とします。
$$ \int^{2\pi} _ 0 \cos n x \cos m x dx= {1\over 2} \int ^{2\pi} _ 0 (\cos (n + m)x + \cos (n - m)x)dx = 0 \tag{4}$$
$$ \int ^{2\pi} _ 0 \cos^2 nx dx = \int ^{2\pi} _ 0 {1 + \cos2x \over 2}dx = \pi \tag{5}$$
$$ \int^{2\pi} _ 0 \sin n x \sin m x dx = {1\over 2} \int ^{2\pi} _ 0 (\cos (n + m)x - \cos (n - m)x)dx = 0
\tag{6}$$
$$ \int ^{2\pi} _ 0 \sin^2 nx dx = \int ^{2\pi} _ 0 {1 - \cos2x \over 2}dx = \pi \tag{7}$$
$$ \int^{2\pi} _ 0 \sin n x \cos m x dx ={1\over 2} \int ^{2\pi} _ 0 (\sin (n + m)x + \sin (n - m)x)dx = 0 \tag{8} $$
このように、違う要素同士をかけると0になる性質を直交性といいます。
フーリエ級数の導出
$$f ( x) = {a_0 \over 2} + \sum ^ \infty _ {k = 1}(a_k \cos k x + b_k \sin k x) \tag{1}$$
この式の$a_0, a_n, b_n$を導出しましょう。
(1)式の両辺を$0から2\pi$まで積分する。(2),(3)式から三角関数が消えて
$$\int^{2\pi} _ 0 f(x)dx = {a_0\over 2} \int ^{2\pi } _ 0dx $$
$$ \int^{2\pi} _ 0 f(x)dx = {a_0} \pi $$
整理して
$$ a_0 = {1\over \pi}\int^{2\pi} _ 0 f(x)dx \tag{9} $$
今度は(1)式の両辺に$\cos n x$をかけて同様に積分すると、ほとんどの三角関数の成分が消えて
$$\int^{2\pi} _ 0 f(x) \cos n x dx = a_n \pi $$
$$ a_n = {1\over \pi} \int^{2\pi} _ 0 f(x) \cos n x dx \tag{10} $$
同様に両辺に$\sin nx$をかけて積分すると
$$\int^{2\pi} _ 0 f(x) \sin n x dx = b_n \pi $$
$$ b_n = {1\over \pi} \int^{2\pi} _ 0 f(x) \sin n x dx \tag{11} $$
これでフーリエ級数展開の係数を計算できます。
複素数表示に拡張してみよう
オイラーの公式というものがあります。
$$ e^{ix} = \cos x + i \sin x \tag{12} $$
これを利用して$a_n$と$b_n$を$c_n$で表してみましょう。まず
$$ c_ 0 = {a_0 \over 2} $$
$n> 0$の時
$$ c_n = {a_n -ib_n \over 2 }$$
$$ c_{-n} = {a_n + ib_n \over 2 }$$
とおくと、(1)式は
$$ f(x) = \sum ^{\infty}_{-\infty } c_n e^{inx} \tag{13} $$
と表すことができます(わからなかったら適当なnと-nについて$c_n$とオイラーの公式を展開してみよう)。
この$c_n$を$a_n, b_n$と同じように積分して計算すると、
$$ c_n = {1 \over 2\pi } \int ^{2\pi} _ 0 f(x)e^{-inx}dx \tag{14}$$
と求まります。
よく見る形にしましょう
フーリエ変換$F(x)$は要するに求めた級数展開の$c_n$とだいたい同じ概念です。(14)式を参考に以下の式を書けます。係数は外しておきます。
$$ F(t) = \int ^{2\pi} _ {0} f(x)e^{-itx}dx \tag{14} $$
フーリエ変換で求めた式を元の式に戻すには(13)式を参考にしましょう。ただし積分表示にしておきます。
$$ f(x) = {1\over 2\pi} \int ^{\infty } _ {-\infty }F(t)e^{itx}dx \tag{15} $$
これが逆変換です。
離散フーリエ変換にしましょう
積分で表したフーリエ変換の式は以下のように変換することができます。
$$ F(t) = \int ^{2\pi} _ {0} f(x)e^{-itx}dx = \lim _{n \to \infty}{1\over n}\sum ^{n -1} _{k=0} f({2\pi k \over n})e^{- 2\pi i k t \over n} \tag{16}$$
0から2$\pi$までを無限に細かく区切って区分求積の形にしたものです。${2\pi k \over n}$が最大2$\pi$となるxの値を示します。
このnの値が波の"解像度"といえる値で、(16)式では無限となっています。もちろん無限の処理は実装できないので、解像度は落ちますが有限にしましょう。係数は消します。
$$ F(t) = \sum ^{n -1} _{k=0} f({2\pi k \over n})e^{-2\pi i k t \over n} \tag{17}$$
これが離散フーリエ変換です。
実装してみよう
まず波を作成します。
import numpy as np
import cmath
import matplotlib.pyplot as plt
x = np.arange(0, 2 * cmath.pi, 0.1)
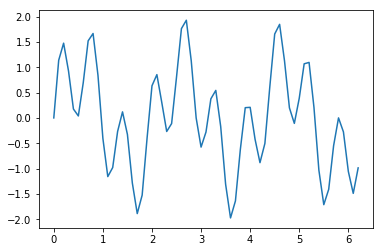
y = np.sin(3 * x) + np.sin(10 * x)
plt.plot(x, y)
周期3の波と周期10の波が含まれています。
離散フーリエ変換dft()を実装します。ほとんど(17)式のままです。
$$ F(t) = \sum ^{n -1} _{k=0} f({2\pi k \over n})e^{-2\pi i k t \over n} \tag{17}$$
def dft(f):
n = len(f)
Y = []
N = 20 # 解像度
for t in range(N):
y = 0j
for x in range(n):
a = 2 * cmath.pi * t * x / n
y += f[x] * cmath.e**(-1j * a)
Y.append(y)
return Y
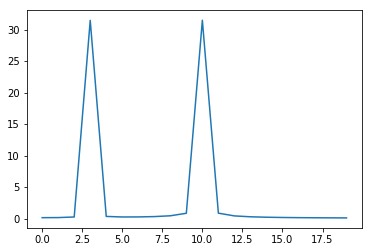
plt.plot(np.abs(dft(y))) # 絶対値を出力
$t = 3, 10$にピークが確認できます。元のyには3, 10の周期の波を入れたのでまさにその通りの結果がでています。なお、これ以上深く計算すると鏡像という左右対称になるピークが出てきます。それについては余白が足りないので今回は触れません。
離散フーリエ変換の実装ができました。
参考にしたもの
記数式に関しては主にhttps://qiita.com/GCLemon/items/8fd3f29a8ec8cdaf675a
実装に関しては主にhttps://qiita.com/sai-sui/items/814117940c1d1b2b1785
を参考にしました。(こちらの方がpythonらしい綺麗な書き方をしています)
一部数式は書籍『数理科学の方法』(財団法人 放送大学教育振興会)
を参考にしました。