はじめに
自己紹介
この度 Amusement Creators Advent Calendar に参加させていただいた、檸檬茶(レモンティー)と申します。最近はよくシェーダーを書いてます。1ヶ月ほど前、フーリエ変換をしてくれるだけのクソライブラリを作って Altseed と NAudio 使ってオーディオビジュアライザを作ってました。今回はこの「フーリエ変換」の部分を実装していきます。
この記事の概要
この記事では「自力で」フーリエ変換を実装する方法をご紹介いたします。フーリエ変換を「自力で」実装するので、Math.Netに搭載されている高速フーリエ変換や、NAudioに搭載されている周波数解析機能などは一切使いません。もちろん、UnityなどのゲームエンジンやOpenSiv3Dなどのメディアアート用のライブラリも一切使わず、純粋に「自力で」フーリエ変換を実装することを目指しています。
注意事項
- この記事では数学系の話を延々とします。
- この記事におけるソースコードは、すべてC#によって記述されています。
フーリエ変換
フーリエ変換とは
フーリエ変換は以下のような式で表すことができます。
$$\mathcal{F}(\omega)=\int_{0}^{2\pi} f(t)e^{-it\omega}dt$$
......と一口に言われて理解できる人なんてまずいないと思います。
フーリエ変換のコンセプトを一言で言い表すと、
「波形の情報からどの周波数の波がどのくらいの大きさで含まれているのかを導出する」
って感じです。
このコンセプトを理解していただくために、フーリエ級数を導出してみます。
まず、遍く全ての波は正弦関数($\sin$とか$\cos$とか)で表すことができるとします。すなわち、波形を表す関数を
$$f(\theta) = C+\sum_{k=1}^{\infty}a_k\cos(k\theta) +b_k\sin(k\theta)$$
とします。ただし$C$は定数であるとします。高校生以上の方々にはぜひ実際に計算してみて欲しいのですが、実はのこ関数 $f(\theta)$、$\sin$や$\cos$を掛けて積分すると......
$$\int_{0}^{2\pi}f(\theta)\cos(k\theta)d\theta = \pi a_k,\ \ \ \ \ \ \ \int_{0}^{2\pi}f(\theta)\sin(k\theta)d\theta = \pi b_k$$
$$a_k = \frac{1}{\pi}\int_{0}^{2\pi}f(\theta)\cos(k\theta)d\theta,\ \ \ \ \ \ \ b_k = \frac{1}{\pi}\int_{0}^{2\pi}f(\theta)\sin(k\theta)d\theta$$
となることがわかります。また$k=0$を代入すると、
$$a_0 = \frac{1}{\pi}\int_{0}^{2\pi}f(\theta)\cos(0)d\theta = \frac{1}{\pi}\int_{0}^{2\pi}f(\theta)d\theta=2C$$$$b_0 = \frac{1}{\pi}\int_{0}^{2\pi}f(\theta)\sin(0)d\theta = \frac{1}{\pi}\int_{0}^{2\pi}0d\theta=0$$
となり、$C=\frac{a_0}{2}$であることがわかります。以上をまとめるとこのようにして数式に表すことができます。
$$f(\theta) = \frac{a_0}{2} + \sum_{k=1}^{\infty}a_k\cos(k\theta) +b_k\sin(k\theta)$$
$$a_k = \frac{1}{\pi}\int_{0}^{2\pi}f(\theta)\cos(k\theta)d\theta,\ \ \ \ \ \ \ b_k = \frac{1}{\pi}\int_{0}^{2\pi}f(\theta)\sin(k\theta)d\theta$$
これがフーリエ級数です。この級数において、$a_k$および$b_k$はそれぞれ$\cos$と$\sin$の係数、すなわち波形の振幅を表しています。つまり、この級数を用いることで波の振幅をあらかた求めることができます!!
ここからオイラーの公式を適用して級数を積分の形に変形し、積分範囲を無限大に拡張すると、
$$\mathcal{F}(\omega)=\int_{0}^{2\pi} f(t)e^{-it\omega}dt$$
といったような数式が出来上がります。モノホンのフーリエ変換の導出過程を書き連ねると記事がとんでもなく長くなってしまうため、興味のある方は「高校数学でわかるフーリエ変換(竹内淳 様 / 講談社 ブルーバックス)」をご参照ください。
※フーリエ変換の積分範囲がなぜ $0$ から $2\pi$ なのかは次節で分かります。
ちなみに逆変換も載せておきます。
$$f(t)=\frac{1}{2\pi}\int_{-\infty}^\infty \mathcal{F}(\omega)e^{it\omega}d\omega$$
離散フーリエ変換
さて、フーリエ変換を紹介したのは良いのですが、いざフーリエ変換を計算機(つまりパソコン)にやらせようとすると、計算機は数学でやるような積分計算を完璧に行うことはできません。これを計算機にもできるようにするには、導出したフーリエ変換を級数形式に戻してやる必要があります。といっても、先ほど説明したフーリエ級数に逆戻りするわけではありません。
では、まずフーリエ変換を区分求積の形にしてやります。
$$\mathcal{F}(\omega)=\int_0^{2\pi} f(t)e^{-it\omega}dt=\lim_{n\rightarrow\infty}\frac{1}{n}\sum_{k=0}^{n-1}f\left(\frac{2\pi k}{n}\right)e^\frac{2\pi ik\omega}{n}$$
また積分形式のフーリエ変換において、$f(t)$は数学的な関数として無限大のデータを持っています。しかしながら、計算機は有限個のデータしか扱うことができません。そこで $n$ を有限の値とすると、
$$\mathcal{F}(\omega)=\frac{1}{n}\sum_{k=0}^{n-1}f\left(\frac{2\pi k}{n}\right)e^\frac{2\pi ik\omega}{n}$$
となります。この式において、$\frac{2\pi k}{n}$は離散的な値を取り、かつ$f\left(\frac{2\pi k}{n}\right)$が持つデータの数は有限個となります。この形式のフーリエ変換であれば、計算機でも扱いやすくなります。これが離散フーリエ変換です。少し拡張(?)して、$n$ 個の振幅のサンプル $f_0,\ f_1,\ ...,\ f_{n-1}$ を与えてフーリエ変換するとき、式は以下のようになります。
$$\mathcal{F}(\omega)=\sum_{k=0}^{n-1}f_ke^\frac{2\pi ik\omega}{n}$$
ここで、冒頭にて紹介したフーリエ変換において、積分範囲が $0$ から $2\pi$ であるのは、区分求積の形にするのに都合がいいからです。
フーリエ変換を行うプログラムを作るには、この離散フーリエ変換なるものをソースコードに起こすだけです。それも、案外少ないストローク数で記述できます。以下のソースコードは、C#で離散フーリエ変換を実装したものとなります。
using System;
using FourierTransform;
namespace FourierTransform
{
// 愚直に離散フーリエ変換を行うための構造体
public struct DiscreteFourierTransform {
// 波サンプルデータの長さ
int Samples;
// コンストラクタ
public DiscreteFourierTransform(int Samples) {
// 引数の値が2の自然数乗でなければ例外を投げる
for(int i = 2; i <= Samples; i *= 2)
if(Samples % i != 0 || Samples <= 0) throw new DomainException();
// 波サンプルデータの長さを格納
this.Samples = Samples;
}
// 周波数成分を取得するメソッド
// 引数 Function には自作した窓関数を指定することができる
public double[] GetSpectrum(double[] WaveSamples, WindowFunction Window) {
// 引数となる配列の長さが Samples に等しくなければ例外を投げる
if(WaveSamples.Length != Samples) throw new SampleDataLengthException();
// 返り値になる周波数成分データ
double[] Spectrum = new double[Samples];
// 波サンプルに窓関数を掛ける
for(int i = 0; i < Samples; i++) WaveSamples[i] *= Window((double)i / Samples);
// 離散フーリエ変換
for(int i = 0; i < Samples; i++) {
double re = 0, im = 0;
for(int j = 0; j < Samples; j++) {
double arg = -2 * Math.PI / Samples * i * j;
re += Math.Cos(arg) * WaveSamples[j];
im += Math.Sin(arg) * WaveSamples[j];
}
Spectrum[i] = Math.Sqrt(re * re + im * im);
}
// Spectrum を返す
return Spectrum;
}
}
}
NAudio と Altseed とともにこのプログラムを利用して、簡易的なオーディオビジュアライザを作るとこんな感じになります。因みに波のサンプル数は1024個です。
無事にフーリエ変換を実装することができました!!!
......と言いたいところですが、このプログラムでオーディオビジュアライザを作ったとき、1024個といった大きなデータを処理させようとすると馬鹿みたいに重くなります。したがって、大きなデータを扱うオーディオビジュアライザを作るには、より高速でフーリエ変換を行うためのプログラムが必要になります。
高速フーリエ変換
賢く高速にフーリエ変換をするにはかなりコツが必要になります。より詳しい理解に関しては「数値計算法(三井田惇郎 様, 須田宇宙 様 / 森北出版)」をご参照ください。高速フーリエ変換を理解する第一ステップとして、離散フーリエ変換を以下のようにしてやります。
$$\mathcal{F}(\omega)=\sum_{k=0}^{n-1}f_ke^\frac{2\pi ik\omega}{n}=\sum_{k=0}^{\frac{n}{2}-1}f_{2k}e^\frac{2\pi ik\omega}{n/2}+e^\frac{2\pi i\omega}{n}\sum_{k=0}^{\frac{n}{2}-1}f_{2k+1}e^\frac{2\pi ik\omega}{n/2}=\mathcal{F}_E(\omega)+e^\frac{2\pi i\omega}{n}\mathcal{F}_O(\omega)$$
すなわちこの式では、波のサンプルを奇数番目のものと偶数番目のものを分けて、それぞれに離散フーリエ変換を施したあとに、奇数番目の和に「回転因子」なるものを掛けることで、データ全体のフーリエ変換を実現しています。
ここで、こんな式を用意します。
$$\mathcal{F}\left(\omega + \frac{n}{2}\right)=\sum_{k=0}^{\frac{n}{2}-1}f_{2k}e^\frac{2\pi ik\omega}{n/2}-e^\frac{2\pi i\omega}{n}\sum_{k=0}^{\frac{n}{2}-1}f_{2k+1}e^\frac{2\pi ik\omega}{n/2}=\mathcal{F}_E(\omega)-e^\frac{2\pi i\omega}{n}\mathcal{F}_O(\omega)$$
この式があることで、奇数部分と偶数部分のフーリエ変換があれば2つの周波数帯成分を知ることができます。直感的には、
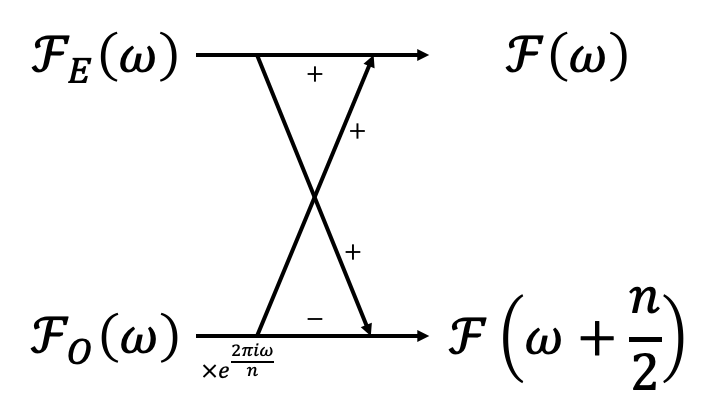
みたいな感じです。奇数部分と偶数部分についてこのような操作を続けていくと、最終的には2つのデータをフーリエ変換するものに行き着くはずです。このとき、データの並び順を見てみると、「ビット反転」と呼ばれ、10進数を2進数に直したものを左右逆に並べて、それをまた10進数に直したものになっています。例えば、0~7のビット反転は以下のようになります。
0 → 000 → 000 → 0
1 → 001 → 100 → 4
2 → 010 → 010 → 2
3 → 011 → 110 → 6
4 → 100 → 001 → 1
5 → 101 → 101 → 5
6 → 110 → 011 → 3
7 → 111 → 111 → 7
以上をまとめると、高速フーリエ変換の原理を直感的に表現すると下図のようになります。
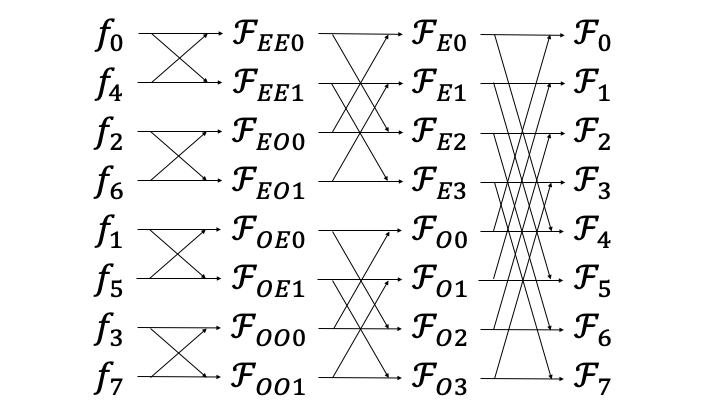
このような演算は「バタフライ演算」と呼ばれています。バタフライ演算を用いることで、従来の離散フーリエ変換に比べて大きなデータをより素早く計算することができます。1024個のデータであれば、計算時間が200分の1になるそうです。では、このバタフライ演算に基づいた高速フーリエ変換なるものを、C#で実装していきます。
using System;
using FourierTransform;
namespace FourierTransform {
// 高速で離散フーリエ変換を行うための構造体
public struct FastFourierTransform {
// 波サンプルデータの長さ
int Samples;
// 回転因子
double[,] Twiddle;
// ビット逆順
int[] Bitreverse;
// コンストラクタ
public FastFourierTransform(int Samples) {
// 引数の値が2の自然数乗でなければ例外を投げる
for(int i = 2; i <= Samples; i *= 2)
if(Samples % i != 0 || Samples <= 0) throw new DomainException();
// 波サンプルデータの長さを格納
this.Samples = Samples;
// 回転因子を格納する
Twiddle = new double[2, Samples / 2];
for(int i = 0; i < Samples / 2; i++) {
double arg = -2.0 * Math.PI / Samples * i;
Twiddle[0, i] = Math.Cos(arg);
Twiddle[1, i] = Math.Sin(arg);
}
// ビット逆順を格納する
Bitreverse = new int[Samples];
for(int i = 0; i < Samples; i++) {
int Order = i, Reverse = 0;
for(int j = Samples / 2; j >= 1; j /= 2) {
Reverse += (Order % 2) * j;
Order /= 2;
}
Bitreverse[i] = Reverse;
}
}
// 周波数成分を取得するメソッド
// 引数 Function には自作した窓関数を指定することができる
public double[] GetSpectrum(double[] WaveSamples, WindowFunction Window) {
// 引数となる配列の長さが Samples に等しくなければ例外を投げる
if(WaveSamples.Length != Samples) throw new SampleDataLengthException();
// 引数の波形データは予め虚数部に代入する
double[] Wave_Re = new double[Samples], Wave_Im = WaveSamples;
// ビット逆順をかけた波形データを実数部に入れ替える
// 入れ替えたデータはその都度クリアしていく
// ついでに窓関数をかけておく
for(int i = 0; i < Samples; i++) {
Wave_Re[i] = Wave_Im[Bitreverse[i]] * Window((double)Bitreverse[i] / Samples);
Wave_Im[Bitreverse[i]] = 0.0;
}
// バタフライ演算をする
for(int i = 1; i < Samples; i *= 2)
for(int j = 0; j < Samples; j += i * 2)
for(int k = 0; k < i; k++) {
int a = j + k;
int b = a + i;
int w = Samples / (2 * i) * k;
double
ar = Wave_Re[a] + Wave_Re[b] * Twiddle[0, w] - Wave_Im[b] * Twiddle[1, w],
ai = Wave_Im[a] + Wave_Re[b] * Twiddle[1, w] + Wave_Im[b] * Twiddle[0, w],
br = Wave_Re[a] - Wave_Re[b] * Twiddle[0, w] + Wave_Im[b] * Twiddle[1, w],
bi = Wave_Im[a] - Wave_Re[b] * Twiddle[1, w] - Wave_Im[b] * Twiddle[0, w];
Wave_Re[a] = ar;
Wave_Im[a] = ai;
Wave_Re[b] = br;
Wave_Im[b] = bi;
}
// 複素数形式の波形データの絶対値を返す
for(int i = 0; i < Samples; i++) Wave_Re[i] = Math.Sqrt(Wave_Re[i] * Wave_Re[i] + Wave_Im[i] * Wave_Im[i]);
return Wave_Re;
}
}
}
このプログラムを使えば、より速いオーディオビジュアライザを作ることができます。
今度こそ無事にフーリエ変換を実装することができました!!!
最後に
今回掲示したソースコードは、dllファイルとともにここからダウンロードできます。特に使用許可は必要ないので、使っていただければ幸いです。