Python: 離散フーリエ変換（実装コードとテスト）

離散フーリエ変換

参考 ⇒ wiki

離散フーリエ変換の式

${\displaystyle F(t)= \sum_{x=0}^{N-1} f(x) e^{-i\frac{2 \pi t x}{N}} \quad \quad }$

逆離散フーリエ変換の式

${f(x)={\displaystyle \frac {1}{N}}\sum _{{t=0}}^{{N-1}}F(t)e^{{i{\frac {2\pi xt}{N}}}}\quad \quad}$

実装したdftのコード

dft.py

import cmath

import numpy as np


def dft(f):
    N = len(f)
    A = np.arange(N)
    T = A.reshape(1, -1)
    X = A.reshape(-1, 1)
    # 行列演算形式になっているがwikiの数式そのまま
    M = f * cmath.e**(-1j * 2 * cmath.pi * T * X  / N)
    return np.sum(M, axis=1)


def idft(f):
    N = len(f)
    A = np.arange(N)
    X = A.reshape(1, -1)
    T = A.reshape(-1, 1)
    # 同上
    M = f * cmath.e**(1j * 2 * cmath.pi * X * T  / N)
    return np.sum(M, axis=1) / N


def dft_matrix(f):
    N = len(f)
    A = np.arange(N)
    T = A.reshape(1, -1)
    X = A.reshape(-1, 1)
    return cmath.e**(-1j * 2 * cmath.pi * T * X  / N)

テスト

実装コードをimportしてテスト.

%matplotlib inline

import dft
import numpy as np
import cmath
import matplotlib.pyplot as plt

# ステップ
s = 0.1
# 横軸(0~2πまで)
x = np.arange(0, 2 * cmath.pi, s)
y = np.sin(x) + 2 * np.sin(2 * x + cmath.pi)
fy = dft.dft(y)
yd = dft.idft(fy)
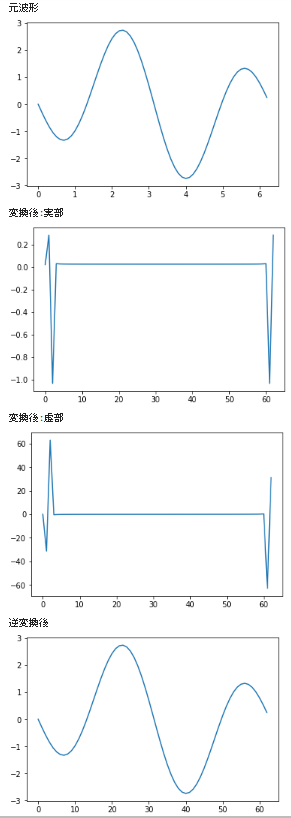
print('元波形')
plt.plot(x, y)
plt.show()
print('変換後:実部')
plt.plot(fy.real)
plt.show()
print('変換後:虚部')
plt.plot(fy.imag)
plt.show()
print('逆変換後')
plt.plot(yd.real)
plt.show()

変換と逆変換ができていることを確認.

追記

x,tの積部分はNxNパターンあるので, 以下のような行列演算で一気にやることができる.

A = np.arange(4)
A.reshape(1, -1) * A.reshape(-1, 1)

実行結果

array([[0, 0, 0, 0],
       [0, 1, 2, 3],
       [0, 2, 4, 6],
       [0, 3, 6, 9]])

追追記

よく見るとよくある行列用いた空間系の変換みたいにできそうなのでやってみた.
逆変換行列の作成方法が変なのと, 最後Nで割っているところは調整がいる.
⇒できたら今後「変換行列による離散フーリエ変換」みたいな記事書きたい.+.(ﾉ･ω･)ﾉ.

%matplotlib inline

import dft
import numpy as np
import cmath
import matplotlib.pyplot as plt

# ステップ
s = 0.1
# 横軸(0~2πまで)
x = np.arange(0, 2 * cmath.pi, s)
y = np.sin(x) + 2 * np.sin(2 * x + cmath.pi)
# 変換行列
M = dft_matrix(y)
# 波形 ⇒　M　⇒ 周波数表現
fy = np.dot(M, y)
# 周波数表現 ⇒　-M　⇒ 波形
yd = np.dot(-M, fy) / len(fy)
print('元波形')
plt.plot(x, y)
plt.show()
print('変換後:実部')
plt.plot(fy.real)
plt.show()
print('変換後:虚部')
plt.plot(fy.imag)
plt.show()
print('逆変換後')
plt.plot(yd.real)
plt.show()