$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
(先行研究リンク)
・Proceeding : https://dl.acm.org/citation.cfm?id=2927422
・発表動画 : https://vimeo.com/180284417
・QCEngine SIGGRAPH 2016 Examples : http://machinelevel.com/qc/siggraph/hello_siggraph_2016.html
・QCEngine Hands-On Introduction : http://machinelevel.com/qc/siggraph/qss_talk_slides.html
(作成したコード類＠GitHub)
・Pythonコード : QSSシミュレーション.ipynb
・QCEngine : QSS_QCEngine.cpp
(追記)
量子計算を用いて同様の積分計算を行うアルゴリズムを論文として発表しました：Quantum Coin Method for Numerical Integration (Computer Graphics Forum, 2020)。
Quantum Supersamplingのような深い量子回路を必要とする量子フーリエ変換を用いずに、小規模な量子回路を繰り返し実行する(量子古典ハイブリッド法)ことで、量子コンピュータ実機で不可避なエラーを低減する有効性を示しました。
概要
図のようにinput画像にフィルター処理を施す計算について考える。
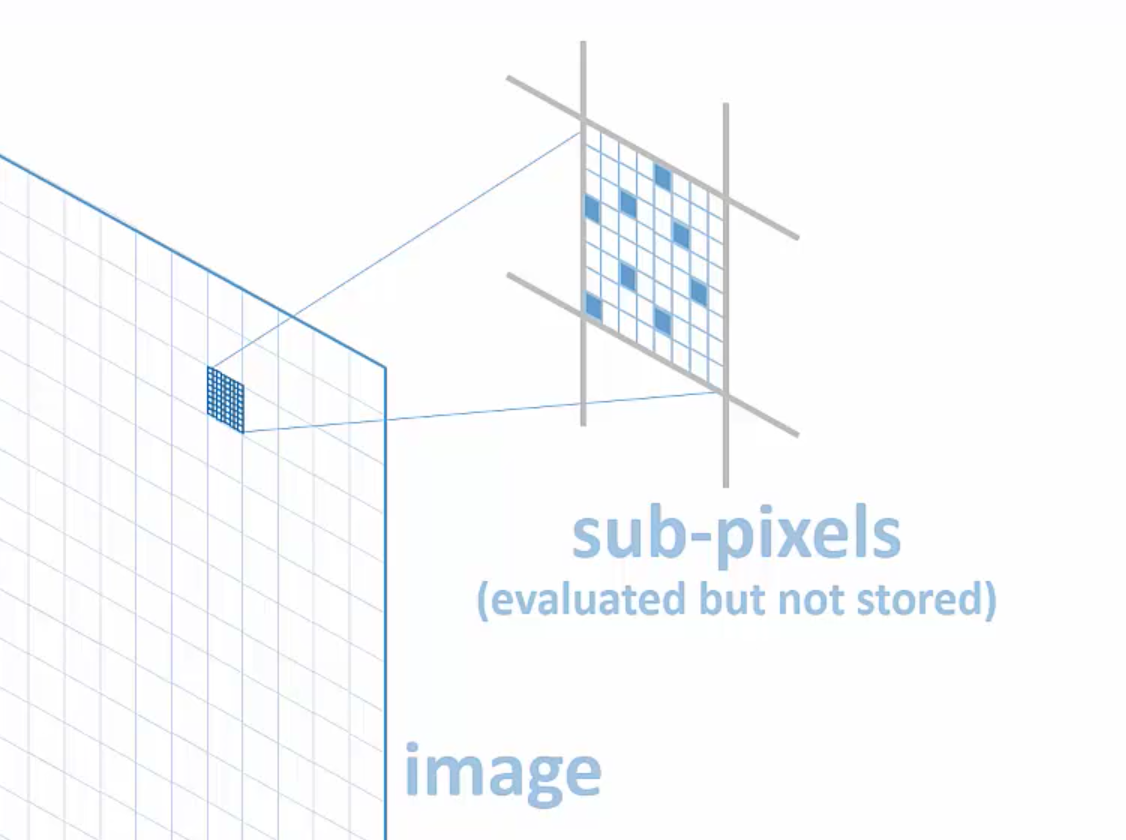複数のサブピクセルの平均値をまとめて一つのピクセル値で表すことでフィルター機能を実現している。通常はサブピクセル中の値をそのまま合計して平均値を計算すればよいが、例えばレイトレーシングによるCG画像生成においては全てのサブピクセル値について計算するのは大変なのでモンテカルロサンプリングによって考慮するサブピクセルの数を減らし高速化を図る。もちろん近似値しか得られなくなるが、サンプリング数を増やすことで統計的にground truthの値に近づいていく。
量子計算を上手いこと使うと、この平均値計算を行うことが出来、iteration(サンプリング数)vs合計エラー値という観点から見るとモンテカルロ計算よりもエラーを抑えることができるらしい。これをQuantum Supersamplingと呼ぶことにする。
モンテカルロsampling
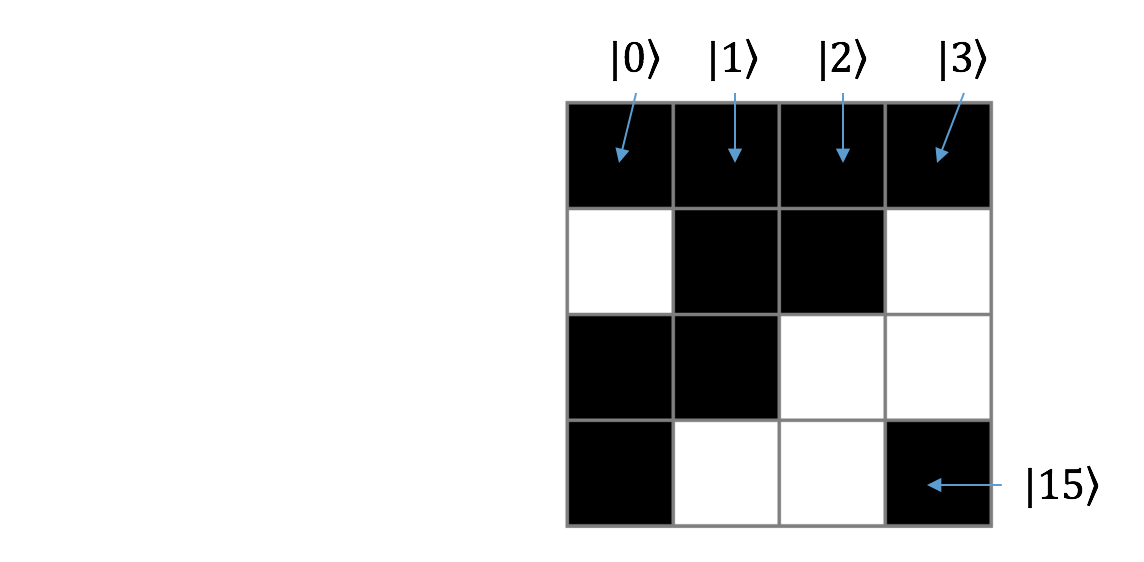
図のような16個のサブピクセルをまとめて1ピクセルで表現する状況を考える。今の場合、hit(白)が6個、no-hit(黒)が10個なので、ground truthの出力としては6/16となる。
モンテカルロサンプリングでは、サブピクセルからランダムに1つを抽出し、その値を合計していって平均値を推定する。
Quantum Supersampling
理論的背景(Shader,Grover,量子フーリエ変換)を追っていきながら、Pythonシミュレーションにより先行研究の図が再現できることを確認する。Lookup Tableを再現した後、その解釈方法について述べる。最後に量子回路シミュレーター(QCEngine)で先行研究の再現を行う。
Shader
QSSでは、16個のサブピクセルのデータ列が与えられた場合、それを量子状態$\ket{\psi}$
\begin{eqnarray}
\ket{\psi} = \frac{1}{4} (c_0 \ket{0} + c_1 \ket{1} + \cdots + c_{15} \ket{15} )
\end{eqnarray}
に対応させる。つまり、係数$c_n$の値(0,1)にピクセルの色(黒,白)を格納することで古典データを量子的なデータに変換する。ここで$\ket{0}\sim\ket{15}$は線形独立な量子状態であり、4つの量子ビットを用いて
\begin{eqnarray}
\ket{0} &=& \ket{\uparrow}_0 \otimes \ket{\uparrow}_1 \otimes \ket{\uparrow}_2 \otimes \ket{\uparrow}_3 \\
\ket{1} &=& \ket{\downarrow}_0 \otimes \ket{\uparrow}_1 \otimes \ket{\uparrow}_2 \otimes \ket{\uparrow}_3 \\
\ket{2} &=& \ket{\uparrow}_0 \otimes \ket{\downarrow}_1 \otimes \ket{\uparrow}_2 \otimes \ket{\uparrow}_3 \\
&\cdots& \\
\ket{15} &=& \ket{\downarrow}_0 \otimes \ket{\downarrow}_1 \otimes \ket{\downarrow}_2 \otimes \ket{\downarrow}_3
\end{eqnarray}
とする。
上図のような場合には、
\begin{eqnarray}
\ket{\psi} = \frac{1}{4} (-\ket{0} - \ket{1} - \ket{2} - \ket{3} + \ket{4} - \ket{5} - \ket{6} + \ket{7} - \ket{8} - \ket{9} + \ket{10} + \ket{11} - \ket{12} + \ket{13} + \ket{14} - \ket{15})
\end{eqnarray}
のようにno-hit(黒)に対応する状態の係数をマイナス1とする。QSSではこの量子状態$\ket{\psi}$からhit数(6個)を得るのが目的となる。
このようにno-hitの係数をマイナスにマーキングする操作をshaderと呼ぶ。
Groverアルゴリズム
特定の量子状態にマーキングをつけて、それを見つける探索アルゴリズムとしてはGroverアルゴリズムが存在する。「Groverアルゴリズム 自分用まとめ」に書いた通り、Groverアルゴリズムでは
・ Shader操作によるマーキング(=位相反転)
・ 平均値周りで反転
を交互に行うのであった。
具体的にhit数A=1の場合について計算してみると、
\begin{eqnarray}
\ket{\psi} &=& \frac{1}{4} (\ket{0} + \ket{1} + \cdots + \ket{15} ) \\
&\rightarrow& \frac{1}{4} (\ket{0} - \ket{1} - \cdots - \ket{15} ) \\
\end{eqnarray}
平均値は$(\frac{1}{4}+(-\frac{1}{4})*15)/16=-0.218\cdots$となり、(0.25, -0.25)をこの周りで逆転させると(-0.6875, -0.1875)となる。これを繰り返していくと
(0.25, 0.25)
(-0.6875, -0.1875)
(0.953125, 0.078125)
(-0.98046, 0.050781)
(0.762695, -0.166992)
(-0.35424, 0.2414550)
(-0.14276, -0.255554)
(0.604080, 0.2057647)
$\cdots$
のように振動する振る舞いが見られる。A=1と15の場合をグラフにプロットしてみると
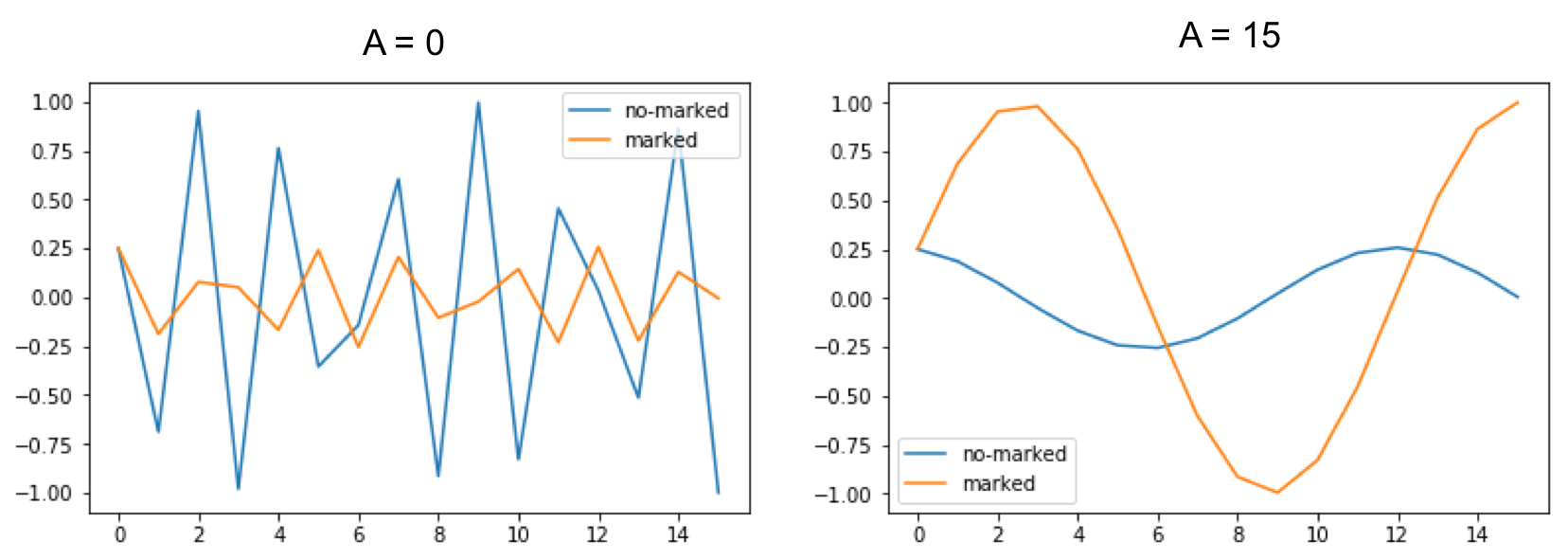
この繰り返し操作では明らかにhit数Aに依存して振動の振る舞いが変わり、またAの数が同一であればデータ列の並び順に依存しない。この性質は、逆に振動の振る舞いからAの値を一意に特定できる可能性を示唆している。振動の振る舞いをその周期性で特徴づけるならば、(量子)フーリエ変換によって周波数特性を見れば良さそうである。
$A=0\sim16$のすべての場合を計算して画像化すると、
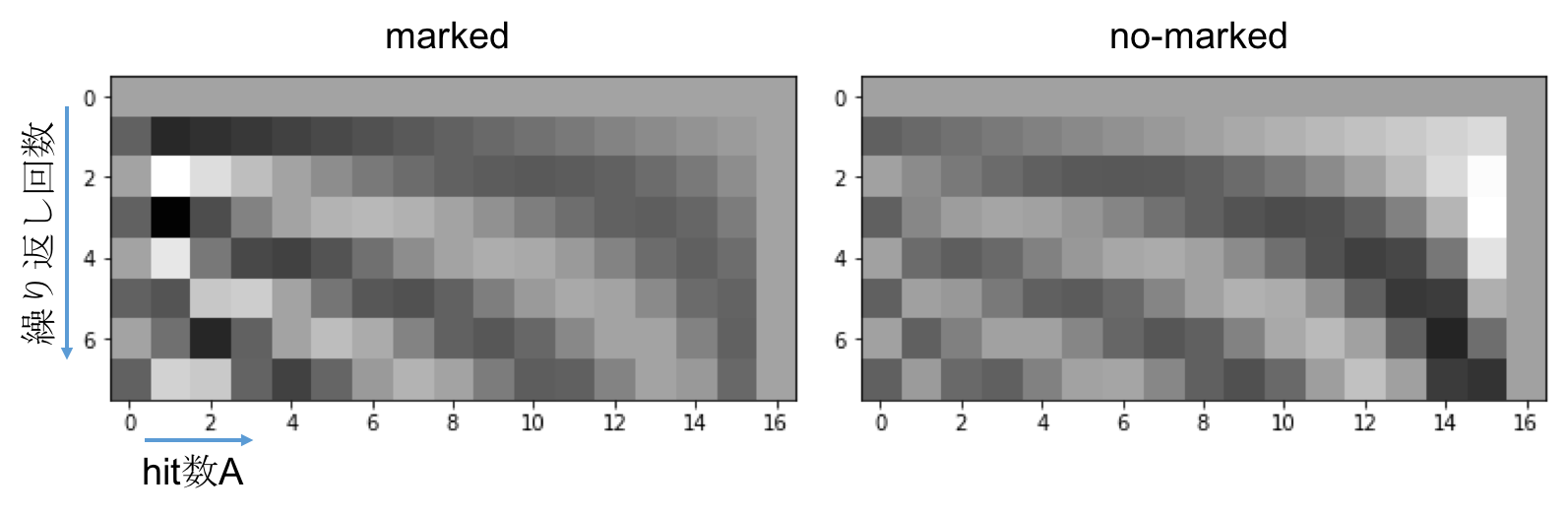
のようになる(黒:-1, 白:+1のグレースケールで値を表現している)。no-markedの方は先行研究の図と一致した。
使用したPythonコードは以下に載せておく。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
a = 8 # count_number
b = [1.0/4.0, 1.0/4.0]
print(b[0], b[1])
image0 = [b[0]]
image1 = [b[1]]
for i in range(15):
b[1] = -b[1]
average = a*b[0] + (16-a)*b[1]
average /= 16.0
#print(average)
b[0] = 2*average - b[0]
b[1] = 2*average - b[1]
print(b[0], b[1])
#print(abs(b[0]), abs(b[1]))
image0.append(b[0])
image1.append(b[1])
plt.plot(image0, label = "no-marked")
plt.plot(image1, label = "marked")
plt.legend()
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
n = 7
image = [[0.25] * 17 for i in range(n+1)]
image_marked = [[0.25] * 17 for i in range(n+1)]
for a in range(17):
b = [1.0/4.0, 1.0/4.0]
for i in range(n):
#print(a,i)
b[1] = -b[1]
average = a*b[0] + (16-a)*b[1]
average /= 16.0
b[0] = 2*average - b[0]
b[1] = 2*average - b[1]
image[i+1][a] = b[0]
image_marked[i+1][a] = b[1]
image[1][0] = -0.25
image[2][0] = 0.25
image[3][0] = -0.25
image[4][0] = 0.25
image[5][0] = -0.25
image[6][0] = 0.25
image[7][0] = -0.25
image_marked[1][16] = 0.25
image_marked[2][16] = 0.25
image_marked[3][16] = 0.25
image_marked[4][16] = 0.25
image_marked[5][16] = 0.25
image_marked[6][16] = 0.25
image_marked[7][16] = 0.25
#画像の表示
plt.imshow(image, cmap = 'gray', vmin = -1, interpolation = 'none')
plt.show()
plt.imshow(image_marked, cmap = 'gray', vmin = -1, interpolation = 'none')
plt.show()
量子逆フーリエ変換
上ではGroverアルゴリズムによって振動する値の周期性をフーリエ変換によって抽出することでhit数Aを特定できるのではないかと述べた。実際にフーリエ変換を行ってみる。フーリエ変換・逆フーリエ変換どちらでもよいはずであるが、今回は先行研究に合わせて逆フーリエの方を使用する。「量子フーリエ変換 自分用まとめ」の離散時間・離散周波数フーリエ変換から、離散逆フーリエ変換は次のような行列計算を行うだけでよい。
\begin{eqnarray}
\begin{pmatrix}
F_0 \\ F_1 \\ F_2 \\ \cdot \\ \cdot \\ \cdot \\ F_{N-1}
\end{pmatrix}
=
\frac{1}{\sqrt{N}}
\begin{pmatrix}
e^{i \frac{2\pi}{N} 0\cdot0} & e^{i \frac{2\pi}{N} 0\cdot1} & \cdot & \cdot & \cdot & e^{i \frac{2\pi}{N} 0\cdot (N-1)} \\
e^{i \frac{2\pi}{N} 1\cdot0} & e^{i \frac{2\pi}{N} 1\cdot1} \\
\cdot \\
\cdot \\
\cdot \\
e^{i \frac{2\pi}{N} (N-1)\cdot0} & \cdot & \cdot & \cdot& \cdot & \cdot
\end{pmatrix}
\begin{pmatrix}
f_0 \\ f_1 \\ f_2 \\ \cdot \\ \cdot \\ \cdot \\ f_{N-1}
\end{pmatrix}
\end{eqnarray}
maekedとno-markedの両方にフーリエ変換を施し、出てきた値をそれぞれの個数Aと16-Aの重みづけをして平均を取る。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
n = 3
image = [[100.0] * 17 for i in range(n+1)]
F_inv = np.array([[1, 1, 1, 1], [1, -1j, -1, 1j], [1, -1, 1, -1], [1, 1j, -1, -1j]])
F_inv /= 2.0
for a in range(17):
pre_QFT = [0.25]*(n+1)
pre_QFT_marked = [0.25]*(n+1)
b = [1.0/4.0, 1.0/4.0]
for i in range(n):
b[1] = -b[1]
average = a*b[0] + (16-a)*b[1]
average /= 16.0
b[0] = 2*average - b[0]
b[1] = 2*average - b[1]
pre_QFT[i+1] = b[0]
pre_QFT_marked[i+1] = b[1]
pre_QFT = np.array(pre_QFT)
temp = np.dot(F_inv, pre_QFT)
result = np.real(temp*np.conj(temp)) # 複素振幅の2乗を取る
pre_QFT_marked = np.array(pre_QFT_marked)
temp_marked = np.dot(F_inv, pre_QFT_marked)
result_marked = np.real(temp_marked*np.conj(temp_marked)) # 複素振幅の2乗を取る
result = (result*a + result_marked*(16-a))/16.0 # 平均 (=観測確率にあたる)
#for i in range(n+1):
# image[i][a] = result[i]
# (注意) SWAP操作
image[0][a] = result[0]
image[1][a] = result[2]
image[2][a] = result[1]
image[3][a] = result[3]
#画像の表示
plt.imshow(image, cmap = 'gray', vmin = 0, interpolation = 'none')
plt.show()
出力画像は次のようになる。各状態$\ket{0}\sim\ket{3}$の観測確率(複素振幅の絶対値2乗のmarked-no_marked平均)を黒:0,白:1のグレースケールで表現した。
先行研究のLookup Table:
先行研究図と一致した。(注意: 先行研究(で使用されているQCEngine)では量子逆フーリエ変換に最後のSWAP操作を含まないようになっている。上のPython計算では出力図の縦並びを揃えるためにSWAP変換を再び加えることでもとに戻す操作をしている。)
Lookup Tableの解釈
ここまでの議論から、Lookup Tableの意味するところは、例えばhit数$A=0$のサブピクセルを入力した場合には100%の確率で$\ket{1}$状態が観測され、hit数$A$=1のサブピクセルを入力した場合には約90%の確率で$\ket{1}$状態,その他低確率で$\ket{0},\ket{2},\ket{3}$観測されるということを示す。我々が量子計算の出力として得られるのは$\ket{0}\sim\ket{3}$のどの状態が観測されたかという情報のみである。もし状態$\ket{0}$が得られたならば$A=0$である可能性が高いが、$A=1,2,3$あたりの可能性も十分にある。QSSとしては最も可能性の高い$A=0$をFilterの結果として選ぶ。
3 iterationの表では観測結果から大まかなhit数は当てられるが、一意に$A$を当てられるほどではない。iterationの数を増やすことでよりA数による周波数特性の違いが明確になり$A$を特定する可能性が高まっていく。
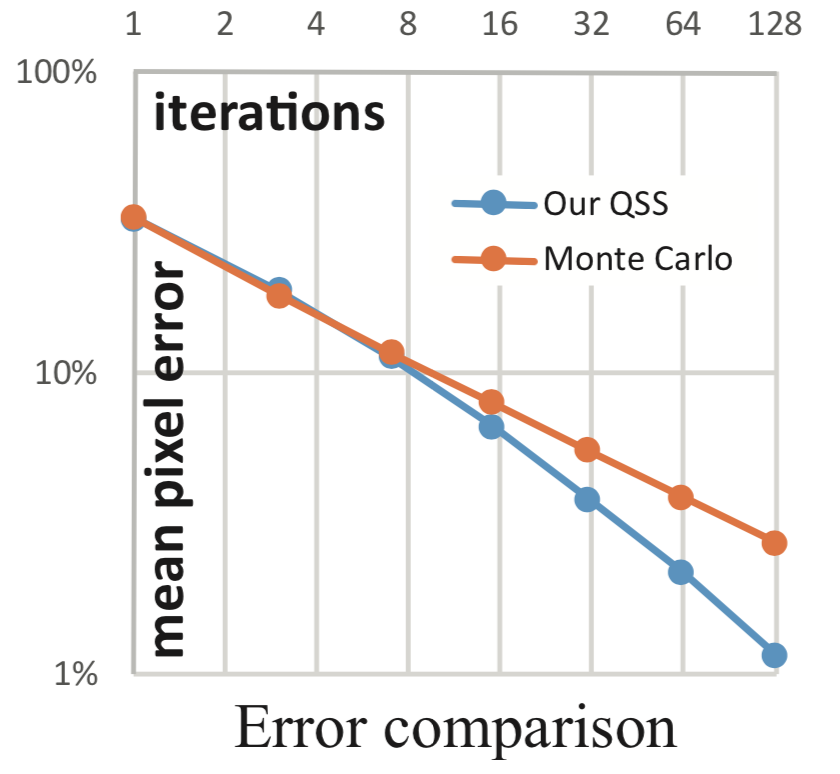
QSSでiterationを増やすことはモンテカルロサンプリングでサンプリング回数を増やすことに対応しているが、両者ではiterationに対するエラー確率の減少に異なる振る舞いが見られる。
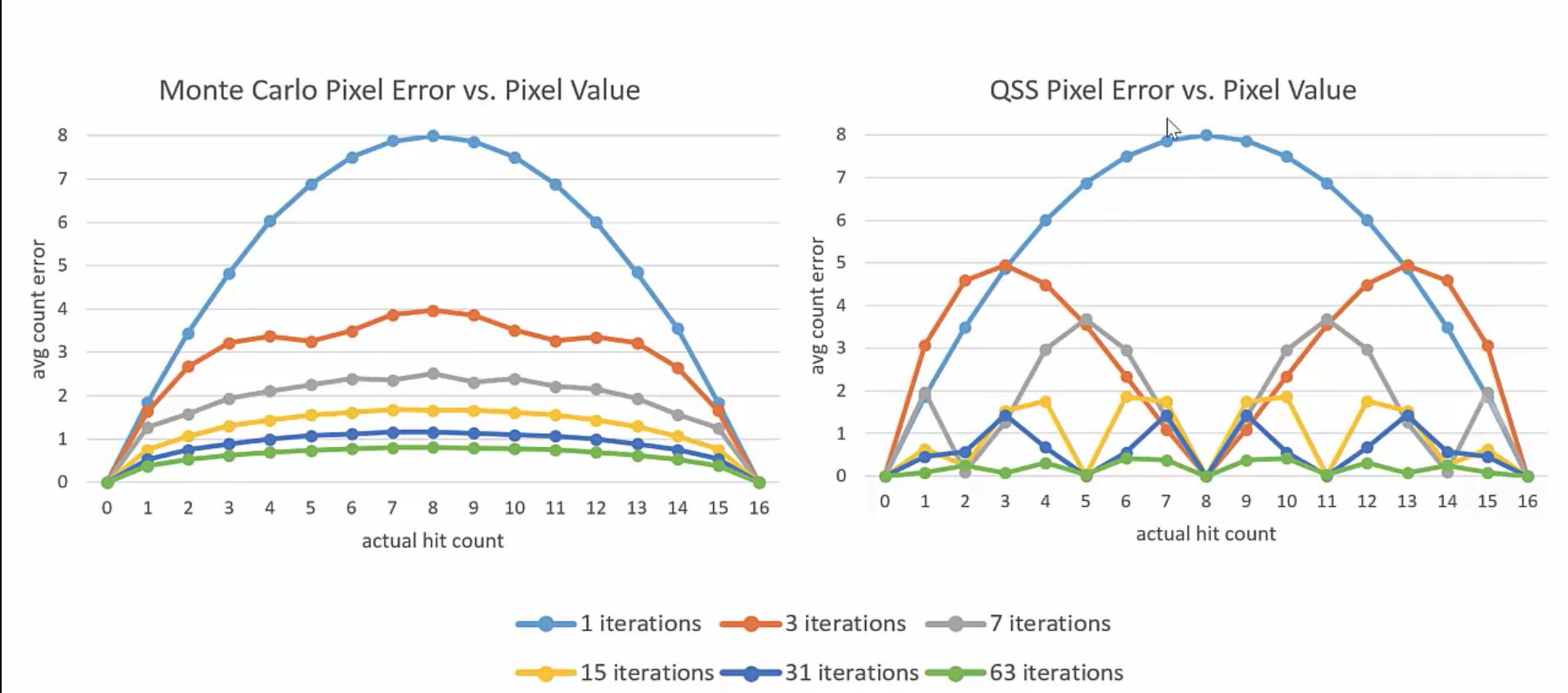
モンテカルロサンプリングではすべての$A$に対して同程度にエラーが減少していくのに対して、QSSでは特定の値を100%当てるようになっていくという特徴的な違いが見られる。
この性質は次のFiltered画像に現れている。モンテカルロでは全体的にぼやけた画像になっているのに対して、QSSではところどころに大きくhit数を外したエラーの痕跡が見て取れる。また、最右グラフにあるように、全体のエラー発生確率抑制はQSSの方が有利なようである。
問題点
・ shader操作にはそもそもサブピクセルの完全な白黒分布が必要である。それがわかっているならshaderを構成するより古典的に数え上げたほうが早い。レイトレーシングで毎回レイを飛ばしてピクセル値を計算するときのように分布がわかっていない場合には使えない。実用性に疑問
・hit数によって周期性が違って来ることを理論的根拠にしているが、あらゆる場合にこれが成立するのかはちょっと非自明な気がする...?
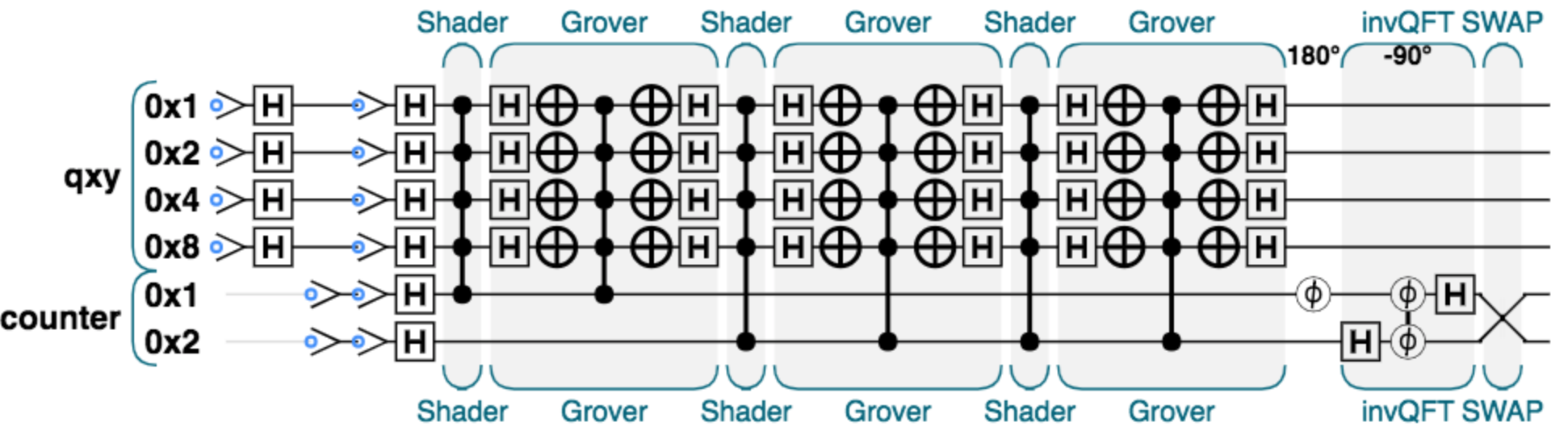
QCEngineでの実装
QCEngineを用いて量子回路でQuantum Samplingを実装してみる。「QCEngine Intro」を主に参照。
Shader
QCEngine Introのコードを元に実装方法を見る。下のコードを実行すると、
qc_options.color_by_phase = true;
qc_options.circle_scale = 0.5;
qc.reset(4);
qc.write(0);
// Just an example scene evaluation
function apply_shader()
{
}
qc.hadamard();
apply_shader();
ただアダマールゲートを作用させただけなので、すべての$\ket{n}$が等しく重ね合わさった量子状態が得られる。
\begin{eqnarray}
\ket{\psi} = \frac{1}{4} (\ket{0} + \ket{1} + \cdots + \ket{15} )
\end{eqnarray}
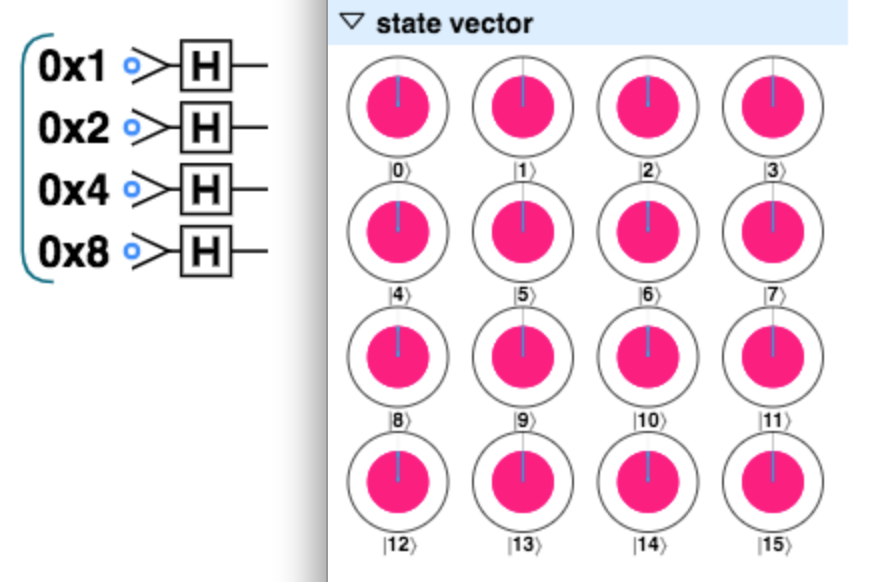これはすべてのサブピクセルがhit(白)つまり$A=16$の場合にあたる(先行研究ではこれをすべてno-hit(黒)という逆位相で定義をしているが、これは間違い。後に見るGroverアルゴリズムにおいて位相反転を考慮しないというミスをしているため1周して辻褄があってしまっている)。
任意のshaderを作るにはapply_shader()関数内にそれを定義する。1状態だけ位相反転させるには、controlled-Phaseシフトゲート(controllビットが全て$\ket{\downarrow}$の時に、対象のbitを位相反転する):qc.phase(180, 1|2|4|8);を作用させればよい。
\begin{eqnarray}
\ket{15} &=& \ket{\downarrow} \otimes \ket{\downarrow} \otimes \ket{\downarrow} \otimes \ket{\downarrow} \\
&\rightarrow& - \ket{\downarrow} \otimes \ket{\downarrow} \otimes \ket{\downarrow} \otimes \ket{\downarrow}
\end{eqnarray}
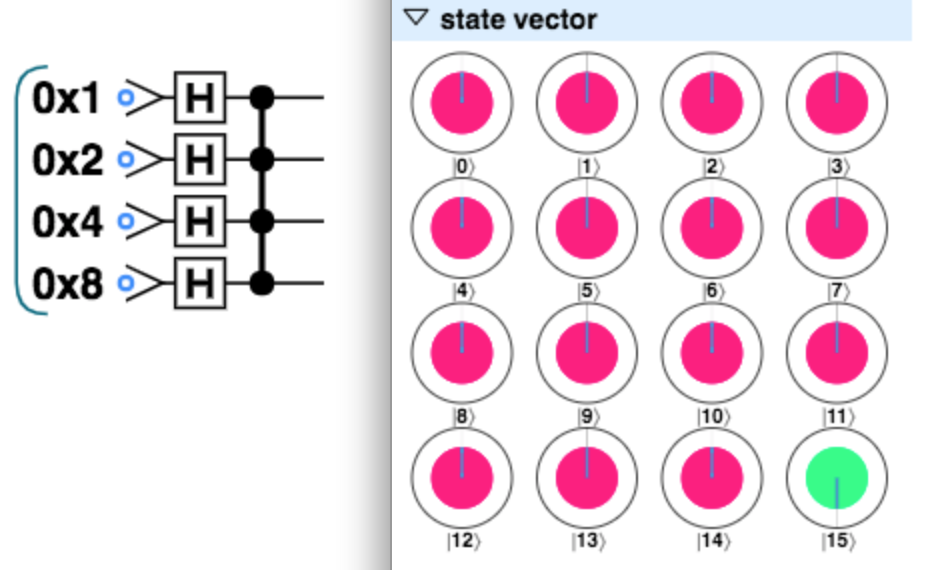のように変化する。
全ての場合をまとめると、
・$A=16$ ($0$反転) : 無し
・$A=15$ ($1$反転) : qc.phase(180, 1|2|4|8);
・$A=14$ ($2$反転) : qc.phase(180, 1|2|4);
・$A=12$ ($4$反転) : qc.phase(180, 1|2);
・$A=10$ ($6$反転) : qc.phase(180, 1|2); qc.phase(180, 4|8);
・$A=8$ ($8$反転) : qc.phase(180, 1);
・$A=1\sim7$ ($9\sim15$反転) : 下の$A=0$から適当に文尾のqc.not(8);を消去する得られる。
・$A=0$ ($16$反転) :
qc.phase(180, 1|2|4|8); qc.not(8); qc.phase(180, 1|2|4|8); qc.not(8);
qc.not(2); qc.phase(180, 1|2|4|8); qc.not(8); qc.phase(180, 1|2|4|8); qc.not(8);
qc.not(4); qc.phase(180, 1|2|4|8); qc.not(8); qc.phase(180, 1|2|4|8); qc.not(8);
qc.not(2); qc.phase(180, 1|2|4|8); qc.not(8); qc.phase(180, 1|2|4|8); qc.not(8);
qc.not(4);
qc.not(1); qc.phase(180, 1|2|4|8); qc.not(8); qc.phase(180, 1|2|4|8); qc.not(8);
qc.not(2); qc.phase(180, 1|2|4|8); qc.not(8); qc.phase(180, 1|2|4|8); qc.not(8);
qc.not(4); qc.phase(180, 1|2|4|8); qc.not(8); qc.phase(180, 1|2|4|8); qc.not(8);
qc.not(2); qc.phase(180, 1|2|4|8); qc.not(8); qc.phase(180, 1|2|4|8); qc.not(8);
qc.not(4);
qc.not(1);
Grover
Shader関数の後にGrover関数を作用させる。QCEngineで定義されたGrover関数qc.Grover();は平均値周りでの反転操作$\hat{D}$(「Groverアルゴリズム 自分用まとめ」を参照)
\begin{eqnarray}
\hat{D} &=& -\hat{1} + 2\ket{\phi_0}\bra{\phi_0} \\
&=& -\hat{1} + 2 \hat{U} \ket{0} \bra{0} \hat{U}^{\dagger} \\
&=& -\hat{U} (\hat{1} - 2\ket{0} \bra{0}) \hat{U}^{\dagger}
\end{eqnarray}
のうち、$\hat{U} (\hat{1} - 2\ket{0} \bra{0}) \hat{U}^{\dagger}$の部分しか実装されていない。つまり、マイナスの位相反転項を自分で追加しなければならない(Shader関数で位相反転を逆に定義していたので結局辻褄は合う。同じ定義でLookup Tableを作成して、それを元にQSSを行うのであれば得られる結果は同じになるが)。
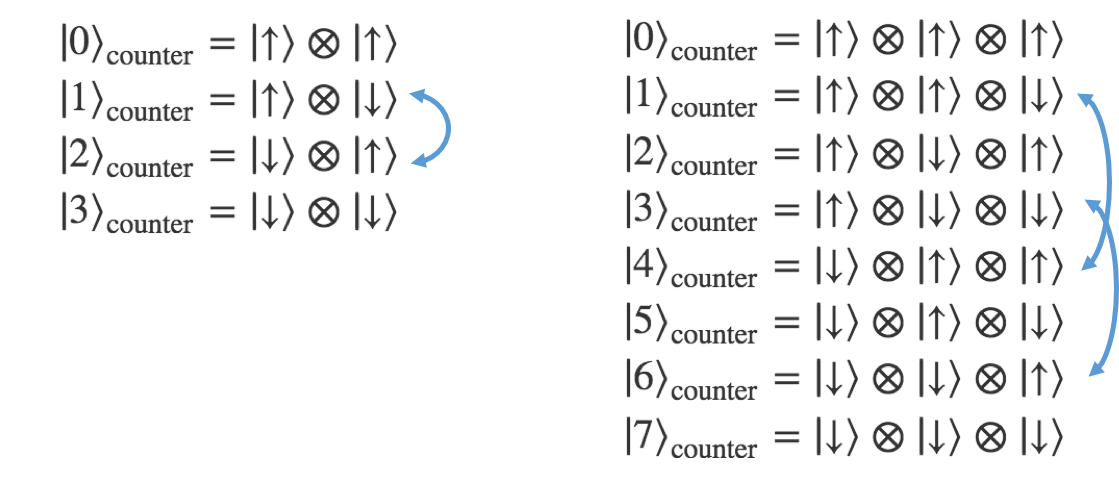
後はShader関数とGrover関数を交互に作用させていく。ただし最後に行う量子フーリエ変換のために、iterationごとの結果を保持しておく必要がある。よって、別途counterビットを用意し上手いこと結果を順番に保存するようにする。$A=15$の場合の量子回路は次のようになる。
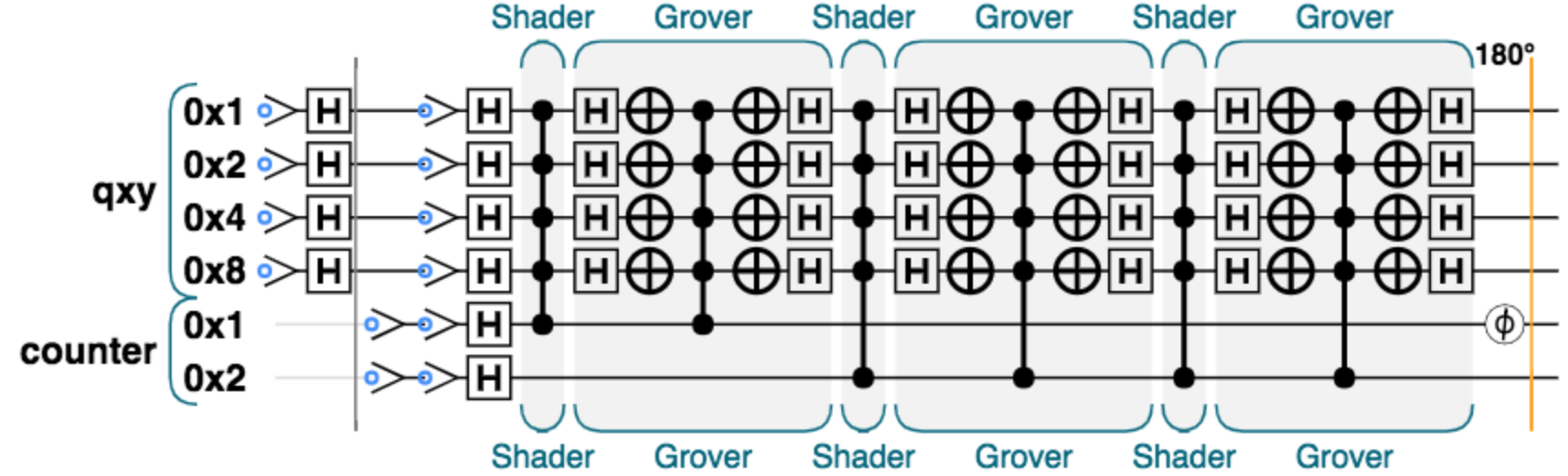
counterビットが2つなので、(保持できるiterationは合計$2^2=4$、初期状態を除けば)3 iterationを扱える。回路図では確かにshaderとGroverを3回繰り返している。QCEngineのGrover関数に位相反転が実装されていない問題は、最終的に奇数回目の結果だけを位相反転することで解決する。よって最後にcounterビットの1つめを$180$度シフトさせた。
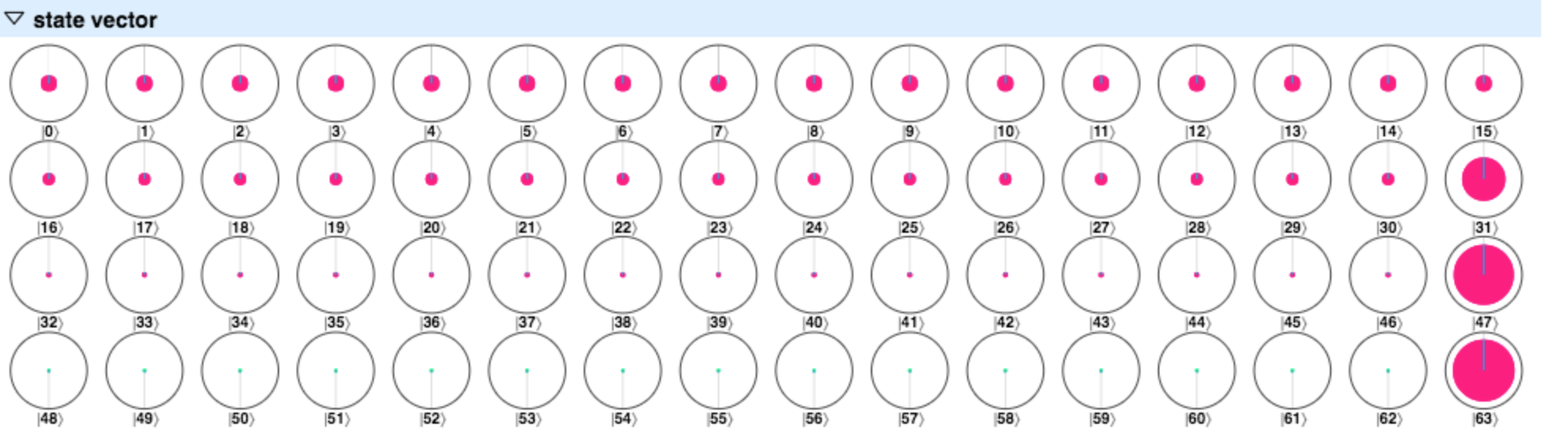
最終状態のstate vectorはこのようになる。4列に並んだうち、一番上が初期状態で、次が1 iteration後、・・・のように続いていく。あとは、このデータ列を縦方向(counterビット)に対して量子フーリエ変換を行う。
qc_options.color_by_phase = true;
qc_options.circle_scale = 0.5;
var qxy_bits = 4;
var counter_bits = 2;
qc.reset(qxy_bits + counter_bits);
var qxy = qint.new(qxy_bits, 'qxy');
var counter = qint.new(counter_bits, 'counter');
qxy.write(0);
qxy.hadamard();
counter.write(0);
// Just an example scene evaluation
function apply_shader2(target, condition)
{
target.phase(180, 1|2|4|8, condition); // A=15
// A=16 0: なし
// A=15 1: target.phase(180, 1|2|4|8, condition);
// A=14 2: target.phase(180, 1|2|4, condition);
// A=12 4: target.phase(180, 1|2, condition);
// A=10 6: QCEngine
// A=8 8: target.phase(180, 1, condition); target.phase(180, 2, condition);
/* A=0 16:
target.phase(180, 1|2|4|8, condition); target.not(8); target.phase(180, 1|2|4|8, condition); target.not(8);
target.not(2); target.phase(180, 1|2|4|8, condition); target.not(8); target.phase(180, 1|2|4|8, condition); target.not(8);
target.not(4); target.phase(180, 1|2|4|8, condition); target.not(8); target.phase(180, 1|2|4|8, condition); target.not(8);
target.not(2); target.phase(180, 1|2|4|8, condition); target.not(8); target.phase(180, 1|2|4|8, condition); target.not(8);
target.not(4);
target.not(1); target.phase(180, 1|2|4|8, condition); target.not(8); target.phase(180, 1|2|4|8, condition); target.not(8);
target.not(2); target.phase(180, 1|2|4|8, condition); target.not(8); target.phase(180, 1|2|4|8, condition); target.not(8);
target.not(4); target.phase(180, 1|2|4|8, condition); target.not(8); target.phase(180, 1|2|4|8, condition); target.not(8);
target.not(2); target.phase(180, 1|2|4|8, condition); target.not(8); target.phase(180, 1|2|4|8, condition); target.not(8);
target.not(4);
target.not(1);
*/
}
function do_iterations(target, counter, shader_func)
{
var eval_count = 0;
for (var bit = 0; bit < counter.numBits; ++bit)
{
for (var iter = 0; iter < (1 << bit); ++iter)
{
qc.codeLabel('Shader');
shader_func(target, counter.bits(1 << bit));
qc.codeLabel('Grover');
qxy.Grover(counter.bits(1 << bit));
qc.codeLabel('');
}
}
}
qc.write(0);
qc.hadamard();
do_iterations(qxy, counter, apply_shader2);
counter.phase(180,1); // (注意!!) これ絶対必要
量子逆フーリエ変換
counterビットに対して量子逆フーリエ変換(invQFT)を作用させる(QCEngineでは$e^{-ikx}$の方を順変換として定義している)。
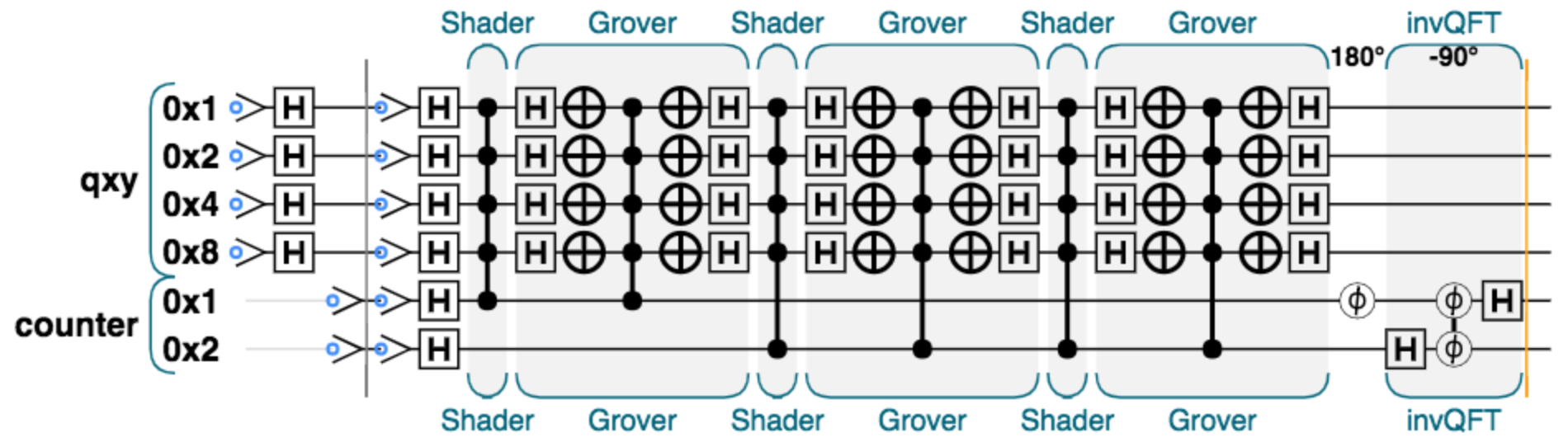
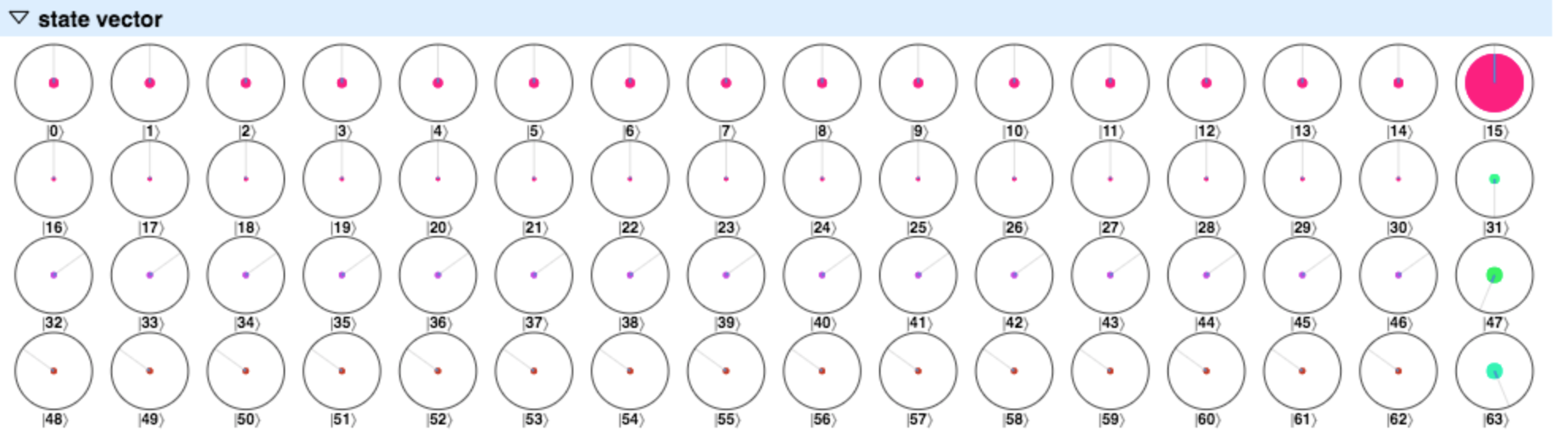
invQFTを作用させるとstate vectorは上図のようになる。ここでcounterビットの観測を行えば、一番上の状態$\ket{0}^{\mathrm{counter}}$が約90%程度の確率で出力されることになる。低確率で$\ket{2}^{\mathrm{counter}}$$\ket{3}^{\mathrm{counter}}$が、さらに低確率で$\ket{1}^{\mathrm{counter}}$が出力される可能性もある。
この結果は先行研究のLookup Tableとも一致している。
量子逆フーリエ変換では本来最後に全ビットの順番を入れ替えるSWAP操作が必要となる(量子フーリエ変換 自分用まとめ)。SWAP操作counter.exchange();を行った場合、
$\ket{2}^{\mathrm{counter}}$と$\ket{3}^{\mathrm{counter}}$が入れ替わる。Pythonでの数値シミュレーションにおいては結果をあわせるためにデータ列の操作(SWAPゲートを正味2回作用させる)を行ったが、本来の出力結果はこれに対応する。SWAP操作によるcounter状態の変化対応表を載せておく。
