$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
量子フーリエ変換(QFT)の自分用まとめ。フーリエ級数展開、フーリエ変換、離散フーリエ変換、量子フーリエ変換。
フーリエ級数展開
- フーリエ級数展開 ($-\pi\sim\pi$の周期2$\pi$)
\begin{eqnarray}
f(t) = \frac{a_0}{2} + \sum_{n=1}^{\infty} [a_n \mathrm{cos}(nt) + b_n \mathrm{sin}(nt)] \\
a_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(t) \mathrm{cos}(nt) dt \\
b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(t) \mathrm{sin}(nt) dt
\end{eqnarray}
- 複素フーリエ級数展開 ($-\pi\sim\pi$の周期2$\pi$)
\begin{eqnarray}
f(t) = \sum_{n=-\infty}^{\infty} c_n e^{int} \\
c_n = \frac{1}{2\pi} \int_{-\pi}^{\pi} f(t) e^{-int} dt
\end{eqnarray}
- 複素フーリエ級数展開 ($-L\sim L$の周期2$L$)
\begin{eqnarray}
f(t) = \sum_{n=-\infty}^{\infty} c_n e^{i\frac{n\pi}{L}t} \\
c_n = \frac{1}{2L} \int_{-L}^{L} f(t) e^{-i\frac{n\pi}{L}t} dt
\end{eqnarray}
フーリエ変換
「フーリエ級数とフーリエ展開」を参照。
$L\rightarrow \infty$で無限周期関数を扱えるようにするよ
まず$c_n$を代入して、
\begin{eqnarray}
f(t) = \sum_{n=-\infty}^{\infty} \frac{1}{2L} \int_{-L}^{L} f(t') e^{-i\frac{n\pi}{L}t'} dt' \, e^{i\frac{n\pi}{L}t}
\end{eqnarray}
$\omega_n = \frac{n\pi}{L}$ として、$\frac{1}{2L} = \frac{1}{2\pi} (\omega_{n+1}-\omega_{n}) \simeq \frac{1}{2\pi} d\omega$により、
\begin{eqnarray}
f(t) &=& \sum_{n=-\infty}^{\infty} \frac{d\omega}{2\pi} \int_{-\infty}^{\infty} f(t') e^{-i\omega t'} dt' \, e^{i\omega t} \\
&=& \frac{1}{2\pi} \int_{-\infty}^{\infty} [\int_{-\infty}^{\infty} f(t') e^{-i\omega t'} dt'] e^{i\omega t} d\omega
\end{eqnarray}
級数展開の式における周波数成分$c_n$にあたる部分を抜き出して、
\begin{eqnarray}
F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i\omega t} dt
\end{eqnarray}
これがフーリエ変換の式となる。
離散フーリエ変換
- 離散時間フーリエ変換
「5. 離散時間フーリエ変換」を参照。
関数$f(t)$が離散的である場合を考える。デルタ関数を用いて
\begin{eqnarray}
f(t) = \sum_{n=-\infty}^{\infty} f[n] \delta(t-n)
\end{eqnarray}
と表すと、
\begin{eqnarray}
F(\omega) &=& \int_{-\infty}^{\infty} f(t) e^{-i\omega t} dt \\
&=& \int_{-\infty}^{\infty} \sum_{n=-\infty}^{\infty} f[n] \delta(t-n) e^{-i\omega t} dt \\
&=& \sum_{n=-\infty}^{\infty} f[n] \int_{-\infty}^{\infty} \delta(t-n) e^{-i\omega t} dt \\
&=& \sum_{n=-\infty}^{\infty} f[n] e^{-i\omega n}
\end{eqnarray}
逆変換は、一周期のみ積分で
\begin{eqnarray}
f[n] = \frac{1}{2\pi} \int_{-\pi}^{\pi} F(\omega) e^{i \omega n} d\omega
\end{eqnarray}
- 離散時間・離散周波数フーリエ変換
「6. 離散フーリエ変換」を参照。
離散時間フーリエ変換では、離散信号$f(x)$から周期$2\pi$の連続周期信号$F(\omega)$が生成された。逆変換では$F(\omega)\rightarrow f(x)$であるが積分計算を行うことになる。これを避けるために$F(\omega)$も離散的であるような変換が欲しい。離散信号$f(x)$を定義域外で周期的に続いていく信号と考える。周期N点の離散信号$f(x)$は周期$2\pi$の離散信号$F(\omega)$に変換される。$F(\omega)$は$\frac{2\pi}{N}$間隔で離散化される。

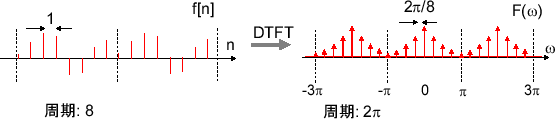
離散周期信号$F(\omega) = \sum_{k=-\infty}^{\infty} c_k \delta (\omega-\frac{2\pi k}{N})$と表すと、逆変換は
\begin{eqnarray}
f[n] &=& \frac{1}{2\pi} \int_{-\pi}^{\pi} \sum_{k=-\infty}^{\infty} c_k \delta(\omega - \frac{2\pi k}{N}) e^{i\omega n} d\omega \\
&=& \frac{1}{2\pi} \sum_{k=0}^{N-1} c_k e^{i \frac{2\pi kn}{N}} \\
&=& \frac{1}{N} \sum_{k=0}^{N-1} F[k] e^{i \frac{2\pi kn}{N}} \,\,\, (n = 0, 1, \cdots , N-1) \\
\end{eqnarray}
順変換は、
\begin{eqnarray}
F[k] &=& \sum_{n=0}^{N-1} f[n] e^{-i \frac{2\pi kn}{N}} \,\,\, (k = 0, 1, \cdots , N-1)
\end{eqnarray}
順変換を行列表記すると、
\begin{eqnarray}
\begin{pmatrix}
F_0 \\ F_1 \\ F_2 \\ \cdot \\ \cdot \\ \cdot \\ F_{N-1}
\end{pmatrix}
=
\frac{1}{\sqrt{N}}
\begin{pmatrix}
e^{-i \frac{2\pi}{N} 0\cdot0} & e^{-i \frac{2\pi}{N} 0\cdot1} & \cdot & \cdot & \cdot & e^{-i \frac{2\pi}{N} 0\cdot (N-1)} \\
e^{-i \frac{2\pi}{N} 1\cdot0} & e^{-i \frac{2\pi}{N} 1\cdot1} \\
\cdot \\
\cdot \\
\cdot \\
e^{-i \frac{2\pi}{N} (N-1)\cdot0} & \cdot & \cdot & \cdot& \cdot & \cdot
\end{pmatrix}
\begin{pmatrix}
f_0 \\ f_1 \\ f_2 \\ \cdot \\ \cdot \\ \cdot \\ f_{N-1}
\end{pmatrix}
\end{eqnarray}
量子フーリエ変換
「量子コンピュータ入門(宮野+古澤)」、「量子フーリエ変換 (Quantum Fourier Transform) とは」を参照。
目標
まず離散フーリエ変換を少し定義し直す(上2つの文献ではマイナス無しの方を順変換扱いしている、QCEngineではマイナスの方を順変換使いしてしているので注意)。
\begin{eqnarray}
F_k &=& \frac{1}{\sqrt{N}} \sum_{n=0}^{N-1} f_n e^{i \frac{2\pi kn}{N}} \,\,\, (k = 0, 1, \cdots , N-1)
\end{eqnarray}
量子フーリエ変換で目指すところは、ある量子状態$\ket{x}$
\begin{eqnarray}
\ket{x} &=& x_0\ket{00}+x_1\ket{01}+x_2\ket{10}+x_3\ket{11} \\
&=& x_0\ket{0}+x_1\ket{1}+x_2\ket{2}+x_3\ket{3} \\
&=& \sum_{j=0}^{N-1} x_j \ket{j}
\end{eqnarray}
が量子回路に入力されたとして、$x_j$の数値列$[x_0, x_1, x_2, x_3, \cdots]$を離散フーリエ変換した数値列$y_k=[y_0, y_1, y_2, y_3, \cdots]$
\begin{eqnarray}
y_k &=& \frac{1}{\sqrt{N}} \sum_{j=0}^{N-1} x_j e^{i \frac{2\pi kj}{N}}
\end{eqnarray}
を求めることである。直接$y_k$を出力することは出来ないので、出力が
\begin{eqnarray}
\ket{y} &=& \sum_{k=0}^{N-1} y_k \ket{k}
\end{eqnarray}
となるように基底$\ket{j}$を$\ket{k}$に変換することを目標とする。
定義を代入すると、
\begin{eqnarray}
\ket{y} &=& \sum_{k=0}^{N-1} \frac{1}{\sqrt{N}} \sum_{n=0}^{N-1} x_j e^{i \frac{2\pi kj}{N}} \ket{k} \\
&=& \sum_{n=0}^{N-1} x_j \{ \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} e^{i \frac{2\pi kj}{N}} \ket{k}\} \\
となり、\\
\ket{x} &=& \sum_{j=0}^{N-1} x_j \ket{j}
\end{eqnarray}
と見比べると、
\begin{eqnarray}
\ket{j} \rightarrow \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} e^{i \frac{2\pi kj}{N}} \ket{k}\
\end{eqnarray}
の基底変換が達成出来れば、自動的に$\ket{y}$の係数$y_k$は$x_j$の離散フーリエ変換となることがわかる。
アルゴリズムの導出
$N=2^n$とする。状態$\ket{k} = \ket{k_0} \otimes \ket{k_1} \otimes \ket{k_2} \cdots \otimes \ket{k_{n-1}}$のn個量子ビットで表現されているとし、$k=2^{n-1}k_{n-1}+ \cdots + 2^0k_0$の2進数に対応すると決める(古澤本では並びが逆)。
\begin{eqnarray}
\ket{j} &\rightarrow& \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} e^{i \frac{2\pi kj}{N}} \ket{k} \\
&=& \frac{1}{\sqrt{2^n}} \sum_{k=0}^{2^n-1} e^{i \frac{2\pi kj}{2^n}} \ket{k} \\
&=& \frac{1}{\sqrt{2^n}} \sum_{k_0=0}^{1} \sum_{k_1=0}^{1} \cdots \sum_{k_{n-1}=0}^{1} e^{i \frac{2\pi}{2^n}j(2^{n-1}k_{n-1}+ \cdots + 2^0k_0)} \ket{k_0} \otimes \ket{k_1} \otimes \ket{k_2} \cdots \otimes \ket{k_{n-1}} \\
&=& \frac{1}{\sqrt{2^n}} (\sum_{k_0=0}^{1} e^{i \frac{2\pi}{2^n}j(2^0k_0)} \ket{k_0}) \otimes \cdots \otimes (\sum_{k_0=0}^{1} e^{i \frac{2\pi}{2^n}j(2^{n-1}k_{n-1})} \ket{k_{n-1}}) \\
&=& \frac{1}{\sqrt{2^n}} (\ket{0} + e^{i2\pi \frac{j}{2^n}} \ket{1}) \otimes \cdots \otimes (\ket{0} + e^{i2\pi \frac{j}{2}} \ket{1}) \\
&=& \frac{1}{\sqrt{2^n}} (\ket{0} + e^{i2\pi 0.j_{n-1}j_{n-2}\cdots j_0} \ket{1}) \otimes \cdots \otimes (\ket{0} + e^{i2\pi 0.j_0}\ket{1} ) \\
\end{eqnarray}
ここで、$j$(10進数)$=j_{n-1}j_{n-2}\cdots j_0$(2進数)であり、例えば$j/2$(10進数)$=j_{n-1}.j_{n-2}\cdots j_0$(2進数)で整数部分は$e^{i2\pi}$によって消滅して少数部分が残る事実を使った。
量子回路での実装
- 1qubitの場合
n=1、$\ket{j}=\ket{j_0}$であり、
\begin{eqnarray}
\ket{j_0} \rightarrow \frac{1}{\sqrt{2}} (\ket{0} + e^{i2\pi 0.j_0}\ket{1})
\end{eqnarray}
つまり、
\begin{eqnarray}
\ket{0} \rightarrow \frac{1}{\sqrt{2}} (\ket{0} + \ket{1}) \\
\ket{1} \rightarrow \frac{1}{\sqrt{2}} (\ket{0} - \ket{1})
\end{eqnarray}
を実現すればよい。アダマールゲートのみで一発。
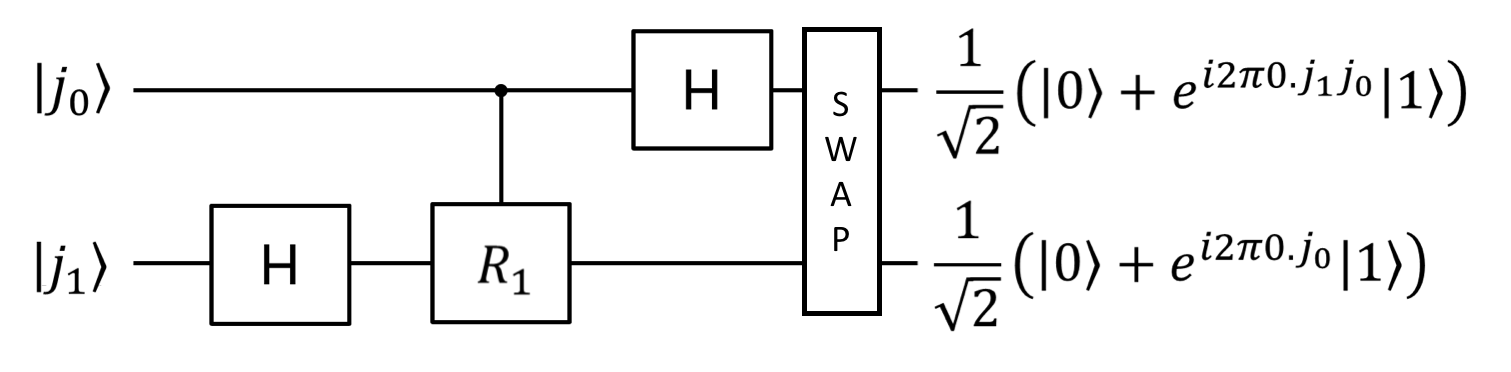
- 2qubitの場合
\begin{eqnarray}
\ket{j_0} \otimes \ket{j_1} \rightarrow \frac{1}{2} (\ket{0} + e^{i2\pi 0.j_1j_0}\ket{1}) \, (\ket{0} + e^{i2\pi 0.j_0}\ket{1})
\end{eqnarray}
を実現すればよい。
まずは$j_1$に対してアダマールゲートをかけると、
\begin{eqnarray}
\ket{j_0} \otimes \ket{j_1} \rightarrow \frac{1}{\sqrt 2} \ket{j_0} \otimes (\ket{0} + e^{i2\pi 0.j_1}\ket{1})
\end{eqnarray}
次に$j_0$が1の時に位相ファクター$e^{i2\pi/4}$を$j_1$に作用させるようなcontrolled-R1ゲートを作用させると$0.j_1j_0$が作れる、
\begin{eqnarray}
\ket{j_0} \otimes \ket{j_1} \rightarrow \frac{1}{\sqrt 2} \ket{j_0} \otimes (\ket{0} + e^{i2\pi 0.j_1j_0}\ket{1})
\end{eqnarray}
あとは$j_0$にアダマールゲートをかけると
\begin{eqnarray}
\ket{j_0} \otimes \ket{j_1} \rightarrow \frac{1}{\sqrt 2} (\ket{0} + e^{i2\pi 0.j_0}\ket{1}) \otimes (\ket{0} + e^{i2\pi 0.j_1j_0}\ket{1})
\end{eqnarray}
順番が逆転しているのでSWAPゲートを最後にかける。
- QCEngineでの回路実装
QCEngineでは逆QFTが$e^{ikx}$の方に対応しているので注意。また、関数として用意されている.QFT();および.invQFT();はswap変換を行ってくれないので手動で行う必要がある。
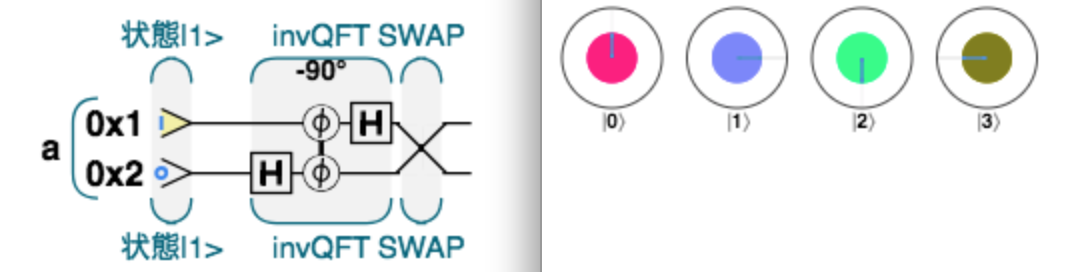
以下にQCEngineで使用したコードを示す。
qc_options.color_by_phase = true;
qc.reset(2);
var a = qint.new(2, 'a');
qc.codeLabel('状態|1>');
a.write(1);
qc.codeLabel();
qc.nop();
qc.codeLabel('invQFT');
a.invQFT();
qc.codeLabel();
qc.codeLabel('SWAP');
a.exchange();
qc.codeLabel();