神経回路シミュレーション (Python実装)

　今回は「はじめての神経回路シミュレーション (森北出版)」を読んで、自身でPython実装を行ったのでその解説と共にまとめておく。公式で公開されているC言語による実装例(GitHub)も一部参考にした。

はじめに

　まずは、神経回路シミュレーションにおいて基礎となる「ニューロン」と「シナプス」のモデルについて導入する。

ニューロン

　「Hodgkin-Huxleyモデル (HHモデル)」では、イオンチャネルを流れる膜電流を上手くモデル化することで、膜電位の変化を再現できることを見た。具体的に、膜電位$V(t)$とイオンチャネルの伝導度パラメータ$n,m,h$の4変数を用いて、次のような時間発展方程式が導出されるのであった：

\begin{eqnarray}
I_{ext} = C_m \frac{dV(t)}{dt} + \bar{g}_K \cdot n^4 \cdot (V-E_{K}) + \bar{g}_{Na} \cdot m^3 \cdot h \cdot (V-E_{Na}) + \bar{g}_{L} \cdot (V-E_L)
\end{eqnarray} 

膜電位の特徴的な変化として次の4つを列挙しておく。
　① 外部電流によって膜電位上昇
　② 閾値を超えると脱分極
　③ 再分極
　④ 不能期

HHモデルでは確かに細胞膜電位の特徴を捉えることが出来ていたが、4変数を陽に扱うため計算が重く時間ステップを細かく取る必要があった。これから扱うような大規模な神経モデルでは、ニューロンが発火したかどうかが重要であり、イオンチャネルについては簡略化して計算量を大幅に減らしたモデルを使いたい。

「LIFモデル (Leaky Integrate-and-Fire model、積分発火型モデル)」では、膜電位$V(t)$のみの1変数でシミュレーションを行う。

\begin{align}
 \tau \frac{d V(t)}{dt} = - (V(t)-V_\mathrm{eq}) + R \cdot I_\mathrm{ext}(t)
\end{align}

これは 「①外部電流による膜電位上昇」のみを再現する微分方程式である。(例えば、$I_\mathrm{ext}$を定数とすると、$V(t)$について解くことが出来て $V(t) - V_\mathrm{eq} = e^{-\frac{t}{\tau}} R I_\mathrm{ext}(t)$、時間$\tau$で外部電流による電位に漸近していくことがわかる。)

②と③については、上式で膜電位$V(t)$が閾値$\theta$を超えた時点で人為的に膜電位を上昇・リセットさせる (変数$S(t)$は、時刻$t$でニューロンが脱分極しスパイクが発生したかどうかを表す。)：

\begin{align}
 \mathrm{if} \ (V(t) > \theta) : V(t) \leftarrow V_\mathrm{eq}, \ S(t) \leftarrow 1
\end{align}

このモデルでは、④不能期については考慮していない (取り入れる場合は人為的に遅延させればよい)

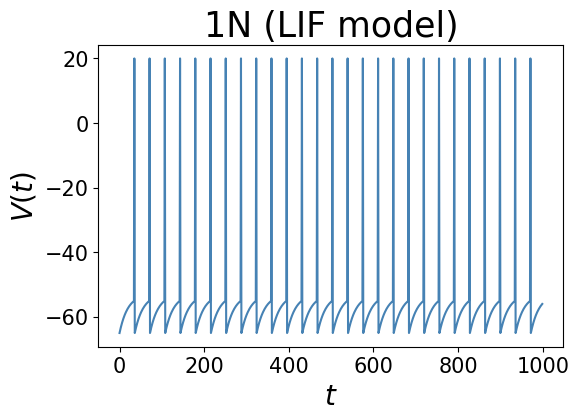
実際に数値シミュレーションした結果は以下のようになる。一定の外部電流が流され続けている1つのニューロンを想定し、膜電位の上昇・脱分極・再分極が再現されている。

実装例 (Python)

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline


T = 1000 # ms
dt = 1   # ms
num_t = int(T/dt) # ms
R = 1  # MΩ
I = 12 # nA
V_eq = -65.0  # mV
V_ex = 20.0   # mV
theta = -55.0 # mV
tau = 20 # ms


t_list = np.array([t*dt for t in range(num_t)])
V_list = np.zeros(num_t)
V_list[0] = V_eq


def LIF(V_prev, i_ext):
    if (V_prev>theta): # 前ステップで既に閾値θ超えてたら人為的にリセット
        return V_eq
    temp = - (V_prev - V_eq) + R*i_ext
    V_next = V_prev + dt * temp / tau
    if (V_next>theta): # 閾値θ超えてたら人為的に脱分極の電位にする
        return V_ex
    return V_next


# main loop
for t in range(1,num_t):
    V_list[t] = LIF(V_list[t-1], I)
    

# plot
plt.figure(dpi=100)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.xlabel("$t$",fontsize=20)
plt.ylabel("$V(t)$",fontsize=20)
plt.title('1N (LIF model)',loc='center',fontsize=25)
plt.plot(t_list, V_list, '-', color='steelblue', label="Legend")

シナプス

　上記ニューロンで発生したスパイク(脱分極)は、軸索を伝わり、シナプスを介して次のニューロンへと信号伝達がおきる。シナプス前後のニューロンを「プレ側」→「ポスト側」のように区別して呼ぶことにする。シナプスの正確な機構としては、「プレ側からシナプス小胞が放出され、ポスト側で受容体に結合し、膜電位が変化する」というメカニズムであるが、この辺は完全に無視して、プレ側で発火すると同時にポスト側のニューロンへ適当な外部電流を加えることで膜電位を変化させることにする (カレントベースモデル)。

ポスト側のニューロンへ加える電流を$I_\mathrm{syn}$として、$I_\mathrm{syn}$は「シナプス結合定数$\omega$」と「コンダクタンス$g_\mathrm{syn}$」の掛け算で計算することにする。

\begin{align}
 I_\mathrm{syn}(t) = \omega \ g_\mathrm{syn}(t) 
\end{align}

コンダクタンス$g_\mathrm{syn}$は、一度の発火($t=t_f$)で$\bar{g}_\mathrm{syn}$だけ発生し、これが時間経過と共にexpで減衰するとする。

\begin{align}
 g_\mathrm{syn}(t) = \bar{g}_\mathrm{syn} \sum_{t_f \in S(t_f)} e^{-\frac{t-t_f}{\tau}} \ \Theta(t-t_f)
\end{align}

→ 実際にシミュレーションする際には、過去の発火情報を全て保存する必要はなく、$g_\mathrm{syn}(t)$だけを保存し、毎stepごとに指数で減衰させていけばよい：

\begin{align}
 g_\mathrm{syn}(t+\Delta t) = g_\mathrm{syn}(t) e^{-\Delta t / \tau} + \bar{g}_\mathrm{syn} S(t)
\end{align}

シナプス結合定数$\omega$は、正の値であればEPSPを生じる興奮性シナプスを、負の値であればIPSPを生じる抑制性シナプスを表すとし、後に神経可塑性をシミュレーションする際には可変なものとして扱う。(機械学習におけるネットワークの結合定数に対応する。)

2ニューロン+シナプス

　実際に、最も簡単なケースとして、相互にシナプスで繋がっている2ニューロンの系をシミュレーションしてみる。シナプス結合定数$\omega$が正と負の2つの場合について以下に示す。

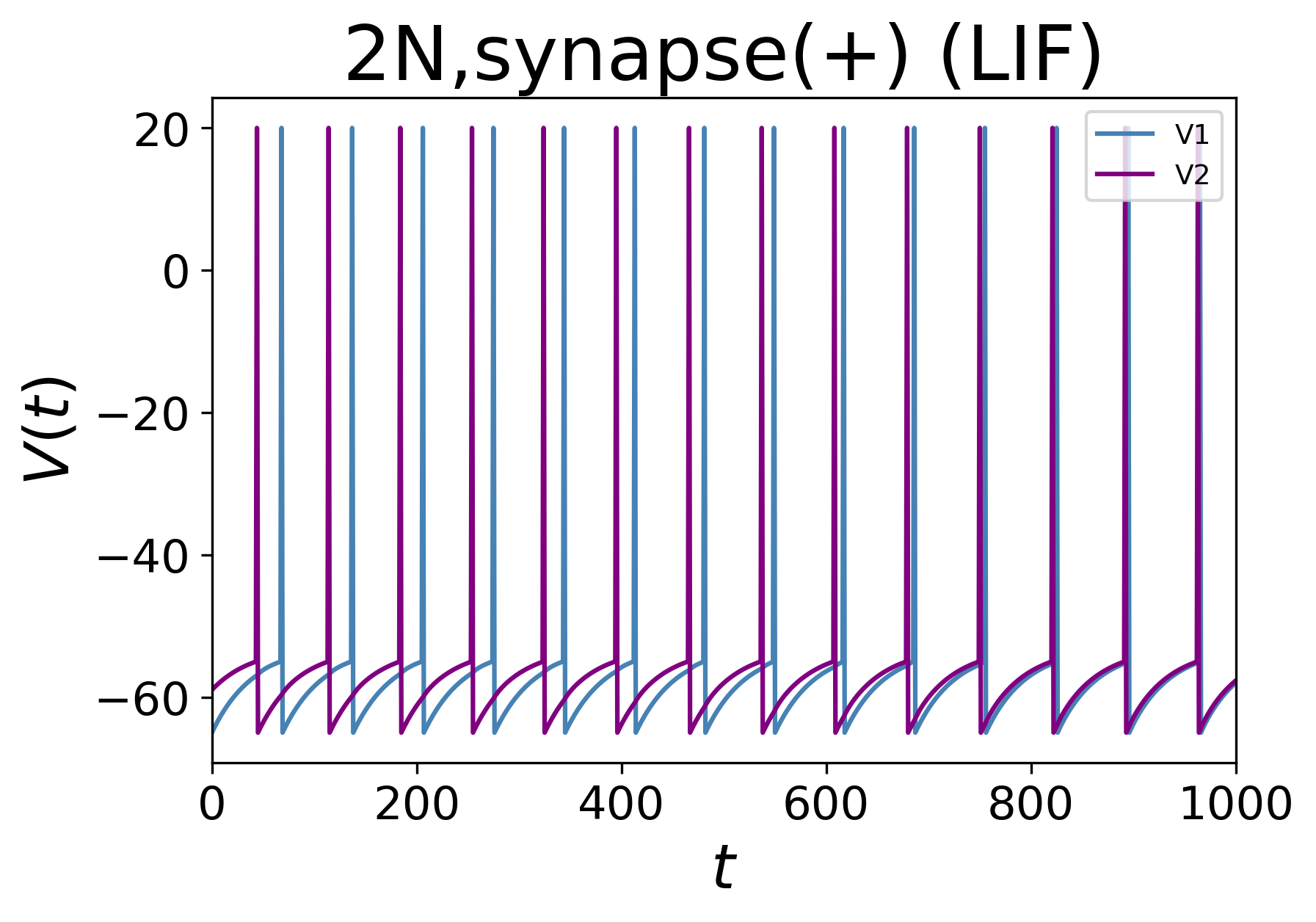
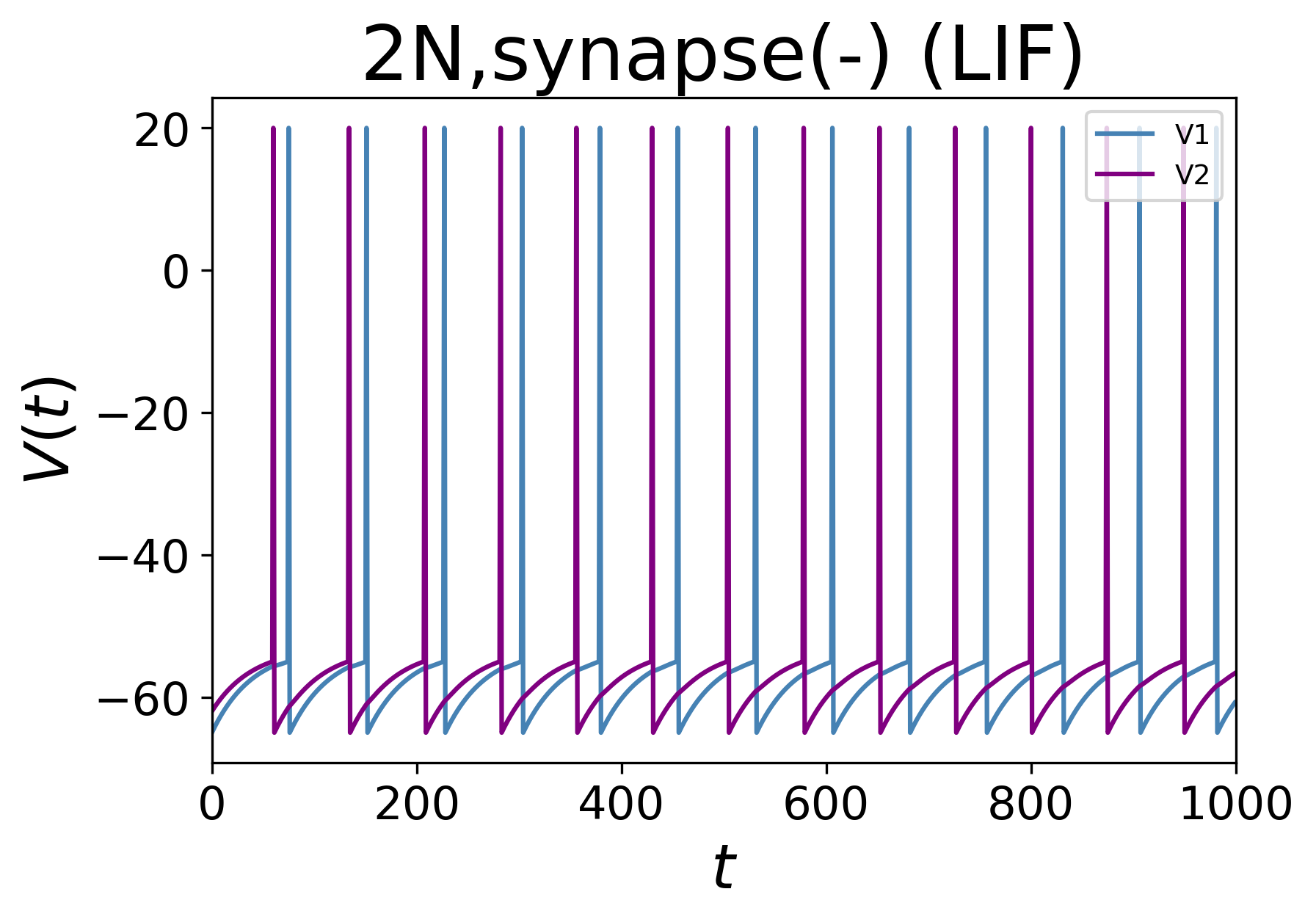
結合定数が正の場合、2ニューロンは徐々に波形が同期していき、逆に負の場合には波形の位相が反対に揃う様子がわかる。

実装例 (Python)

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

T = 1000 # ms
dt = 1   # ms
num_t = int(T/dt) # ms
# 神経細胞
R = 1  # MΩ
I = 12 # nA
V_eq = -65.0  # mV
V_ex = 20.0   # mV
theta = -55.0 # mV
tau = 40 # ms
# シナプス
g_syn = 1
tau_syn = 5 # ms
omega_syn = +2.0 # シナプス結合定数 (+2.0 or -2.0)


class Syn:
    
    def __init__(self):
        self.V = V_eq
        self.Sum = 0
        
    def LIF(self, i_ext):
        if (self.V>theta): # 前ステップで既に閾値θ超えてたら人為的にリセット
            return V_eq
        temp = - (self.V - V_eq) + R*i_ext
        V_next = self.V + dt * temp / tau
        if (V_next>theta): # 閾値θ超えてたら人為的に脱分極の電位にする
            return V_ex
        return V_next
        

t_list = np.array([t*dt for t in range(num_t)])
V1_list = np.zeros(num_t)
V2_list = np.zeros(num_t)


# main
x1 = Syn()
x2 = Syn()
x2.V = -59 # 少しズラす (-59 or -62)
V1_list[0] = x1.V
V2_list[0] = x2.V

for t in range(1,num_t):
    # シナプス電流
    x1.Sum = np.exp(-dt/tau_syn)*x1.Sum + omega_syn*(x2.V>theta)
    x2.Sum = np.exp(-dt/tau_syn)*x2.Sum + omega_syn*(x1.V>theta) 
    # 膜電位V更新
    x1.V = x1.LIF(I + g_syn*x1.Sum)
    x2.V = x2.LIF(I + g_syn*x2.Sum)
    V1_list[t] = x1.V
    V2_list[t] = x2.V
    # print(x.V)

# plot
plt.figure(dpi=100)
plt.xlim(0,T)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.xlabel("$t$",fontsize=20)
plt.ylabel("$V(t)$",fontsize=20)
plt.title('2N,synapse(+) (LIF)',loc='center',fontsize=25)
plt.plot(t_list, V1_list, '-', color='steelblue', label="V1")
plt.plot(t_list, V2_list, '-', color='purple', label="V2")
plt.legend(fontsize=9,loc="upper right")

一次視覚野の眼優位カラム

　ここでは、ヒトの脳で観察される特徴的な構造である「眼優位カラム」を神経回路シミュレーションによって再現してみる。一般に、眼から入力された視覚情報は、視神経を介して「一次視覚野」(大脳皮質の後頭部領域)へと伝えられる。この一次視覚野の細胞達は、右目からの入力に特に反応するものと左目に特に反応するものの2種類に役割が分かれていることが知られている。この2種類の細胞群はランダムに散在するのではなく塊状に連なって存在し、このような構造を眼優位カラムと呼ぶ (下図：左は実際の組織図、右はシミュレーション結果)。眼優位カラムは生まれつき持っている構造でなく、生後(2~8週間程度の間)に受ける外界の刺激に応じて自己組織化的に形成されるパターンであり、相分離現象において見られた現象とメカニズムは同じである。実際、産まれてすぐ単眼遮蔽すると、刺激が来ない方の眼からの入力に反応する細胞群が形成されずに片眼失明する (参考論文)。

問題設定

　シミュレーションするモデルの設定としては以下のようになる。

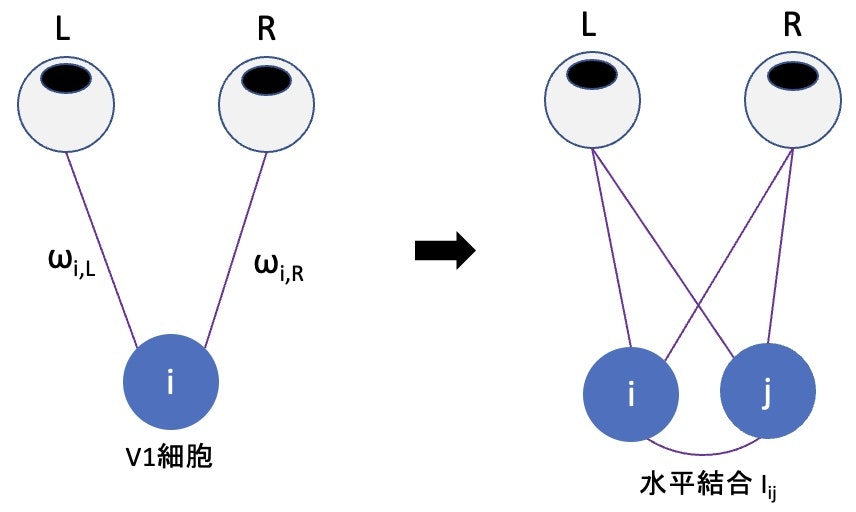
1. 2次元平面で格子状に一次視覚野(V1)細胞が並んでいるとして、V1細胞にそれぞれ両眼からのシグナルが入力される。両眼ともポアソン過程的に、一定の確率でランダム発火するとする。
2. あるV1細胞$(i)$と両眼$(L,R)$との間のシナプス結合の強さを$\omega_\mathrm{i,L}, \omega_\mathrm{i,R}$として、「$\omega_\mathrm{i,L} - \omega_\mathrm{i,R}$」が片眼優位性を示す指標となる(上図の左)。
3. シナプス結合は、ヘブ則に従いその結合強さが変化する。ここでは簡単なモデルとして、発火タイミング依存可塑性(STDP) を採用する。
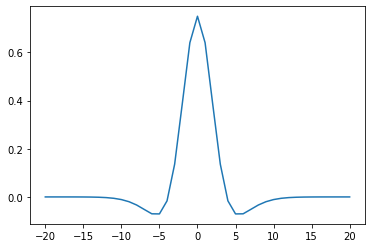
4. これだけでは、各V1細胞はバラバラに片眼優位性を獲得するのみである(下図の左のようになる)。そこで、近隣のV1細胞同士での相互作用(水平結合)を設定する。ごく近傍では強め合い、ある程度離れると弱め合うような、メキシカンハット型の水平結合を持つとした(上図の右)。
5. まとめると、1つのV1細胞には、「両眼からのランダムな発火シグナル$I_\mathrm{aff}$」と「他のV1細胞からの発火シグナル$I_\mathrm{lat}$」が外部電流として入力され、V1細胞が眼より遅れて発火すると結合定数が増大し早いと減少する(STDP則)とする：

\begin{eqnarray}
 \omega_{i,L} (t+\Delta t) = \omega_{i,L} (t) + A_+ x_L(t) S_i(t) + (-A_-)y_i(t)S_L(t)
\end{eqnarray} 

この式は、V1細胞$(i)$が発火した場合$S_i(t)=1$、それ以前に眼$(L)$が発火していれば定数$A_+$分だけ結合定数は増加し、逆であれば定数$(-A_-)$分だけ減少するということを表す。

数値計算

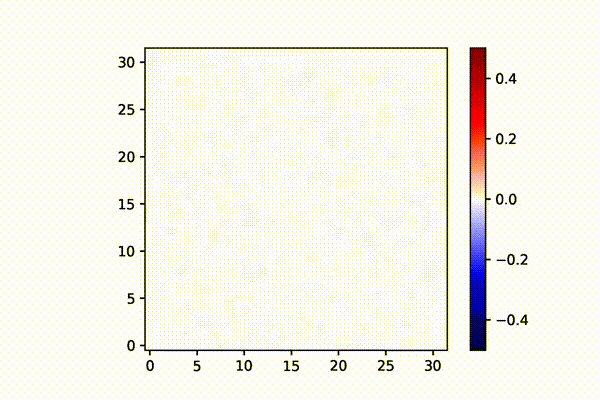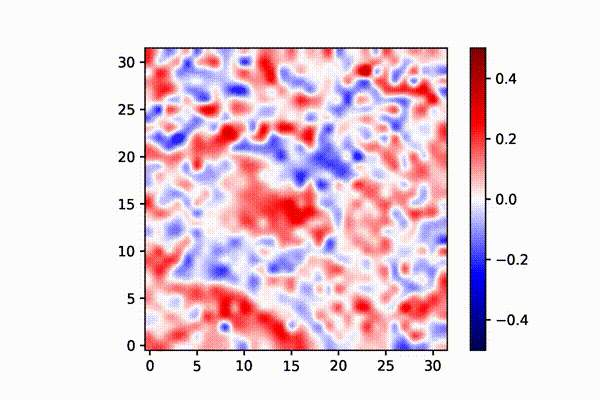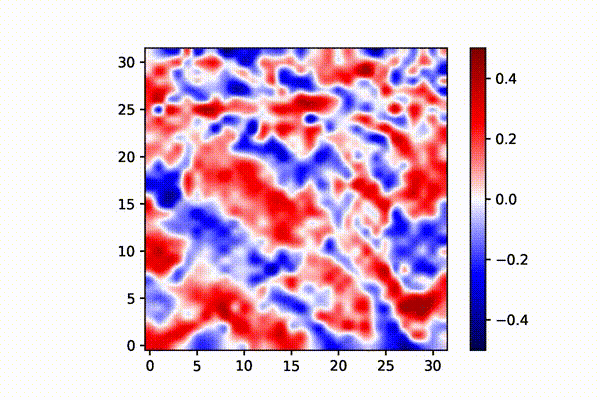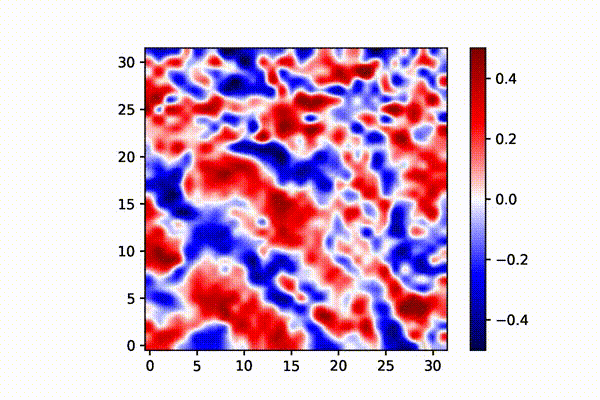
実際にシミュレーションした結果は下図のようになる。
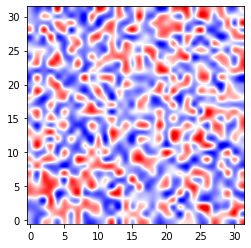
(左) 水平結合が0とすると、V1細胞はバラバラに活動し、1×1マス程度の構造しか形成しない
(中) 水平結合がある場合は、相互作用によって大きな島や縞状の構造が形成される。これが眼優位カラムである。
(右) 単眼遮蔽(右目からの入力頻度を1/10)した場合、片側の眼に優位なV1細胞が増えることが確認された。

実装例 (Python)

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import time

# 時刻t
T = 2000 # ms
dt = 1   # ms
num_t = int(T/dt) + 1
t_list = np.array([t*dt for t in range(num_t)])
tau_syn  = 5.0 # ms
tau_STDP = 10.0 # ms

# 神経細胞
R = 1  # MΩ
V_eq = -49.0  # mV (平衡電位が閾値より上、なぜ？ 公式コードではこうなっていた)
V_reset = -60 # mV
V_ex = 20.0   # mV
theta = -50.0 # mV
tau = 20 # ms

# 神経細胞の数 2次元平面 (num_nx × num_ny 個)
num_nx = 32
num_ny = 32
num_N = num_nx*num_ny
A_plus  = 0.02
A_minus = 0.02

# 視細胞からのシグナル
s_eye_L = [0 for t in range(num_t)]
s_eye_R = [0 for t in range(num_t)]
eye_L_STDP = [0.0 for t in range(num_t)]
eye_R_STDP = [0.0 for t in range(num_t)]
for t in range(num_t): # 10回に1回ランダムで発火
    if(np.random.rand() <= 0.1):
        s_eye_L[t] = 1
    if(np.random.rand() <= 0.01):
        s_eye_R[t] = 1
eye_L_STDP[0] = s_eye_L[0]
eye_R_STDP[0] = s_eye_R[0]
for t in range(1,num_t):      
    eye_L_STDP[t] = eye_L_STDP[t-1]*np.exp(-dt/tau_STDP) + s_eye_L[t]
    eye_R_STDP[t] = eye_R_STDP[t-1]*np.exp(-dt/tau_STDP) + s_eye_R[t]

# シナプス電流
g_aff = 2.0
g_lat = 4.0 # 0にすればただの2ニューロン+1シナプスモデル

# 水平結合 I(i,j) = I_ij_list[|i-j|] (*周期的境界条件)
sig_1 = 4.0
sig_2 = 16.0
k1 = 1.0
k2 = sig_1/sig_2
norm_coeff = 1.0 / ( k1*np.sqrt(2.0*sig_1*np.pi) - k2*np.sqrt(2.0*sig_2*np.pi) )

def Calc_I_ij(dif):
    return norm_coeff * ( k1*np.exp(-dif/(2.0*sig_1)) + (-k2)*np.exp(-dif/(2.0*sig_2)) )

I_ij_list = np.zeros((num_nx,num_ny))

for i in range(num_nx):
    for j in range(num_ny):            
        d2 = i*i + j*j
        I_ij_list[i][j] = Calc_I_ij(d2)

S_list = np.zeros((num_nx,num_ny))

# 神経細胞のクラスを定義
class Neuron:
    
    def __init__(self,i,j):
        self.i = i
        self.j = j
        self.V = V_reset + 10.0*np.random.rand()
        self.S = 0 # 発火したかどうか
        self.STDP = 0.0 # トレース x_i,y_i
        self.w_L = 0.49 + 0.01*np.random.rand() # ω_{i,L}
        self.w_R = 0.49 + 0.01*np.random.rand() # ω_{i,R}
        self.I_ext = 0.0 # 外部電流 合計(aff+lat)
        self.I_aff = 0.0 # 外部電流 aff
        self.I_lat = 0.0 # 外部電流 lat
        
        self.dif_list = np.zeros((num_nx,num_ny))
        for k in range(num_nx): 
            for l in range(num_ny):
                self.dif_list[k][l] = I_ij_list[np.abs((self.i-k))][np.abs((self.j-l))]
    
    def Calc_i(self, time):
        # aff
        self.I_aff *= np.exp(-dt/tau_syn)
        self.I_aff += self.w_L*s_eye_L[time] + self.w_R*s_eye_R[time]  
        
        # lat
        self.I_lat *= np.exp(-dt/tau_syn)        
        temp = S_list
        temp[self.i][self.j] = 0.0
        lat_list = self.dif_list*temp # 計算量O(N^2) for文遅いので numpyで高速化
        self.I_lat += np.sum(lat_list)
    
        # ext
        self.I_ext = self.I_aff*g_aff + self.I_lat*g_lat
        return 0
        
    def LIF(self):  # 膜電位V(t)を1step更新
        self.S = 0
        temp = - (self.V - V_eq) + R*self.I_ext # 膜電位は、(V_eq + RI)に向かって、τ(20ms)ぐらいで緩和していく時間発展
        self.V += + dt * temp / tau
        if (self.V>theta): 
            self.V = V_reset  # 閾値θ超えてたら人為的に脱分極の電位にする
            self.S = 1     # この時刻で発火したフラグ
        return 0
    
    def Update_Trace(self): # トレースを更新
        self.STDP = self.STDP*np.exp(-dt/tau_STDP) + self.S
        return 0
        
    def Update_Omega(self,time): # 結合定数ωを更新
        # 自分が発火した時(S=1)に、eyeのこれまでのSTDPトレースを加える
        # eyeが発火した時(s_eye_L=1)に、SのこれまでのSTDPトレースを加える
        self.w_L += A_plus*eye_L_STDP[time]*self.S + (-A_minus)*self.STDP*s_eye_L[time]
        self.w_R += A_plus*eye_R_STDP[time]*self.S + (-A_minus)*self.STDP*s_eye_R[time]
        self.w_L = max(0.0, self.w_L) # 負の値にはしない
        self.w_R = max(0.0, self.w_R) # 負の値にはしない
        self.w_L = min(1.0, self.w_L) # 1.0は超えない
        self.w_R = min(1.0, self.w_R) # 1.0は超えない
        return 0
       
    

# main
N_list = [[Neuron(i,j) for j in range(num_ny)] for i in range(num_nx)]
#print(N_list[5][5].j)
Data_list1 = np.array([ [ [0.0 for j in range(num_ny)] for i in range(num_nx)]  for t in range(num_t)])

for t in range(2001):
    for i in range(num_nx):
        for j in range(num_ny):
            S_list[i][j] = N_list[i][j].S
    for i in range(num_nx):
        for j in range(num_ny):
            N_list[i][j].Calc_i(t)
    for i in range(num_nx):
        for j in range(num_ny):
            N_list[i][j].LIF()
    for i in range(num_nx):
        for j in range(num_ny):
            N_list[i][j].Update_Trace()
    for i in range(num_nx):
        for j in range(num_ny):
            N_list[i][j].Update_Omega(t)
    
    if (t%50==0):
        for i in range(num_nx):
            for j in range(num_ny):
                Data_list1[t][i][j] = N_list[i][j].w_L - N_list[i][j].w_R
        data = Data_list1[t]
        fig, ax = plt.subplots()
        im = ax.imshow(data, cmap='seismic', vmin=-0.5, vmax=0.5, origin='lower', interpolation='spline16') # 補完入れないとそれっぽく見えない
        plt.colorbar(im)
        plt.show()