生物物理学 まとめ&実装

　「生物物理学 (鳥谷部祥一 著)」を読みながら、個人的に面白かった部分を抜粋して、まとめ&実装&コメントしている。公式の実装例(Github)も一部参考にしながら実装した。徐々に数式要素が強くなり、後半は物理系の大学院生向けかも。数式的な部分は、より詳細な「非平衡系の物理学 (太田隆夫 著)」を適宜参照した。

アロステリック効果 (第3章)

　代表的なヘモグロビン(wikipedia)について扱う。ヘモグロビンは、血液中で酸素分子を運搬するタンパク質の一種である。1つのヘモグロビンには、4つの酸素分子結合サイトが存在する。生理的条件下で、酸素結合曲線(酸素が結合しているサイト数 vs 酸素分圧)はシグモイド状のカーブを描く(下図、本より引用)。これは酸素分圧の高い肺においては多量の酸素と結合して吸着し、酸素分圧の低い末梢組織では酸素親和性が低くなり放出することで、肺から全身へ酸素を運搬する役割を果たしている。単純な比例関係の場合に比べると効率的に酸素を運搬できることがわかる。

もし、酸素分子が4つの結合サイト同士が相互作用せず独立であれば、直感的に酸素結合曲線はほぼ直線状になるはずである。実際には、酸素分子が既にどこかのサイトに結合しているヘモグロビンにおいては、他の未結合サイトの結合能が高まる性質があり、結果的に急峻な立ち上がりカーブを持つシグモイド曲線となるらしい。これを「アロステリック効果」と呼び、生体内での酵素において普遍的に見られる。

　今回は「ポーリングモデル」を実装してアロステリック効果を再現する。酸素が結合可能な4サイトを$i=1\sim4$と番号を付けて、各サイトに酸素分子が結合している状態(1)としてない状態(0)を集合$\lbrace \sigma_i \rbrace$で表す。$\lbrace \sigma_i \rbrace = \lbrace 0,0,0,0 \rbrace, \lbrace 0,0,0,1 \rbrace... $ のように16パターン存在することがわかる。結合サイト数を$N(=0\sim4)$、また隣り合うサイト同士では相互作用$J(<0)$により安定化するとして、その数を$M(={}_4 C_N)$とする。
(結合サイト数が半分ぐらいの場合の状態数が最も多く、これでエントロピー効果を考慮していることになる。また相互作用$J=0$で直線状、$J$を大きくしていくとシグモイド状に変化することを再現したい。)

$N$	0	1	2	3	4
状態数	1	4	6	4	1
$M$	0	0	1	2	4
$E$	$0$	$(\epsilon-\mu)$	$2(\epsilon-\mu)+J$	$3(\epsilon-\mu)+2J$	$4(\epsilon-\mu)+4J$

酸素分子は、「血液中では水側に解ける」or「ヘモグロビンに結合する」の2状態のどちらかを取ることになる。2状態の持つそれぞれの自由エネルギーを表現するために、酸素分子が水に溶けてる場合のエネルギーを表す化学ポテンシャル$\mu=k_B T \ln(P_{O_2} / P_0)$、またヘモグロビンとの結合エネルギー$\epsilon<0$を定義すると、全エネルギー$E$は

  E(\lbrace \sigma_i \rbrace) = (\epsilon-\mu)N + JM.

各$N$の際に$E$がどうなるかを上表に併記している。統計力学によると、各状態はエネルギーが低いほど実現確率が高いというBoltzman分布$e^{-\beta E}$に従う。

Boltzman分布と状態数をかけ合わせて定義される、分配関数$Z$は、

\begin{align}
 Z &= \sum_{\lbrace \sigma_i \rbrace} e^{-\beta E(\lbrace \sigma_i \rbrace)} \\
 &= \sum e^{-\beta [(\epsilon-\mu)N+JM] } \\
 &= 1 + 4e^{-\beta(\epsilon-\mu)} + 6e^{-\beta[2(\epsilon-\mu)+J]} + 4e^{-\beta[3(\epsilon-\mu)+2J]} + e^{-\beta[4(\epsilon-\mu)+4J]}
\end{align}

求めたかった結合サイト数の期待値$\langle N \rangle$は、分配関数と似た式を使って表される。(本の演習問題の解答間違い？)

\begin{align}
 \langle N \rangle &= \frac{\sum N e^{-\beta E}}{\sum e^{-\beta E}} \\
 &= \frac{4e^{-\beta(\epsilon-\mu)} + 12e^{-2\beta(\epsilon-\mu)-\beta J} + 12e^{-3\beta(\epsilon-\mu)-2\beta J} + 4e^{-4\beta(\epsilon-\mu)- 4\beta J}}{Z} 
\end{align}

実際に$\langle N \rangle$を計算してプロットしたのが下図となる。相互作用$J$の絶対値を0から始めて大きくしていくと、直線状からシグモイド状へと変化していくことがわかる。

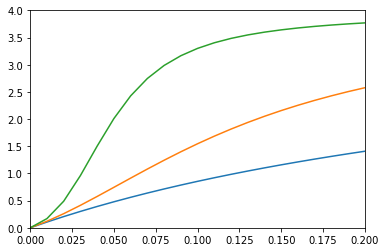
実装例

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# 初期値
b = 1 # beta
e = -1 # epsilon

def Func_Z(mu, J):
    temp = np.array([0.0]*5)
    temp[0] = 1
    temp[1] = 4*np.exp(-b*(e-mu))
    temp[2] = 6*np.exp(-b*(2*(e-mu)+J))
    temp[3] = 4*np.exp(-b*(3*(e-mu)+2*J))
    temp[4] = 1*np.exp(-b*(4*(e-mu)+4*J))
    return np.sum(temp)

def Func_N(mu, J):
    temp = np.array([0.0]*5)
    temp[0] = 0
    temp[1] = 4*np.exp(-b*(e-mu))
    temp[2] = 12*np.exp(-b*(2*(e-mu)+J))
    temp[3] = 12*np.exp(-b*(3*(e-mu)+2*J))
    temp[4] = 4*np.exp(-b*(4*(e-mu)+4*J))
    return np.sum(temp)/Func_Z(mu,J)

p_list = np.array([0.01*i for i in range(101)])
N_list0 = np.array([Func_N(1.0/b*np.log(p_list[i]),-0.0) for i in range(101)]) # J = 0
N_list1 = np.array([Func_N(1.0/b*np.log(p_list[i]),-1.0) for i in range(101)]) # J = -1
N_list2 = np.array([Func_N(1.0/b*np.log(p_list[i]),-2.0) for i in range(101)]) # J = -2

plt.xlim(0.0,0.2)
plt.ylim(0.0,4.0)
plt.plot(p_list, N_list0)
plt.plot(p_list, N_list1)
plt.plot(p_list, N_list2)
plt.show()

コメント

1. アロステリック効果は、医学書では結合により酵素の立体構造が変わることで起こると書いている。これが正しいのであれば、結合サイト間の相互作用というモデル化はあまり適切でないように思える。
2. 立体構造変化による結合能の変化は、第一原理計算で頑張れば再現できそう。これがポーリングモデルの仮定とどの一致しているのか気になるところ
3. 前記事にした、Hodgkin-Huxleyモデルにおいてはイオンチャネルを構成する4量体がそれぞれ独立であるとして扱っていたが、アロステリックな効果は無いのか？
4. 相互作用モデルが2量体や8量体などの場合にどれくらい性質が変わるのか、 ヘモグロビンが4量体である必然性はあったのだろうか？そういえば生体内のタンパク質で、2量体~4量体はよく出てくるが、それ以上のサブユニットで構成されるものは見たことないかも。(サブユニット数を増やしすぎると、一つでも合成失敗したら全体がダメになるリスクがありそう。実際3量体のコラーゲン分子では片方のアレル変異で重篤な疾患を引き起こす遺伝病がある：栄養障害型の表皮水疱症)

相分離生物学 (第12章)

　真核生物の細胞内には、核や小胞体などの膜を持つ細胞内小器官(オルガネラ)が多数存在しており、これらは細胞質を分画化することで基質濃度を上昇させ、特定の代謝や情報伝達を効率的かつ混線を防ぎながら反応を進めるという役割がある。しかし、これだけでは細胞質内の多段階酵素反応は説明できない(不安定な中間体が次の酵素に運良く捕まる確率は相当低い)とされており、実際細胞内には「膜のないオルガネラ」が形成され利用されていることが近年理解され始めている。
　膜のないオルガネラは、液-液相分離と呼ばれる細胞質内の熱力学的な相分離によって形成される「ドロップレット」であり、通常のオルガネラと比べると小さく不安定だが、逆に動的に生成/消滅する小規模な反応区画として積極的に利用されている。
　以下では、相分離を再現する数理モデルについて解説した後、現在わかりつつある相分離生物学の研究について述べる (後者は主に「相分離生物学 (白木賢太郎 著)」を参照している)。

相分離

　溶液中に複数種の粒子(簡単にAとBの2種類とする)が存在する場合を考える。直感的には、粒子間に相互作用が全くなければ溶液中で均一に混合され、同一粒子間に引力相互作用があれば分離してそれぞれが集団を作りそう(= 相分離)である。これは熱による拡散(エントロピー$S$増大)と引力による安定化(ポテンシャルエネルギー$U$減少)がせめぎあっていて、それが釣り合う状態(自由エネルギー $F=U-TS$ が極小)に落ち着くものと熱力学的には理解できる。粒子比に応じた自由エネルギー変化の模式図(下図、本§13.5より引用)を参考にすると、相分離状態とは、自由エネルギー図において極小点が複数存在し、それぞれが別の相を形成し安定化するのだとわかる。

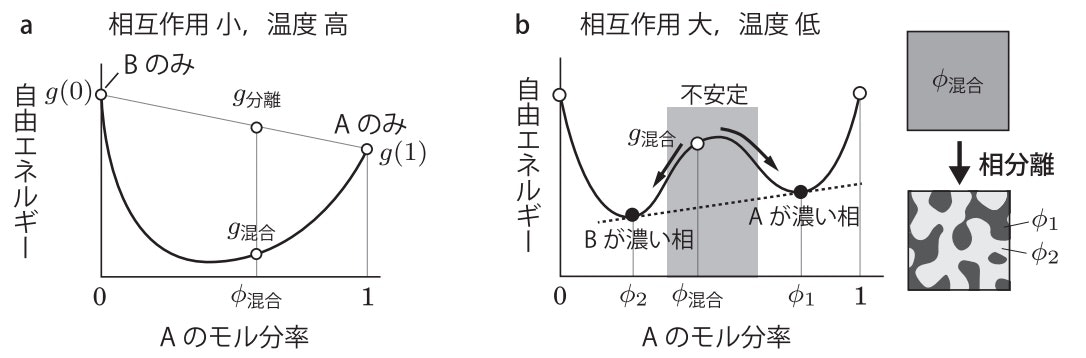
　また、別の準安定状態である極大点が不安定領域にある場合は、容易に相分離が起きて全体が繋がったような共連結型パターンを示し、これをスピノーダル分解と呼ぶ。もし極大点が不安定領域外にある場合、自由エネルギーが高い相を形成するには極大点の山を超える(= 核生成に対応？)が必要であり、粒子状の領域が複数形成されるようなドロップレット型のパターンを示す。

　実際、粒子の熱拡散と引力相互作用をモデル化した次のセルオートマトンでは、相分離状態が形成されることが確認できる (本のコードを一部改変してアニメーション化した)。(左)相互作用が0の場合、粒子はランダムに拡散し全体として均一な濃度となる。相互作用を設定すると、右2つのgif画像のように相分離が起きた：粒子数が少ない場合はドロップレット型(真ん中)、多い場合にスピノーダル分解(右)となる。特に、ドロップレット型では、粒子状領域が動的に生成/消滅している様子が確認される、この現象は生体細胞内で積極的に利用されていることが近年わかって来た。

膜のないオルガネラ

・膜のないオルガネラ
細胞内において、脂質膜なしでタンパク質やRNAなどが液-液相分離により凝集した領域のことを指し、
　1. 核小体：核内にあり、最大サイズのドロプレットを形成、リボソーム合成が行われる
　2. カハール小体：増殖細胞の核内にあり、核小体と結合している
　3. ストレス顆粒：環境ストレスに応答して形成され、ストレスがなくなるまで翻訳を抑制
などがある。

・液-液相分離
タンパク質やRNAが電荷相互作用により集まり、球状のドロップレットとして相分離する現象である。ドロップレットは不安定な構造のため温度やpHで動的に変化する。タンパク質が壊れていたり、強く結合しすぎると凝集体(アミロイド)を形成し、種々の神経変性疾患などを引き起こすことがわかっている。他の細胞への感染能を持つものがプリオンである。

・ドロップレット

1. 反応促進：形成されたドロップレットは、自身に親和性の高い分子を取込み、低い分子を排斥しながら成長する。これにより基質の濃縮が行われ、効率的な反応の場としての役割を果たす。例えば、DNAは共通の配列を認識して集まってくる転写因子やエンハンサーとドロプレットを形成することで、特定の遺伝子領域からの転写活性を上昇させているようである。
2. エピジェネティック制御：この親和性は化学修飾によって変化するので、反応や転写をコントロールする新たなエピジェネティック制御の機構としても着目されている。
3. ストレス応答：酵母では、飢餓状態でpHが低下するとドロップレットが形成され、タンパク質の新たな翻訳が行われないよう耐える、ような仕組みが観測されている。また、翻訳直後の未熟なタンパク質がきちんとフォールディングされるまで、外界から保護するドロップレットを形成するような「相分離シャペロン」も確認されている。一方、長時間ドロップレット状態にあるとタンパク質同士が強く結合して凝集体を形成する場合もあり、危険なアミロイドやプリオンのタンパク質が生物の進化過程で保存されてきたのは、本来ドロップレット形成という重要な役割を持つものだからであると推測されている。

ブラウン運動 (第6章)

　生体内のタンパク質や分子は、絶えず周りの水分子などから無数の衝突を受けゆらぎ続け、溶液中を拡散していく。このような熱ゆらぎによる粒子のブラウン運動(wikipedia)をモデル化して扱えるようにしたい。直感的にわかりやすいランダムウォークから出発して、徐々に複雑化させて種々の方程式や定理を導出する。

0. 熱ゆらぎ

　熱ゆらぎは、何らかの確率分布に従って周囲環境の粒子がランダムに多数衝突することで起きる。その分布自体を知ることは出来ないが、方向がバラバラであるから、平均を取れば0になる。また、マクロに見ると衝突された物体を動かすのは、その平均からのズレであり、「中心極限定理」から、このズレ動かす力つまり誤差の分布は正規分布とみなせるはず。
以下、熱ゆらぎを「平均0の正規分布に従うノイズ」としてモデル化する。

1. ランダムウォーク

　最も簡単化して、ある1粒子が1次元$x$軸上を、離散化された空間/時間で移動する場合を考える。つまり、粒子は時間$\tau$ごとに、確率$p$で$+d$・確率$p$で$-d$・確率$1-2p$で$0$の距離を移動するとしてモデル化する。粒子の位置は1ステップごとに$x_0 \rightarrow x_1 ... \rightarrow x_n$と移動するとして、

$1$ステップの過程を考えると
・平均位置は、

 \langle \Delta x \rangle = 0.

・分散は、

 \langle (\Delta x)^2 \rangle = pd^2 + pd^2 + (1-2p)\times0^2 = 2pd^2.

$n$ステップ後の
・平均位置は、

 \langle (x_n-x_0) \rangle = n\langle \Delta x \rangle = 0.

・分散は、

\begin{align}
 \langle (x_n-x_0)^2 \rangle &= \langle \left[ (x_n-x_{n-1}) + (x_{n-1}-x_{n-2}) + ... + (x_1 - x_0) \right]^2 \rangle \\
 &= \langle (x_n-x_{n-1})^2 \rangle + \langle (x_{n-1}-x_{n-2})^2 \rangle + ... + \langle (x_{1}-x_{0})^2 \rangle \\
 &+ 2\langle(x_n-x_{n-1})(x_{n-1}-x_{n-2})\rangle + 2\langle(x_{n-1}-x_{n-2})(x_{n-2}-x_{n-3})\rangle + ... \\
 &= n\langle (\Delta x)^2 \rangle \\
 &= 2npd^2.
\end{align}

時間を$t \equiv n\tau$と定義し直し、単位時間あたりの遷移率を$\omega \equiv p/\tau$、拡散係数$D \equiv \omega d^2$として、

\begin{align}
 \langle \left[ x(t)-x(0) \right]^2 \rangle &= 2Dt
\end{align}

拡散係数$D$は、遷移確率$\omega$に比例し、移動距離$d$の2乗に比例する。つまり拡散しやすさに対応している係数。
また、分散の式から、時間$t$の$\sqrt t$に比例する形で粒子は元いた位置からの距離分布の裾野が広がっていく。これは、通常の等速運動(時間$t$に対して移動距離の分散は2乗、距離分布は比例する形)と異なっている。

マスター方程式
　ランダムウォークを、時間連続的な式に書き換える。
粒子が時刻$t$にセル$k$にいる確率$P_k(t)$として、遷移確率$\omega$で隣のセルに移動するとすると、

\frac{dP_k(t)}{dt} = \omega P_{k-1}(t) + \omega P_{k+1}(t) - 2\omega P_k(t)

右辺第1と2項が流入、第3項が流出を表す。

拡散方程式
　さらに、空間方向にも連続化することで拡散方程式が得られる。$P_k(t)$を粒子密度$\rho(x,t)$で$P_k(t)\equiv \int_{kd}^{(k+1)d} \rho(x,t)dx$と表す。格子サイズ$d$が十分に小さいとして、$P_k(t)\sim \rho(kd,t)d$のように近似し、マスター方程式に代入すると、

\begin{align}
 \frac{\partial \rho(x,t)}{\partial t} &= \omega \rho(x-d,t) + \omega \rho(x+d,t) - 2\omega \rho(x,t) \\
 &= \omega [\rho(x-d,t)-\rho(x,t)] + \omega[\rho(x+d,t)-\rho(x,t)] \\
&= D \frac{\partial^2 \rho(x,t)}{\partial x^2}
\end{align}

・移流項
　位置$x$を通過する単位時間当たりの粒子数(正の方向を＋,負の方向を-でカウントする)を移流$J(x)$とすると、粒子が生成消滅しないならば、粒子密度の時間変化が移流の空間変化と等しくなるので、$[J(x+dx,t)-J(x,t)]dt = -[\rho(x,t+dt)-\rho(x,t)]dx$、極限を取ると

\begin{align}
 \frac{\partial \rho}{\partial t} = - \frac{\partial J}{\partial x}
\end{align}

拡散方程式と比較して、

\begin{align}
 J(x) = - D \frac{\partial \rho}{\partial x}
\end{align}

・移流拡散方程式
　一定の外力が加わる下での拡散方程式を考える。拡散項に加えて一定の平均速度$u$で動く移流項を加えればよい。

\begin{align}
 \frac{\partial \rho(x,t)}{\partial t} =-u \frac{\partial \rho(x,t)}{\partial x} +  D \frac{\partial^2 \rho(x,t)}{\partial x^2} 
\end{align}

アインシュタインの関係式
　上の移流拡散方程式は、平衡状態($\partial \rho(x,t) / \partial t = 0$)を考えると、拡散項と移流項による流れが釣り合って見かけ上の定常状態になっているはずである。教科書のように、重力$f$に従って床に落ちていく粒子群を考えると、

・移流拡散方程式
左辺が0なので、微分方程式を解くと

\begin{align}
 u \frac{\partial \rho(x,t)}{\partial x} &=  D \frac{\partial^2 \rho(x,t)}{\partial x^2}  \\
 u \rho &= D \frac{\partial \rho}{\partial x} \\
 \rho_\mathrm{eq}(x) &= A e^{\frac{u}{D}x}
\end{align}

・ボルツマン分布
平衡状態であるから、粒子の分布位置は重力の位置エネルギーに依存したBoltzmann分布となるので、

\begin{align}
 \rho_\mathrm{eq}(x) &= \frac{1}{Z} e^{- \frac{f}{k_B T} x}
\end{align}

→ 上2式のAとZは規格化定数であり、指数を比較すると

\begin{align}
 D &= \mu k_B T \\
\end{align}

易動度$\mu \equiv - \frac{u}{f}$は、力$f$に対して速さ$u$で動く、つまり粒子群の動き易さ(=応答)を表す。上式は、平衡状態において、応答$\mu$とゆらぎ$D$の大きさが比例関係にあることを示す、「揺動散逸関係」の一種である。これは、平衡状態近傍で熱ゆらぎ系の応答が外力に比例する「線形応答領域」において、普遍的に成り立つ関係である。

2. ランジュバン方程式

　ここまではランダムウォークから出発して発展させて来たが、根本となる粒子の運動の駆動力を遷移率$\omega$という物理的実体がよくわからない謎概念をベースにしていたことになる。もう少し物理っぽく、熱ゆらぎの駆動力を確率分布を持つ実際の力として表現し、運動方程式を作ってみる。

厳密に運動方程式を立てるのであれば、アボガドロ数個ある溶媒分子と粒子の衝突について全て連立することになるが、あまり現実的ではない。もう少し粗視化して、粒子が止まっているときに衝突してくる揺動力$\xi(t)$、粒子が移動しているときに溶媒分子が邪魔してくる効果を摩擦力的な感じ$-\gamma \dot{x}$で表現する。外力$f_\mathrm{ext}(x,t)$も考慮した運動方程式は、

\begin{align}
 m \ddot{x} &= f_\mathrm{ext}(x,t) + \xi(t) - \gamma \dot{x} \\
\end{align}

これを「ランジュバン方程式」と呼ぶ。ここで、熱揺動力と摩擦力は、共に熱ゆらぎに起因するものであり、平衡状態では両者に次の揺動散逸関係が成立する。

\begin{align}
 \langle \xi(t) \xi(s) \rangle &= 2\gamma k_B T \delta(t-s) \\
\end{align}

左辺は揺動力$\xi$の自己相関関数であり、右辺では$t=s$の時のみ有限の値(マルコフ過程なので)を取り、その大きさは摩擦力$\gamma$に比例することを表している。

揺動散逸関係の導出

「非平衡系の物理学(太田隆夫)」を参照にした。
マルコフ過程なので、

\begin{align}
 \langle \xi(t_1) \xi(t_2) \rangle &= 2M \delta(t_1-t_2) \\
\end{align}

のようなポアソン過程っぽい関係は成り立つはずで、後はこの$M$が摩擦力を含むことを示す。

・右辺のデルタ関数は、フーリエ変換的な感じの積分表記でも書けるのであった：

\begin{align}
 2M \delta(t_1-t_2) &= \frac{2M}{2\pi} \int e^{-i\omega(t_1-t_2)} d\omega  \\
\end{align}

・左辺の自己相関関数をフーリエ変換で表すと：

\begin{align}
 \langle \xi(t_1) \xi(t_2) \rangle 
 &= \frac{1}{(2\pi)^2} \int \langle \xi_{\omega_1} \xi_{\omega_2} \rangle e^{-i\omega_1 t_1 - i \omega_2 t_2} d\omega_1 d\omega_2
\end{align}

上2式が、あらゆる$t_1,t_2$で一致するためには、指数の肩の第一項が$\omega=\omega_1$、さらに第二項から$\omega_2=-\omega_1$でなければならない。これらを代入して、

\begin{align}
 \langle \xi(t_1) \xi(t_2) \rangle 
 &= \frac{1}{2\pi} \int \langle \xi_{\omega} \xi_{-\omega} \rangle e^{-i\omega (t_1-t_2)} d\omega
\end{align}

比較すると、

\begin{align}
  \langle \xi_{\omega} \xi_{-\omega} \rangle &= 2M
\end{align}

次に速度の相関関数$\langle v(t_1) v(t_2) \rangle$を計算する。運動方程式をフーリエ変換すると、

\begin{align}
 v_\omega &= \frac{\xi_\omega}{-i\omega m + \gamma} \\
 \langle v_\omega v_{-\omega} \rangle &= \frac{\langle \xi_\omega \xi_{-\omega} \rangle}{(\omega m)^2 + \gamma^2} = \frac{2M}{m^2} \frac{1}{\omega^2 + \kappa^2}\\
\end{align}

これを逆フーリエ変換して、

\begin{align}
 \langle v(t_1) v(t_2) \rangle &= \frac{2M}{m^2} \int \frac{1}{\omega^2 + \kappa^2} e^{i\omega(t_1-t_2)} d\omega \\
 &= \frac{M}{m\gamma} e^{-\kappa |t_1-t_2|}
\end{align}

(よく見ると時間の"差"の関数となっている。$t_1,t_2$を入れ替えても不変であることになるが、摩擦力を導入すると普通の運動方程式では時間対称性は破れるので不自然な感じがある。→ 今は平衡状態で熱ゆらぎにより揺れ動く速度$v$について考えている、摩擦力は揺動力とバランスした定常状態なので、時間対称性が維持されているのはそれほど不思議ではないのだ)

$t_1=t_2$とすると、

\begin{align}
 \langle v(t)^2 \rangle &= \frac{M}{m \gamma}
\end{align}

統計力学的な概念から、平衡状態では粒子の平均運動エネルギーは、$\frac{1}{2}m\langle v^2 \rangle = \frac{1}{2}k_B T$と書けるのであった(1次元空間で1粒子の自由度が1とした)ので、上式と比較すれば、

\begin{align}
 M = \gamma k_B T
\end{align}

3. フォッカー・プランク方程式

　ランジュバン方程式を闇雲にシミュレーションで何回も解いて粒子の確率分布を近似的に求めることも出来るが、粒子の存在位置を最初から確率分布として表して、確率分布の時間発展方程式を作ることが出来る。

一般的なガウンシアンノイズを含む確率微分方程式を考える：

\begin{align}
 \dot x = a(x) + b(x) R(t), \\
 \langle R(t)R(s) \rangle = c \delta(t-s)
\end{align}

$x(t)$を表す確率分布$P(x,t)$の時間発展方程式は、次のフォッカー・プランク方程式で書ける(導出は「非平衡系の物理学」§5.8)：

\begin{align}
 \frac{\partial P(x,t)}{\partial t} &= -\frac{\partial}{\partial x} [A(x)P(x,t)] + \frac{1}{2} \frac{\partial^2}{\partial x^2} [B(x)P(x,t)] \\
A(x) &\equiv a(x) + \frac{c}{2}\frac{\partial b(x)}{\partial x} b(x) \\
B(x) &\equiv c[b(x)]^2
\end{align}

つまり、最初の確率微分方程式の形に帰着できれば、後はフォッカー・プランク方程式をシミュレーションすることで確率分布を求めることが出来る。例えば、拡散方程式は$a(x)とb(x)$が定数の場合である。ランジュバン方程式も、熱力学ポテンシャルで書き換えた表式では、最初の確率微分方程式に帰着させることができる。

実際にシミュレーションした結果をWeb上で載せている方が居たので引用させてもらいます(kT@物理・化学 Yusuke Tominaga)：
場所1と2を$N$個の粒子がランダムに飛び移る確率過程を考えると、$A,B$を計算して次のような式になるらしい

\begin{align}
 \frac{\partial P(x,t)}{\partial t} = &- \frac{\partial}{\partial x} \left[ (0.2N-0.8x) \, P(x,t) \right] \\
&+ \frac{1}{2}\frac{\partial^2}{\partial x^2} \left[ (0.04N^2 + 0.16N - 0.32Nx + 0.64x^2 + 0.08x) \, P(x,t) \right]
\end{align}

初期条件は$N=400,P(x=300,t=0)=1.0$としてシミュレーションした、青線が$P(x)$の分布である。

4. 熱力学ポテンシャル

　熱平衡状態もしくはその近傍では、熱力学第２法則(孤立系の熱力学ポテンシャルは極小値へ向かう)を用いて、ゆらぎの緩和過程を扱うことができる。(一方、非平衡系においてはポテンシャル極小のような基本原理が知られていないため不可である) (以下「非平衡系の物理学」§5.7~5.9を参照)

自由エネルギー$F(\lbrace x_i \rbrace,t)$は単調減少しながら熱平衡状態へ緩和していくとして、

\begin{align}
 \frac{dF}{dt} = \sum_i \frac{dx_i}{dt} \frac{\partial F}{\partial x_i} \le 0 
\end{align}

一般に成り立つ正定値行列$\bf{A}$の性質(参考)

\begin{align}
 \bf{x}^T A \bf{x} \geq 0 
\end{align}

を考えると、

\begin{align}
 \frac{dx_i}{dt} \equiv - \sum_i L_{ij} \frac{\partial F}{\partial x_j}  
\end{align}

のような正定値行列$L_{ij}$を定義することで、単調減少条件は自然に満たされる。これは単調減少条件と等価である(ほんとに?)から、系の支配方程式とみなすことができる。熱ゆらぎの項を追加して、

\begin{align}
 \frac{dx_i}{dt} = - \sum_i L_{ij} \frac{\partial \hat F}{\partial x_j} + \xi_i \\
\langle \xi_i(t) \xi_j(0) \rangle = 2M_{Ij} \delta(t)
\end{align}

$M_{ij}$は正定値対称行列である。つまり、これはポテンシャルで書き換えた形(解析力学っぽい)のランジュバン方程式に相当する。時間一階微分の確率微分方程式となっているので、上で見たようにそのままフォッカー・プランク方程式に帰着させることができて、次のような時間発展方程式となる。

\begin{align}
 \frac{\partial P}{\partial t} = \left( \sum M_{ij} \frac{\partial^2}{\partial y_i \partial y_j} + \sum L_{ij} \frac{\partial}{\partial y_i} \frac{\partial \hat F}{\partial y_j} \right) P 
\end{align}

平衡解$\partial P_{eq} /\partial t = 0$を求めることを考える。一般化された揺動散逸定理 "$k_B T L_{ij} = M_{ij}$" が成立すると仮定して、

\begin{align}
 P_{eq} = C \, \mathrm{exp} \left(- \frac{\hat F}{k_B T} \right)
\end{align}

この時、確率流れ$J$を計算すると$J_i=0$が成立する。つまり、「熱平衡状態」というものが「確率流れ0状態」と等価であるという直感的性質を自明とするならば、先程仮定した一般化揺動散逸定理が成立することになる。式をよく見ると、$M_{ij}$が対称行列であったため、$L_{ij}$も自動的に対称行列でなければならない。これを「オンサーガの相反定理」と呼ぶ。

まとめ

1. ミクロな熱ゆらぎを正規分布ノイズとして粗視化することで、ブラウン運動のような確率的にゆらぐ系を定式化したい。
2. 最もシンプルなランダムウォークでは、熱ゆらぎにより粒子がゆっくりと拡散していく現象が見られた。
3. ランダムウォークの離散的設定を連続化することで、粒子の確率分布の時間発展は結局拡散方程式と一致した。
4. 平衡状態では、「ゆらぎによる拡散」と「外力による移流」が釣り合っているはずで、移流拡散方程式を解くと拡散係数と易動度の間に比例関係(揺動散逸関係)が成立した。
5. 運動方程式の形でモデル化(熱ゆらぎを確率変数として取り込んだ確率微分方程式=ランジュバン方程式)しても、揺動散逸関係が再現された。
6. 確率微分方程式を、確率分布の時間発展方程式(フォッカープランク方程式)として書き換えることも出来た。
7. 熱力学第2法則から、熱平衡状態では一般的に揺動散逸定理とオンサーガの相反定理が成立することを証明した。

コメント

1. フォッカープランク方程式を数値計算すれば、確率分布の時間発展が求めるので、細胞内のシミュレーションとかには使えそう？実際の生体ではカオス的な振る舞いもありそうなので、単純にシミュレーションしてもただ初期値や誤差に左右されるだけで意味のある結果出なそうではあるが
2. 各方程式は、熱平衡やその近傍を仮定すれば様々な普遍的性質(線形応答理論・揺動散逸関係・熱力学的ポテンシャルを用いた定式化・オンサーガの相反定理)が導かれるが、一般的な非平衡状態についてはほぼ何もわからない状態。
3. この辺をバイオや医学の分野でゴリゴリ応用していくにはまだまだ遠そう

分子機械 (第9章)

　生体内では熱ゆらぎを利用することで様々な分子機械(ミオシンやポンプ)を作動させている。しかし、熱ゆらぎ自体は、方向性を持たず・エネルギーを取り出すこともできないため、そのままでは機械として効率的に使うことはできない。細胞では主にATPを分解したエネルギーを用いてポテンシャル勾配を作り、一方向への整流作用を実現している。(ここでは主に「非平衡系の物理学」§7を参照した)

1. 状態間の遷移

　複数の谷(極小値)が存在するポテンシャルを持つ系では、熱ゆらぎによって確率的に状態間を遷移することが出来る。ここでは最も簡単な2状態の系について解いてみる。ランジュバン方程式を用いて記述すると、

\left\{
\begin{align}
 &\frac{\partial x}{\partial t} = - \frac{\partial V(x)}{\partial x} + \xi(t) \\
 &V(x) \equiv -\frac{1}{2} x^2 + \frac{1}{4}x^4 - hx \\
 &\langle \xi(t_1) \xi(t_2) \rangle \equiv 2 M \delta(t_1-t_2)
\end{align}
\right.

$F=V(x), L_{ij}=1, M_{ij}=M$の場合に対応するので、フォッカー・プランク方程式は、

\begin{align}
 \frac{\partial P}{\partial t} = \left( M\frac{\partial^2}{\partial x^2} + \frac{\partial}{\partial x}\frac{\partial V}{\partial x} \right) P
\end{align}

平衡状態$\partial P/\partial t =0$では、

\begin{align}
M\frac{d^2 P}{dx^2} &= - \frac{d}{dx} \left( \frac{dV}{dx} P_\mathrm{eq} \right) \\
\rightarrow \, P_\mathrm{eq} &= C\,e^{-\frac{V(x)}{M}}
\end{align}

定常状態では、下図の赤点線のように、ポテンシャル(青点線)が低い方の谷へと集まることがわかった。実際に数値計算を実行した結果は紫線で表している。

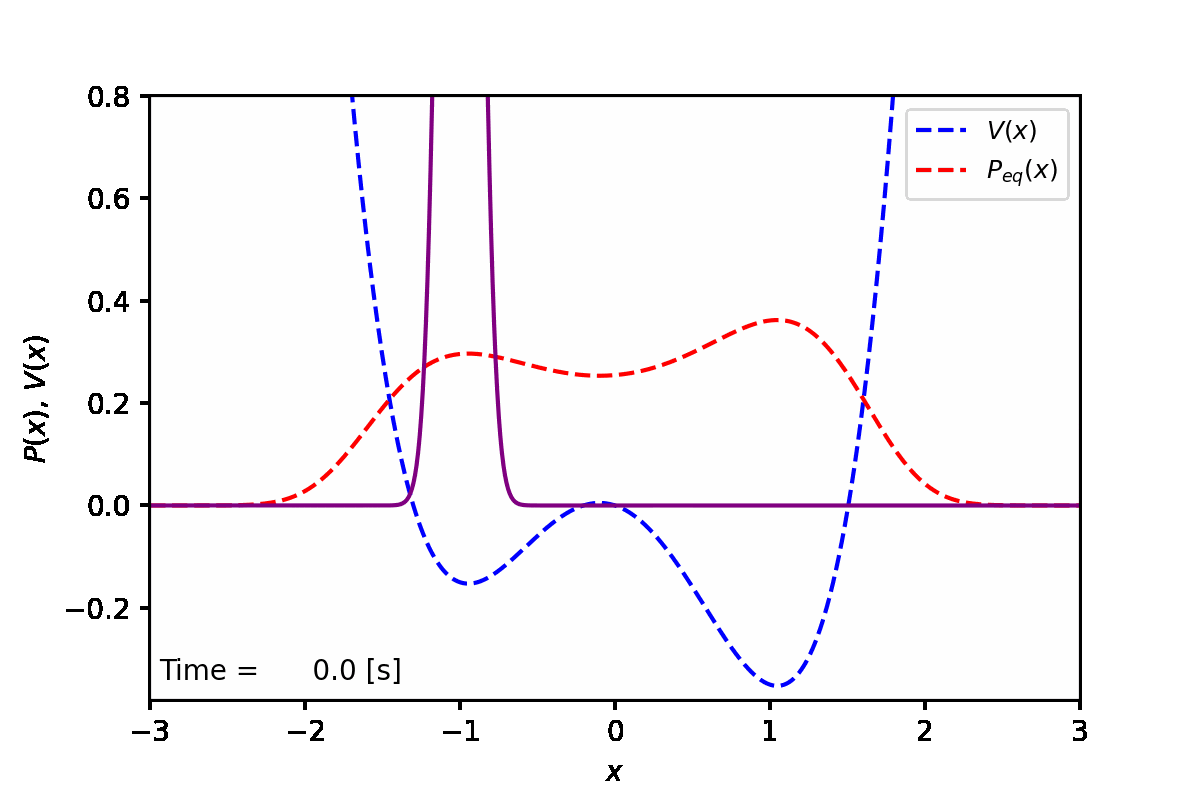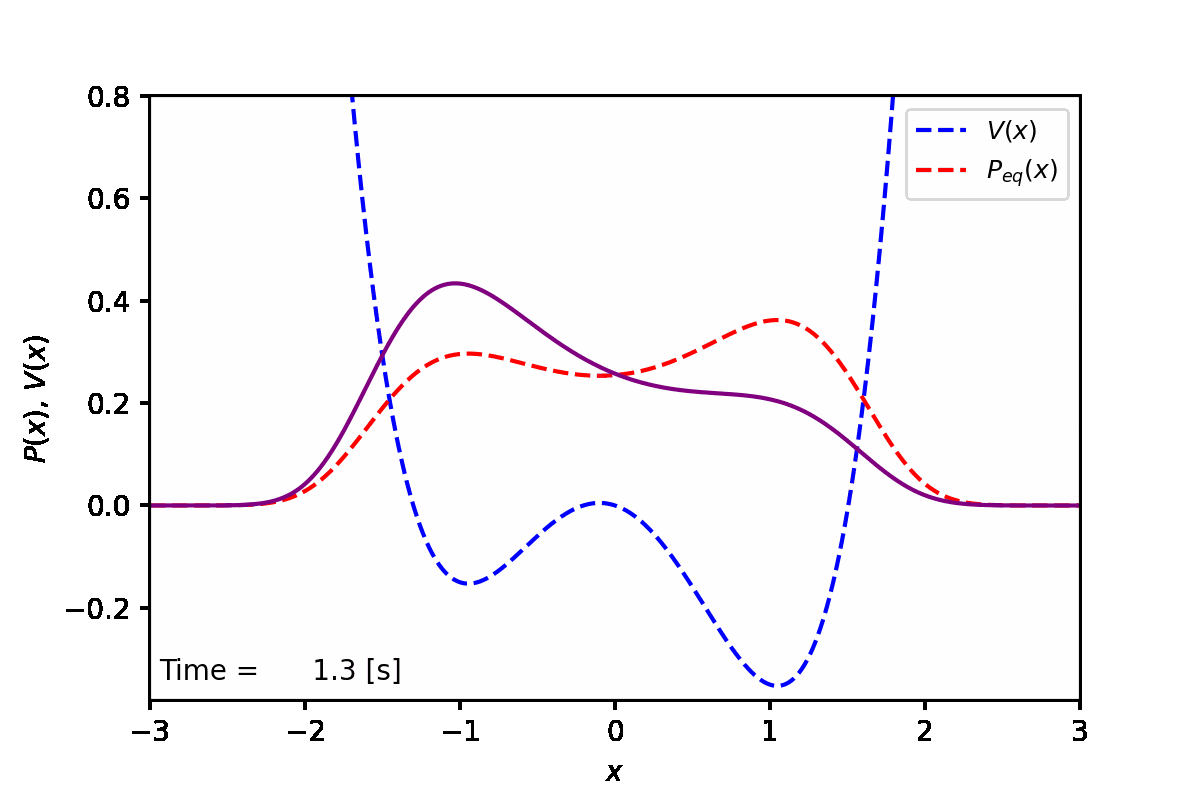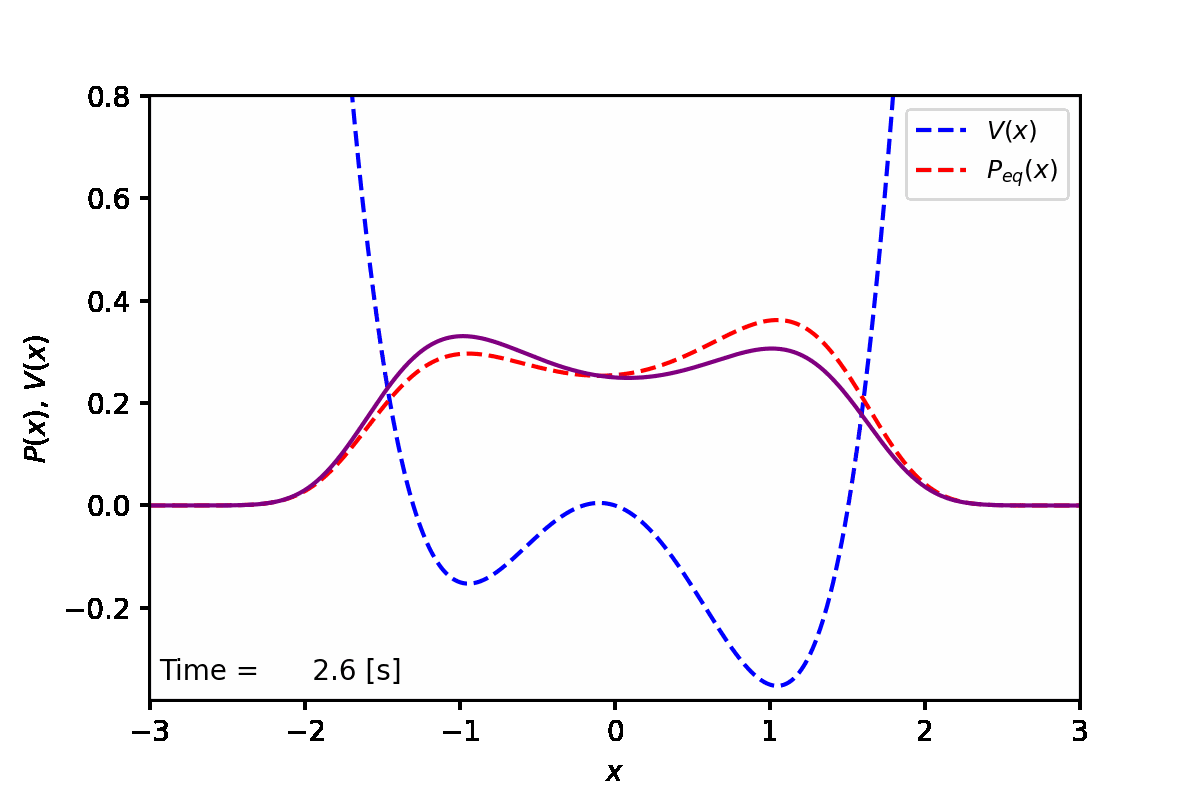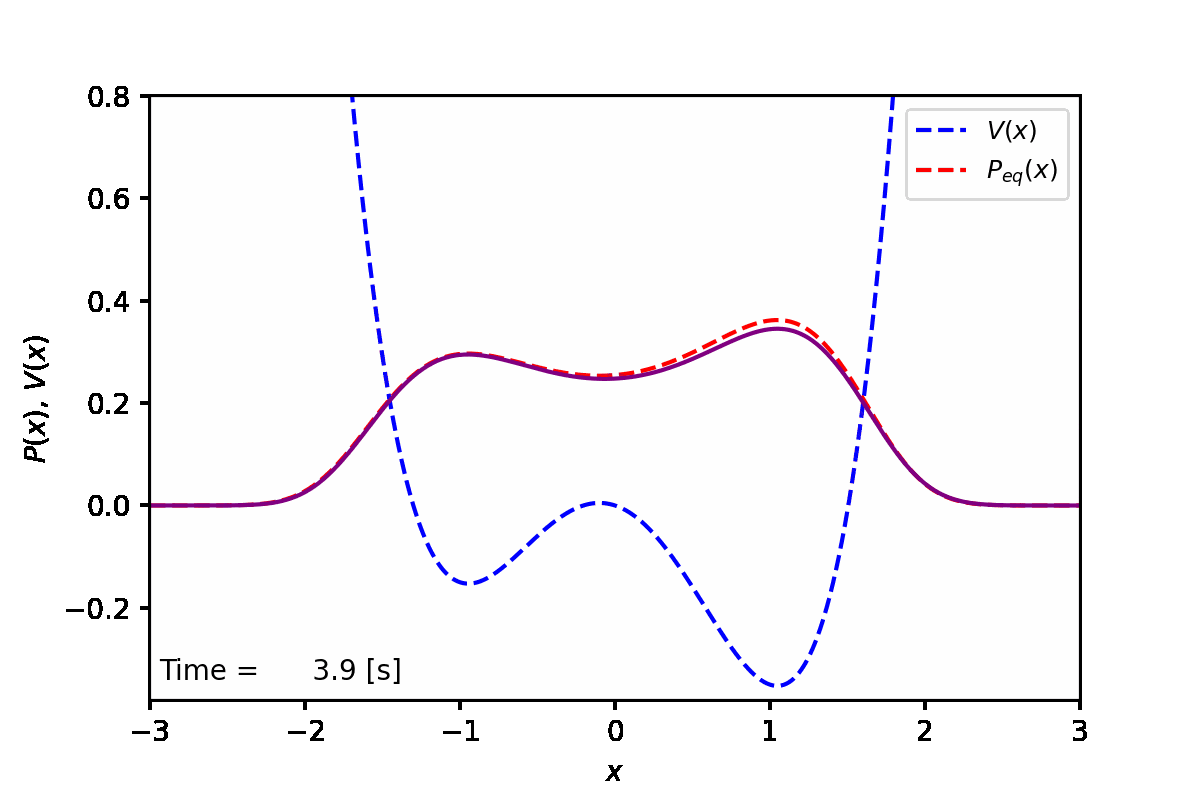
実装例

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

# 初期設定
dt = 0.00004 # 拡散方程式の安定条件：MΔt/Δx^2 < 0.5 (参照:http://www.nibb.ac.jp/miyakohp/asari/htdocs/?page_id=60)
dx = 0.01
min_x = -3.5
num_x = 700
num_t = 100000
h = 0.1
M = 1.0

# ポテンシャルVと平衡状態P_eq
def Func_V(x):
    return -x**2/2.0 + x**4/4.0 - h*x

x_values = np.array([i*0.005-3.0 for i in range(1200)])
y_values = Func_V(x_values)

P_eq = np.exp(-Func_V(x_values)/M)
P_eq /= (np.sum(P_eq)*(0.005))

# フォッカープランク方程式の数値計算
def Trans_x(x):
    return x*dx + min_x

def Trans_t(t):
    return t*dt

def Func_V(x):
    return -x**2/2.0 + x**4/4.0 - h*x

def Func_dV(x):
    return x**3 - x - h

def Func_ddV(x):
    return 3*x**2 - 1

def Gauss(x,u,sigma):
    return np.exp(-(x-u)**2/(2.0*sigma**2)) / (np.sqrt(2*np.pi)*sigma)

def Next_P(t,x):
    x_val = Trans_x(x)
    t_val = Trans_t(t)
    # 拡散 + 移流(?) + 謎の項(?)
    # if(x==0): temp = M*(P[t][1]+P[t][num_x-1]-2*P[t][0])/(dx**2) + Func_dV(x_val)*(P[t][x+1]-P[t][x])/(1.0*dx) + Func_ddV(x_val)*P[t][x] 
    temp = M*(P[t][x+1]+P[t][x-1]-2*P[t][x])/(dx**2) + Func_dV(x_val)*(P[t][x+1]-P[t][x])/(1.0*dx) + Func_ddV(x_val)*P[t][x] 
    return P[t][x] + dt*temp

# 配列 P_xt[t][x]
x_list = np.array([i*dx + min_x for i in range(num_x)])
P = np.array([[0.0 for i in range(num_x)] for j in range(num_t)])

# 初期値は正規分布
u = -1.0
sigma = 0.1

for x in range(num_x):
    P[0][x] = Gauss(Trans_x(x),u,sigma)
    
# メインループ
for i in range(num_t-1):
    t = i
    for x in range(num_x-2):
        P[t+1][x] = Next_P(t,x)
    P[t+1][0] = 0 #P[t+1][1] # 境界条件 適当にやったらうまくいった 
    P[t+1][num_x-1] = P[t+1][num_x-2]
    
    if(i%1000==0):
        print(i)
        plt.plot(x_list, P[i])
        plt.show()

# graph data array
ims = []
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
im_line = ax.plot(x_values, y_values, linestyle = "dashed", color='b',label='$V(x)$')
im_line2 = ax.plot(x_values, P_eq, linestyle = "dashed", color='r',label='$P_{eq}(x)$')

n_plot = 100
interval = num_t / n_plot
for i in range(n_plot-1):
    time = i*interval*dt
    im_line3 = ax.plot(x_list, P[int(i*interval)], color='purple')
    im_time = ax.text(0.01, 0.07, 'Time = {0: 8.1f} [s]'.format(time), verticalalignment='top', transform=ax.transAxes)
    ims.append(im_line + im_line2 + im_line3 + [im_time])
    
# plot
plt.xlim(-3,3)
plt.ylim(-0.38,0.8)
plt.legend(fontsize=9,loc="upper right")
ax.set_xlabel('$x$')
ax.set_ylabel('$P(x)$, $V(x)$')
anm = animation.ArtistAnimation(fig, ims, interval = 50)
anm.save('animation_kaeru.gif', writer = 'pillow', dpi=200)
plt.show()

また、非平衡過程における遷移確率を計算することも出来る。確率流$J$を

\begin{align}
\frac{\partial J}{\partial x} \equiv - \frac{\partial P}{\partial t} 
\end{align}

と定義すると、そのままフォッカープランク方程式の左辺となり、適当に簡略化して計算する(本参照)と、クラマースの遷移率$k$が求まる：

\begin{align}
 k \equiv \frac{J}{n_0} = \frac{\omega_u \omega_m}{2\pi} e^{-\frac{V_u}{M}} 
\end{align}

ミオシン分子による筋収縮

　ミオシン分子は、次のようなサイクルを繰り返す：
「①アクチンと結合 → ②ATPが結合するとアクチンと解離 → ③ATPの加水分解 → ④アクチンの遠位と結合 → ⑤ネック回転で引き込み運動」

④アクチンの遠位と結合するのは、熱ゆらぎによる拡散過程であり、上図(本より引用、図9.5)ではポテンシャル勾配を登る箇所に対応している。⑤引き込み運動は、勾配に沿って動くパワーストロークに対応する。ミオシン分子自体はサイクル一周すると元のエネルギーに戻るが、途中の③ATP加水分解過程により、系全体としてはポテンシャルが低くなっている。このように、分子機械の持つサイクル過程の一部をATPと共役させることで特定の方向へのみサイクルを動かし、熱ゆらぎによる等方的な拡散現象から一方向への運動を取り出していることになる。

実際、ミオシン分子の動きを顕微鏡で観察することで、生体内において熱ゆらぎ現象が利用されていることが初めて実証された：「柳田敏雄：生命現象の基本にゆらぎを発見」

2. ブラウニアンラチェット

　ポテンシャル勾配を動的に切り替えることによっても一方向への運動を取り出すことが出来る。簡単化されたモデルとして、「ブラウニアンラチェット (確率的爪車)」(wikipedia) について扱う。爪車のような左右非対称な「ラチェットポテンシャル」を考えると、これの生成/消去を繰り返すことで、熱ゆらぎする粒子を一方向へと確率的に運動させることができる。本のコードをそのまま使用してシミュレーションした結果：

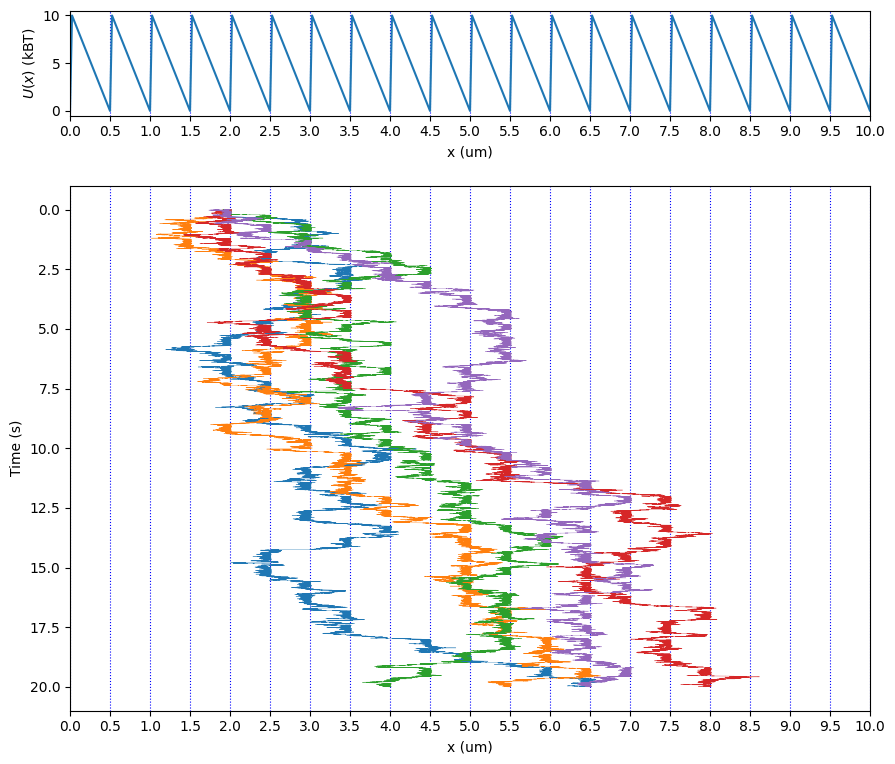
ポテンシャル極小に捉えられた粒子があるとして、ポテンシャルが消滅すると熱ゆらぎ拡散により左右どちらかへランダムで移動する。左へ少し進んだとしてもポテンシャル生成後に元の位置へと戻されるが、右へ進むと次の谷へとさらに進むことができる。エネルギー収支については、ポテンシャル生成時に粒子を持ち上げるために仕事が必要で、消去時にはエネルギー放出される、確率的には吸収より放出するエネルギーが多い(持ち上げられた粒子はポテンシャルが低い谷へ向かう)ので、全体としては負となる。

イオンポンプによる能動輸送

　細胞膜にあるイオンポンプは、細胞内外のイオンを濃度勾配に逆らう方向へ能動輸送を行う。例えば、カルシウムイオンポンプの輸送機構を簡潔にまとめると、熱ゆらぎ拡散により溶液中のCa2+イオンがポンプへと結合する、ここでイオンポンプはATPを加水分解したエネルギーを用いて入り口側を塞ぎ、さらにイオンを出口側へと押し出す(=ラチェットポテンシャル的な仕事を加えたことに相当)。

3. 確率共鳴

　他に、熱ゆらぎを利用した現象として、「確率共鳴」がある。ポテンシャル(外力)が周期的に変化するような系では、熱ゆらぎによって状態が"ぼやける"のではなく逆に"強調"されるという、直感に反する面白い現象が見られる。

例えば、次のような周期ポテンシャル

\begin{align}
 \frac{\partial x}{\partial t} &= - \frac{\partial V(x,t)}{\partial x} + \xi(t) \\
 V(x,t) &= - \frac{a}{2}x^2 + \frac{b}{4}x^4 - xh \cos \Omega t  
\end{align}

を持つ系(下左図)をシミュレーションすると、真ん中図のようにノイズが大きすぎる(上段)と無秩序に振動しているが、ほどほどの場合(中段)には振動が外力と同調して強調されており、ノイズが小さい場合(下段)には外力にゆっくりと同調する振る舞いをすることがわかる。(L. Gammaitoni, et al., Rev. Mod. Phys. 1998)

実際、簡単な場合について($a=b=1,h\ll1$)解くと、

\begin{align}
 \langle x \rangle &= A \cos (\Omega t - \phi) \\
 A &\equiv \frac{h}{M} \frac{2 k_0}{\sqrt{4k_0^2 + \Omega^2}} \\
 k_0 &\equiv \frac{\sqrt{2}}{2 \pi} \exp \left( - \frac{1}{4M} \right)
\end{align}

振幅$A$はゆらぎ$M$に対して上に極大値を持つカーブを描く(上右図)、つまり有限の微小ゆらぎがある場合に強く外力に応答することになる。

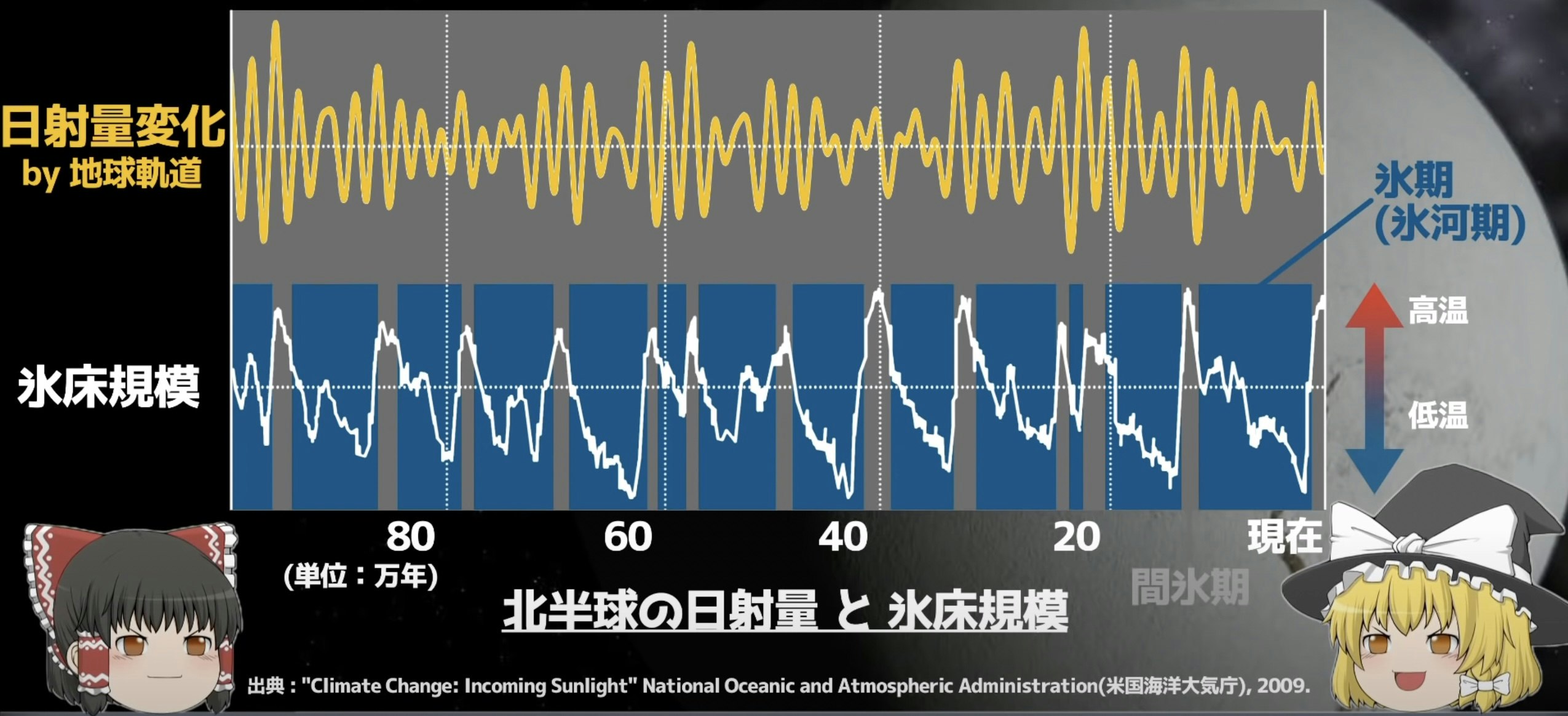
氷河期のモデル

　10万年周期で繰り返すとされている氷河期は、主に地球の公転軌道の離心率(同タイムスケールで変動する唯一の現象？)によるものと考えられている。実際、公転軌道変化から予測される日射量変化に対して、地球気温は鋭敏に反応しているらしい (下図、引用元：地理の雑学ゆっくり解説)。
しかし、離心率の変化による太陽光の照射エネルギーは0.1%程度しか変動しなく、これは大規模な公転軌道の周期的変化に加えて、小規模な太陽活動の変化(ノイズ)があることで、確率共鳴を起こし増幅されているのではないかと言われている。

神経回路

　生体内には微小なノイズが常に存在するので、これを利用して効率的に増幅を起こすような仕組みがあってもおかしくはない。実際、マウスの海馬に周期的な電場+ノイズを加えて神経細胞の発火頻度を計測したところ、微小なノイズを加えた時に最も周期と同調して発火することが確認された (Phys. Rev. Lett, 1996)。
→ 生体における周期的な活動といえば、脳波や心筋細胞などが思い浮かぶ。特に脳波は、脳活動の結果生まれる副産物的な現象を観測していると思っていたが、もしかすると周期的な電磁場の変化を用いて何か情報操作を行っている役割があるのかも？

4. ゆらぎの定理

　熱ゆらぎ系において一般的に成立する「ゆらぎの定理」を用いることで、通常は実験的に観測するのが難しい分子モーターの駆動力や自由エネルギー変化などの物理量を測定することが出来る。(ここでは主に「ヨビノリ ゆらぎの定理@東京理科大学」を参考にした)

[定理] 熱ゆらぎ系の全系のエントロピー生成 $\hat{\sigma} \equiv \Delta S_{系} + \Delta S_{熱浴}$ は次の「ゆらぎの定理(積分型)」を満たす：

\begin{align}
 \langle e^{-\hat{\sigma}} \rangle &= 1 
\end{align}

・熱力学第二法則
$\hat{\sigma}$の一次まで展開(マクローリン展開 $e^{x} = 1+x+O(x^2)$ )すると、次の熱力学第二法則が得られる。エントロピーは基本増大するが、熱ゆらぎによって確率的に破れる場合も許されている。

\begin{align}
 \langle \hat\sigma \rangle &\ge 0 
\end{align}

・揺動散逸定理
$\hat\sigma$がガウス分布であると仮定すると、3次以上のキュムラントが0となる(参考)ので、次の揺動散逸定理が得られる。左辺はゆらぎの大きさ(揺動)を表し、右辺は分散であるから拡散過程(散逸量)を表している。

\begin{align}
 \langle \hat\sigma \rangle &= \frac{1}{2} \left( \langle \hat\sigma^2 \rangle - \langle \hat\sigma \rangle^2 \right) 
\end{align}

・Jarzynski等式
初期条件が熱平衡として系の状態変化を考えると、仕事と自由エネルギーの間に$\hat \sigma = \beta (\hat W - \Delta F)$の関係式が成立し、ゆらぎの定理に代入すると次のJarzynski等式が導出される：

\begin{align}
 \langle e^{-\beta W} \rangle &= e^{-\beta \Delta F}
\end{align}

状態変化は準静的過程である必要は無く、そのような場合に不等式($W\ge\Delta F$：準静的過程でのみ等号が成立)でなく等式の関係式が得られるのは熱力学の分野ではかなりレアな定理。準静的過程を実験的に実現するのは難しい場合があるが、一方Jarzynski等式を用いると、多数回の非準静的過程の実験を行って仕事の期待値から自由エネルギー変化を測定することが出来る。

導出

　ある確率分布$p(x),q(x)$があるとして、$x$は$p(x)$に従うとする：$\langle \cdot \rangle = \sum_x \cdot \ p(x)$。この時、数学的に次の自明な関係式が成り立つ：

\begin{align}
 \langle e^{-ln \frac{p(x)}{q(x)}} \rangle &= 1
\end{align}

$q(x)$はどんな確率分布でもよく、ここにうまいこと物理的な意味を込められれば、物理の定理が作れる！

ここで、時間発展する系の解軌道を$\Gamma$として、その逆過程を$\Gamma^{\dagger}$とする。実現確率をそれぞれ$P(\Gamma)$,$P^{\dagger}(\Gamma^{\dagger})$とする。物理においてミクロな運動方程式は全て時間反転対称性を持つことから、逆過程も必ず正の実現確率を持ち、全部合計すれば1となるはずなので確率分布としての条件を満たす。順過程をたどる確率と逆過程をたどる確率の差は、まさにその系が時間発展でどちらへ進みやすいかを表すもので、熱力学第二法則(時間とともにエントロピー生成が増大)と対応する(詳細ゆらぎの定理)：

\begin{align}
 ln \frac{p(\Gamma)}{p^{\dagger}(\Gamma^\dagger)} &= \hat \sigma (\Gamma)
\end{align}

確率分布$q(x)$として上の逆過程$P^{\dagger}(\Gamma^{\dagger})$を採用すると、「ゆらぎの定理(積分形)」がすぐに導出される。
解軌道$\Gamma$の代わりに、その過程で生じるエントロピー生成$\sigma$を変数にして書き換えたものが、「Crooksゆらぎの定理」である(本人のTwitter)：

\begin{align}
 \frac{p^{\dagger}(-\sigma^\dagger)}{p(\sigma)} &= e^{- \sigma} 
\end{align}

駆動力の測定

　生体における分子モーターは、熱でゆらぎながら何らかの駆動力によって特定の方向へと運動を行う。駆動力を測定できれば、その起源となる分子機構やエネルギー収支が予測できて面白そうである。しかし、そのような微小な力を系を乱さず測定するのは困難である。ゆらぎの定理をうまく使うことで、分子モーターのゆらぎ具合の測定から駆動力を計算することが出来る。(参照：「Fluctuation Theoremによる生体モーターの駆動力測定」)

駆動力$F$で$x$軸正の方向へと移動する分子モーターがあるとして、$\Delta x$移動した際のエントロピー生成(=熱)は$\sigma = \beta W = \beta F\Delta x$である (Jarzynski等式のところの式を使う、自由エネルギー変化は$\Delta F = 0$とした)。すると、ゆらぎの定理に代入して、

\begin{align}
 \frac{p(+\Delta x)}{p(-\Delta x)} &= e^{- \beta F \Delta x} 
\end{align}

分子モーターが正負どちらに$\Delta x$移動するかを多数回測定することで、左辺の確率分布の比が計算でき、そこから右辺にある駆動力$F$を推定出来る。

情報熱力学 (第8章)

　分子機械の章で見たように、生体内ではランダムな熱ゆらぎから、わざわざエネルギーを使って特定の方向の運動を取り出していた。具体例として出てきたミオシン分子・イオンポンプ・ラチェットポテンシャルなどを考えると、ゆらぐ分子の適切なタイミングを見計らって操作を行えば、仕事を加えなくても一方向への運動、つまり仕事が取り出せるのでは？という疑問が生まれる。もし熱ゆらぎからエネルギーを取り出すことができれば、一種の永久機関となり、熱力学第二法則が破られることになる (下図：仕事無しに系のエントロピーを減少させる様子、wikipediaより引用)。

この思考実験において、観測と操作を行うミクロな仮想的存在を「マクスウェルの悪魔(デーモン)」と物理学では慣習的に呼ぶが、実はマクスウェルの悪魔の持つ情報量変化も含めた全系のエネルギー変化を見れば熱力学第二法則には矛盾しないことが示される。これは、直感的には実体を持たない「情報」が、その生成などの操作において物理的なエネルギーや仕事と切り離すことが出来ない、という驚くべき事実に言い換えることも出来る。

実際には、「情報」は記録メモリなど何らかの物理的実体に刻まれるものであり、また情報量をランダムさを表すエントロピーと同一であるとみなすことができ、エントロピーは熱力学で定義される自由エネルギーと関係する物理量である、ことを考えればそれほど不思議ではないのである。(逆に情報の生成/消去を行わないような「可逆的な計算」では原理的にエネルギーを消費せず、量子コンピューターにおけるビット操作などがその代表である。量子ビットは、測定されるまでは、状態ベクトルがヒルベルト空間内をユニタリ変換でぐるぐる回転させられているだけなので可逆計算である。)

以下では、まず議論に必要な「情報量 (シャノンエントロピー)」と「非平衡系での熱力学」について詳しく定義しておき、次に具体例として「シラードエンジン」を扱う。シラードエンジンでは、一見して熱力学第二法則が破れるような系の変化が起きるが、「情報熱力学」を用いて考察することで解決することを見る。結論としては、系から取り出すことの出来る仕事量以上に、デーモンのメモリ処理にはエネルギーが必要であることがわかる。

1. シャノンエントロピー

　ある確率変数$X$がどれだけランダム性を持つかを表す物理量として、次の「シャノンエントロピー(情報量)」を定義する：

\begin{align}
 S(X) \equiv - \sum_{x \in X} P(x) \ln{P(x)}.
\end{align}

$X$の要素$x\in X$は確率分布$P(x)$に従うとしている (例えばサイコロであれば$X=\lbrace 1,2,3,4,5,6 \rbrace$、$P(x)=\frac{1}{6}$となる)。$P(x)$が一様分布の時に$S(X)$は最大値を取ることが簡単に計算でき、これは$X$のランダム性が最も大きく情報量が多いことに対応している。

シャノンエントロピーの定義を2変数に拡張すると、確率変数$X,Y$の2つがあるとして、次のように書ける：

\begin{align}
 S(X,Y) \equiv - \sum_{x \in X, y\in Y} P(x,y) \ln{P(x,y)}.
\end{align}

($X$と$Y$が独立の場合には、$P(x,y)=P(x)P(y)$となることから、確かに$S(X,Y)=S(X)+S(Y)$であることが計算できる)

・条件付きシャノンエントロピー
　$X$と$Y$が相関を持つ場合、$y \ (\in Y)$の値が確定する(=条件)と、$X$が取りうる確率分布にも変化が起きて$S(X)$も変化するはずである。これを「条件付きシャノンエントロピー」と呼び、次のように定義しておく：

\begin{align}
 S(X | y) \equiv - \sum_{x \in X} P(x|y) \ln{P(x|y)}.
\end{align}

ここで、条件確率は$P(x|y) = P(x,y)/P(y)$である。次に、$y$について個別のエントロピーでなく$Y$全体のもとでシャノンエントロピーがどう表せるかを考えてみると、$y$について和を取って

\begin{align}
 S(X | Y) &= \sum_{y\in Y} P(y) \  S(X|y) \\
 &= S(X,Y) - S(Y).
\end{align}

$Y$と$X$を逆にしても同様に、

\begin{align}
 S(Y | X) = S(X,Y) - S(X).
\end{align}

($X$と$Y$が独立であるとすると、$S(X | Y)=S(X)$であるから、確かに$S(X,Y)=S(X)+S(Y)$が成立する。$X$と$Y$が完全に相関しているならば、$S(X | Y)=0$なので、$S(X,Y)=S(Y)$のように直感と一致する。)

・相互情報量
　つまり、条件付きシャノンエントロピーとは、$X$と$Y$の相関度合いを表すような量と言い換えることが出来る。相関を表す「相互情報量 $I(X:Y)$」として、独立な場合には0、完全相関する場合には$S(X)=S(Y)$に一致するような、次の式で定義をする：

\begin{align}
 I(X:Y) \equiv S(X) + S(Y) - S(X,Y) \ge 0.
\end{align}

条件付きシャノンエントロピーで書き換えると、

\begin{align}
 I(X:Y) = S(Y) - S(Y|X) = S(X) - S(X|Y).
\end{align}

この式から、相互情報量とは、「一方の確率変数$X$について観測することで、他方の確率変数$Y$が持つ情報量がどれだけ減少するか」と定めたものであるとも言える。

2. 非平衡熱力学

　非平衡系におけるエントロピーは、シャノンエントロピーに対応している：

\begin{align}
 S(X) \equiv - \sum_{x \in X} P(x) \ln{P(x)}.
\end{align}

(平衡状態でのカノニカル分布を仮定すると、たしかにこの定義でのエントロピーが $F = U - TS$の関係式を満たす物理量であることが確認できるよ)

この時、熱力学第二法則 (クラウジウスの不等式) $\Delta S \ge Q/T$ を書き換えた、次の式を非平衡系でも成り立つ第二法則とする：

\begin{align}
 \sigma \equiv \Delta S - \beta Q \ge 0
\end{align}

出てきた左辺はエントロピー生成と呼ばれる物理量である。(これは様々な非平衡過程のモデルにおいて確かに成立することが確認されている)

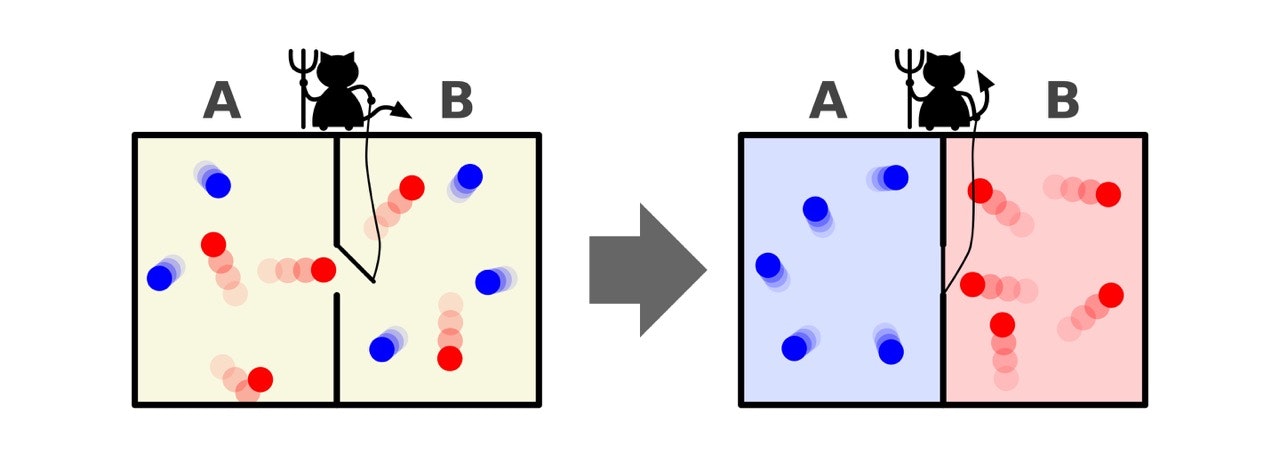
3. シラードエンジン

　次のようなサイクルを持つ熱機関「シラードエンジン」を考える。

1サイクルで外部へ行う仕事量$W_\mathrm{ext}$は、真ん中に入れた仕切りを端へ移動させることで発生し、

\begin{align}
 W_\mathrm{ext} = \int_{V/2}^{V} p dV' = \int_{V/2}^{V} \frac{k_B T}{V'} dV' = k_B T \ln2
\end{align}

となるが、これは正の量なので、熱力学第二法則と矛盾することになる！

一方、測定により減少したシャノンエントロピーは、確率変数が2値の系$X=\lbrace 0,1 \rbrace$、$P(x)=\frac{1}{2}$として考えると、$\Delta S = \ln2$である。この共通した$\ln2$という値を持つ、情報量と仕事量の間には何らかの相関があるのではないかと予想される。

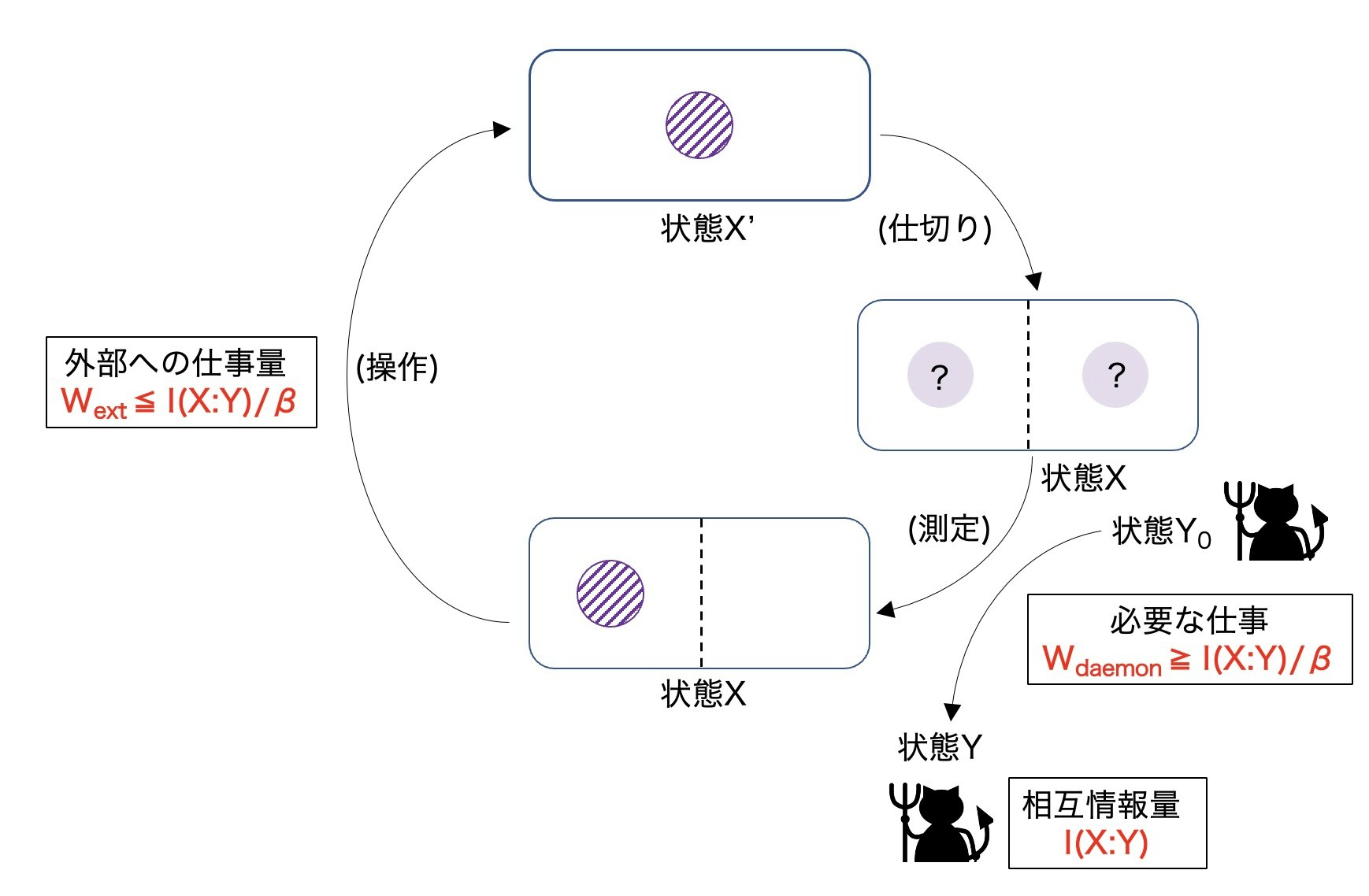
4. マクスウェルの悪魔

　測定とフィードバック操作を行っているマクスウェルの悪魔が物理的な実体を持つメモリであるとして、こいつも含めた全系を考えてみる。このメモリは、0と1の2値を持つもので、それぞれの状態はポテンシャルエネルギー極小の谷にトラップされた状態であるとイメージするとよい。

・フィードバック操作
　システムの状態を $X$、メモリの状態を $Y$ とする。メモリの持つ値 $Y$ によるフィードバック操作でシステムは $X \rightarrow X'$ へと変化するとして、この操作によるエントロピー生成 (全系について第二法則が成立するならば非負) は、

\begin{align}
 \sigma(X,Y) = S(X',Y) - S(X,Y) - \beta Q \ge 0
\end{align}

であり、エントロピー変化を相互情報量を用いて書き換える $S(X',Y) - S(X,Y) = S(X') - I(X':Y) - S(X) + I(X:Y)$ と、

\begin{align}
 \sigma(X,Y) &= S(X') - S(X) - \beta Q - \left[ I(X':Y) - I(X:Y) \right] \\
 &= \sigma(X) - \left[ I(X':Y) - I(X:Y) \right] \\ 
 &\ge 0 \\
 \rightarrow \sigma(X) &\ge I(X':Y) - I(X:Y) \equiv - \Delta I
\end{align}

つまり、相互情報量が減少した分 $- \Delta I$ だけ、系のエントロピー $\sigma(X)$ は負の値を取ることが許されることになる。最大限仕事を取り出すために、$I(X':Y)=0$になるまで操作するとすれば、$\Delta I$ は相互情報量 $I(X:Y)$ そのものと一致する。

取り出せる仕事量 $W_\mathrm{ext}$ については、

\begin{align}
 W_\mathrm{ext} &\le - \left[ F(X') - F(X) \right] - \beta^{-1} \left[ I(X':Y)-I(X:Y) \right] \\
 &= (-\Delta F) + \beta^{-1} \Delta I
\end{align}

であり、やはり相互情報量 $I(X:Y)$ に相当する分だけ増えることが許されているとわかる。この相互情報量は、測定で得られたものであるが、もしこれが無仕事で生み出されるのであれば、やはり熱力学第二法則には矛盾してしまう。そこで、次に測定におけるエントロピー生成と仕事量の変化を見てみる。

・測定
　そこで、次に測定で変化するマクスウェルの悪魔 $Y_0 \rightarrow Y$ のエントロピー生成 $\sigma(Y)$ を考える。上と同じような式が成立するので、初期相関は無い $I(X:Y_0)=0$ として

\begin{align}
 \sigma(Y) &\ge I(X:Y)
\end{align}

つまり、得た相互情報量 $I(X:Y)$ の分だけエントロピー生成が発生している。

デーモンにされる仕事量 $W_\mathrm{meas}$ は、

\begin{align}
 W_\mathrm{meas} &\ge \Delta F_\mathrm{daemon} + \beta^{-1} I(X:Y)
\end{align}

なので、結局は相互情報量 $I(X:Y)$ を生み出すのに、それ以上の仕事をデーモンに加える必要があることがわかった。(自由エネルギー項 $F$ については、エンジンが1サイクルすると正味の変化量が0なので無視してよい。)

・消去
　シラードエンジンをサイクルとするためには、メモリの情報を初期化する必要がある。メモリの持つ2状態のポテンシャル極小値間を移動させるだけなので、必要な仕事はその自由エネルギー差のみである (イメージとしては、ポテンシャルを一度平坦にして、任意の方へ微小な傾きで移動させ、移動後にポテンシャル壁を再形成し、再び初期状態のポテンシャルの形を作ればよい)：

\begin{align}
 W_\mathrm{erase} \ge - \Delta F_\mathrm{daemon} 
\end{align}

・全体まとめ
　結局1サイクルでデーモンに加わる仕事量は、

\begin{align}
 W_\mathrm{daemon} \equiv  W_\mathrm{meas}+ W_\mathrm{erase} \ge \beta^{-1} I(X:Y) 
\end{align}

これが、測定と消去に要する仕事のトレードオフである。

フィードバック操作で取り出せる仕事量と合わせて、1サイクルでの外部への仕事量$W_\mathrm{cycle}$は、相互情報量の項が打ち消し合って

\begin{align}
 \mathbf{W_\mathrm{cycle}} \le W_\mathrm{ext} - W_\mathrm{daemon} = \mathbf{0}
\end{align}

となる。つまり、全系を考えると 熱力学第二法則 に一致した。

シラードエンジンの1サイクルについて総括すると、
1.　まず、仕切りを入れることによって系のエントロピーが減少した。
2.　次に、測定という操作によってデーモン$Y$には系$X$の情報が記録され相互情報量$I(X:Y)$が産まれた。これは減少した系のエントロピー分に対応する。
3.　この時、デーモンのメモリ操作$W_\mathrm{meas}$と初期化には、この相互情報量以上の仕事が必要である。
4.　また、系をフィードバック操作して取り出せる仕事量$W_\mathrm{ext}$は、相互情報量が上限となる(自由エネルギー変化は無視)。
5.　合わせると、1サイクルでの正味の仕事量は、$\mathbf{W_\mathrm{cycle}} \le \mathbf{0}$