細胞膜電位の変化を記述する数理モデルである、「Hodgkin-Huxleyモデル」(1952年に提唱、1963年にノーベル生理学・医学賞を受賞) について、その物理的意味の解説とPythonを用いた実装例を紹介する。
参考文献等
[1] 東京大学大学院 集中講義 (モデルの物理的意味を解説)
[2] Juliaで学ぶ計算論的神経科学 (実装の参考)
[3] 脳神経細胞の活動を数学的に書くHodgkin-Huxleyモデルについて (概説)
膜電位の基礎
細胞膜は、細胞内液と細胞外液を物理的に分離し、それぞれのイオン濃度の違いによって膜の内外に電位差が生じることになる(下図左)。外部刺激により電位依存性イオンチャネルが開口すること等でイオン濃度のバランスが崩れ、膜電位は様々に変化する(下図右)。
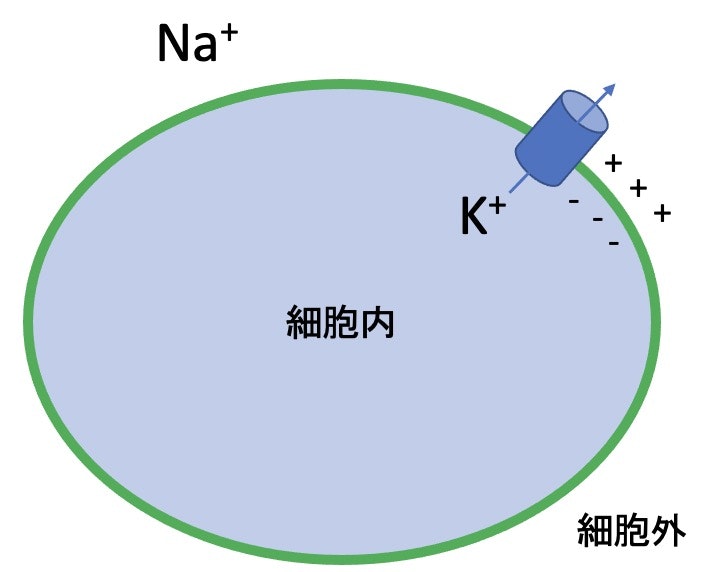
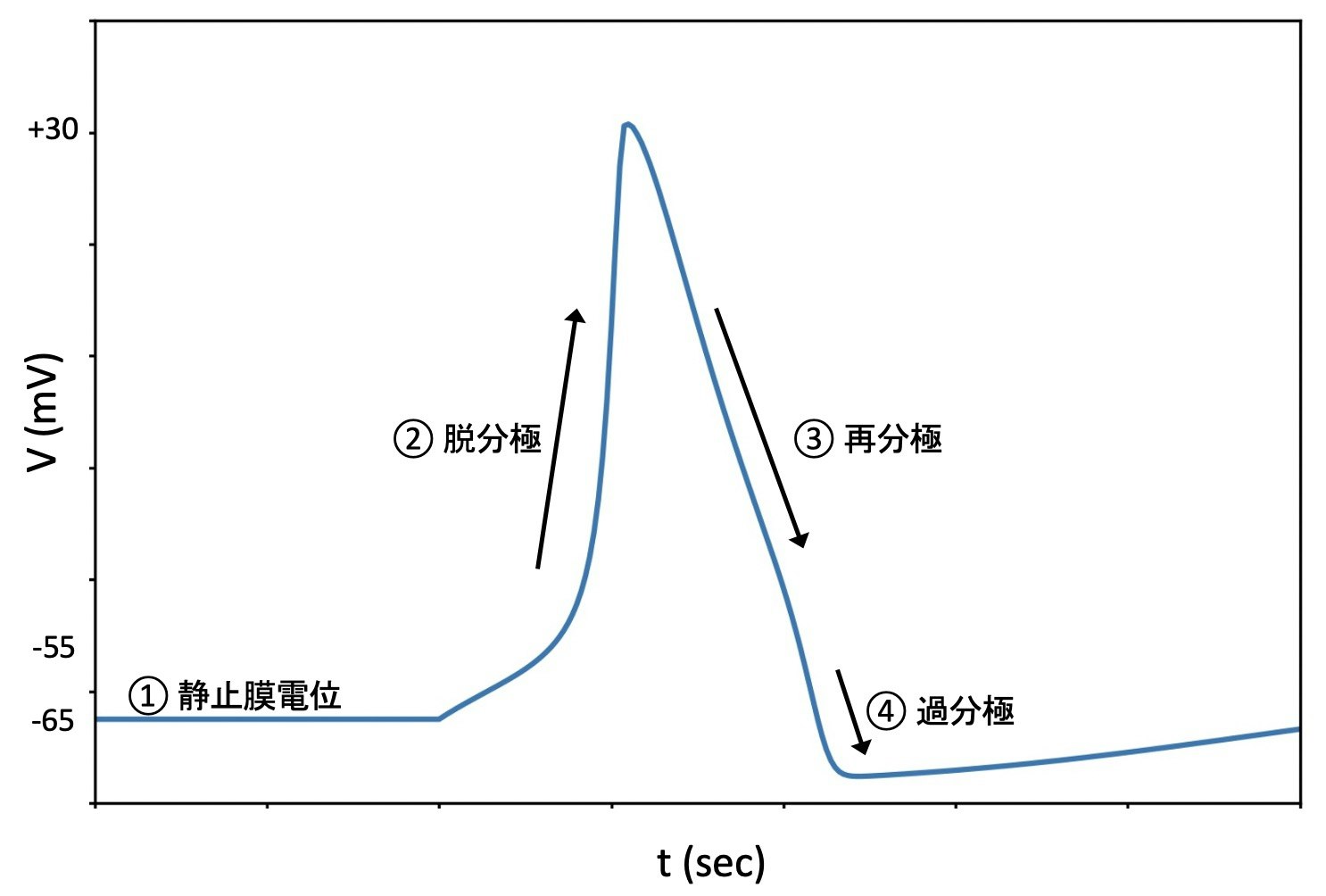
① 静止膜電位:外部からの刺激が無い状態での電位差を静止膜電位と呼び、細胞外を基準にして細胞内はおよそ -65 mV の値を取る。通常、細胞膜には $\mathrm{Na}^+/\mathrm{K}^+$ポンプが発現しており、細胞外へ$\mathrm{Na}^+$イオン・細胞内へ$\mathrm{K}^+$イオンを汲み出している。細胞膜には他に$\mathrm{K}^+$チャネルがあり、これを通して$\mathrm{K}^+$イオンが細胞外へ流出することで、膜を挟んだ電気二重層が形成される。これが平衡膜電位を生み出す起源となる。
② 脱分極:この平衡状態が崩れるのは、外部から電気刺激が入った時である。神経細胞の電位依存性$\mathrm{Na}^+$チャネルはある閾値電位(-55 mV)を超えると開き、$\mathrm{Na}^+$イオンが細胞内に大量に流入することで、膜電位は急速に高まり$\mathrm{Na}^+$イオンの静止電位 (+50 mV)へと近づく。
③ 再分極:$\mathrm{Na}^+$チャネルは開口後一定時間経過により不活性化する。これと同じタイミングで、反応の遅い電位依存性の$\mathrm{K}^+$チャネルが開口し、元の静止膜電位へ向けて再分極が進む。
④ 過分極:$\mathrm{Na}^+$チャネルが完全に閉じ、電位依存性$\mathrm{K}^+$チャネルが開いた状態では、膜電位は静止膜電位よりさらに低い電位へと落ちこむ。これを過分極と呼び、$\mathrm{K}^+$チャネルの閉口と共にゆっくりと静止膜電位へ戻っていく。
$\mathrm{Na}^+$チャネルの不能期が終わると、再び①〜④のような脱分極からのサイクルが可能になる。神経伝達では、神経細胞の一部に脱分極が生じると、その影響で近くの電位依存性$\mathrm{Na}^+$チャネルが脱分極し、...とこれが次々と膜上を伝わっていく。
このような電位変化を数理モデルによって記述するには、イオンを選択的に透過させるイオンチャネルの化学的性質 (電位差に反応して開口し、一定時間で不活化するなど) を取り入れたモデル化が必要である。
Hodgkin-Huxleyモデルの物理的意味
HodgkinとHuxleyは、膜電位に関わる要素(細胞膜・イオンチャネル)を次のようにモデル化した電気回路として数式を立てた(下図参照)。
・脂質二重膜は電荷(イオン)を通さないコンデンサー:
\begin{eqnarray}
I_m = C_m \frac{dV(t)}{dt} \tag{1}
\end{eqnarray}
・イオンチャネルは、そのイオン$\alpha$の通りやすさを可変抵抗(伝導度$g_{\alpha}$)で、濃度勾配による拡散力を電位差(平衡電位$E_{\alpha}$)で表す:
\begin{eqnarray}
I_{\alpha} = g_{\alpha} (V - E_{\alpha}) \tag{2}
\end{eqnarray}

回路を流れる電流の保存則(キルヒホッフの法則)より、
\begin{eqnarray}
I_{ext} = I_m + I_K + I_{Na} + I_L \tag{3}
\end{eqnarray}
$I_{ext}$は、実験時に電気刺激として外部から強制的に流す電流の大きさである。$I_K,I_{Na}$はイオン$\mathrm{K}^+$,$\mathrm{Na}^+$がイオンチャネルを通って流れることによる電流、$I_L$は他のイオンが漏れ流れることによる電流を表す。
イオンチャネル
上記の数式化によるモデル化では、まだ取り入れられていない要素がある。それは、電位依存性イオンチャネルが電気刺激(電位差)によって開閉し、またその開閉が瞬時ではなく時間差によって起こる、という物理現象である。これを可変抵抗の伝導度$g_{\alpha}$が$g_{\alpha}(V,t)$のように、変数$V,t$に依存するとしてモデル化を試みる。
K+イオンチャネル
実は電位依存性$\mathrm{K}^+$イオンチャネルは4つのサブユニットから構成され、それぞれが電気刺激によって独立に開いたり閉じたりしている。サブユニットが全て開いている時にのみ$\mathrm{K}^+$イオンは透過することが出来る。つまり、1つのサブユニットが開いている確率を$n$と置くと、伝導度$g_{K}$は
\begin{eqnarray}
g_K = \bar{g}_K \cdot n^4(V,t) \tag{4}
\end{eqnarray}
のように$n^4$に比例する形で書ける*。$\bar{g}_K$はイオンチャネルが完全に開いている場合の伝導度であり、これは時間・電位依存性も持たない。
(*実際に電位依存性$\mathrm{K}^+$イオンチャネルが4つのサブユニットを持つ立体構造であると判明したのは46年後の1998年である (R.MacKinnonがこの業績により2003年にノーベル化学賞を受賞)。HodgkinとHuxleyはイオンチャネルの物理的実体などは全く知らない状態で、実験結果と考察のみからこの数式化を導いた。)


では、$n$はどのような電位依存性と時間依存性を持てばよいだろうか?初期状態$t=0$である値$n_0$を取るとすれば、一定の電位$V$をかけ続ければある収束値$n_{\infty}$($V$と共に増大)に時間とともに漸近していくと予想される(上図左)。このような振る舞いをするモデルはいくつも考えられるが、実験的事実と照らし合わせることで次のような時間発展方程式
\begin{eqnarray}
n(t) = n_\infty + (n_0 - n_\infty) e^{-\frac{t}{\tau}}
\end{eqnarray}
で表されるものとする。実際に論文で使われたパラメータ値から、様々な電位$V$(一定)を与えたときの振る舞いをプロットした(上図右)。$t=0$で$n=n_0$、$t$が増加するにつれて急速に$n_\infty$に近づくことがわかる。
実際に電位$V$は時間によって変化するため、このままではシミュレーションすることが難しい。上式を解に持つような微分方程式は、
\begin{eqnarray}
\frac{dn(t)}{dt} = \alpha_n(V) (1-n) - \beta_n(V) n \tag{5}
\end{eqnarray}
のように書けるため、シミュレーションにはこの方程式を時間差分化して解くことになる。関数$\alpha_n(V),\beta_n(V)$は、実験とフィッティングして決められるものであり、後に具体形を示す。
(上記微分方程式を解くと、積分定数$A$として、
\begin{eqnarray}
\frac{dn(t)}{dt} = \alpha - (\alpha + \beta) n \\
n(t) = \frac{\alpha}{\alpha+\beta} + A e^{-(\alpha+\beta)t}
\end{eqnarray}
となり、解が上式と同じ形になることがわかる)
Na+イオンチャネル
電位依存性$\mathrm{Na}^+$イオンチャネルでは、さらに不能期という時間経過により不活性化する要素を加える必要がある。$\mathrm{K}^+$イオンチャネルと似たような形で、伝導度$g_{Na}$は
\begin{eqnarray}
g_{Na} = \bar{g}_{Na} \cdot m^3(V,t) \cdot h(V,t) \tag{6}
\end{eqnarray}
のような式で表すことにする。$m$は$n$と似たような意味合い(チャネルの活性化)を持ち、$h$は逆に不活性化を表すパラメータである。実際に論文で使われたパラメータ値から、様々な電位$V$(一定)を与えたときの$m,h,m^3h$の振る舞いをプロットした(下図)。たしかに時間と共に開口・閉口していく様子が再現できている。
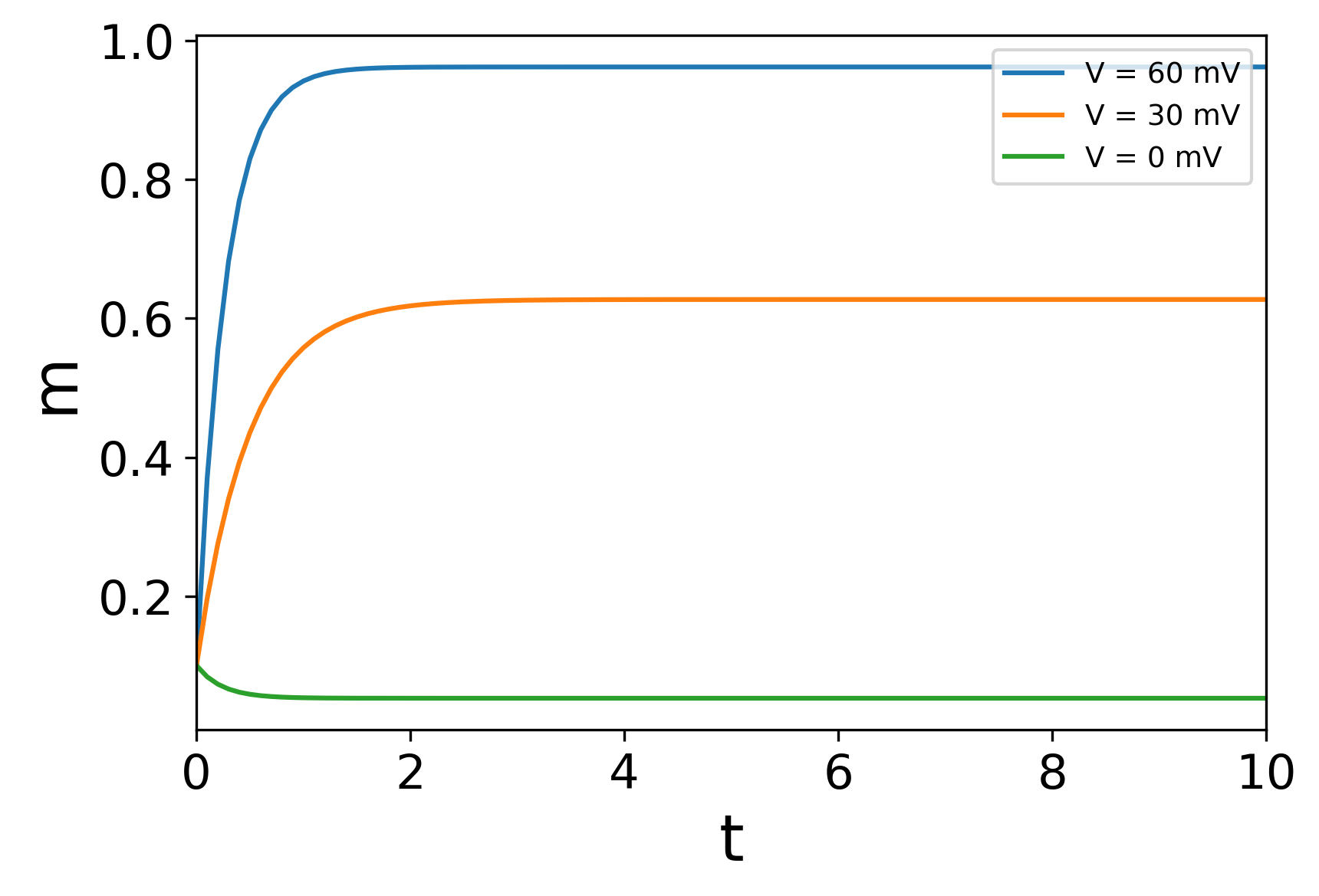
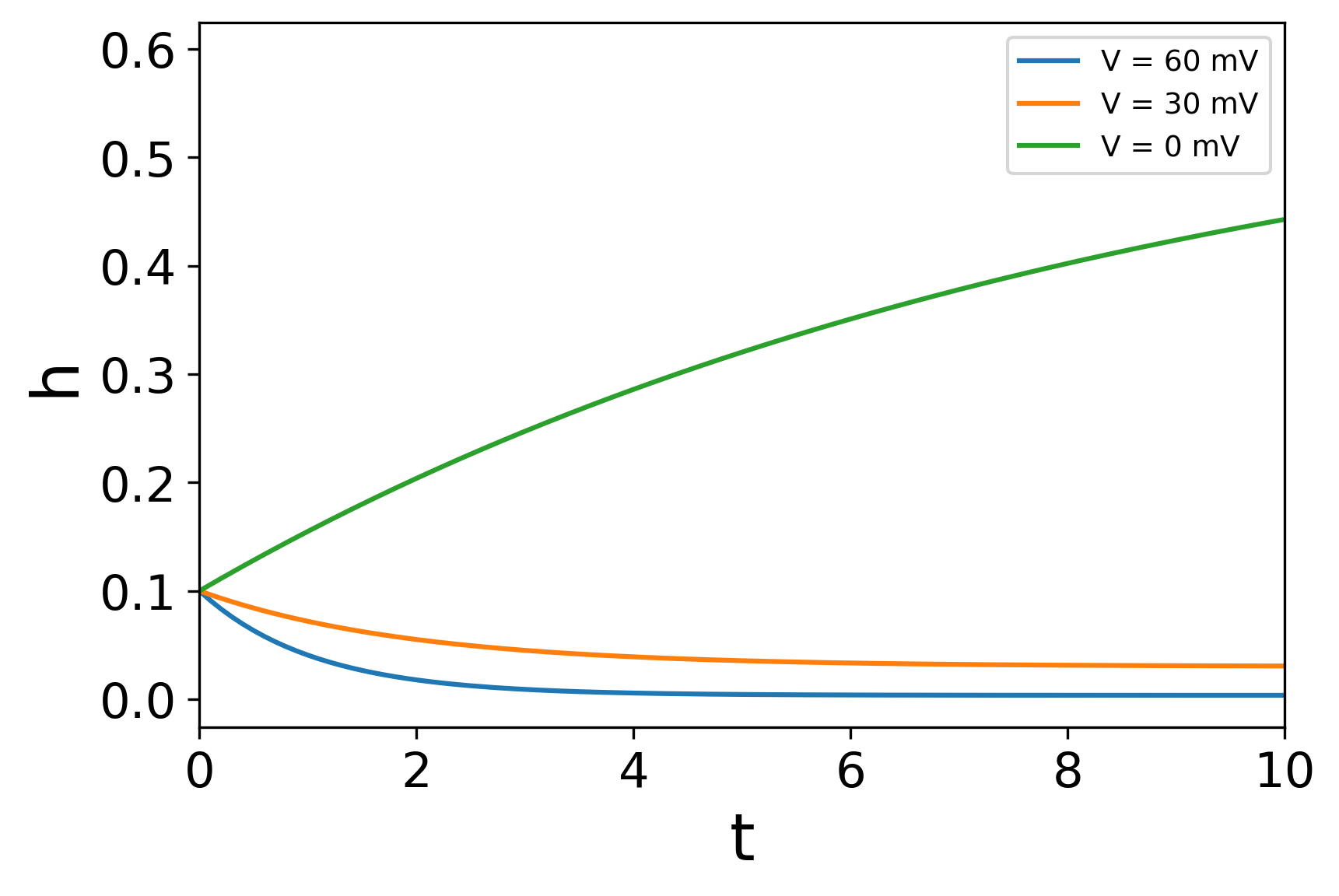
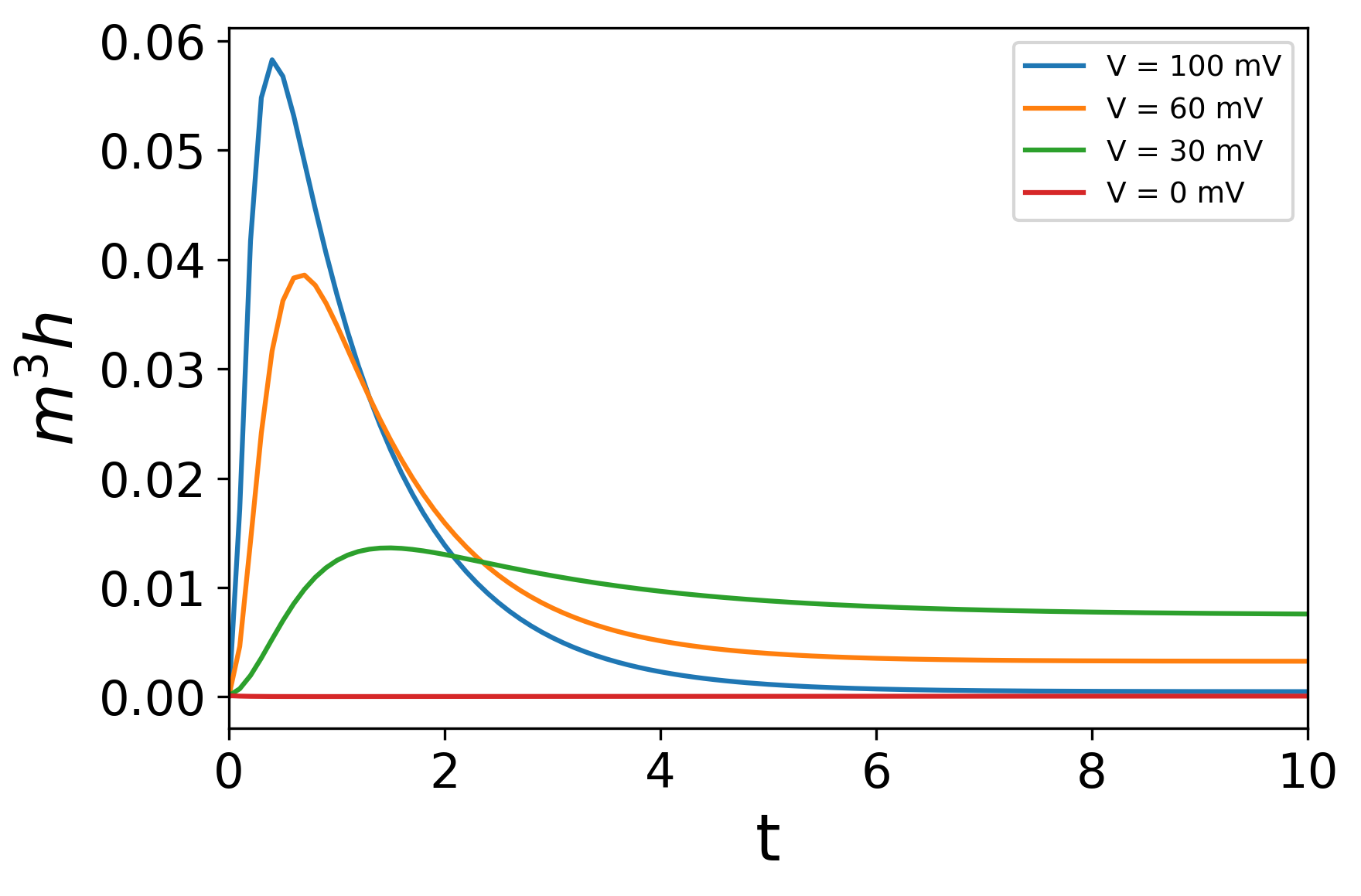
それぞれが$n$と同じ形の微分方程式に従うとし、
\begin{eqnarray}
\frac{dm(t)}{dt} = \alpha_m(V) (1-m) - \beta_m(V) m \tag{7} \\
\frac{dh(t)}{dt} = \alpha_h(V) (1-h) - \beta_h(V) h \tag{8}
\end{eqnarray}
リーク電流
リーク電流は主に$\mathrm{Cl}^-$イオンの漏出によるもので、その伝導度$g_L$は電位に依存せず、
\begin{eqnarray}
g_{L} = \bar{g}_{L} \tag{9}
\end{eqnarray}
となる。
Pythonによる実装
式(3)に式(1)(2)(4)(6)(9)を代入して、
\begin{eqnarray}
I_{ext} = C_m \frac{dV(t)}{dt} + \bar{g}_K \cdot n^4 \cdot (V-E_{K}) + \bar{g}_{Na} \cdot m^3 \cdot h \cdot (V-E_{Na}) + \bar{g}_{L} \cdot (V-E_L)
\end{eqnarray}
微分項を差分化($\frac{dV}{dt}=\frac{V(t+\Delta t)-V(t)}{\Delta t}$)・整理して、
\begin{eqnarray}
V(t+\Delta t) = V(t) + \frac{\Delta t}{C_m} \left( I_{ext} + \bar{g}_K \cdot n^4 \cdot (E_{K}-V) + \bar{g}_{Na} \cdot m^3 \cdot h \cdot (E_{Na}-V) + \bar{g}_{L} \cdot (E_L-V) \right)
\end{eqnarray}
伝導度に関するパラメータ$n,m,h$は、時間微分方程式(5)(7)(8)を差分化して、
\begin{eqnarray}
n(t+\Delta t, V) &=& n(t, V) + \Delta t \cdot \left[ \alpha_n(V) (1-n) - \beta_n(V) n \right] \\
m(t+\Delta t, V) &=& m(t, V) + \Delta t \cdot \left[ \alpha_m(V) (1-m) - \beta_m(V) m \right] \\
h(t+\Delta t, V) &=& h(t, V) + \Delta t \cdot \left[ \alpha_h(V) (1-h) - \beta_h(V) h \right]
\end{eqnarray}
の式によって更新していく。
具体的なパラメータは実験から決められる。[1]から引用すると、
\begin{eqnarray}
C_m=1.0, \bar{g}_{Na}=120, \bar{g}_{K}=36, \bar{g}_L=0.3, E_{Na}=50.0, E_{K}=-77, E_{L}=-54.387,
\end{eqnarray}
\begin{eqnarray}
\alpha_n(V) &=& \frac{0.01(10-V)}{\mathrm{exp}[(10-V)/10] - 1} \\
\beta_n(V) &=& 0.125 \, \mathrm{exp}(-V/80) \\
\alpha_m(V) &=& \frac{0.1(25-V)}{\mathrm{exp}[(25-V/10)]-1} \\
\beta_m(V) &=& 4 \, \mathrm{exp}(-V/18) \\
\alpha_h(V) &=& 0.07 \, \mathrm{exp} (-V/20) \\
\beta_h(V) &=& \frac{1}{\mathrm{exp}[(30-V)/10] + 1} \\
\end{eqnarray}
ただし、ここでの$V$は平衡電位$V_{eq}=-65$(mV)を基準にした値であるようなので、プログラミングの際には関数に$V-V_{eq}$の値を代入することにする。
以下に実装例を紹介する。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# 関数の定義
def Alpha_m(V):
return 0.1*(25-V) / (np.exp((25-V)/10.0) - 1)
def Beta_m(V):
return 4.0 * np.exp(-V/18.0)
def Alpha_h(V):
return 0.07 * np.exp(-V/20.0)
def Beta_h(V):
return 1.0 / (np.exp((30-V)/10.0) + 1)
def Alpha_n(V):
return 0.01*(10-V) / (np.exp((10-V)/10.0) - 1)
def Beta_n(V):
return 0.125 * np.exp(-V/80.0)
# パラメータ等の設定
dt = 0.05
num_steps = 7000
C_m, g_Na, g_K, g_L = 1.0, 120.0, 36.0, 0.3
E_Na, E_K, E_L = 50.0, -77.0, -54.387
V_eq = -65.0
t = np.array( [i*dt for i in range(num_steps)] )
m = np.zeros(num_steps)
h = np.zeros(num_steps)
n = np.zeros(num_steps)
V = np.zeros(num_steps)
I = np.zeros(num_steps)
m[0], h[0], n[0], V[0] = 0.05, 0.6, 0.32, -65.0 # 初期値
I[1000:2000] = 2 # 微弱電流
I[3000:4000] = 10 # 脱分極
I[5000:6000] = 30 # 脱分極
# 微分方程式を解く
for i in range(num_steps-1):
m[i+1] = m[i] + dt*( Alpha_m(V[i]-V_eq)*(1-m[i]) - Beta_m(V[i]-V_eq)*m[i] )
h[i+1] = h[i] + dt*( Alpha_h(V[i]-V_eq)*(1-h[i]) - Beta_h(V[i]-V_eq)*h[i] )
n[i+1] = n[i] + dt*( Alpha_n(V[i]-V_eq)*(1-n[i]) - Beta_n(V[i]-V_eq)*n[i] )
V[i+1] = V[i] + dt*( I[i] - g_Na*(m[i]**3)*h[i]*(V[i]-E_Na) - g_K*(n[i]**4)*(V[i]-E_K) - g_L*(V[i]-E_L) )
# グラフにプロット
plt.figure(dpi=300)
plt.xlim(0,350)
plt.ylim(-80,80)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.xlabel("t (sec)",fontsize=20)
plt.ylabel("V, I",fontsize=20)
plt.plot(t, V, '-', label="voltage V")
plt.plot(t,I, '-', label="current I_ext")
plt.legend(fontsize=9,loc="upper right")
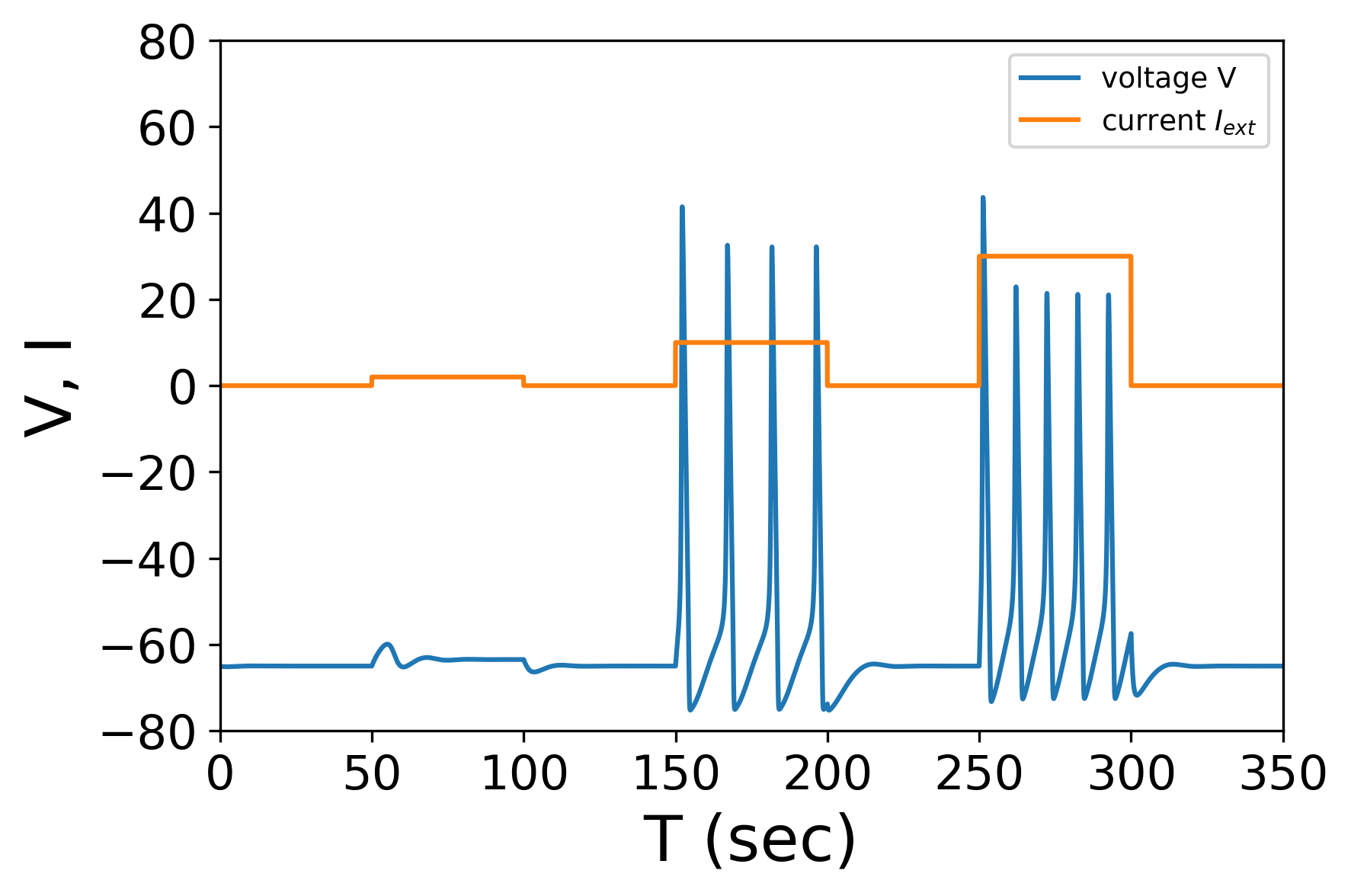
外部電流が小さい場合(50~100 sec)には脱分極が起きず、大きい場合(150~200 sec)には脱分極・再分極・過分極を繰り返す様子が再現できている。さらに電流を大きく(250~300 sec)しても、脱分極の最大値がほぼ変化していない・繰り返し周期は少し短くなるという特徴が観察された。
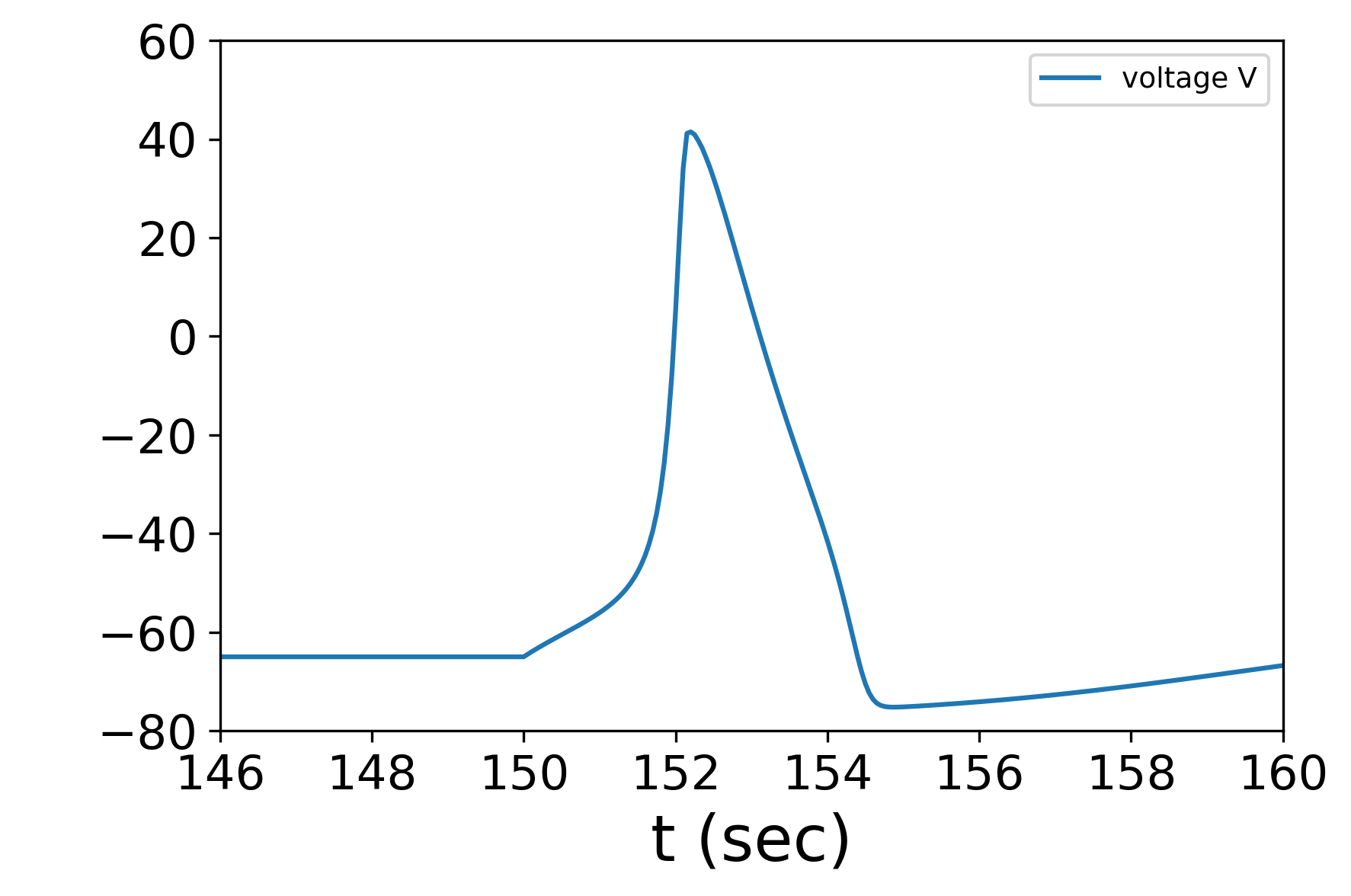
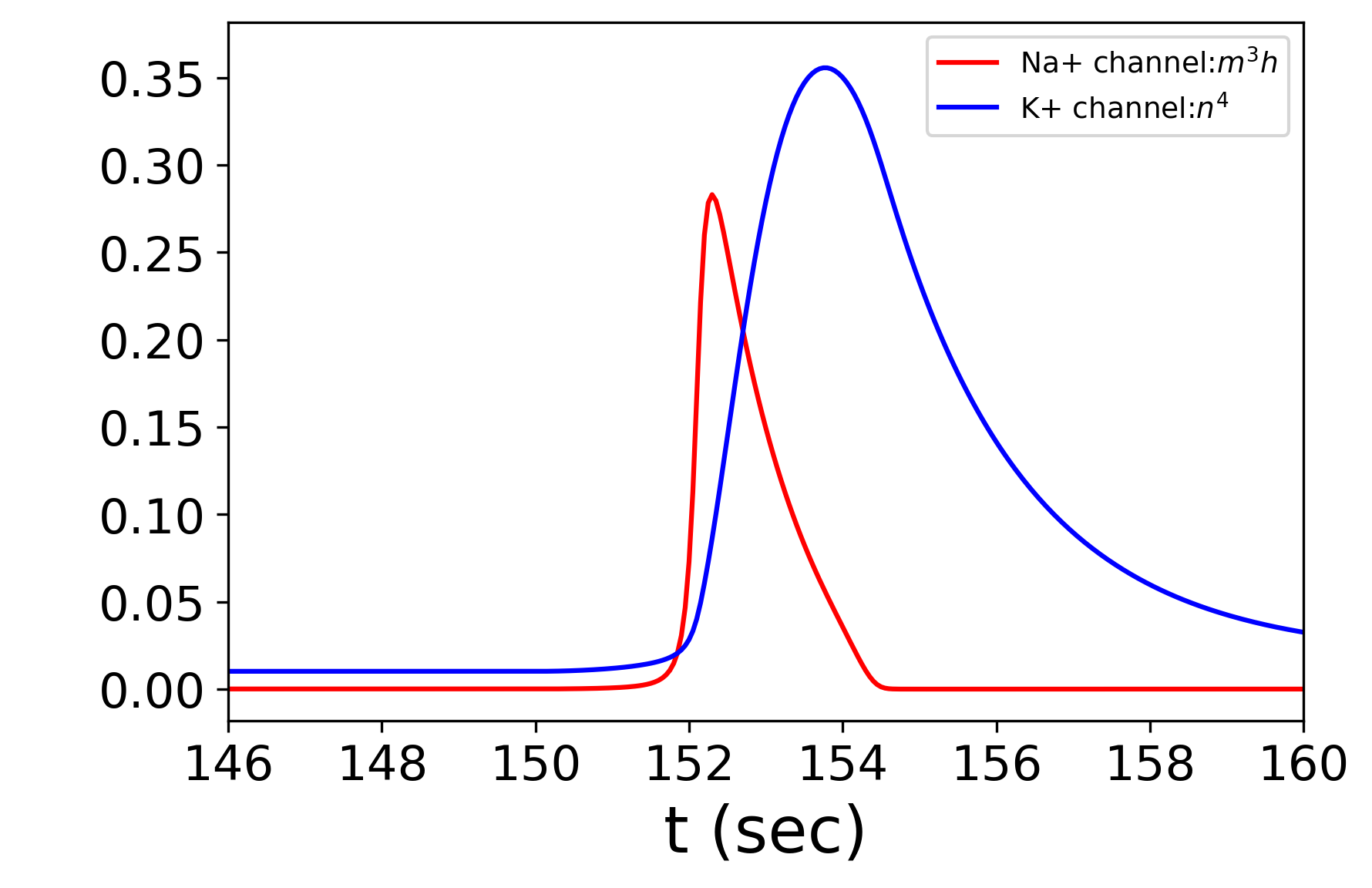
1サイクルを詳しく見てみると、外部電流に呼応して電位が増していき(150~152 sec)、一定値を超えた瞬間(152 sec付近)で急速に$\mathrm{Na}^+$チャネルが開口して脱分極、$\mathrm{Na}^+$チャネルが閉じ始めるのと同時期に$\mathrm{K}^+$チャネルが遅れて開口することで再分極、そのまま過分極を引き起こす様子がわかる。