適当まとめ。
[参考文献等]
・導出パート
予備校のノリで学ぶ「大学の数学・物理」 (Youtube解説動画)
・実装パート
非圧縮性 Navier-Stokes 方程式の数値解法 (Qiita記事)
・その他
Fluid Simulation for Computer Graphics (CG分野の教科書)
A Tutorial in Grid Based and Particle Based Methods (↑の実装に必要partだけ解説したやつ)
CGのための物理シミュレーションの基礎 (日本語教科書)
流体シミュレーションにおける様々な手法 (日本語解説スライド)
Navier-Stokes方程式
まずはNavier-Stokes方程式の導出について。流体を場によって表現するとし、位置${\bf r}$,時刻$t$を変数とした速度場$\vec{u}({\bf r},t)$を定義する。同様に、液体の性質と状態を一意に定める変数(圧力$P$、密度$\rho$)と外力($F_{ext}$)を定義しておく(今回は非粘性液体、非圧縮流体のみを考える、外力としては重力$-g$を想定)。Navier-Stokes方程式は次のようにになる:
\begin{eqnarray}
\frac{\partial\vec{u}}{\partial t} + (\vec{u}\cdot\nabla)\vec{u}
= -\frac{1}{\rho}\nabla P + \vec{F}_{ext} \tag{1}
\end{eqnarray}
直感的には、古典的なニュートン運動方程式に類似したものとして捉えることができる。質量$m$の物体が速度$\vec{u}(t)$で動くとしたときの運動方程式は、
\begin{eqnarray}
m \frac{\partial \vec{u}(t)}{\partial t} = \vec{F}_{Newton}
\end{eqnarray}
これを流体に適応するとして、液体中の微小立体の運動を考えてみる。

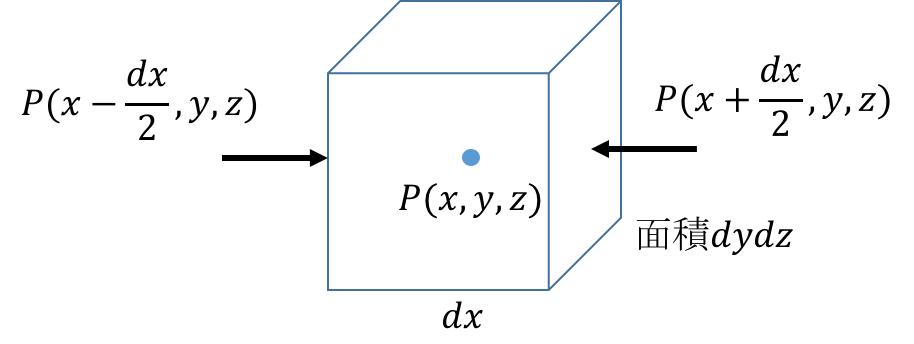
液体中に存在する場合、上下左右の液体からの圧力を受けるので圧力項を加える。受ける圧力は正味で$-(\nabla P) dxdydz$のようになる(下の圧力項参照).
質量項を$m=\rho\cdot dxdydz$のように密度と微小体積で置き換えると、
\begin{eqnarray}
\rho\cdot dxdydz \frac{\partial \vec{u}(t)}{\partial t} = -(\nabla P) dxdydz + \vec{F}_{Newton}
\end{eqnarray}
両辺を質量項で割ると、
\begin{eqnarray}
\frac{\partial \vec{u}(t)}{\partial t}
&=& -\frac{1}{\rho}\nabla P + \frac{\vec{F}_{Newton}}{m} \\
&=& -\frac{1}{\rho}\nabla P - g
\end{eqnarray}
外力を重力のみに限定すれば、外力項は$-g$となる。式(1)と比較すると、Navier-Stokes方程式とほぼ同じ、左辺に$(\vec{u}\cdot\nabla)\vec{u}$の項だけが足りていないことがわかる(移流項へ)。
圧力項
\begin{eqnarray}
P(x-\frac{dx}{2})dydz-P(x+\frac{dx}{2})dydz
\end{eqnarray}
のようになり、位置$x$周りのTaylor展開を行うと、
\begin{eqnarray}
&=& \left[ \left(P(x) - \frac{\partial P}{\partial x}\left(\frac{dx}{2}\right) + O\left(dx^2\right)\right)
- \left( P(x) + \frac{\partial P}{\partial x}\left(\frac{dx}{2}\right) + O\left(dx^2\right) \right) \right]dydz \\
&\simeq& - \frac{\partial P}{\partial x} dxdydz
\end{eqnarray}
$y,z$軸方向についても同様に導出できて、
\begin{eqnarray}
\begin{pmatrix}
- \frac{\partial P}{\partial x} dxdydz \\ - \frac{\partial P}{\partial y} dxdydz \\ - \frac{\partial P}{\partial z} dxdydz
\end{pmatrix}
= - (\nabla P) dxdydz
\end{eqnarray}
となる。
移流項 (Advection)
上記Navier-Stokes方程式の左辺
\begin{eqnarray}
\frac{\partial\vec{u}}{\partial t} + (\vec{u}\cdot\nabla)\vec{u}
\end{eqnarray}
は速度場に関する時間微分と空間微分が少し複雑に組合わさった形になっている。ここに質点の運動方程式との違いが現れている。
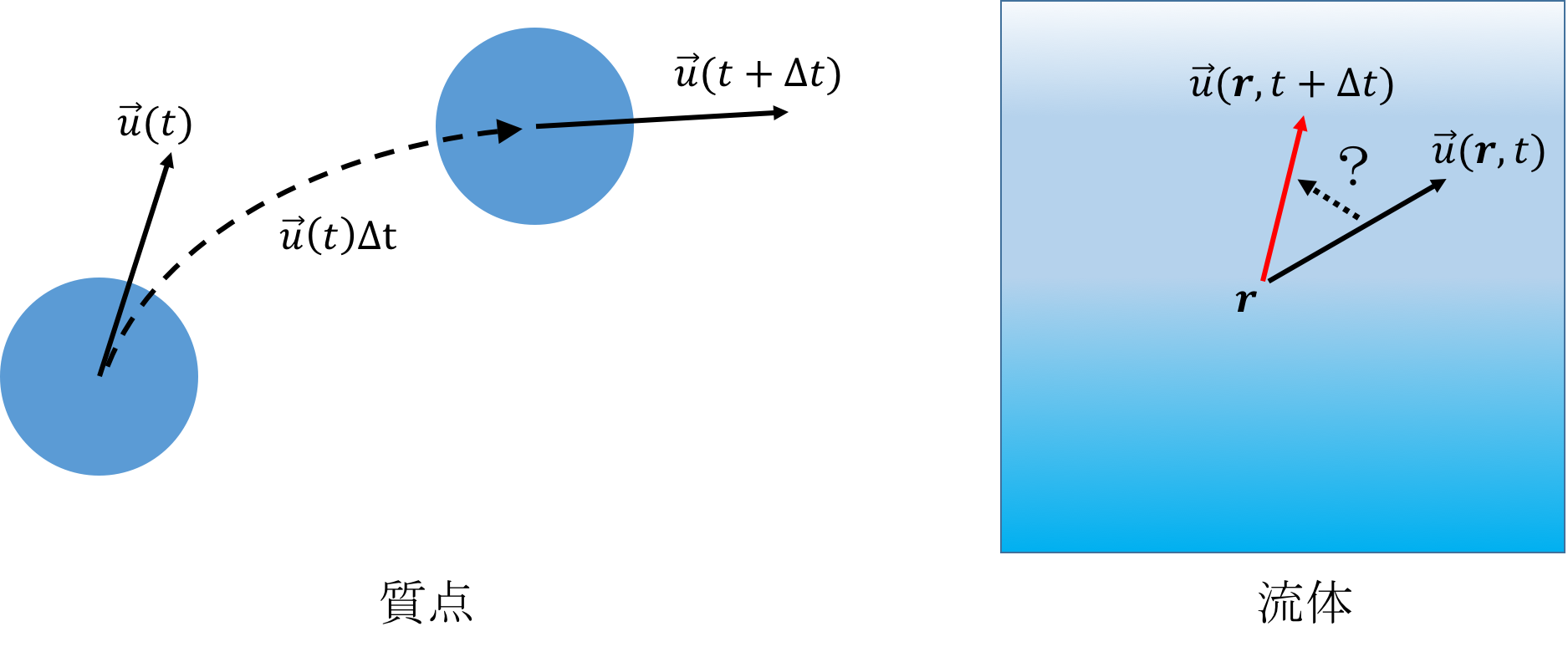
質点の運動では、速度$\vec{u}(t)$というのは常に物体を追いかけているものである($\Delta t$秒後には$\vec{u}(t)\Delta t$だけ移動している)。一方、流体中での速度場$\vec{u}({\bf r},t)$というのは、ある位置${\bf r}$に固定した視点から見た流体速度である。速度場の時間微分は、偏微分$\frac{\partial\vec{u}}{\partial t}$の定義より、
\begin{eqnarray}
\frac{\partial\vec{u}({\bf r},t)}{\partial t} = \lim_{\Delta t \rightarrow 0} \frac{\vec{u}({\bf r},t+\Delta t)-\vec{u}({\bf r},t)}{\Delta t}
\end{eqnarray}
であるが、では$\vec{u}({\bf r},t+\Delta t)$はどのように計算すればよいだろうか。もちろん、これまで見てきたように、圧力勾配や重力によって元の$\vec{u}({\bf r},t)$から微小変化する。しかし、他にも速度場を変化させる要因が存在する。例えば圧力勾配や重力が全く無いような状況を考えてみるとわかりやすい、下図のように左にいくにつれて速度が早くなっているような流体であれば、

時間経過とともに中心位置${\bf r}$での速度$\vec{u}({\bf r},t)$は徐々に大きくなっていくはずである。これは速度場によって位置${\bf r}$の元へ流されて来た、もともとは別の場所にあった速度場$\vec{u}$による更新が行われていることになる(非圧縮性流体では上のような1次元での速度勾配はおそらく発生しない気はするが、とりあえず理解のため)。この流れによる場の量の更新を"移流"による効果と呼び、速度場以外にも密度や温度や色なども移流される。
一般に場の量$\Phi$に対する更新式を導く。位置${\bf r}$へ時刻$t+\Delta t$に到達する$\Phi({\bf r},t+\Delta t)$が求める値である。これを$\Delta t$秒巻き戻して、位置${\bf r}-\vec{u}\Delta t$での値$\Phi({\bf r}-\vec{u}\Delta t,t)$が使えそうである。$\Phi$の時間微分は、
\begin{eqnarray}
\frac{\partial \Phi({\bf r},t)}{\partial t}
&=& \lim_{\Delta t \rightarrow 0} \frac{\Phi({\bf r},t+\Delta t)-\Phi({\bf r},t)}{\Delta t} \\
&=& \lim_{\Delta t \rightarrow 0} \frac{\Phi({\bf r}-\vec{u}\Delta t,t)-\Phi({\bf r},t)}{\Delta t} \\
&=& \lim_{\Delta t \rightarrow 0} \frac{\Phi(x-u_x\Delta t,y-u_y\Delta t,z-u_z\Delta t,t)-\Phi({\bf r},t)}{\Delta t} \\
&\simeq& \lim_{\Delta t \rightarrow 0} \frac{ \left[\Phi({\bf r},t)+\frac{\partial \Phi}{\partial x}(-u_x\Delta t)+\frac{\partial \Phi}{\partial y}(-u_y\Delta t)+\frac{\partial \Phi}{\partial z}(-u_z\Delta t)\right] -\Phi({\bf r},t)}{\Delta t} \\
&=& - \left( u_x \frac{\partial \Phi}{\partial x} + u_y \frac{\partial \Phi}{\partial y} + u_z \frac{\partial \Phi}{\partial z}\right) \\
&=& - (\vec{u} \cdot \nabla) \Phi({\bf r},t)
\end{eqnarray}
つまり、現在の時刻$t$での場の量$\Phi({\bf r},t)$と速度場$\vec{u}({\bf r},t)$から次の時刻での$\Phi({\bf r},t+\Delta t)$を計算することが出来る。
$\Phi$として速度場$\vec v$の3成分$u_x,u_y,u_z$を適用すれば、
\begin{eqnarray}
\frac{\partial\vec{u}({\bf r},t)}{\partial t} = - (\vec{u} \cdot \nabla) \vec{u}({\bf r},t)
\end{eqnarray}
これは移流による速度変化のみを考慮したものなので、圧力項と外力項を追加して式を整理すれば、Navier-Stokes方程式(1)と一致する。
粘性項
(Under consruction...)
数値計算
NS方程式を時間離散化
Staggered格子を用いて空間離散化
C++とOpenGLによる実装
離散化
外力$\vec F_{ext}$を無視する。Navier-Stokes方程式$(1)$を時間$t$について離散化して(時間ステップ$\Delta t$で$t_n\rightarrow t_{n+1}$となるとする)、
\begin{eqnarray}
\frac{\vec{u}_{n+1}-\vec{u}_n}{\Delta t} + (\vec{u}_n\cdot\nabla)\vec{u}_n
= -\frac{1}{\rho}\nabla P_n + \frac{1}{Re} \nabla^2\vec{u}_n
\end{eqnarray}
変形して、
\begin{eqnarray}
\vec{u}_{n+1}
= \vec{u}_n + \Delta t\left[ -(\vec{u}_n\cdot\nabla)\vec{u}_n - \frac{1}{\rho}\nabla P_n + \frac{1}{Re} \nabla^2\vec{u}_n \right]
\end{eqnarray}
これと速度場の発散$0$条件$\nabla \vec{u}_{n+1}=0$を含めて行列表記すると、
\begin{eqnarray}
\begin{pmatrix} I & \nabla \\ \nabla & 0 \end{pmatrix}
\begin{pmatrix} \vec{u}_{n+1} \\ \frac{\Delta t}{\rho} p_n \end{pmatrix}
= \begin{pmatrix} \vec{u}_{n}-\Delta t\left[ (\vec{u}_n\cdot\nabla)\vec{u}_n - \frac{1}{Re} \nabla^2\vec{u}_n \right] \\ 0 \end{pmatrix}
\end{eqnarray}
LU分解して、
\begin{eqnarray}
\begin{pmatrix} I & 0 \\ \nabla & -\nabla\nabla \end{pmatrix}
\begin{pmatrix} I & \nabla \\ 0 & I \end{pmatrix}
\begin{pmatrix} \vec{u}_{n+1} \\ \frac{\Delta t}{\rho} p_n \end{pmatrix}
= \begin{pmatrix} \vec{u}_{n}-\Delta t\left[ (\vec{u}_n\cdot\nabla)\vec{u}_n - \frac{1}{Re} \nabla^2\vec{u}_n \right] \\ 0 \end{pmatrix}
\end{eqnarray}
ここで、中間速度場$\vec{u}^*\equiv\vec{u}_{n+1}+\frac{\Delta t}{\rho}\nabla p$を定義すると、
\begin{eqnarray}
\begin{pmatrix} I & 0 \\ \nabla & -\nabla\nabla \end{pmatrix}
\begin{pmatrix} \vec{u}^* \\ \frac{\Delta t}{\rho} p_n \end{pmatrix}
= \begin{pmatrix} \vec{u}_{n}-\Delta t\left[ (\vec{u}_n\cdot\nabla)\vec{u}_n - \frac{1}{Re} \nabla^2\vec{u}_n \right] \\ 0 \end{pmatrix}
\end{eqnarray}
この行列計算を展開・中間速度場の定義とまとめると、
\left\{
\begin{eqnarray}
\vec{u}^* &=& \vec{u}_{n}-\Delta t\left[ (\vec{u}_n\cdot\nabla)\vec{u}_n - \frac{1}{Re} \nabla^2\vec{u}_n \right] \mathrm{\,\,\,\,\,\,\,\,(2a)} \\
0 &=& \nabla \vec{u}^* - \frac{\Delta t}{\rho} \nabla^2p_n \mathrm{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2b)} \\
\vec{u}_{n+1} &=& \vec{u}^* - \frac{\Delta t}{\rho}\nabla p_n \mathrm{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2c)}
\end{eqnarray} \right. \tag{2}
現在の速度場$\vec u_n$から中間速度場$\vec u^*$が求まり(2a)、中間速度場から圧力場$p_n$を更新する(2b)、圧力勾配から$\vec{u}_{n+1}$が求まる(2c)。(確かに、$\nabla \vec{u}=0$となる。そうなるように(2b)で圧力場$p$を設定したとも言える。)
Staggered格子
Staggered格子を用いる。圧力$p$をセルの真ん中に、速度場$\vec{u}=(u,v)$をセルの辺上に保持する。
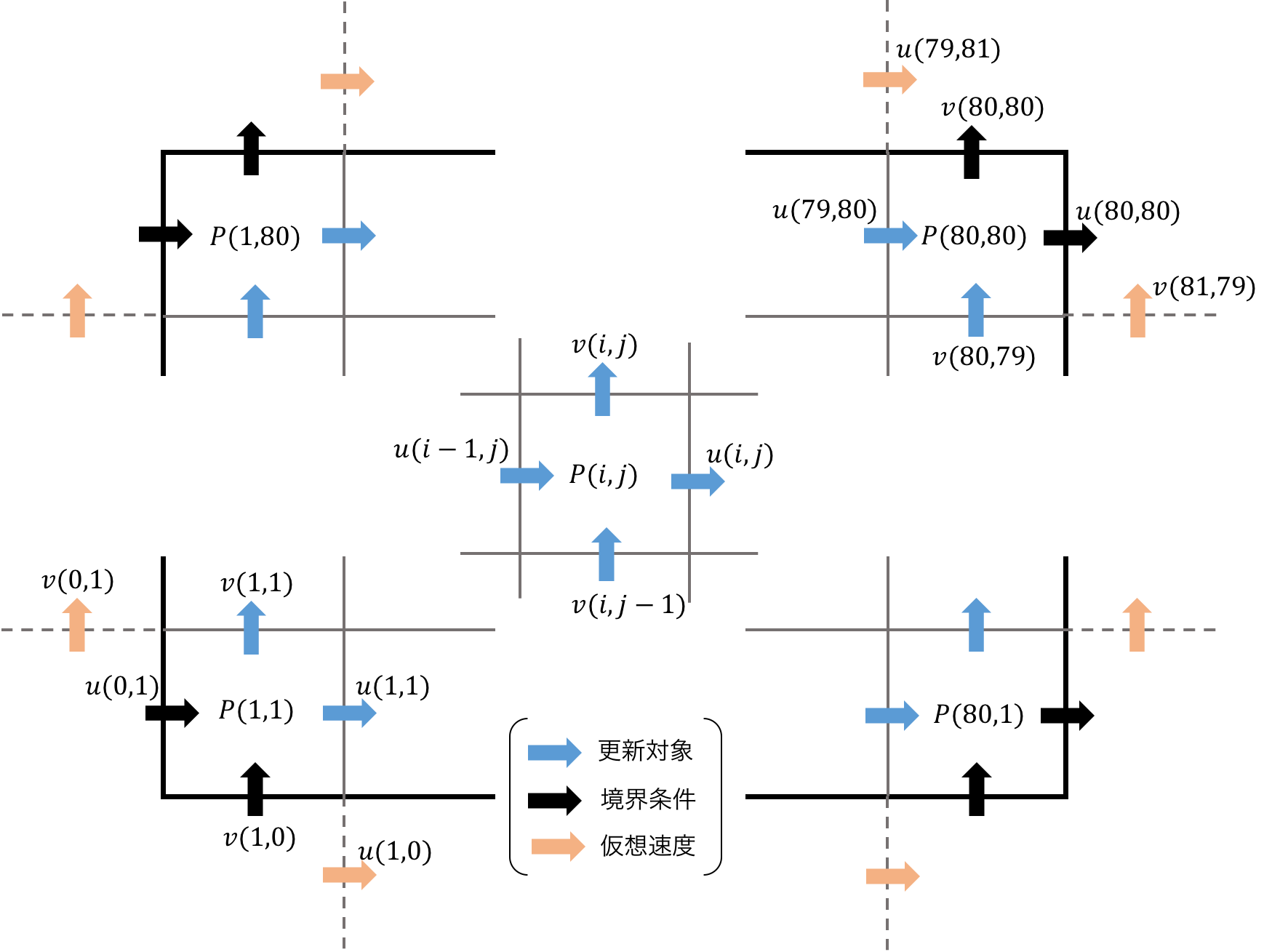
これに基づいて空間離散化を行う。簡単なものから順に示していく。
・式(2c)について、
速度場$u,v$は以下のような圧力勾配を用いて更新すればよい。
\begin{eqnarray}
u(i,j) \leftarrow \frac{\partial p}{\partial x} = \frac{p(i+1,j) - p(i,j)}{\Delta x} \\
v(i,j) \leftarrow \frac{\partial p}{\partial y} = \frac{p(i,j+1) - p(i,j)}{\Delta y}
\end{eqnarray}
・式(2a)の粘性項$\nabla^2 \vec{u}$について、
まず2階微分は定義通り展開して、
\begin{eqnarray}
U''(x) &=& \lim_{\Delta x\rightarrow0} \frac{U'(x+\Delta x)-U'(x)}{\Delta x} \\
&=& \lim_{\Delta x\rightarrow0} \frac{\frac{U(x+\Delta x)-U(x)}{\Delta x}-\frac{U(x)-U(x-\Delta x)}{\Delta x}}{\Delta x} \\
&=& \lim_{\Delta x\rightarrow0} \frac{U(x+\Delta x)-2U(x)+U(x-\Delta x)}{\Delta x^2} \\
\end{eqnarray}
のように離散化する。よって、$\nabla^2 \vec{u}$項は、
\begin{eqnarray}
u^*(i,j) \leftarrow \left(\frac{\partial}{\partial x^2}+\frac{\partial}{\partial y^2}\right) u
&=& \frac{u(i+1,j)-2u(i,j)+u(i-1,j)}{\Delta x^2} + \frac{u(i,j+1)-2u(i,j)+u(i,j-1)}{\Delta y^2} \\
v^*(i,j) \leftarrow \left(\frac{\partial}{\partial x^2}+\frac{\partial}{\partial y^2}\right) v
&=& \frac{v(i+1,j)-2v(i,j)+v(i-1,j)}{\Delta x^2} + \frac{v(i,j+1)-2v(i,j)+v(i,j-1)}{\Delta y^2}
\end{eqnarray}
・式(2a)の移流項について、
移流項$(\vec{u}\cdot\nabla)\vec{u}$は、$\nabla \vec{u}=0$の条件を使えば次のように等価な形に書ける。(そのままでも計算出来そう、CGではSemi-Lagrangian法で計算)
\begin{eqnarray}
(\vec{u}\cdot\nabla)\vec{u}
&=& \left(u\frac{\partial}{\partial x}+v\frac{\partial}{\partial y}\right) \begin{pmatrix} u \\v \end{pmatrix} \\
&=& \begin{pmatrix} u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y} \\ u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y} \end{pmatrix} + \vec u (\nabla \vec{u}) \, (=\vec 0) \\
&=& \begin{pmatrix} 2u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+u\frac{\partial v}{\partial y} \\ u\frac{\partial v}{\partial x}+v\frac{\partial u}{\partial x}+2v\frac{\partial v}{\partial y} \end{pmatrix} \\
&=& \begin{pmatrix} \frac{\partial u^2}{\partial x}+\frac{\partial (uv)}{\partial y} \\ \frac{\partial (uv)}{\partial x}+\frac{\partial v^2}{\partial y} \end{pmatrix}
\end{eqnarray}
ここで、各セルの中央および格子点における速度$u_{cen},u_{cor},v_{cen},v_{cor}$を次の図のように補完することが出来る。(境界の4隅は計算できないが問題ナシ)
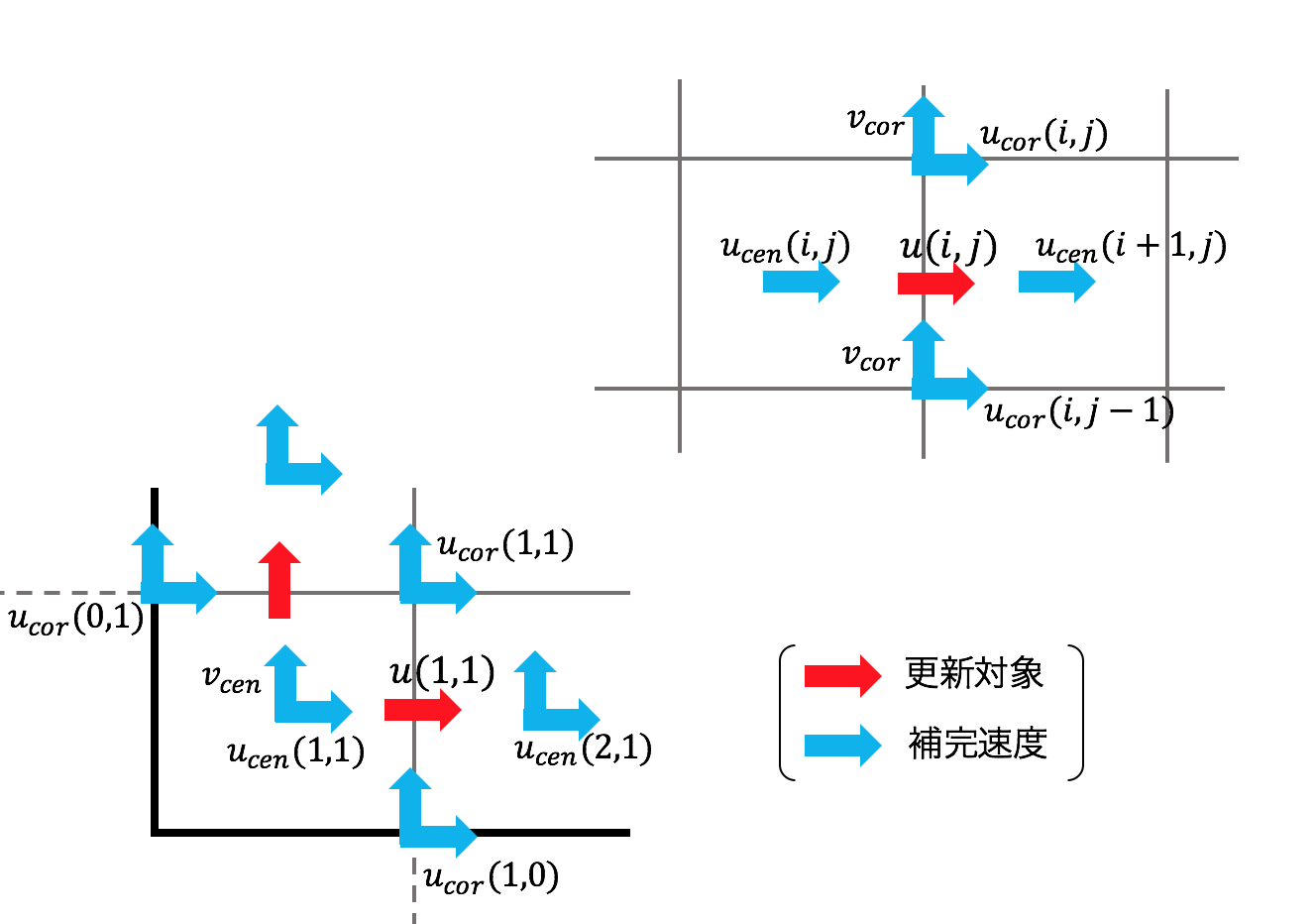
補完値を用いて、
\begin{eqnarray}
\frac{\partial u^2(i,j)}{\partial x} &=& \frac{u_{cen}^2(i+1,j)-u_{cen}^2(i,j)}{\Delta x} \\
\frac{\partial (uv)}{\partial y} &=& \frac{u_{cor}(i,j)v_{cor}(i,j)-u_{cor}(i,j-1)v_{cor}(i,j-1)}{\Delta y} \\
\frac{\partial (uv)}{\partial x} &=& \frac{u_{cor}(i,j)v_{cor}(i,j)-u_{cor}(i-1,j)v_{cor}(i-1,j)}{\Delta x} \\
\frac{\partial v^2(i,j)}{\partial y} &=& \frac{v_{cen}^2(i,j+1)-v
_{cen}^2(i,j)}{\Delta y}
\end{eqnarray}
・式(2b)について、
Poisson方程式を離散化する。($\Delta x = \Delta y$として)
\begin{eqnarray}
\nabla^2p (i,j) &=& \frac{p(i+1,j)-2p(i,j)+p(i-1,j)}{\Delta x^2} + \frac{p(i,j+1)-2p(i,j)+p(i,j-1)}{\Delta y^2} \\
&=& \frac{p(i+1,j)+p(i-1,j)+p(i,j+1)+p(i,j-1)-4p(i,j)}{\Delta x^2}
\end{eqnarray}
境界では圧力勾配が$0$とみなして(Neumann型境界条件)、
\left\{
\begin{eqnarray}
\nabla^2p (1,1) &=& \frac{-2p(1,1)+p(1,2)+p(2,1)}{\Delta x^2} \\
\nabla^2p (1,2) &=& \frac{p(1,1)-3p(1,2)+p(1,3)+p(2,2)}{\Delta x^2} \\
&\vdots& \\
\end{eqnarray}
\right.
行列の形で書くと、
\begin{eqnarray}
\left(
\begin{array}{cccccccc|cccccccc|ccc}
-2 & 1 & 0 & 0 & ... & 0 & 0 & 0 & 1 & 0 & 0 & & ... & & 0 & 0 & 0 & 0 & ... \\
1 & -3 & 1 & 0 & ... & 0 & 0 & 0 & 0 & 1 & 0 & & ... & & 0 & 0 & 0 & 0 & ... \\
0 & 1 & -3 & 1 & ... & 0 & 0 & 0 & 0 & 0 & 1 & & ... & & 0 & 0 & 0 & 0 & ... \\
&\vdots& & \ddots& & & & & & & & & ... & & & & & & ... \\
&\vdots& & &\ddots&& & & & & & & ... & & & & & & ... \\
&\vdots& & & &\ddots& & & & & & & ... & & & & & & ... \\
&\vdots& & & & &\ddots& & & & & & ... & & & & & & ... \\
&\vdots& & & & & & & & & & & ... & & & & & & ... \\
0 & 0 & 0 & 0 & ... & 1 & -3& 1 & 0 & 0 & 0 & & ... & & 1 & 0 & 0 & 0 & ... \\
0 & 0 & 0 & 0 & ... & 0 & 1 & -2 & 0 & 0 & 0 & & ... & & 0 & 1 & 0 & 0 & ... \\
\hline
1 & 0 & 0 & 0 & ... & 0 & 0 & 0 & -3 & 1 & 0 & & ... & & 0 & 0& 1 & 0 & ... \\
0 & 1 & 0 & 0 & ... & 0 & 0 & 0 & 1 & -4 & 1 & & ... & & 0 & 0& 0 & 1 & ... \\
& \vdots \\ & \vdots \\ & \vdots \\ & \vdots \\ \\ \\ \\ \\
\hline
\\
\end{array}
\right)
\left(
\begin{array}{cccccccc|cccccccc|ccc}
p(1,1) \\
p(2,1) \\
p(3,1) \\
\\ \\ \\ \vdots \\ \\ \\
p(79,1) \\
p(80,1) \\
\hline
p(1,2) \\
p(2,2) \\
\\ \\ \\ \vdots \\ \\ \\
p(79,2) \\
p(80,2) \\
\hline
\\
\end{array}
\right)
=
\rho \frac{\Delta x^2}{\Delta t}
\left(
\begin{array}{cccccccc|cccccccc|ccc}
\nabla\vec{u}^*(1,1) \\
\nabla\vec{u}^*(2,1) \\
\nabla\vec{u}^*(3,1) \\
\\ \\ \\ \vdots \\ \\ \\
\nabla\vec{u}^*(79,1) \\
\nabla\vec{u}^*(80,1) \\
\hline
\nabla\vec{u}^*(1,2) \\
\nabla\vec{u}^*(2,2) \\
\\ \\ \\ \vdots \\ \\ \\
\nabla\vec{u}^*(79,2) \\
\nabla\vec{u}^*(80,2) \\
\hline
\\
\end{array}
\right)
\end{eqnarray}
これは巨大対称疎行列$A$についての線形方程式
\begin{equation}
A \vec x = \vec b
\end{equation}
の形になっている。
注意点として、一般に巨大な行列の逆行列を求めることは計算量が非常に大きくなるため、疎行列の性質を使った高速化手法を用いることになる。また、Neumann型境界条件では圧力場$P$について定数分の不定性が残ってしまう(後に速度場を調整するときには微分値のみを使うので辻褄は合うが)。行列の一般的な性質から、解$x$が無数に存在する場合には行列$A$が逆行列を持たない($|A|=0$となり逆行列は発散する)ため、陽に逆行列を数値計算することはできない。今回は初期化時点でQR分解まで行い、後は$x$の解候補1つを自動で選び出してくれるようなsolverを用いた。($x$の1成分を手動で0に固定することでも解決できる?)
実装
・まずは初期条件・配列の宣言を行う。
// 初期値
int n = 80; // 格子分割数
float size = 1.0; // 系のサイズ
float dt = 0.01; // 時間step
float dx = size/n; // 格子サイズ
float Re = 500.0; // Reynolds数
float rho = 1.0; // 密度ρ一定
// 配列の宣言
float P[81][81] = {}; // 圧力P
float u[81][82] = {}; // 速度のx成分
float v[82][81] = {}; // 速度のy成分
float xce[81] = {}; // 座標値
float yce[81] = {};
float x_u[81] = {};
float y_u[82] = {};
float x_v[82] = {};
float y_v[81] = {};
// 境界条件
float bctop = +1.0; // 上面境界に速さ+1.0の流れ
NS方程式による更新部分のみを扱う。
・境界条件を満たすように仮想速度場の計算を行う。
void Time_evolution() {
// 仮想速度場 B.C.
for (int i=1;i<=80;i++) {
u[0][i] = 0.0; // left
u[80][i] = 0.0; // right
v[i][0] = 0.0; // bottom
v[i][80] = 0.0; // top
}
for (int i=1;i<=79;i++) {
v[0][i] = -v[1][i]; // left
v[81][i] = -v[80][i]; // right
u[i][0] = -u[i][1]; // bottom
u[i][81] = 2.0*bctop-u[i][80]; // top
}
}
・移流項による中間速度場を求める (2a)
\begin{eqnarray}
\vec{u}^* &=& \vec{u}_{n}-\Delta t \, (\vec{u}_n\cdot\nabla)\vec{u}_n \\
(\vec{u}\cdot\nabla)\vec{u}
&=& \begin{pmatrix} \frac{\partial u^2}{\partial x}+\frac{\partial (uv)}{\partial y} \\ \frac{\partial (uv)}{\partial x}+\frac{\partial v^2}{\partial y} \end{pmatrix} \\
&=& \frac{1}{\Delta x} \begin{pmatrix} [u_{cen}^2(i+1,j)-u_{cen}^2(i,j)]+[u_{cor}(i,j)v_{cor}(i,j)-u_{cor}(i,j-1)v_{cor}(i,j-1)] \\
[u_{cor}(i,j)v_{cor}(i,j)-u_{cor}(i-1,j)v_{cor}(i-1,j)] + [v_{cen}^2(i,j+1)-v
_{cen}^2(i,j)] \end{pmatrix}
\end{eqnarray}
void Time_evolution() {
// 中間速度場の配列
float u_mid[81][82] = {};
float v_mid[82][81] = {};
// Advection
// -- u_cen と u_vec を補完計算
float u_cen[81][81] = {};
float v_cen[81][81] = {};
float u_cor[81][81] = {};
float v_cor[81][81] = {};
for (int i=1;i<=80;i++) {
for (int j=1;j<=80;j++) {
u_cen[i][j] = (u[i][j]-u[i-1][j])/2.0;
v_cen[i][j] = (v[i][j]-v[i][j-1])/2.0;
}
}
for (int i=0;i<=80;i++) {
for (int j=0;j<=80;j++) {
int temp_flag = (i==0 or i==80) and (j==0 or j==80);
if (!temp_flag) {
u_cor[i][j] = (u[i][j]+u[i][j+1])/2.0;
v_cor[i][j] = (v[i][j]+v[i+1][j])/2.0;
}
}
}
// -- 中間速度場を計算
for(int i=1;i<=79;i++) { // u*
for (int j=1;j<=80;j++) {
float adv_term = 0.0;
adv_term += u_cen[i+1][j]*u_cen[i+1][j] - u_cen[i][j]*u_cen[i][j];
adv_term += u_cor[i][j]*v_cor[i][j] - u_cor[i][j-1]*v_cor[i][j-1];
adv_term /= dx;
u_mid[i][j] = u[i][j] - dt*adv_term;
}
}
for(int i=1;i<=80;i++) { // v*
for (int j=1;j<=79;j++) {
float adv_term = 0.0;
adv_term += v_cen[i][j+1]*v_cen[i][j+1] - v_cen[i][j]*v_cen[i][j];
adv_term += u_cor[i][j]*v_cor[i][j] - u_cor[i-1][j]*v_cor[i-1][j];
adv_term /= dx;
v_mid[i][j] = v[i][j] - dt*adv_term;
}
}
}
・粘性項による中間速度場の更新 (2a)
\begin{eqnarray}
\vec{u}^* &\mathrel{+}=& \frac{\Delta t}{Re} \nabla^2\vec{u}_n \\
\nabla^2\vec{u} &=& \frac{1}{\Delta x^2}
\begin{pmatrix}
[u(i+1,j)-2u(i,j)+u(i-1,j)] + [u(i,j+1)-2u(i,j)+u(i,j-1)] \\
[v(i+1,j)-2v(i,j)+v(i-1,j)] + [v(i,j+1)-2v(i,j)+v(i,j-1)]
\end{pmatrix}
\end{eqnarray}
void Time_evolution() {
// Viscosity
float Lu[80][81] = {};
float Lv[81][80] = {};
for(int i=1;i<=79;i++) { // x成分
for (int j=1;j<=80;j++) {
float Lu = (u[i+1][j]-2.0*u[i][j]+u[i-1][j])/(dx*dx) + (u[i][j+1]-2.0*u[i][j]+u[i][j-1])/(dx*dx);
u_mid[i][j] += dt/Re*Lu;
}
}
for(int i=1;i<=80;i++) { // y成分
for (int j=1;j<=79;j++) {
float Lv = (v[i+1][j]-2.0*v[i][j]+v[i-1][j])/(dx*dx) + (v[i][j+1]-2.0*v[i][j]+v[i][j-1])/(dx*dx);
v_mid[i][j] += dt/Re*Lv;
}
}
}
・Poisson方程式による圧力項の決定 (2b)
\begin{eqnarray}
\frac{\Delta t}{\rho} \nabla^2p_n &=& \nabla \vec{u}^* \\
A \vec{x} &=& \vec{b}
\end{eqnarray}
行列計算にはEigenモジュールを使用する。巨大疎行列$A$を作成する。
// Eigen
# include <Eigen/Sparse>
# include <Eigen/Dense>
# include <Eigen/SparseQR>
# include <Eigen/IterativeLinearSolvers>
using namespace Eigen;
typedef Eigen::Triplet<double> T;
// 初期化
void Init() {
// 疎行列Aを作成する
vector<T> V;
int size = 80;
for (int i=0;i<size;i++) {
for (int j=0;j<size;j++) { // (i,j)
int k = i+j*size;
if ((i==0 or i==size-1) and (j==0 or j==size-1)) { // 4隅
V.push_back( T(k,k,-2.0) );
if (i==0) {V.push_back( T(k,k+1,1.0) );}
else {V.push_back( T(k,k-1,1.0) );}
if (j==0) {V.push_back( T(k,k+size,1.0) );}
else {V.push_back( T(k,k-size,1.0) );}
}
else if ((i==0 or i==size-1) or (j==0 or j==size-1)) { // 辺
V.push_back( T(k,k,-3.0) );
int temp[4] = {k-1,k+1,k-size,k+size};
int temp_a[4] = {i-1,i+1,j-1,j+1};
for (int l=0;l<4;l++) {
if (temp_a[l]>=0 and temp_a[l]<=size-1) {
V.push_back( T(k,temp[l],1.0) );
}
}
}
else { // 中
V.push_back( T(k,k,-4.0) );
V.push_back( T(k,k+1,1.0) );
V.push_back( T(k,k-1,1.0) );
V.push_back( T(k,k+size,1.0) );
V.push_back( T(k,k-size,1.0) );
}
}
}
A.setFromTriplets(V.begin(), V.end());
//cout << A.topLeftCorner(85, 85) << endl;
solver.compute(A); // QR decomposition !80秒程かかる
}
初期化時点で$A$をQR分解まで行っている。これには80秒程かかる。より高速なiterative手法ConjugateGradientを試したらダメだったのでとりあえずdirect手法を使用した。
solverに$\nabla \vec{u}^*$ベクトルを投げる。係数部分を調整して、圧力場$P$を求める。
void Time_evolution() {
// Pressure (Poisson eq Ax=b)
// ベクトルbを作成
VectorXd b(n*n);
for (int i=0;i<80;i++) {
for (int j=0;j<80;j++) {
b(i+j*80) = (u_mid[i+1][j+1]-u_mid[i][j+1])/dx + (v_mid[i+1][j+1]-v_mid[i+1][j])/dx;
}
}
// solverにAとbを投げる
VectorXd x;
x = solver.solve(b);
// 圧力場Pに代入する
float coeff = rho*dx*dx/dt;
for (int i=0;i<80;i++) {
for (int j=0;j<80;j++) {
P[i+1][j+1] = coeff*x(i+j*80);
}
}
}
・圧力勾配から速度場を更新する (2c)
\begin{eqnarray}
\vec{u}_{n+1} &=& \vec{u}^* - \frac{\Delta t}{\rho}\nabla p_n \\
\nabla p &=& \frac{1}{\Delta x}
\begin{pmatrix} p(i+1,j) - p(i,j) \\ p(i,j+1) - p(i,j) \end{pmatrix}
\end{eqnarray}
void Time_evolution() {
// ∇P
for(int i=1;i<=79;i++) {
for (int j=1;j<=80;j++) {
float Gp = (P[i+1][j]-P[i][j])/dx;
u[i][j] = u_mid[i][j] - dt/rho*Gp;
}
}
for(int i=1;i<=80;i++) {
for (int j=1;j<=79;j++) {
float Gp = (P[i][j+1]-P[i][j])/dx;
v[i][j] = v_mid[i][j] - dt/rho*Gp;
}
}
}
速度場がきちんと発散$0$になっているか確認する。
\begin{eqnarray}
\nabla \vec{u} = 0
\end{eqnarray}
void Time_evolution() {
// ∇u=0
float div = 0.0;
for (int j=80;j>=1;j--) {
for (int i=1;i<=80;i++) {
float temp = (u[i][j]-u[i-1][j])/dx + (v[i][j]-v[i][j-1])/dx;
if(abs(temp)>0.001) {
cout << int(temp) << " ";
}
else cout << 0 << " ";
}
cout << endl;
}
}
(自分用コメント) 渦度の大きいような初期条件でのシミュレーションでは直角状のartifactが発生するが、これは移流項を差分化により計算したことで起こるようである(シミュレーション全体を45度回転させて動かしても同様に直角の流れが発生するのでartifactであることが確認出来る)。Semi-Lagrangian法を使うと解決する。