これまでというもの,ベイズ推定についてはふわっとしか理解していなかったので,コイントスの具体例を使って逐次ベイズ推定が何なのかをしっかり理解し,コイントスを実際に逐次ベイズ推定していきます.
記号が分かりにくいベイズの定理
ベイズ推定というと以下の式("更新式"とする)が有名ですが
p(\theta;D)=\frac{p(\theta) p(D;\theta)}{p(D)}
まずはそもそもベイズの定理が何を目指しているのか確認します.その後,似通った記号が出てきて紛らわしいので,それぞれの意味の違いを明確にし差別化を図ります.
何を目指しているのか
ベイズの定理の目標は,$\theta$の真の値を求めることです.$\theta$は,ここでは"コインの表が出る確率"とします.
ベイズの定理の中では,$\theta$の値は確率分布で表されます.「$\theta=0.5$である確率は50%,$\theta=0.7$である確率は20%かな〜」みたいな感じです.どうやって$\theta$の真の値を求めるかというと,実現値を得ながら,更新式を繰り返し行うことで(逐次ベイズ推定),$\theta$の確率分布を鋭くします.
具体的には,$n$ステップ目でコインを1回投げて,表裏に関する実現値$x_i$を得る.更新式を繰り返して,コインの表が出る 確率$\theta$の確率分布(!?!?) を先鋭化させていきます.
ベイズ推定では,コインの表が出る確率の確率分布を扱います.この言い回しが,ベイズ推定の難しいところだと思います.
記号を差別化する
例で紹介しているコイントスで説明しやすいように,更新式を以下のように書き換えます.
p(\theta;D_n)=\frac{p(\theta;D_{n-1}) p(x_n;\theta)}{C}
- 実現値$x_i={0,1}$.裏が出たら0,表が出たら1とします.
- パラメータ$\theta\in[0,1]$.表が出る確率とします.
- これまでの実現値$D_n=[x_1,\dots,x_n]$
$n$ステップ目における
| 記号 | 説明 | 以下からはこう表します |
|---|---|---|
| $p(\theta;D_n)$ | 実現値$x_n$が追加された後の時点での,パラメータの真の値が$\theta$である確率 | パラメータ分布paramdist_n,事後パラメータ分布posterior_n
|
| $p(\theta;D_{n-1})$ | 実現値$x_n$が追加される前の時点での,パラメータの真の値が$\theta$である確率 | パラメータ分布paramdist_n-1,事前パラメータ分布prior_n
|
| $p(x_n;\theta)$ | 実現値$x_n$が与えられた時の,$\theta$の尤度 | 尤度関数lh_n
|
| $C$ |
posterior_nの全ての$\theta$における積分が1になるように設定する正規化定数. |
新しい表現形式で更新式を書くと,
\mathtt{paramdist_n}=
\frac{
\mathtt{paramdist_{n-1}} ~ \mathtt{lh_n}
}{
C
}
あるいは
\mathtt{posterior_n}=
\frac{
\mathtt{prior_n} ~ \mathtt{lh_n}
}{
C
}
となります.
また,事後パラメータ分布posterior_nは,次のステップの事前パラメータ分布prior_n+1となります.こうしてステップを重ねると共にパラメータ分布が加工されていきます.
Step by Stepで逐次ベイズ推定
ここからはSympyを使って,パラメータ分布がどう変わっていくかを具体的に見ながら,コイントスを逐次ベイズ推定していきます.
import sympy as sp
theta = sp.var("theta")
x = sp.var("x")
最初に決めておくもの
初期設定として我々が決めておくものは2つあります.
❶ $p$の原型
$p$はparamdistとlhに派生する元となる確率関数です.表が出る確率を$\theta$で表します.$x=1$となる確率は$\theta$,$x=0$となる確率は$1-\theta$なので,
p_func_base = theta*x + (1-theta)*(1-x)
と設定しておきます.p_func_baseは$x,\theta$の2値関数です.
❷ 最初のパラメータ分布
$n=1$ステップ目における事前パラメータ分布paramdist_0を
paramdist_0 = 1+0*theta
という一様分布とします.
1ステップ目
1ステップ目でコインを投げたところ,裏が出たとします.実現値は$0$なので.
# 1ステップ目
x1 = 0
この実現値に対する尤度関数を出すと
lh_1 = p_func_base.subs(x,x1)
1−θ
$\theta=0$の時に最も大きくなる関数です.「コインの裏が出る尤もらしさは$1$,表が出る尤もらしさは$0$」って言っています.
ここから更新式を用いて事後パラメータ分布を求めます.
paramdist_1 = paramdist_0 * lh_1
paramdist_1/= paramdist_1.integrate((theta,0,1))
paramdist_1
2−2θ
$\theta=0$の時に最も大きくなる分布です.「これまでの実現値を見るに,$\theta=0$である確率が高いね」って言っています.
2ステップ目
2ステップ目でコインを投げたところ,表が出たとします.実現値$=1$に対する尤度関数を出すと
# 2ステップ目
x2 = 1
lh_2 = p_func_base.subs(x,x2)
lh_2
θ
$\theta=1$の時に最も大きくなる関数です.「コインの裏が出る尤もらしさは$0$,表が出る尤もらしさは$1$」って言っています.って言っています.
ここから更新式を用いて事後パラメータ分布を求めます.
paramdist_2 = paramdist_1 * lh_2
paramdist_2/= paramdist_2.integrate((theta,0,1))
paramdist_2
3θ(2−2θ)
ちょっと複雑になったので,ここでそれぞれの分布をグラフで見ます.
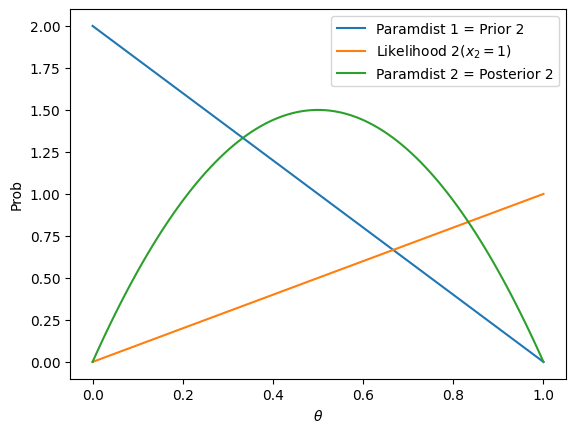
$\theta=0$になる確率が高いと思っていた(青線)んだけど,表が出たという実現値を得たので(オレンジ線),$\theta=0.5$辺りになる確率が高いのかな〜と考えを改めた(緑線)っていう感じです.
3ステップ目
表が出たとして,事後パラメータ分布を求めると
# 3ステップ目
x3 = 1
lh_3 = p_func_base.subs(x,x3)
paramdist_3 = paramdist_2 * lh_3
paramdist_3/= paramdist_3.integrate(paramdist_normalizer)
paramdist_3 = paramdist_3.simplify()
paramdist_3
12θ^2⋅(1−θ)
段々次数が上がっていく・・・
以下の図は,それぞれのステップにおけるパラメータ分布を示しています.
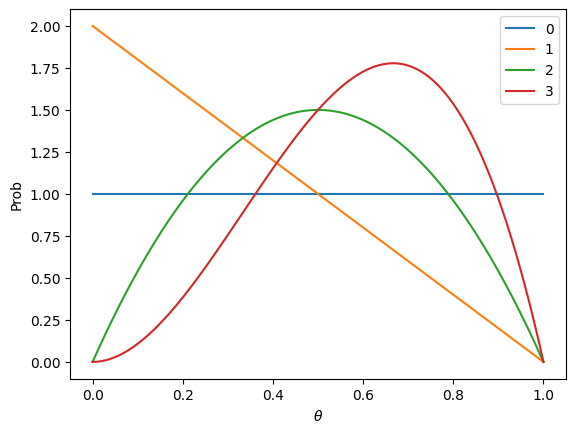
ステップを重ねるごとにグラフが先鋭化していくのが分かります.このグラフはコインの表が出る確率の確率分布を表していますので,これは,実現値を繰り返し貰うことにより,コインの表が出る確率に対する自信が上がってきたと言うことができます.
何回もループする
以上のセクションで逐次行っていた処理を自動化して,何回もループするようにしました.
以下のように実現値を100個用意し,表が出る確率を70%としました.
1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1,
0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0,
1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1,
1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1,
1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0
つまり,これに対して逐次ベイズ推定すれば,$\theta=0.7$にピークを持った鋭いパラメータ分布が出来上がるはずです.
結果として,ステップが進むにつれて,パラメータ分布が先鋭化していくのが見られました!!
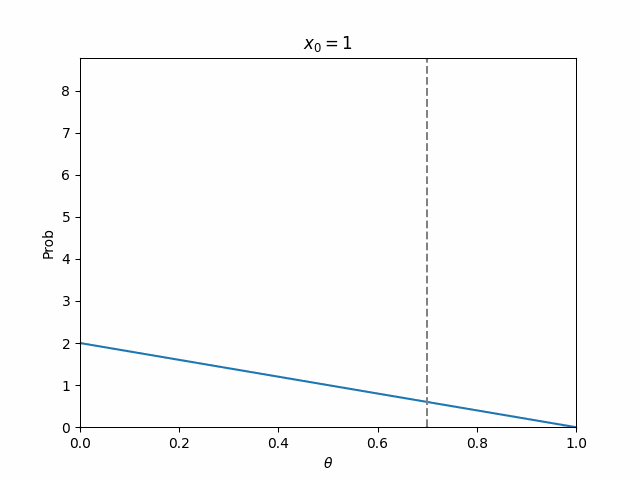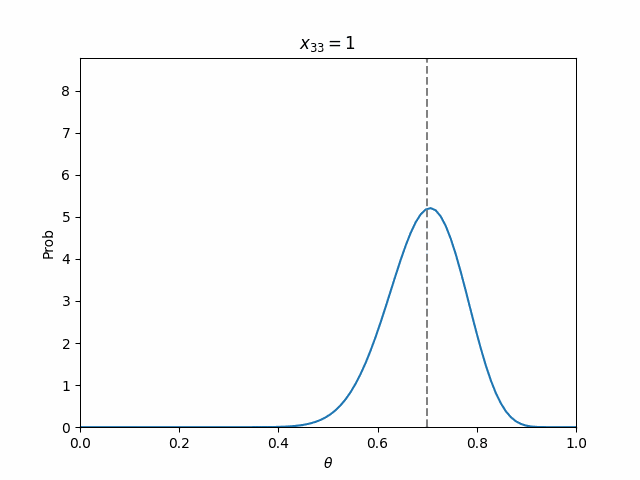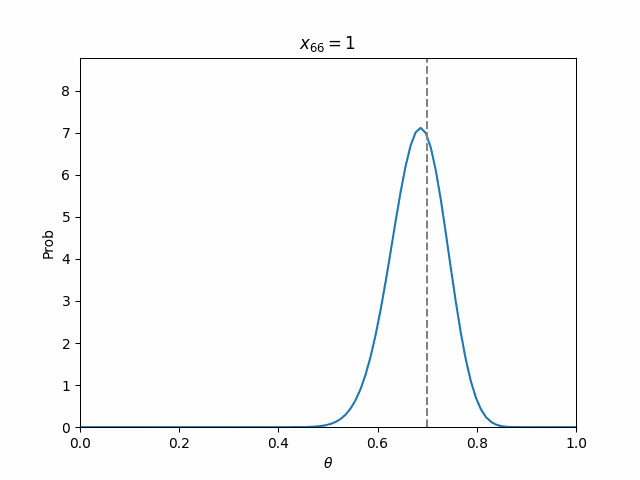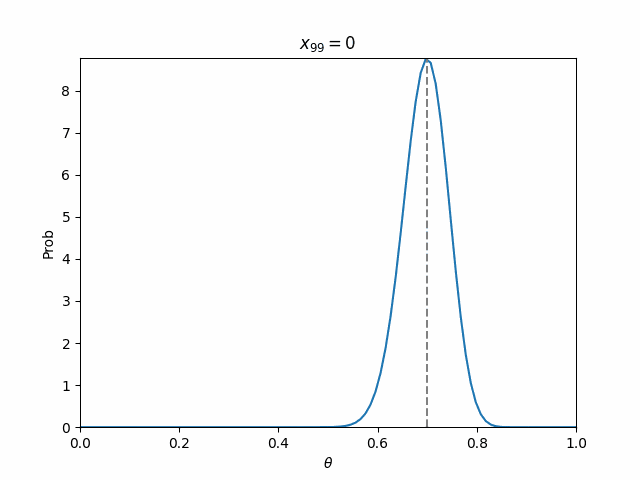
ちなみに,最終的なパラメータ分布は
4880545884552192799620558960\theta^{70}(1−\theta)^{30}(2−2\theta)
となりました.えぐい.
※初期のパラメータ分布を$2-2\theta$としていたので,$\theta$についての$1+100=101$次式になっています.
Tips : Sympy高速化
今回はSympyでパラメータ分布や尤度関数を作り,そこの$\theta$に$[0,1]$の値を代入しながらグラフを作成していきました.この時,以下のような書き方だと
theta_val_s = np.linspace(0,1,100)
p_val_s = np.array([ sympy_expr.subs(theta, theta_val) for theta_val in theta_val_s ])
めっちゃ遅いです.
そんな時に使えるのがlambdifyというものです.これは,値代入がめっちゃ速いSympyの数式オブジェクトを作るものです.
theta_val_s = np.linspace(0,1,100)
lambda_func = sympy.lambdify(theta,sympy_expr,"numpy")
p_val_s = lambda_func(theta_val_s)
.MATLABでいうmatlabFunctionと同じですね.