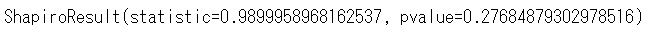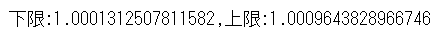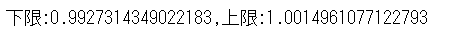投資において、株式のリターンを正規分布と考えることが多いですが、Pythonと機械学習を使うことで、実際にはどのような分布になっているかを考察してみます。
Python、機械学習、株の話ですが、そこまで難しい内容までは踏み込まないので気軽に読んでもらえればと思います。
背景
投資の教科書として有名な「ウォール街のランダム・ウォーカー」では、現在の株価には、利用可能なすべての情報が織り込まれているので、予測は不可能というランダム・ウォーク理論が紹介されています。ランダム・ウォーク理論においては、リスクを考えることが重要になります。金融資産におけるリスクとは、リターンの標準偏差のことです。
効率的市場理論は、相場はランダム・ウォークすると主張する。
多数のプロがより高いリターンを上げようとする結果、すべての新しい材料がたちどころに個別銘柄の株価に織り込まれる。したがって、魅力的な銘柄を選び当て、あるいは市場全体の先行きを予測できる確率は、よくて五分五分なのである。
(中略)
リスクこそ、そしてリスクのみが、どの銘柄のリターンがどの程度市場平均を上回るのかを決め、株式の価値を決めるのだ。
「ウォール街のランダム・ウォーカー」でも勧められているインデックス投資では、期待リターンがプラスで、できるだけリスクの小さいものを長期で保有するという戦略をとります。つまり、リターンの分布を理解することが重要になります。本記事では、株価のリターンについて分析を行います。
使用するライブラリ
# データ読み込み
import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from scipy.stats import norm
import seaborn as sns
from scipy.stats import t
from scipy import stats
from sklearn.preprocessing import StandardScaler
from sklearn.svm import OneClassSVM
使用するデータ
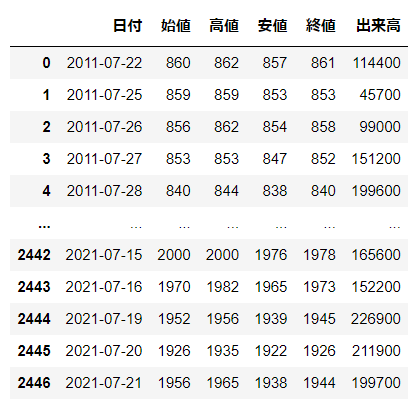
データは何でもよいですが、上場インデックスファンドTOPIX(1308)の2011/7/22~2021/7/21のデータを使用します。
## データの確認
file = 'data/FTOPIX.xlsx'
df = pd.read_excel(file)
df
前日比率の計算
- 出来高データは今回は使わないので削除
- .shift()を使い1日ずれたデータを作成し前日比率を計算
# 出来高は不要なので削除
del df['出来高']
# 1日ずらした列を作成
for i in ['始値', '高値', '安値', '終値']:
df[i + "(前日)"] = df[i].shift(1)
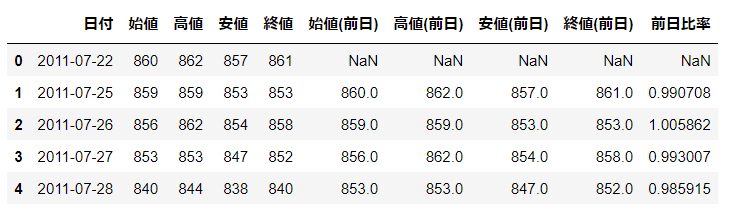
# 前日比率を計算
df['前日比率'] = df['終値'] / df['終値(前日)']
df.head()
ボラティリティを計算
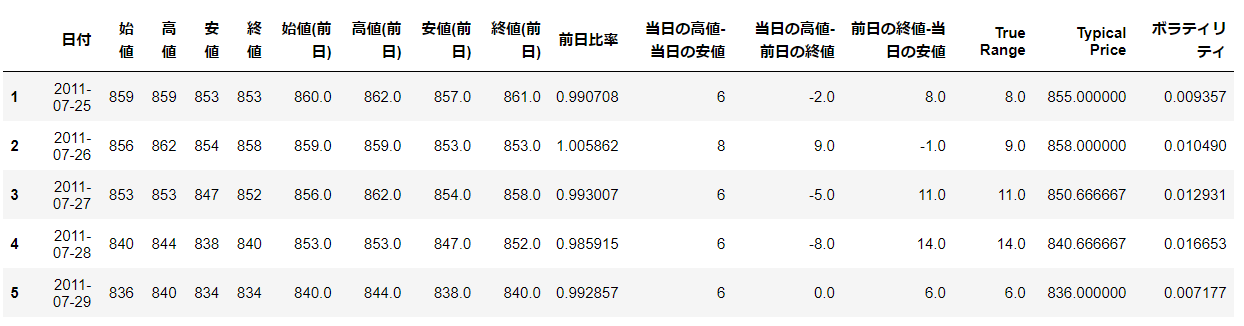
ボラティリティはTrue RangeとTypical Priceから計算します。細かい説明はしませんが、ボラティリティは資産価格の変動の大きさを表すパラメータだと考えてもらえればいいです。
# True Rangeの計算
df['当日の高値-当日の安値'] = df['高値'] - df['安値']
df['当日の高値-前日の終値'] = df['高値'] - df['終値(前日)']
df['前日の終値-当日の安値'] = df['終値(前日)'] - df['安値']
df['True Range'] = df[['当日の高値-当日の安値', '当日の高値-前日の終値',
'前日の終値-当日の安値']].max(axis = 1)
# Typical Priceの計算
df['Typical Price'] = (df['高値'] + df['安値'] + df['終値']) / 3
# ボラティリティの計算
df['ボラティリティ'] = df['True Range'] / df['Typical Price']
# 欠損処理
df = df.dropna()
df.head()
必要な列のみ抽出
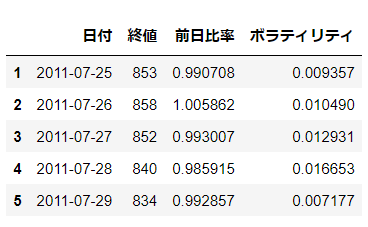
分析に使用するのは4列のみなので、そこだけ抽出しておきます。これでデータが完成です!
df = df[['日付', '終値', '前日比率', 'ボラティリティ']]
df.head()
時系列データとボラティリティの可視化
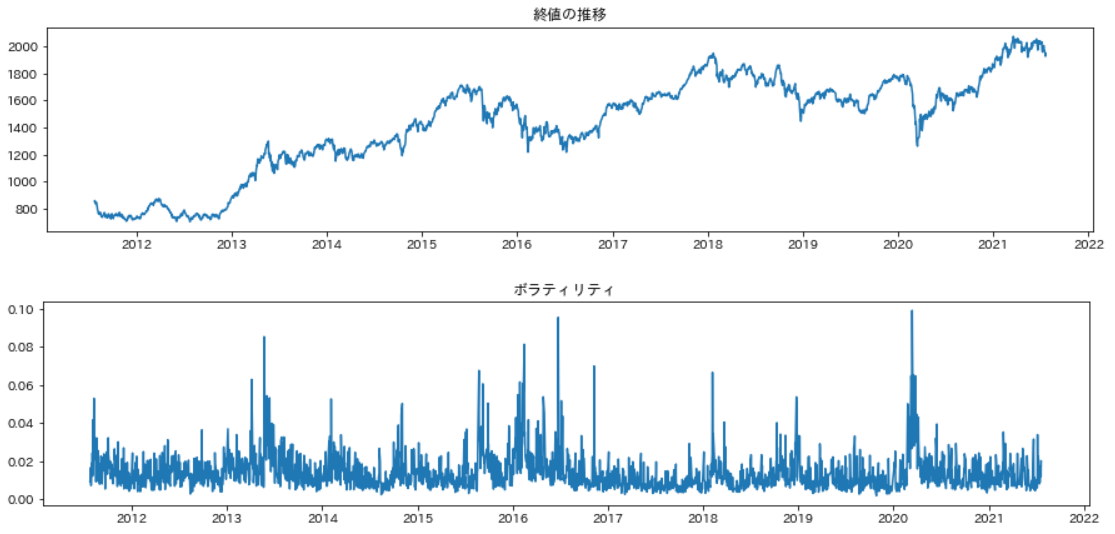
グラフにして、可視化してみます。変動が大きいところでボラティリティが大きくなっていることがわかります。
# グラフ化
plt.figure(figsize = (15, 3))
plt.plot(df['日付'], df['終値'])
plt.title('終値の推移')
plt.show()
plt.figure(figsize = (15, 3))
plt.plot(df['日付'], df['ボラティリティ'])
plt.title('ボラティリティ')
plt.show()
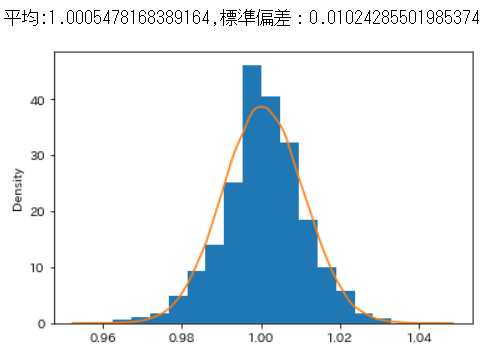
リターンの分布の確認
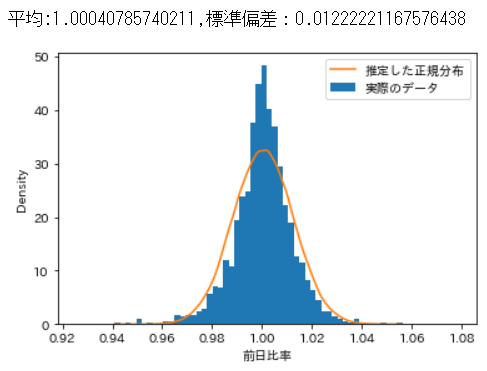
ではここで、株のリターン(前日比率)がどういう分布になっているかを見てみます。今回計算した実際の株のデータをヒストグラムにし、その上に、推定で求めた正規分布を重ねています。グラフを見てみると、正規分布よりもとがった分布になっていることが分かります。
# 前日比率データからヒストグラムを作成
plt.hist(df['前日比率'], bins = 70, density = True, label = '実際のデータ')
# 正規分布を推定
loc, scale = norm.fit(df['前日比率'])
print('平均:{},標準偏差:{}'.format(loc, scale))
# 推定した結果で分布を作成し、可視化
sample = np.random.normal(loc, scale, 100000)
sns.kdeplot(sample, label = '推定した正規分布')
plt.xlabel('前日比率')
plt.legend()
plt.show()
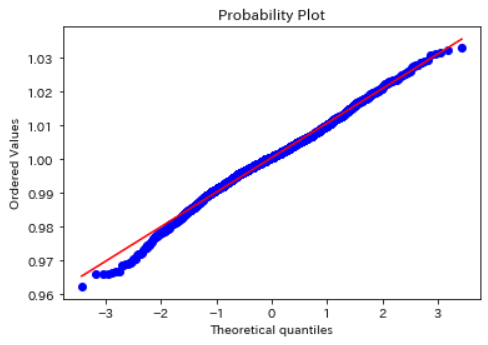
正規性の確認
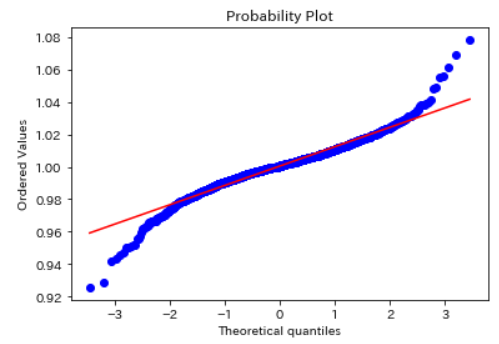
q-qプロットを使うと、データが正規分布しているかどうかを確認することができます。直線になっていれば、正規分布です。今回は直線になっていないので、正規分布ではないことが分かります。
# q-qプロットを確認すると、正規分布していないことがわかる
stats.probplot(df['前日比率'].dropna(), dist = "norm", plot = plt)
plt.show()
考察
ここまでで、株のリターン(前日比率)は正規分布していないことが分かりました。
投資においてはよく、ボラティリティが高い状態と低い状態を分けて考えます。そこで今回、ボラティリティを使ってデータを正常状態と異常状態に分けてみます。そして正常状態と異常状態を分けた状態では、正規分布になっていると仮説を立てて検証を進めてみます。
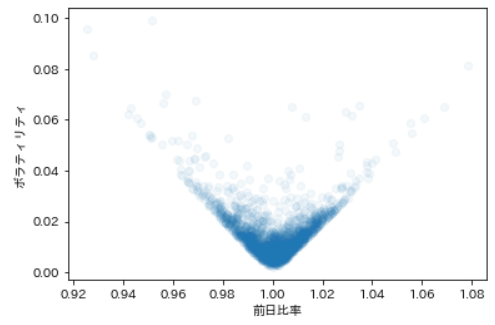
まず参考にボラティリティと前日比率の関係性をグラフ化します。ボラティリティが高いほど、前日比率が散らばっていくのが分かります。
# ボラティリティと前日比率の関係性
plt.scatter(df['前日比率'], df['ボラティリティ'], alpha = 0.05)
plt.xlabel('前日比率')
plt.ylabel('ボラティリティ')
plt.show()
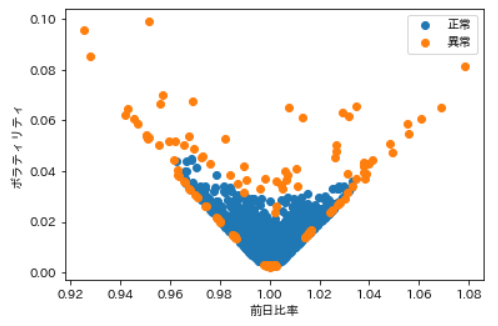
OneClassSVMによる正常・異常の分割
ではここから、正常状態と異常状態に分けていきます。 ここでは正規化をしてくれるStandardScalerと、教師無し学習のOneClassSVMという手法を使用します。正規化というのは、前日比率とボラティリティのスケールを合わせるために行っています。OneClassSVMの原理については割愛しますが、データを与えると、いい感じに正常と異常に分けてくれる手法と考えてもらえれば良いです。
今回は異常状態が5%あると仮定しています。
# 正規化を実施
X_train = df[['前日比率', 'ボラティリティ']]
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
# one class svmでデータを正常・異常に分ける
clf = OneClassSVM(nu = 0.05, kernel = 'rbf', gamma = 0.5)
clf.fit(X_train_std)
pred = clf.predict(X_train_std)
X_train['svm'] = pred
# 結果を可視化
for i in [1, -1]:
temp = X_train[X_train['svm'] == i]
plt.scatter(temp['前日比率'], temp['ボラティリティ'])
plt.legend(['正常', '異常'])
plt.xlabel('前日比率')
plt.ylabel('ボラティリティ')
plt.show()
機械学習を使うことで、あまり深く考えずに、正常と異常を分けることができました!
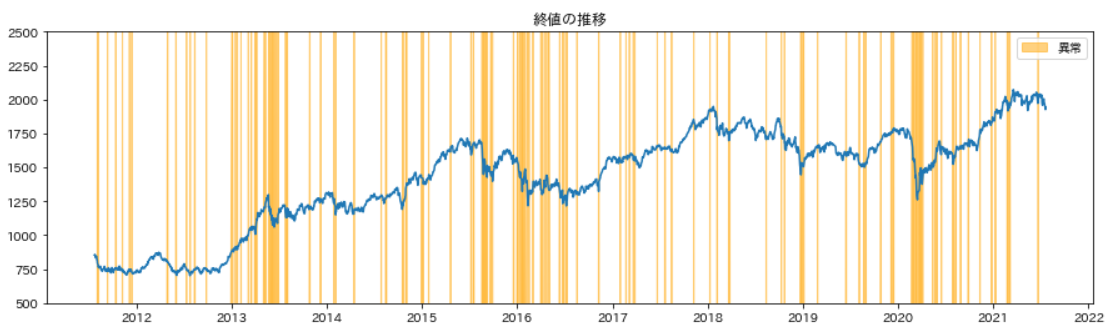
また、異常状態を、時系列データに重ねると以下のようになります。
異常が集中するエリアでは株価が急落していることが分かります。
# 異常時の株価の推移
plt.figure(figsize = (15, 4))
plt.plot(df['日付'], df['終値'])
plt.title('終値の推移')
plt.fill_between(df['日付'], -100, (-X_train['svm'] + 1) * 2000, color = "orange", alpha = 0.5, label = '異常')
plt.ylim(500, 2500)
plt.legend()
正常データの正規性の確認
正常データのみで、正規性を確認してみます。かなり直線に近づいており、おおよそ正規分布していそうです。
# 正常データのみ抽出
df_temp_1 = X_train[X_train['svm'] == 1]
# q-qplot
stats.probplot(df_temp_1['前日比率'].dropna(), dist = "norm", plot = plt)
plt.show()
分布を確認すると以下のようになります。
正常状態においては、平均の前日比率は1を超えているので、期待リターンはややプラスということが分かります。
plt.hist(df_temp_1['前日比率'], bins = 15, density = True)
loc1, scale1 = norm.fit(df_temp_1['前日比率'].dropna())
print('平均:{},標準偏差:{}'.format(loc1, scale1))
sample_1 = np.random.normal(loc1, scale1, 100000)
sns.kdeplot(sample_1)
plt.show()
異常データの正規性の確認
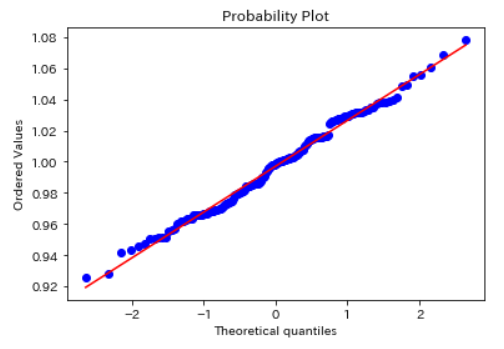
同様に異常データのみで、正規性を確認してみます。かなり直線に近いです。
df_temp_2 = X_train[X_train['svm'] == -1]
stats.probplot(df_temp_2['前日比率'].dropna(), dist = "norm", plot = plt)
plt.show()
ここで、異常データは1000件以下なので、シャピロー・ウィルク検定を行ってみます。シャピロー・ウィルク検定では、正規分布をしていなければ、pvalueが0.05以下になります。
pvalueは0.277となり、正規分布していると言ってよいと思います。
stats.shapiro(df_temp_2['前日比率'])
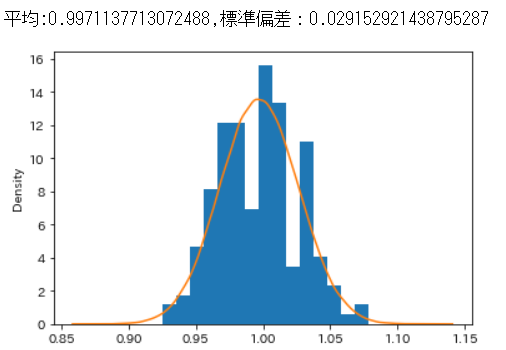
これまでと同じように分布も確認しておきます。
異常時は、前日比率の平均は1を下回り、標準偏差は正常時の3倍近くあることが分かります。これは、異常時は株の値動きが大きく、下落の可能性が高いことを表しています。
sample_2 = np.random.normal(loc2, scale2, 100000)
loc2, scale2 = norm.fit(df_temp_2['前日比率'].dropna())
print('平均:{},標準偏差:{}'.format(loc2, scale2))
plt.hist(df_temp_2['前日比率'], bins=15, density=True)
sns.kdeplot(sample_2)
plt.show()
リターンの区間推定
正常時のリターンを信頼区間95%で区間推定してみると、下限であっても1を超えていることが分かります。つまり、正常時に株を持っていた場合95%の確率で期待リターンはプラスということになります。
# 母分散
sigma2 = scale1**2
# 標本サイズ
n = len(df_temp_1)
# 標本平均
sample_mean = loc1
# 標準正規分布の上側2.5%点
p_975 = t.ppf(0.975, len(df_temp_1) - 1)
# 信頼区間
x_0 = sample_mean - (p_975 * (np.sqrt(sigma2 / n)))
x_1 = sample_mean + (p_975 * (np.sqrt(sigma2 / n)))
print('下限:{},上限:{}'.format(x_0, x_1))
異常時の場合は、以下のようになります。
sigma2 = scale2**2
n = len(df_temp_2)
sample_mean = loc2
z_a = stats.norm.ppf(scale = 1, loc = 0, q = 0.975)
x_0 = sample_mean - (z_a * (np.sqrt(sigma2 / n)))
x_1 = sample_mean + (z_a * (np.sqrt(sigma2 / n)))
print('下限:{},上限:{}'.format(x_0, x_1))
まとめ
ということで、長かったですが分析結果をまとめます。
- 株価のリターン(前日比率)の分布についての分析を行った
- 株価のリターンは正規分布はしていない
- 全データの5%を異常、95%を正常と仮定し、OneClassSVMで正常状態と異常状態に分けることで、それぞれの状態内では正規分布していることが確認できた
- 正常状態ではリターンの平均値はプラスだが、異常状態ではリターンの平均値がマイナスになり、標準偏差も3倍となる
この結果を踏まえたシミュレーションについては、また今後投稿していきます。