【dqn】カオスな運動を深層強化学習する♬～たぶん過誤。。。

いよいよカオスな運動を深層強化学習してみました。

やったこと

（１）Pendulumの深層強化学習
（２）カオスなDuffing振動子の深層強化学習
（３）カオスなLorenz方程式の解の深層強化学習
（４）ちょっと考察

（１）Pendulumの深層強化学習

※コードは見出しからリンクしてます

Training for 9600 steps ...
Interval 1 (0 steps performed)
 9600/10000 [===========================>..] - ETA: 5s - reward: 67.6096done, took 135.389 seconds
Testing for 5 episodes ...
Episode 1: reward: 34889.989, steps: 240
Episode 2: reward: 34889.989, steps: 240
Episode 3: reward: 34889.989, steps: 240
Episode 4: reward: 34889.989, steps: 240
Episode 5: reward: 34889.989, steps: 240
Testing for 10 episodes ...
Episode 1: reward: 34889.989, steps: 240
Episode 2: reward: 34889.989, steps: 240
Episode 3: reward: 34889.989, steps: 240
Episode 4: reward: 34889.989, steps: 240
Episode 5: reward: 34889.989, steps: 240
Episode 6: reward: 34889.989, steps: 240
Episode 7: reward: 34889.989, steps: 240
Episode 8: reward: 34889.989, steps: 240
Episode 9: reward: 34889.989, steps: 240
Episode 10: reward: 34889.989, steps: 240

plot_x-p_pendulum

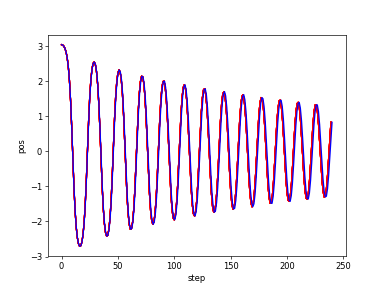
（２）カオスなDuffing振動子の深層強化学習

※コードは見出しからリンクしています

Training for 9600 steps ...
Interval 1 (0 steps performed)
 9600/10000 [===========================>..] - ETA: 5s - reward: 39.9779done, took 126.762 seconds
Testing for 5 episodes ...
Episode 1: reward: 11182.445, steps: 240
Episode 2: reward: 11182.445, steps: 240
Episode 3: reward: 11182.445, steps: 240
Episode 4: reward: 11182.445, steps: 240
Episode 5: reward: 11182.445, steps: 240
Testing for 10 episodes ...
Episode 1: reward: 11182.445, steps: 240
Episode 2: reward: 11182.445, steps: 240
Episode 3: reward: 11182.445, steps: 240
Episode 4: reward: 11182.445, steps: 240
Episode 5: reward: 11182.445, steps: 240
Episode 6: reward: 11182.445, steps: 240
Episode 7: reward: 11182.445, steps: 240
Episode 8: reward: 11182.445, steps: 240
Episode 9: reward: 11182.445, steps: 240
Episode 10: reward: 11182.445, steps: 240

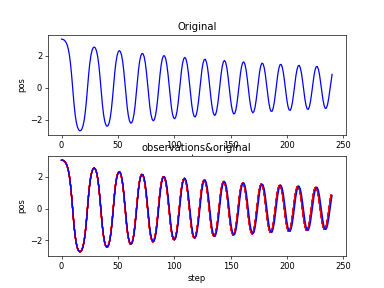
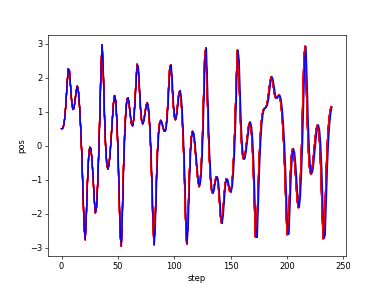
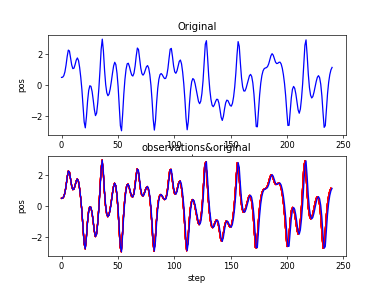
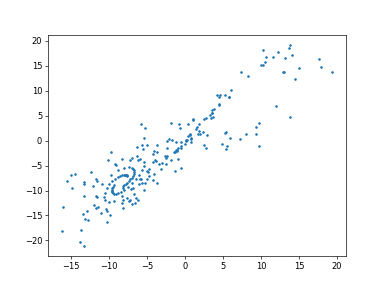
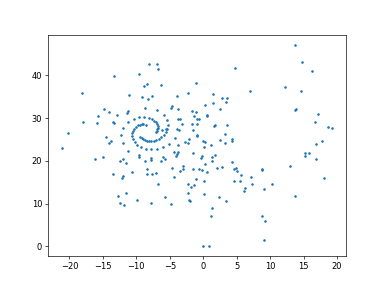
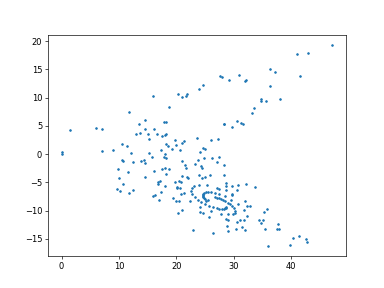
（３）カオスなLorenz方程式の解の深層強化学習

※コードは見出しからリンクしています

Training for 9600 steps ...
Interval 1 (0 steps performed)
 9600/10000 [===========================>..] - ETA: 5s - reward: -27.8420done, took 140.154 seconds
Testing for 5 episodes ...
Episode 1: reward: 0.000, steps: 240
Episode 2: reward: 0.000, steps: 240
Episode 3: reward: 0.000, steps: 240
Episode 4: reward: 0.000, steps: 240
Episode 5: reward: 0.000, steps: 240
Testing for 10 episodes ...
Episode 1: reward: 0.000, steps: 240
Episode 2: reward: 0.000, steps: 240
Episode 3: reward: 0.000, steps: 240
Episode 4: reward: 0.000, steps: 240
Episode 5: reward: 0.000, steps: 240
Episode 6: reward: 0.000, steps: 240
Episode 7: reward: 0.000, steps: 240
Episode 8: reward: 0.000, steps: 240
Episode 9: reward: 0.000, steps: 240
Episode 10: reward: 0.000, steps: 240

Lorenz_xt

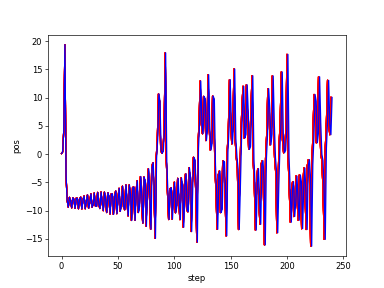
Lorenz_xt_obvs&original

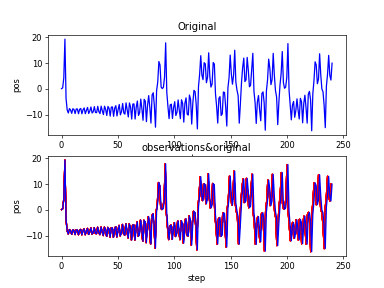
Lorenz_yt

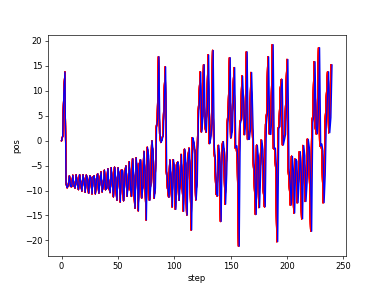
Lorenz_yt_obvs&original

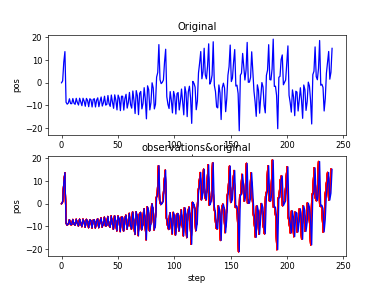
Lorenz_z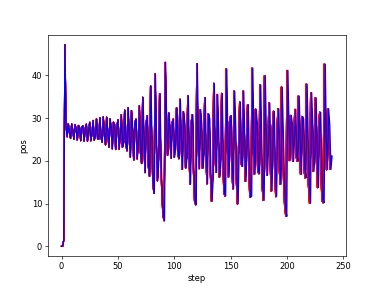t
t
Lorenz_zt_bvs&original

plot_xy

plot_yz

plot_zx

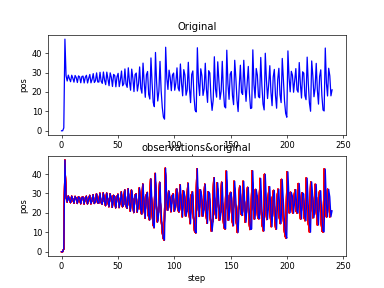
ちょっと考察

今回の特徴は無茶苦茶Testの結果がいいということである。
もちろん、Cartpoleは初期値こそ違うので一応運動学習をしたといえるけど、それでもその後の運動はほぼ一緒なのでそれもTest結果がよかった。

しかし、今回の自由な運動やカオスな運動のTestは初期値も同じだし、その後の動きも一緒なのでいわゆる学習データで検証しているようなものである。
ということでそれではそのパラメータを用いて未知の初期値を予測するとどうなるのかということに興味がわく。

ということで、パラメータをzvsｔのデータで学習し、その後 x vs. t やy vs. tに適用する
コードは以下を追加した。

# After training is done, we save the final weights.
dqn.save_weights('dqn_{}_weights.h5f'.format(ENV_NAME), overwrite=True)

zvs.tの学習

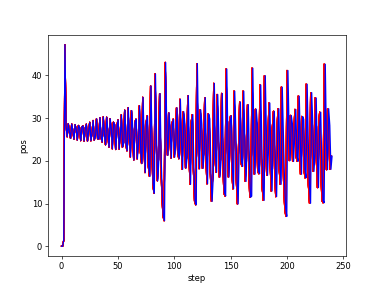
このときのパラメータを使って、xvs.tのデータで、しかも学習なしでdqn.testをやってみました。

dqn.load_weights('dqn_{}_weights.h5f'.format(ENV_NAME))
# トレーニングを開始。同じ正弦曲線を9600 = 240 x 400回 回す。
# histry = dqn.fit(env, nb_steps=9600, visualize=False, verbose=1)
# After training is done, we save the final weights.
# dqn.save_weights('dqn_{}_weights.h5f'.format(ENV_NAME), overwrite=True)
# トレーニング結果を確認
dqn.test(env, nb_episodes=5, visualize=False)

以下のように大きなrewardが得られました。

Testing for 5 episodes ...
Episode 1: reward: 317410.349, steps: 240
Episode 2: reward: 317410.349, steps: 240
Episode 3: reward: 317410.349, steps: 240
Episode 4: reward: 317410.349, steps: 240
Episode 5: reward: 317410.349, steps: 240
Testing for 10 episodes ...
Episode 1: reward: 317410.349, steps: 240
Episode 2: reward: 317410.349, steps: 240
Episode 3: reward: 317410.349, steps: 240
Episode 4: reward: 317410.349, steps: 240
Episode 5: reward: 317410.349, steps: 240
Episode 6: reward: 317410.349, steps: 240
Episode 7: reward: 317410.349, steps: 240
Episode 8: reward: 317410.349, steps: 240
Episode 9: reward: 317410.349, steps: 240
Episode 10: reward: 317410.349, steps: 240
Plotting Results

そして予測結果も以下のとおりほぼ完ぺきです。


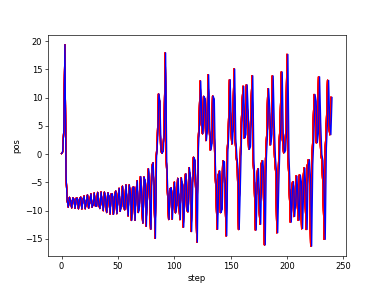
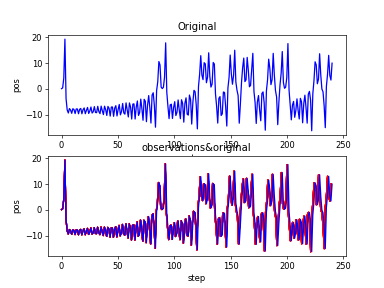
同じくyvs.tの学習を同じパラメータでやりました。今回は初期値を[0.1,0,0]から[0,10,20]へ
そして、区間も[0,48,240]から[48,96,240]へ変更して実施してみました。
その結果、以下のようにまたまた大きなrewardになりました。

Testing for 5 episodes ...
Episode 1: reward: 478383.841, steps: 240
Episode 2: reward: 478383.841, steps: 240
Episode 3: reward: 478383.841, steps: 240
Episode 4: reward: 478383.841, steps: 240
Episode 5: reward: 478383.841, steps: 240
Testing for 10 episodes ...
Episode 1: reward: 478383.841, steps: 240
Episode 2: reward: 478383.841, steps: 240
Episode 3: reward: 478383.841, steps: 240
Episode 4: reward: 478383.841, steps: 240
Episode 5: reward: 478383.841, steps: 240
Episode 6: reward: 478383.841, steps: 240
Episode 7: reward: 478383.841, steps: 240
Episode 8: reward: 478383.841, steps: 240
Episode 9: reward: 478383.841, steps: 240
Episode 10: reward: 478383.841, steps: 240

そして、以下のようにグラフもかなり良好な再現性となっています。

結果が良すぎてかなり引っ掛かりますが、検証のやり方が思い浮かばないので今回はここまでにしたいと思います。

まとめ

・カオスな運動の深層強化学習をやってみた
・フィッティングは通常の運動と同様綺麗に再現した。

・学習済パラメータを使って、同じLorenz方程式の未知データのフィッティングを実施したが、綺麗すぎる再現性を得た。
・今回示していないが、rewardが小さいのに再現する場合もあるのでどこか過誤がある

・本来model.predictから構成すべきだと考察されるので、初めに戻って再考察したいと思う
・dqnの学習とValidationについての知見がないのでさらに深堀して予言できるようにしたい