【感染症モデル入門】対数グラフを見てみると。。。「第二波だ」から1週間‼

前回の記事からもう一週間たったが、その後の傾向をまとめようと思う。
今回は、株価予想に使っているMACDを利用して、今後の状況を見たいと思う。
まず、現在の状況を普通の対数グラフで見ると、東京と全国はそれぞれ以下のとおりである。
東京は、既に第一波の最大値を超えて、なお指数関数的に増加中である。ただし、先週の日~水曜日が少し減少傾向を示したが、態勢には影響なしである。また、本日も206人と日曜日であるが、ほぼ同様な感染数となっている。

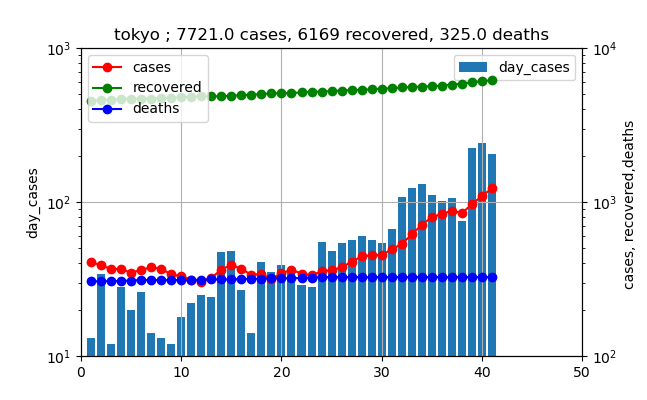
一方、全国も同様に指数関数的に増加している。全国も日~水曜日に減少が見られた。全国も本日371人とほぼ同様な感染数である。

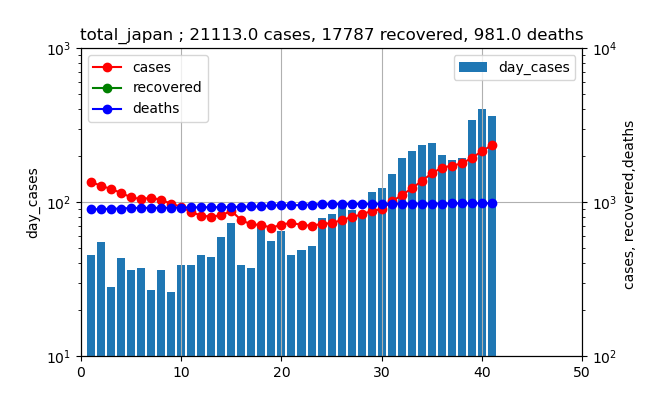
MACDを適用する

まず、第一波の3月下旬から4月末までの変化に適用する。
ロジックは簡単に記載すると以下のとおり

MACD＝12日EMA－26日EMA
Signal＝MACDの9日EMA
ヒストグラム＝Signal－MACD

ここで、EMA(Exponential Moving Average)は、以下の漸化式で計算される。

{S_{{t}}=\alpha \times Y_{{t-1}}+(1-\alpha )\times S_{{t-1}}
}

ここで、$Y_{{t-1}}$はt-1時点の観測値、$S_{{t-1}}$は一個前のEMAである。$\alpha = {2 \over {N+1}}$であり、N=9で0.2程度の値であり、$S_{{t}}$は今の観測点に近いほど大きく評価して平均に取り入れている。
ということで、第一波の時の動きは以下のとおりと計算できる。
東京は以下のとおり、減少傾向は4月17日以降ははっきり読み取れるが、ノイズが大きい。

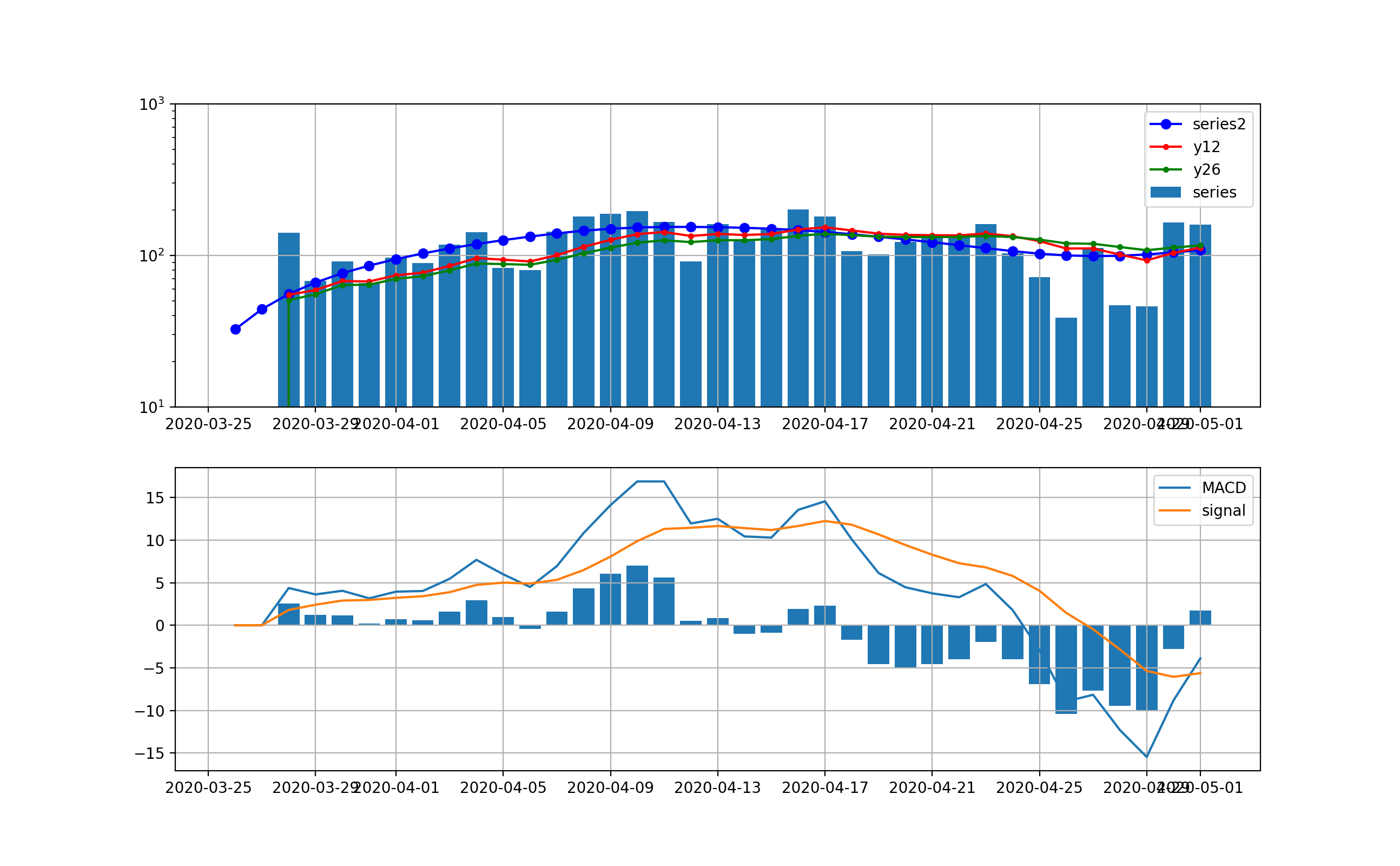
全国は以下のとおりで、ほぼ東京と同様に4月17日以降減少傾向が見て取れる。

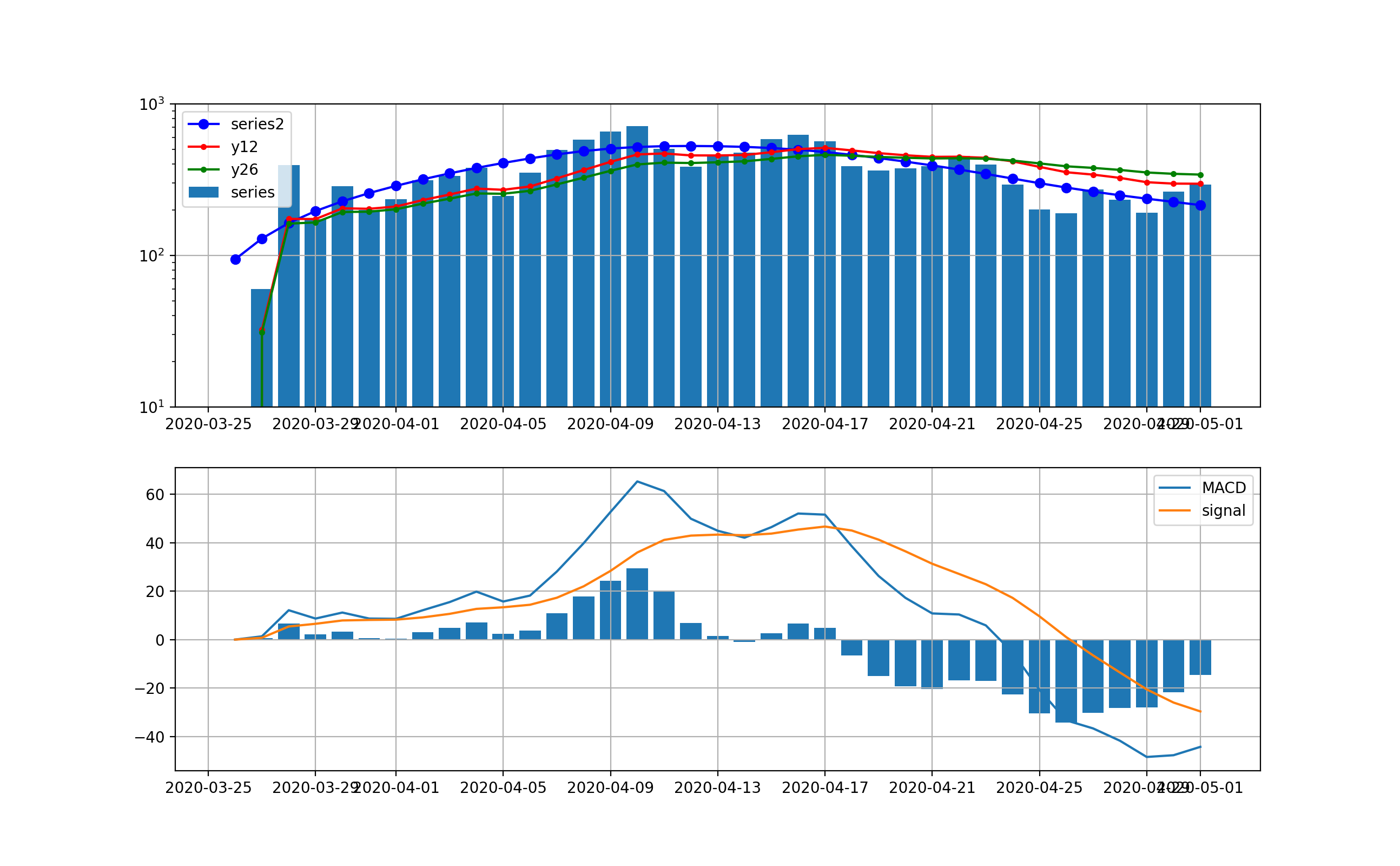
実は上記を見るとやはり毎日の変動が大きいので、シストレの記事と同様に、ここでDecomposeを導入してトレンド曲線を利用して同じ処理をしたものを示す。
東京は以下のとおりとなり、明らかに4月15日をピークとして減少傾向に転じていることが分かる。

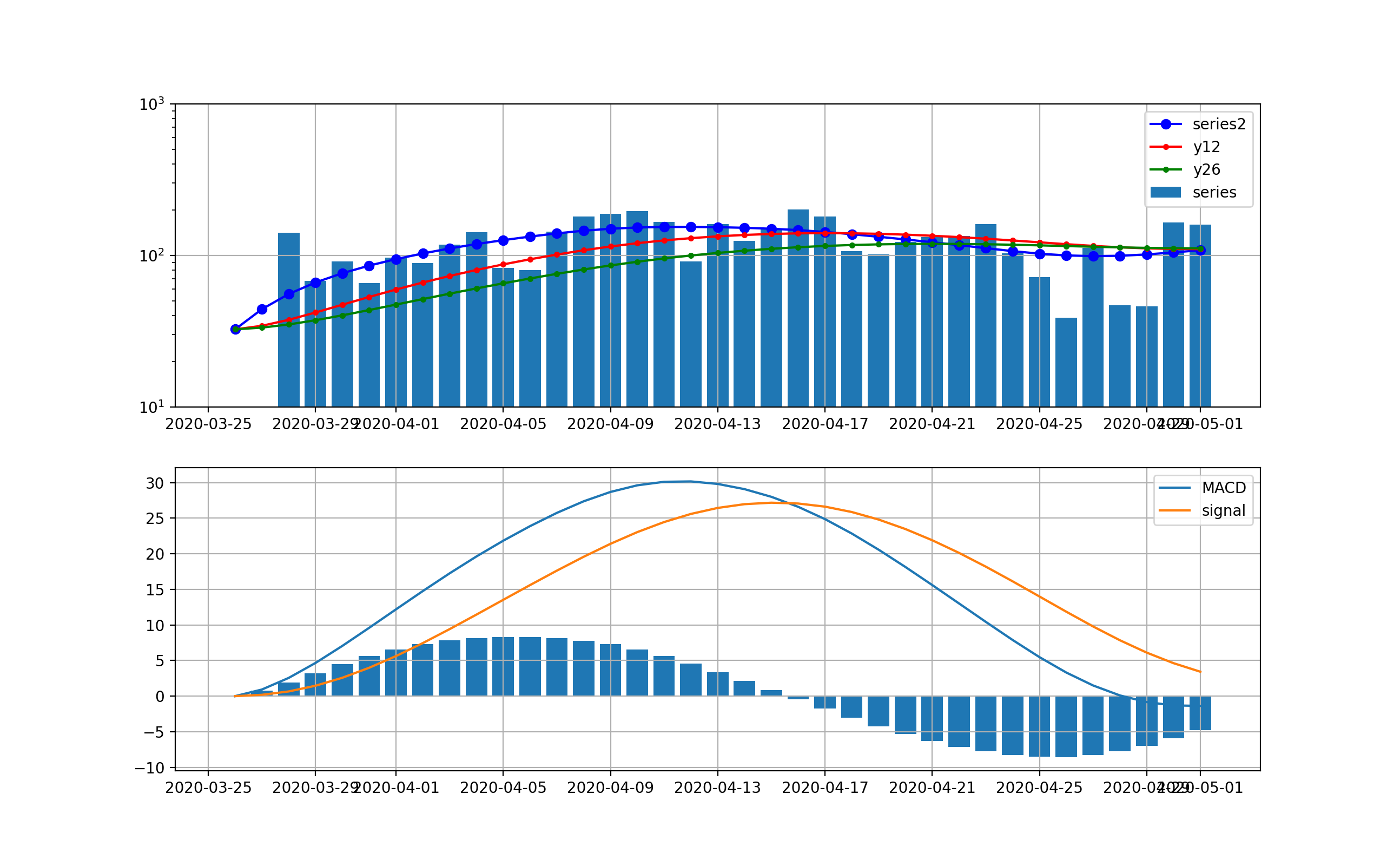
全国は以下のとおりとなった。こちらも4月16日をピークに減少傾向に転じている。

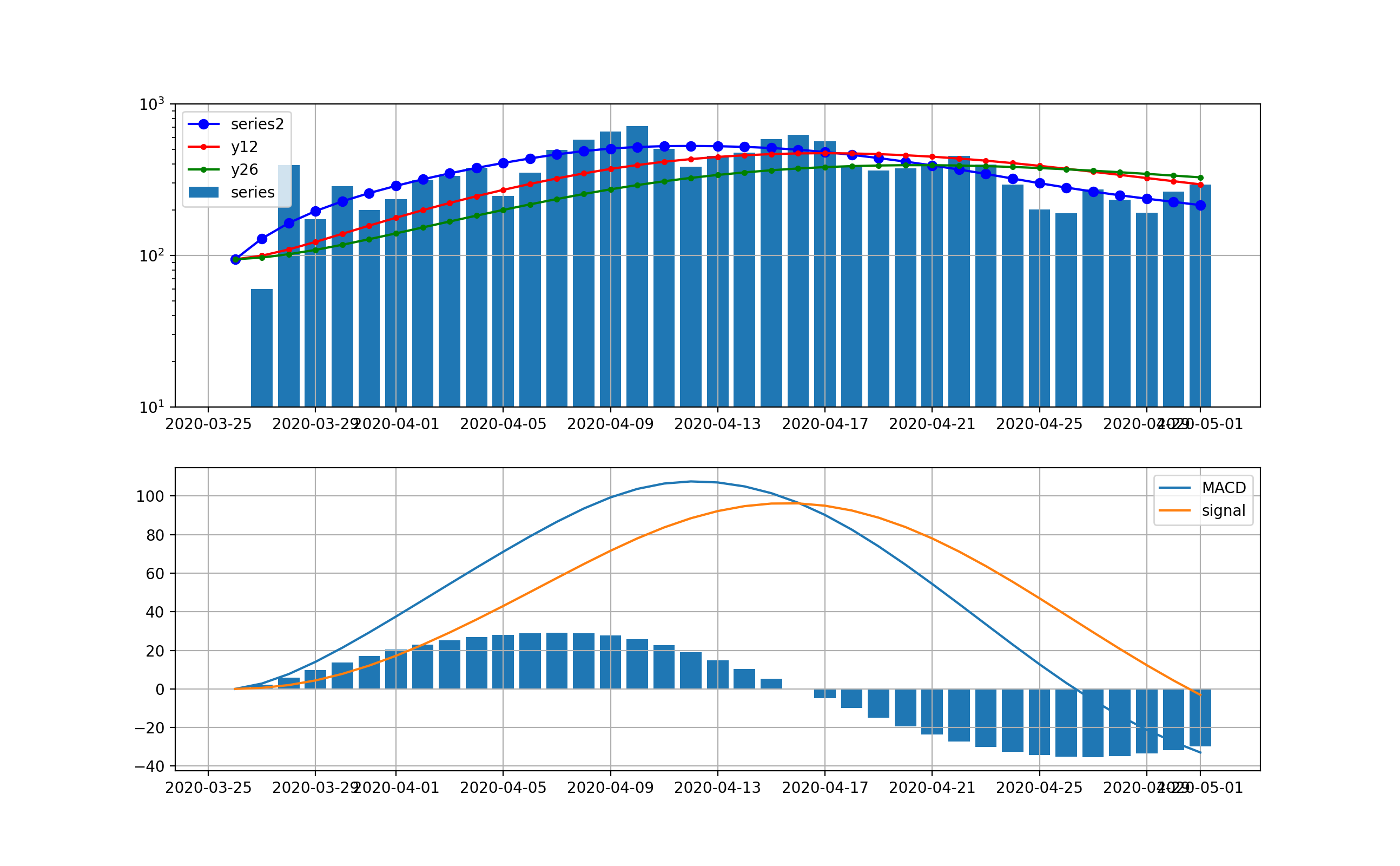
ということで、この解析方式はコロナの感染数の時系列でも感染数ピークを見るためには利用出来そうである。

第二波に適用する

東京の結果は以下のとおりとなった。
まず、処理なしに対する分析；この分析においても指数関数的な増加は明白であり、10日から２週間程度で500人レベルの感染数に到達しそうである。

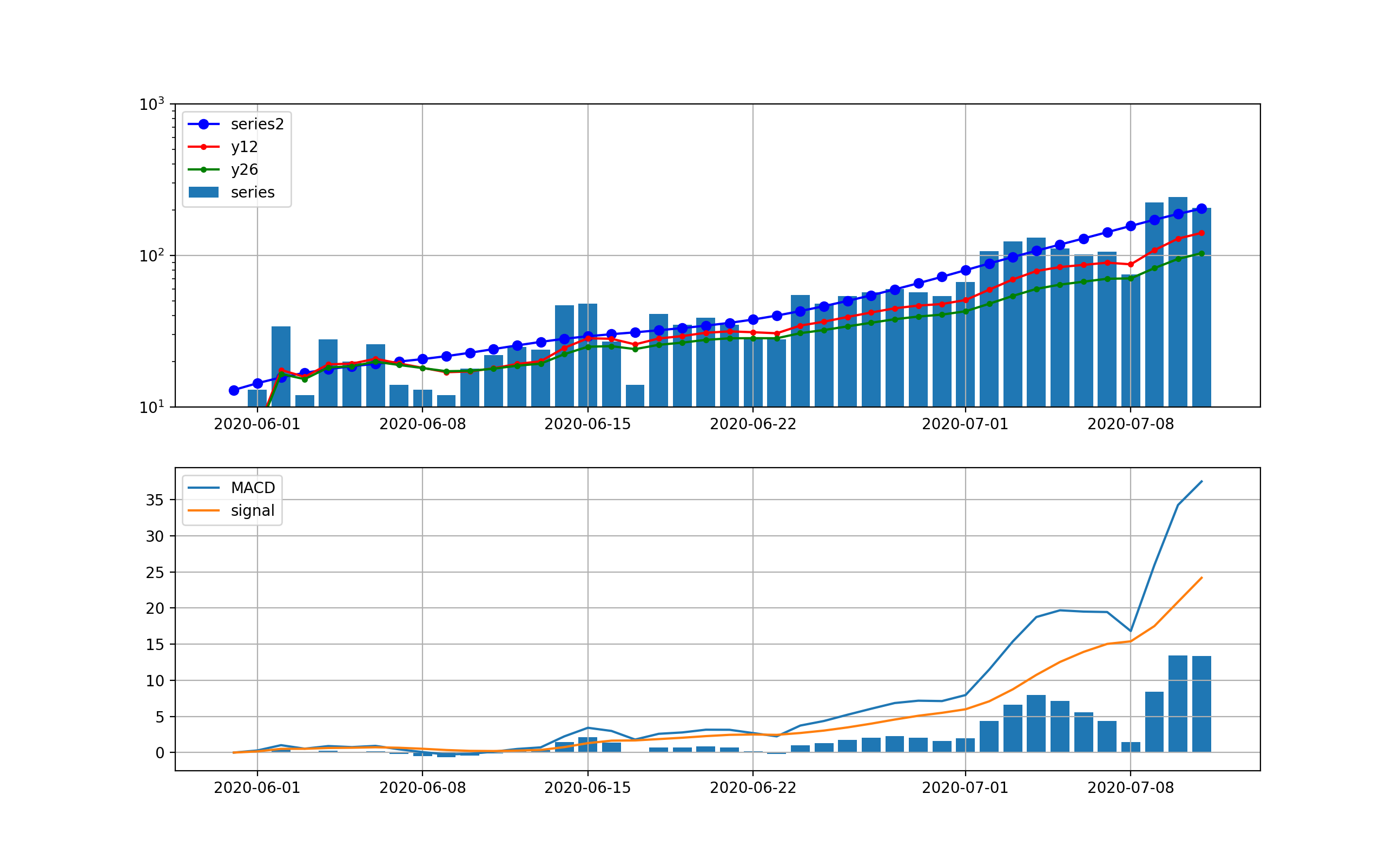
decomposeしてトレンド曲線に対する分析；こちらのグラフではさらに下がる気配は一向になく、当分この傾向が続くことが予想される。つまり、MACD曲線やsignal曲線は下に凸になっており、その差が当面増加することをうかがわせる。株価などはこの差が負へ転換するところが下落のシグナルとみなせるがこの図はその気配がない。

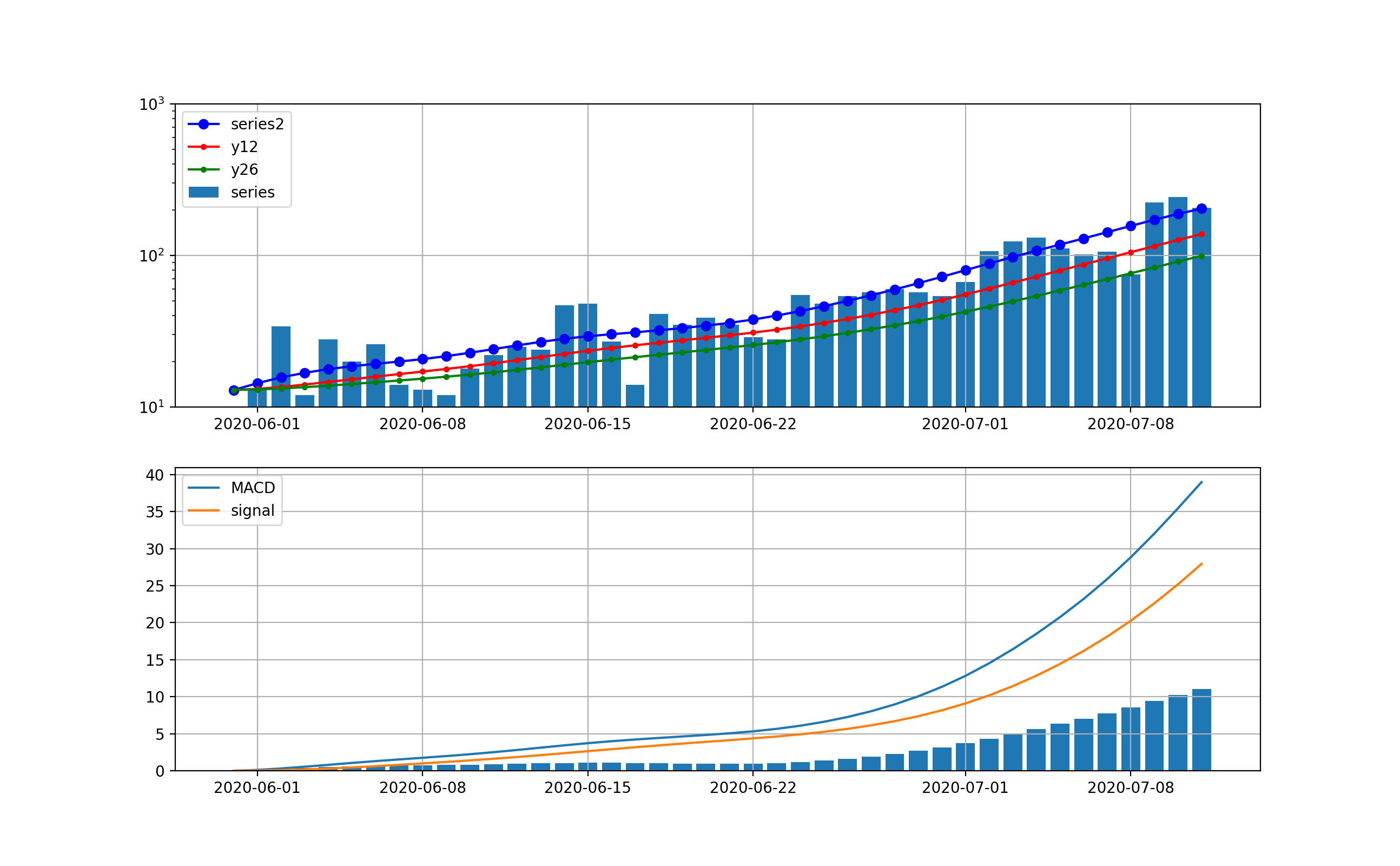
全国の分析も以下のとおり、ほぼ東京と同様な曲線である。

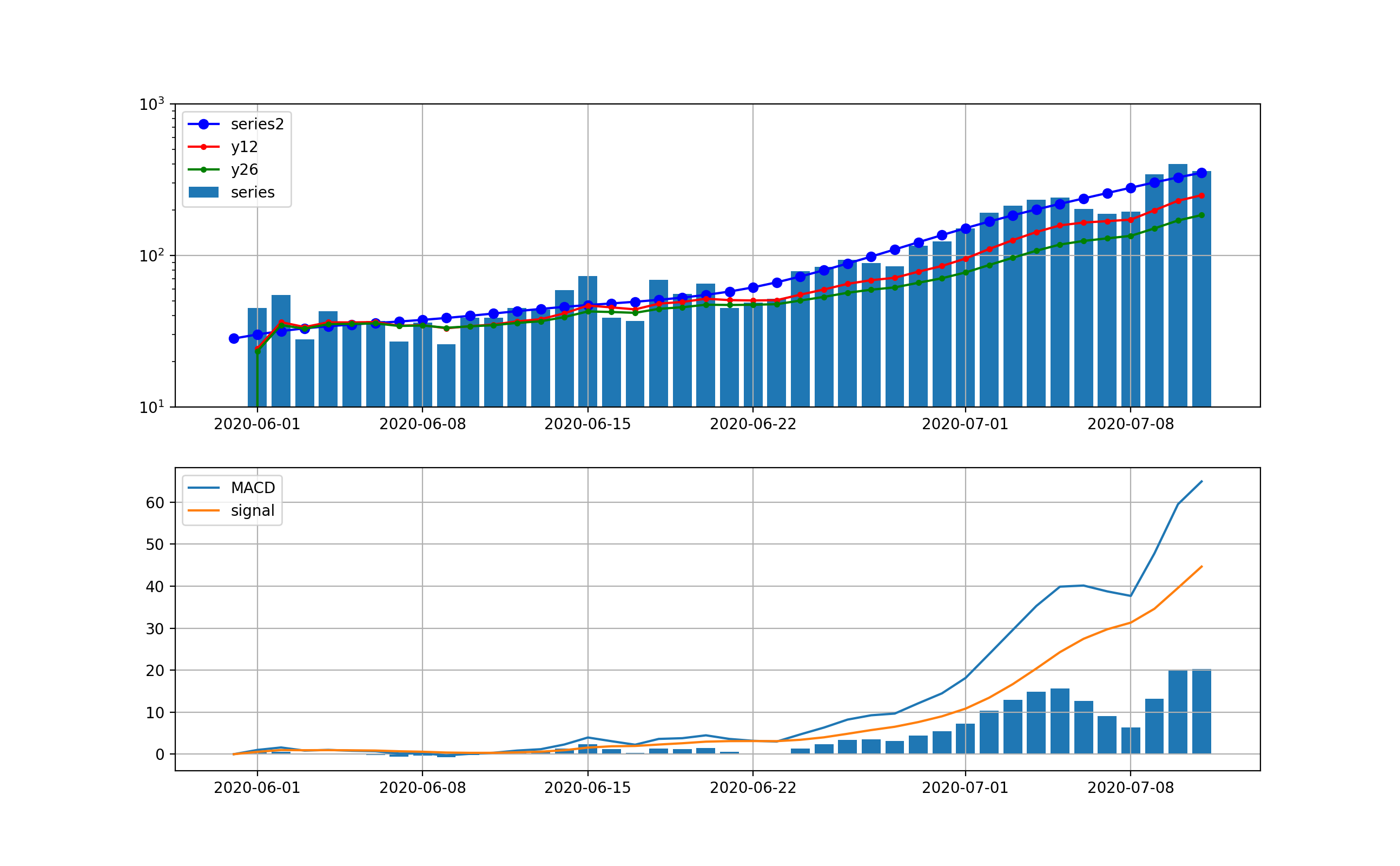
同じく、decomposeしてトレンド曲線に対する分析は以下のとおり

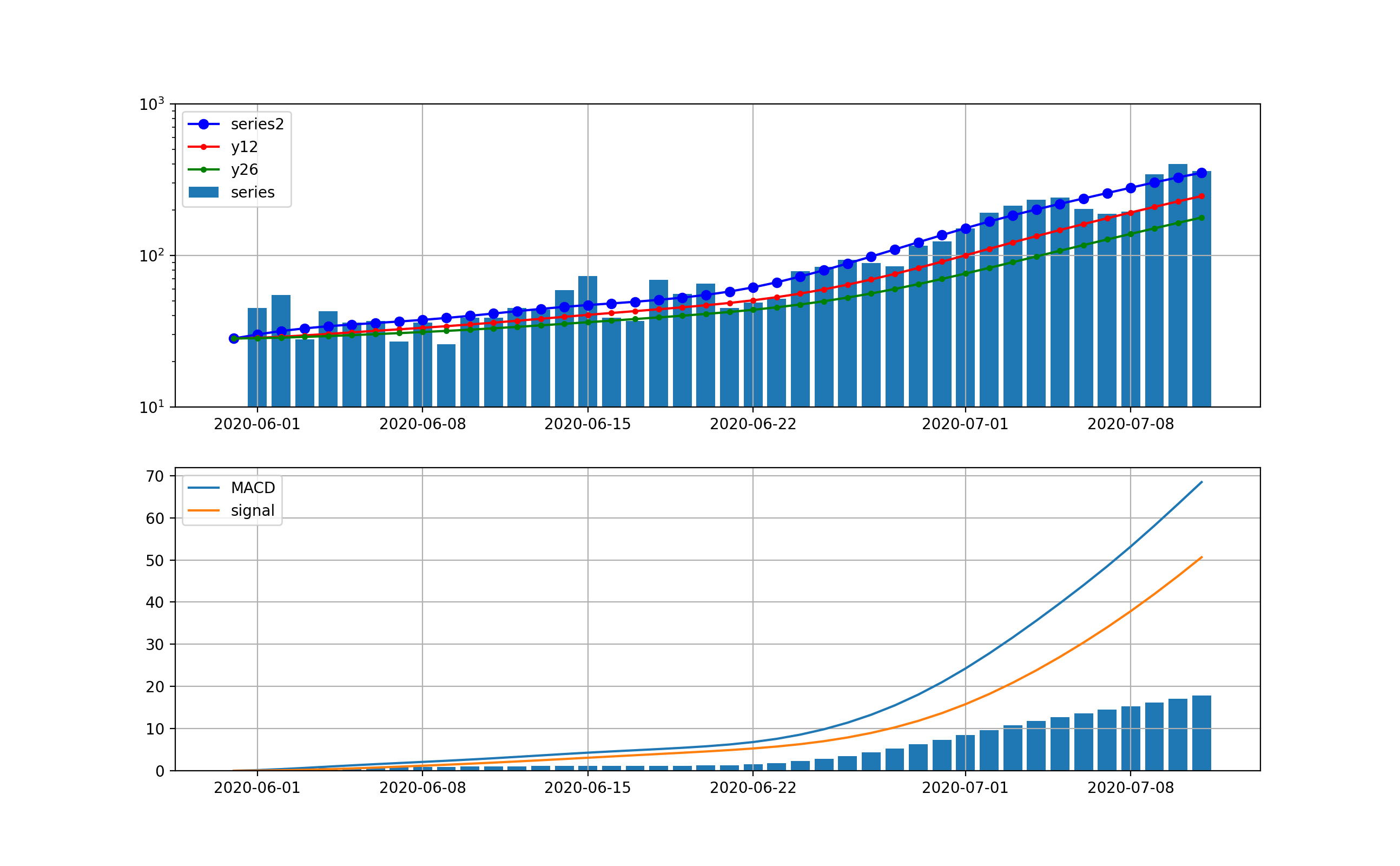
ちょっと背景分析

全国も東京と同様な傾向となっています。
もちろん首都圏の数字が大きいので同じような傾向になるのは当然な気がしますが、今回の第二波の開始は青いプロットの傾きやsignal-MACDの棒グラフの立ち上がりから、6月22日あたりである。
そこで、このトリガーが何に起因しているか、考えてみる。
トリガー候補は、以下の二つである。
①　緊急事態宣言解除が5月25日
②　東京アラート解除が6月11日
これらを比較して、感染から検査で発見されるまで10日程度と考えれていることから、どう見ても、東京アラート解除が増加のトリガーとなっていると考えるのが妥当なようだ。
逆に云うと、東京アラートは一定の効果があったとも言えそうである。

今後の感染数増加で危惧されること

まず、最初に見えてくるのは、最初のグラフで示した東京の感染数の赤いプロットを見ると、もはや1200程度まで増加しており、今後同じ指数で増加するように見える。
つまり、10日弱で3000床は埋まりそうな勢いである。
通常の入院日数は10日程度の報道があるので、10日弱で3000床というのはちょっと怖い数字である
そして次には重症患者の増加である。重症患者増加は時間遅れがあり、今は第一波の重傷者が回復しているので、減少に見える。しかし、これは第一波では7日から10日遅れ位で発生し始めており、これから発生することが危惧される。そして、今は若年層が7－8割と聞くのでその効果で重症化が抑えられている。しかし、感染数が多くなると高齢者の絶対数も増え、重症化の絶対数の増加は防げない。
そして最後に、医療がひっ迫し始める入院から40日後には死亡数も増え始める。

このままでは、東京ばかりか全国の感染拡大が止まる気配は無く、やはり限定的な非常事態宣言を発令して、東京からの移動制限や特定領域の業務制限などの処置をとって、できるだけ若者感染から高リスク者への感染を防ぐ措置をとる必要があると考える。
できるだけ、東京アラートと同様な強力な推進力を持って実施しないと拡大を抑えることはできないと想定される。

まとめ

・MACDを感染数予測に適用してみた
・指数関数的な継続的増加が示唆された
・とにかく初動（もう遅れ気味だが）が大切なので、東京アラート級の感染封じ込め措置を発令すべきである

・経済を回しながら、上記アラートをどのような対策セットとすべきかは重要なので早急に提言して実行してほしい

おまけ（とりあえずコード）

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
from pandas_datareader import data
import statsmodels.api as sm
from statsmodels.tsa.seasonal import STL

#pandasでCSVデータ読む。C:\Users\user\simulation\COVID-19\csse_covid_19_data\japan\test
data = pd.read_csv('data/covid19/test_confirmed.csv',encoding="cp932")
data_r = pd.read_csv('data/covid19/test_recovered.csv',encoding="cp932")
data_d = pd.read_csv('data/covid19/test_deaths.csv',encoding="cp932")
#data = pd.read_csv('data/test_confirmed_.csv',encoding="cp932")
#data_r = pd.read_csv('data/test_recovered_.csv',encoding="cp932")
#data_d = pd.read_csv('data/test_deaths_.csv',encoding="cp932")

confirmed = [0] * (len(data.columns) - 1)
day_confirmed = [0] * (len(data.columns) - 1)
confirmed_r = [0] * (len(data_r.columns) - 1)
day_confirmed_r = [0] * (len(data.columns) - 1)
confirmed_d = [0] * (len(data_d.columns) - 1)
diff_confirmed = [0] * (len(data.columns) - 1)
days_from_1_Jun_20 = np.arange(0, len(data.columns) - 1, 1)
beta_ = [0] * (len(data_r.columns) - 1)
gamma_ = [0] * (len(data_d.columns) - 1)
daystamp = "531"

#city,city0 = "東京","tokyo"
city,city0 = "合計","total_japan"

skd=1
#データを加工する
t_cases = 0
t_recover = 0
t_deaths = 0
for i in range(0, len(data_r), 1):
    if (data_r.iloc[i][0] == city): #for country/region
        print(str(data_r.iloc[i][0]))
        for day in range(1, len(data.columns), 1):            
            confirmed_r[day - 1] += data_r.iloc[i][day]
            if day < 1+skd:
                day_confirmed_r[day-1] += data_r.iloc[i][day]
            else:
                day_confirmed_r[day-1] += (data_r.iloc[i][day] - data_r.iloc[i][day-skd])/(skd)
        t_recover += data_r.iloc[i][day]        
for i in range(0, len(data_d), 1):
    if (data_d.iloc[i][0] == city): #for country/region
        print(str(data_d.iloc[i][0]) )
        for day in range(1, len(data.columns), 1):
            confirmed_d[day - 1] += float(data_d.iloc[i][day]) #fro drawings
        t_deaths += float(data_d.iloc[i][day])        
for i in range(0, len(data), 1):
    if (data.iloc[i][0] == city): #for country/region
        print(str(data.iloc[i][0]))
        for day in range(1, len(data.columns), 1):
            confirmed[day - 1] += data.iloc[i][day] -  confirmed_r[day - 1] -confirmed_d[day-1]
            if day == 1:
                day_confirmed[day-1] += data.iloc[i][day]
            else:
                day_confirmed[day-1] += data.iloc[i][day] - data.iloc[i][day-1]

def EMA1(x, n):
    a= 2/(n+1)
    return pd.Series(x).ewm(alpha=a).mean()                

day_confirmed[0]=0                
df = pd.DataFrame()                
date = pd.date_range("20200531", periods=len(day_confirmed))
df = pd.DataFrame(df,index = date)
df['Close'] = day_confirmed
df.to_csv('data/day_comfirmed_new_{}.csv'.format(city0))
date_df=df['Close'].index.tolist() #ここがポイント
print(date_df[0:30])
series = df['Close'].values.tolist()
stock0 = city0
stock = stock0
start = dt.date(2020,6,1)
end = dt.date(2020,7,12)

bunseki = "trend" #series" #cycle" #trend
cycle, trend = sm.tsa.filters.hpfilter(series, 144)
series2 = trend

y12 = EMA1(series2, 12)
y26 = EMA1(series2, 26)
MACD = y12 -y26
signal = EMA1(MACD, 9)
hist_=MACD-signal

ind3=date_df[:]
print(len(series),len(ind3))

fig, (ax1,ax2) = plt.subplots(2,1,figsize=(1.6180 * 8, 4*2),dpi=200)
ax1.bar(ind3,series,label="series")
ax1.plot(ind3,series2, "o-", color="blue",label="series2")
ax1.plot(ind3,y12, ".-", color="red",label="y12")
ax1.plot(ind3,y26, ".-", color="green",label="y26")
ax2.plot(ind3,MACD,label="MACD")
ax2.plot(ind3,signal,label="signal")
ax2.bar(ind3,hist_)
ax1.legend()
ax2.legend()
ax1.set_ylim(10,1000)
#ax2.set_ylim(10,1000)
ax1.set_yscale('log')
#ax2.set_yscale('log')
ax1.grid()
ax2.grid()
plt.savefig("./fig/{}/ema_decompose_%5K%25D_{}_{}new{}.png".format(stock0,stock,bunseki,start))
plt.pause(1)
plt.close()

df['Close']=series  #series" #cycle" #trend
df['series2']=series2
df['y12'] = EMA1(df['Close'], 12)
df['y26'] =  EMA1(df['Close'], 26)
df['MACD'] = df['y12'] -df['y26']
df['signal'] = EMA1(df['MACD'], 9)
df['hist_']=df['MACD']-df['signal']
date_df=df['Close'].index.tolist()
print(df[0:30])

fig, (ax1,ax2) = plt.subplots(2,1,figsize=(1.6180 * 8, 4*2),dpi=200)
ax1.bar(ind3,series, label="series")
ax1.plot(df['series2'],"o-", color="blue",label="series2")
ax1.plot(df['y12'],".-", color="red",label="y12")
ax1.plot(df['y26'],".-", color="green",label="y26")
ax2.plot(df['MACD'],label="MACD")
ax2.plot(df['signal'],label="signal")
ax2.bar(date_df,df['hist_'])
ax1.legend()
ax2.legend()
ax1.set_ylim(10,1000)
ax1.set_yscale('log')
ax1.grid()
ax2.grid()
plt.savefig("./fig/{}/ema_df_decompose_%5K%25D_{}_{}new{}.png".format(stock0,stock,bunseki,start))
plt.pause(1)
plt.close()