前回までで、【データサイエンティスト入門】記述統計と単回帰分析をまとめました。今回は確率と統計の基礎として確率/確率変数と確率分布をまとめます。本書に乗った解説を補足することとします。
【注意】
「東京大学のデータサイエンティスト育成講座」を読んで、ちょっと疑問を持ったところや有用だと感じた部分をまとめて行こうと思う。
したがって、あらすじはまんまになると思うが内容は本書とは関係ないと思って読んでいただきたい。
Chapter 4 確率と統計の基礎
Chapter 4-1 確率と統計を学ぶ準備
4-1-2 ライブラリのインポート
この章で使う、ライブラリのインポートをします。
※前回までと同様です
import numpy as np
import scipy as sp
import pandas as pd
from pandas import Series, DataFrame
import matplotlib as mpl
import seaborn as sns
import matplotlib.pyplot as plt
sns.set()
np.random.seed(0)
Chapter 4-2 確率
確率、試行、根元事象、標本空間、事象、条件付き確率、ベイズの定理、事前確率、事後確率
4-2-1 数学的確率
サイコロを題材として、確率を学ぶ上で必要な用語や概念を学習する。
# サイコロの取りうる値
dice_data =np.array([1,2,3,4,5,6])
4-2-1-1 事象
一つ一つの事象;根元事象
print('1つだけランダムに抽出', np.random.choice(dice_data,1))
# 1つだけランダムに抽出 [3]
全ての根元事象を集めた集合:標本空間Ω
標本空間の任意の部分集合:事象
ここで、1⇒10に変えると、以下も事象
print('10個ランダムに抽出', np.random.choice(dice_data,10))
# 10個ランダムに抽出 [2 3 4 2 2 1 6 2 2 5]
\begin{align}
& Kolmogorovの公理\\
&ある事象E(Event)が起こる確率P(E)と記せば、次を公理とする。\\
&公理1:すべての事象Aに対して0\leq P(A)\leq 1\\
&公理2;P(\Omega)=1\\
&公理3:互いに排反である加算個の事象、A_1,A_2,A_3,...に対して、\\
&P(A_1\cup A_2\cup A_3\cup...)=P(A_1)+P(A_2)+P(A_3)+...=\Sigma_i P(A_i)\\
\end{align}
本書の公理と異なりますが、参考書籍から引用します。
本書の公理3は、$A_1$,$A_2$の場合について記載しています。
【参考】
基礎系数学 確率・統計I p6 東京大学工学教程
4-2-1-2 空事象
空事象$\phi $は要素を全く持たない事象です。例えばA,Bが排反事象のとき$A\cap B$は空事象$\phi$です。$P(\phi)=0$です。
4-2-1-3 余事象
ある事象Eに属さない事象を余事象という。これはEの補集合とも言います。complementのcを使って表す。
E=\{2,4,6\}\\
E^c=\{1,3,5\}
4-2-1-4 積事象と和事象
A=\{1,2,3\}\\
B=\{1,3,4,5\}
$A\cap B$; 積事象
A\cap B = \{1,3\}
$A\cup B$; 和事象
A\cup B = \{1,2,3,4,5\}
4-2-1-5 確率の計算
「3が出る事象X」「空事象」「AとBの積事象」「AとBの和事象」がそれぞれ起こる確率を計算する。
\begin{align}
P(X) &= \frac{1}{6}\\
P(\phi ) &= 0\\
P(A\cap B)&=\frac{1}{3}\\
P(A\cup B)&=\frac{5}{6}\\
\end{align}
4-2-2 統計的確率
サイコロの目が出る確率
| 試行回数 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 10 | 0.1 | 0.5 | 0.2 | 0.1 | 0.1 | 0.0 |
| 100 | 0.16 | 0.17 | 0.18 | 0.19 | 0.18 | 0.12 |
| 1000 | 0.176 | 0.152 | 0.18 | 0.158 | 0.164 | 0.17 |
| 10000 | 0.1695 | 0.1701 | 0.1642 | 0.166 | 0.1617 | 0.1685 |
| 100000 | 0.16776 | 0.16621 | 0.16661 | 0.16573 | 0.16724 | 0.16645 |
| 1000000 | 0.166517 | 0.166637 | 0.166131 | 0.16692 | 0.166876 | 0.166919 |
| 以下は個人的見解ですが、... | ||||||
| この結果は、面白いと思います。 | ||||||
| つまり、6人の候補者がいて、有権者が均等(ランダム)に選んでいる場合でも、試行回数(有権者数)によっては結果に差がつくということで、有権者1000人位じゃちょっと優位性があるという場合だと、結果は信用できないのです。 | ||||||
| ということで、統計的に優位性を検証しないと真実は見えてこないし、一票を大切に投票しないということです。 |
calc_steps = 1000
print('calc_steps=',calc_steps)
dice_rolls = np.random.choice(dice_data,calc_steps)
for i in range(1,7):
p = len(dice_rolls[dice_rolls==i])/calc_steps
print(i, 'が出る確率;', p)
4-2-3 条件付き確率と乗法定理
事象Aが生じた条件のもとで事象Bが生じる確率を、Aが与えられたもとでのBの条件付き確率といい、
P(B|A)=\frac{P(A\cap B)}{P(A)}
と表します。この式は以下のように式変形して、これを乗法定理といいます。
P(A\cap B)=P(B|A)P(A)
具体例;
サイコロで、偶数の目
A={2,4,6}
4以上の事象
B={4,5,6}
AとBの積事象
$A\cap B = ${4,6}
P(B|A)=\frac{P(A\cap B)}{P(A)}=\frac{\frac{2}{6}}{\frac{3}{6}}=\frac{2}{3}
4-2-4 独立と従属
事象Aと事象Bが互いに独立であるとは、
P(A|B)=P(A)
が成り立つことである。
このとき、乗法定理から以下が成り立ちます。
P(A\cap B)=P(A)P(B)
この式が成立しない場合は、事象Aと事象Bとは互いに従属すると言います。上のサイコロの例で考えると以下の通りです。
\begin{align}
P(A\cap B)&=\frac{2}{6}&=\frac{1}{3}\\
P(A)P(B)&=\frac{3}{6}\frac{3}{6}&=\frac{1}{4}
\end{align}
となり等しくないため、事象Aと事象Bは独立ではなく、従属関係にあることが分かります。
C={1,3,5}の時はどうでしょう。
AとCの積事象
$A\cap C = ${}
この場合も、それぞれ0と$\frac{1}{4}$と等しくなく、従属関係です。
4-2-5 ベイズの定理
ベイズの定理を説明します。
参考から引用
「結果Aから原因Bを知りたい場合もある。...このような場合、Aを条件とするBの条件付き確率P(B|A)が必要となる。実験や調査などで求められるものはP(A|B)であるので、P(B|A)を計算する式が必要となる。」
上の条件付き確率のところで、Aを結果の事象、Bをその原因の事象と考えるとき、以下のベイズの定理が得られます。
これは、Aという結果が分かっているとき、その原因がB事象である確率を求めるものです。なお、$B^c$はBの補集合です。
P(B|A)=\frac{P(B\cap A)}{P(A)}\\
∵P(A\cap B)=P(B\cap A)\\
=\frac{P(A|B)P(B)}{P(A)}\\
=\frac{P(A|B)P(B)}{P(A|B)P(B)+P(A|B^c)P(B^c)}\\
P(B);事象Aが起こる前の事象Bの起こる確率;事前確率
P(B|A);事象Aが起きた後の事象Bの起こる確率;事後確率
P(A|B);Bが起きた場合にAが起こるであろう確率;尤度
以下を参考にしています。
【参考】
基礎系数学 確率・統計I p18 東京大学工学教程
「原因となる事象は$B_1,B_2,..., B_k$のk個あり、これらの事象は互いに排反事象で、これら以外の事象は起こらないとする。」と
P(A)=P[\cup _{i=1}^{k}(A\cap B_i)]\\
=\sum _{i=1}^{k}P(A\cap B_i)\\
=\sum _{i=1}^{k}P(A|B_i)P(B_i)
となる。
これを上式に代入すると、
P(B_i|A)=\frac{P(A|B_i)P(B_i)}{\sum _{j=1}^{k}P(A|B_j)P(B_j)}
練習問題4-1
| 試行回数 | 表 | 裏 |
|---|---|---|
| 10 | 0.6 | 0.4 |
| 100 | 0.51 | 0.49 |
| 1000 | 0.479 | 0.521 |
| 10000 | 0.505 | 0.495 |
| 100000 | 0.49939 | 0.50061 |
| 1000000 | 0.500783 | 0.499217 |
| 10000000 | 0.500065 | 0.499935 |
calc_steps = 1000
print('calc_steps=',calc_steps)
dice_rolls = np.random.choice(dice_data,calc_steps)
for i in range(0,2):
p = len(dice_rolls[dice_rolls==i])/calc_steps
print(i, 'が出る確率;', p)
Chapter 4-3 確率変数と確率分布
確率変数、確率関数、確率密度関数、期待値、一様分布、ベルヌーイ分布、二項分布、正規分布、ポアソン分布、対数正規分布、カーネル密度推定
4-3-1 確率変数、確率関数、分布関数、期待値
確率変数とは、とりうる値に対して確率が割り当てられる変数のことです。
サイコロで考えると、変数のとりうる値は1-6までの目であり、出現確率は以下の表のとおり、等しく1/6が割り当てられます。
ここで、変数Xを確率変数といい、とりうる値を示し、P(X)がそれぞれの出現確率です。
| X | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| P(X) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
| 大文字Xは確率変数、小文字xはその実現値をあらわす。 | ||||||
| また、大文字P(X)は出現確率、小文字p(x)はその実現値をあらわす。 |
\Sigma _{i=1}^6 p(x_i)= 1
4-3-1-1 分布関数
以下「」部分は、上の参考p21より引用。
「確率変数Xが離散型の場合、以下をXの確率分布とよぶ。
P(X=x_i) = f(x_i)
各点における確率は$x$(以下添え字iを省く)の関数であり、$f(x)$は確率関数と呼ぶ。」
分布関数(累積確率分布関数)は、以下で定義される。
F(X)=P(X\leq x) = \Sigma _{x_i \leq x}p(x_i)
ここで、連続確率変数である場合は、分布関数の導関数を密度関数(確率密度関数)といい、次のように定義する。
f(x)= \frac{dF(x)}{dx}
4-3-1-2 期待値(平均)
確率変数Xとすると、期待値E(X)の定義式は以下のようになる。
E(x)= \Sigma _x xf(x)
例えば、サイコロでは以下の通りとなる。
\begin{align}
E(x)&= 1*\frac{1}{6}+2*\frac{1}{6}+3*\frac{1}{6}+4*\frac{1}{6}+5*\frac{1}{6}+6*\frac{1}{6}\\
&=\frac{21}{6}\\
&=3.5
\end{align}
4-3-2 さまざまな分布関数
4-3-2-1 一様分布
全ての事象が起こる確率が等しいものは、一様分布と言われる。
サイコロの場合は、以下のとおり

prob_data = []
print('calc_steps=',calc_steps)
dice_rolls = np.random.choice(dice_data,calc_steps)
for i in range(1,7):
p = len(dice_rolls[dice_rolls==i])/calc_steps
prob_data.append(p)
print(i, 'が出る確率;', p)
plt.bar(dice_data, prob_data)
plt.grid()
plt.show()
>python dice_choice.py
calc_steps= 1000
1 が出る確率; 0.153
2 が出る確率; 0.17
3 が出る確率; 0.161
4 が出る確率; 0.17
5 が出る確率; 0.148
6 が出る確率; 0.198
4-3-2-2 ベルヌーイ分布
ベルヌーイ試行;結果が二値の試行
ベルヌーイ分布;一回のベルヌーイ試行において、各事象が生じる確率
コイン投げなら、表が出る確率、裏が出る確率
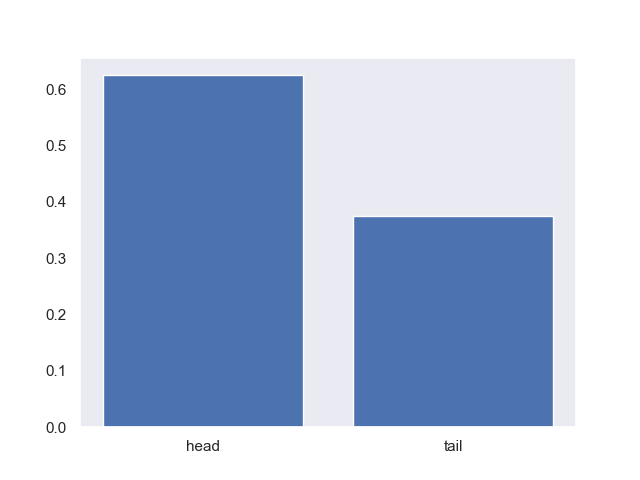
以下は、コインを8回投げた結果が[0,0,0,0,0,1,1,1]だった場合のベルヌーイ分布を求める。
prob_be_data = []
coin_data = np.array([0,0,0,0,0,1,1,1])
for i in np.unique(coin_data):
p = len(coin_data[coin_data==i])/len(coin_data)
prob_be_data.append(p)
print(i, 'が出る確率;', p)
plt.bar([0,1], prob_be_data, align = 'center')
plt.xticks([0,1], ['head', 'tail'])
plt.grid()
plt.show()
0 が出る確率; 0.625
1 が出る確率; 0.375
4-3-2-3 Pythonで分布に基づくデータを取得する
特定の分布に基づくデータを作る。以下numpyの各種分布関数を用いて計算して、分布データの特徴を見る。
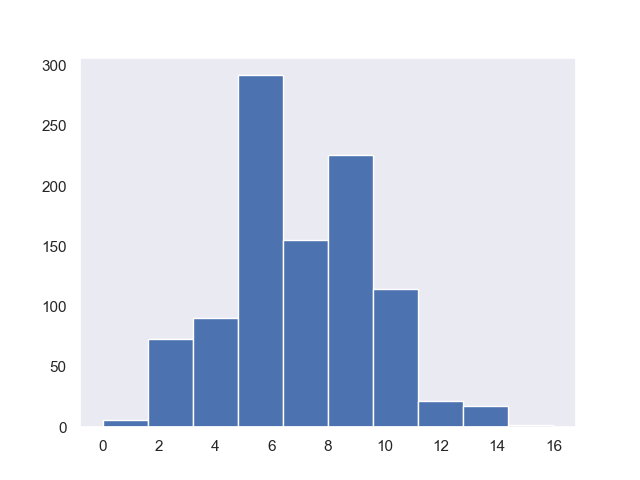
4-3-2-4 二項分布
二項分布は、独立なベルヌーイ試行をn回繰り返したもの。
以下のように生成できます。
(30回試行、確率0.5)で、1000回やってみた時は、以下の通り。
だいたい15辺りに平均があって、分散30/4
np.random.seed(0)
x = np.random.binomial(30,0.5,1000)
print(x.mean(), x.var())
# 14.98 7.6176
plt.hist(x)
plt.grid()
plt.show()
4-3-2-4 ポアソン分布
単位面積当たりの雨粒の数、1平米辺りの木の本数など。
ある区間で事象が発生すると見込まれる数を7とし、サンプル1000の時以下の通り。
np.random.seed(0)
x = np.random.poisson(7,1000)
print(x.mean(), x.var())
# 6.885 6.457775
plt.hist(x)
plt.grid()
plt.show()
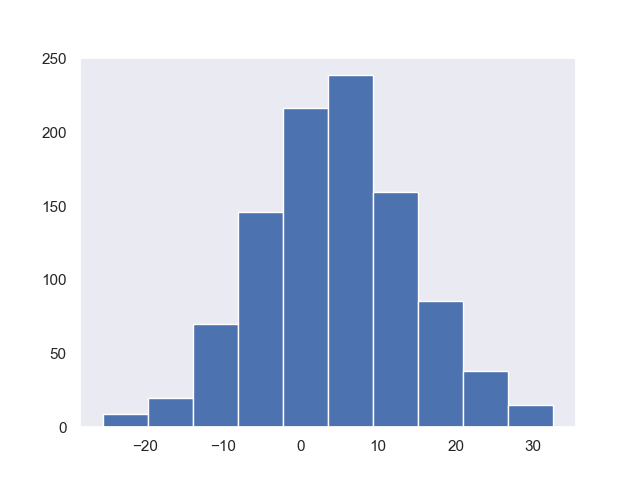
4-3-2-5 正規分布と対数正規分布
正規分布mu;平均値、sigma;標準偏差
np.random.seed(0)
x = np.random.normal(5,10,1000)
print(x.mean(), x.var())
# 4.547432925098047 97.42344563121543
plt.hist(x)
plt.grid()
plt.show()
np.random.seed(0)
mu, sigma = 3., 0.4
x = np.random.lognormal(mu,sigma,1000)
print(x.mean(), x.var())
# 21.329823289919993 76.9718785871209
plt.hist(x)
plt.grid()
plt.show()

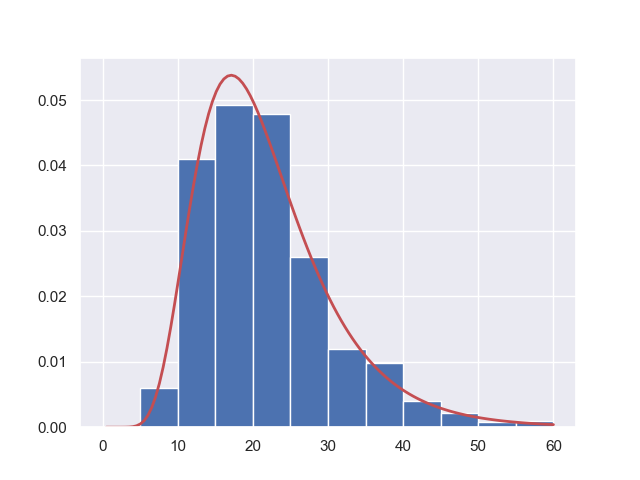
平均や標準偏差の意味が分かりにくいので、参考を見ながら、
縦軸を規格化し、式で計算したものと並べてみます。
※本書のパラメータは誤植と思われます
【参考】
numpy.random.lognormal
s = np.random.lognormal(mu, sigma, 1000)
count, bins, ignored = plt.hist(s, bins=12, range =(0,60), density=True, align='mid')
x = np.linspace(min(bins), max(bins),120)
pdf = (np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))/ (x * sigma * np.sqrt(2 * np.pi)))
plt.plot(x, pdf, linewidth=2, color='r')
plt.axis('tight')
plt.show()
4-3-3 カーネル密度関数
与えられたデータを使って密度関数を推定する。
カーネル密度関数を使って、欠席数のデータを推定するには、以下の通り実施します。
student_data_math = pd.read_csv('./chap3/student-mat.csv', sep =';')
student_data_math.absences.plot(kind='kde', style='k--')
student_data_math.absences.hist(density=True,align='mid')
plt.grid()
plt.show()
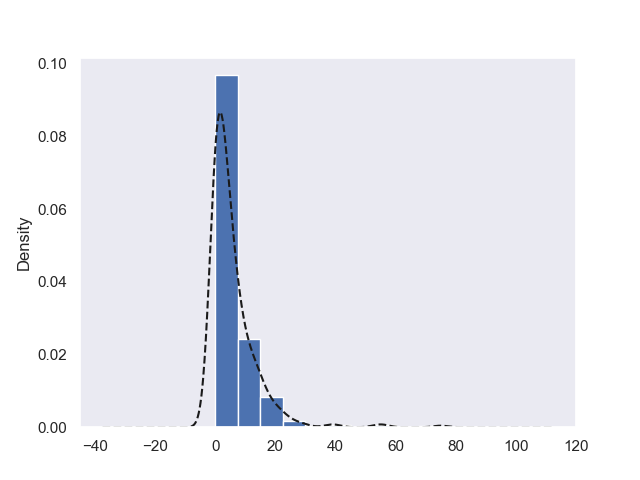
kdeってどんな関数を仮定しているのか、もう一つ理解できないので、参考より
【参考】
カーネル密度推定@wikipedia
「x1, x2, ..., xn を(未知の)確率密度関数 ƒ を持つ独立同分布からの標本とする。カーネル関数 K、バンド幅(平滑化パラメータ)h のカーネル密度推定量(英: kernel density estimator)とは
\begin{align}
f(x)&=\frac{1}{nh}∑^n_{i=1}K(\frac{x−X_i}{h})\\
\\
ここで通常カーネル&関数は以下の正規分布が利用される。\\
\\
K(x)&=\frac{1}{2\pi}e^{\frac{x^2}{2}}\\
\end{align}
Chapter 4-4 多次元確率分布
同時確率分布、周辺確率関数、条件付き確率関数、条件付き平均、分散共分散行列、多次元正規分布
4-4-1 同時確率関数と周辺確率関数
Xが${x_0,x_1,...}$、Yが${y_0,y_1,...}$上で値を取る離散型の確率変数を考える。$X=x_i$と$Y=y_i$である確率を以下のように書くとすると、以下を同時確率関数という。
P(X=x_i, Y=y_i) = p_{X,Y}\{x_i,y_i\}
また、以下をXの周辺確率関数という。
P_X(x_i) = \Sigma _{j=0}^{\infty }p_{X,Y}\{x_i,y_i\}
Yについても同様に定義される。
4-4-2 条件付き確率関数と条件付き期待値
$X=x_i$を与えた時の$Y=y_i$の条件付き確率関数は以下のように定義できる。
p_{Y|X}(y_j|x_i)=P(Y=y_j|X=x_i)=\frac{p_{X,Y}(x_i,y_j)}{p_X(x_i)}
また、$X=x_i$を与えた時のYの条件付き期待値は以下のようになります。
E[Y|X=x_i]=\Sigma _{j=1}^{\infty }y_jp_{Y|X}(y_j|x_i)=\frac{\Sigma _{j=1}^{\infty }y_ip_{X,Y}(x_i,y_j)}{p_X(x_i)}
4-4-3 独立の定義と連続分布
2変数における独立の定義は、すべてのxi, yi に関して、以下が成り立つときに独立であるとする。
p_{X|Y}(x_i|y_j)=p_X(x_i)p_Y(y_j)
なお、連続分布についても、同時確率密度関数、周辺確率密度関数、条件付き確率密度関数、独立の定義など定義できますが、割愛します。
4-4-3-1 2次元の正規分布をグラフで表示する
以下のプログラムで以下のようなグラフが表示されました。
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as st
from scipy.stats import multivariate_normal
from mpl_toolkits.mplot3d import Axes3D
x,y =np.mgrid[10:100:2,10:100:2]
pos = np.empty(x.shape + (2,))
pos[:,:,0]=x
pos[:,:,1]=y
rv = multivariate_normal([50,50],[[100,0],[0,100]])
z=rv.pdf(pos)
fig = plt.figure(dpi=100)
ax=Axes3D(fig)
ax.plot_wireframe(x,y,z)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x,y)')
ax.ticklabel_format(style='sci', axis = 'z',scilimits=(0,0))
plt.show()
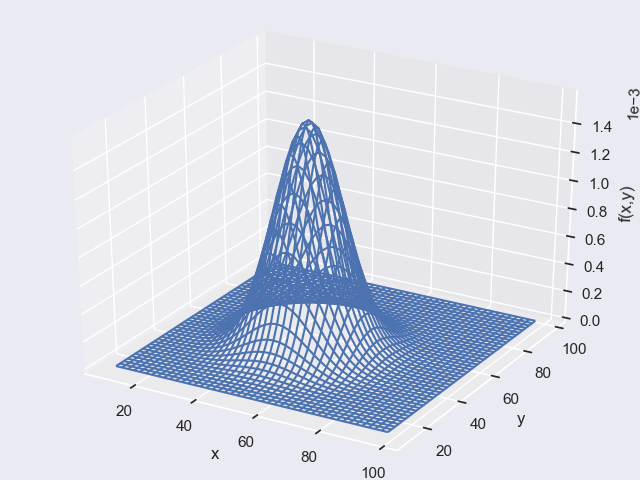
ちょっと、プログラムも難しいので解説します。
以下の二行を理解することが大切です。
rv = multivariate_normal([50,50],[[100,0],[0,100]])
z=rv.pdf(pos)
以下の参考が理解の役に立ちます。
【参考】
①多変量正規分布@wikipedia
②多次元正規分布に従うデータを生成する
参考②によれば、上のコードは以下のように書けます。
ここで、muは平均、sigmaは共分散行列です。
mu = [50,50]
sigma = [[100,0],[0,100]]
rv = multivariate_normal(mu, sigma)
式で書くと以下のとおりです。
\mu=\begin{pmatrix}\mu_x \\ \mu_y \end{pmatrix}\\
\sum=
\begin{pmatrix} \sigma_x^2 & Cov(x,y) \\ Cov(y,x) & \sigma_y^2 \end{pmatrix}\\
=\begin{pmatrix} \sigma_x^2 & \rho \sigma_x\sigma_y \\ \rho\sigma_y\sigma_x & \sigma_y^2 \end{pmatrix}
すなわち、ここでは以下の通りおいています。
\mu=\begin{pmatrix} 50 \\ 50\end{pmatrix}\\
\sum=\begin{pmatrix}100 & 0 \\ 0 & 100\end{pmatrix}
そして、multivariate_normal(mu, sigma)全体の式は以下の計算を(x,y)の組について、z=rv.pdf(pos)でグリッドで計算していることになります。
f(x,y)=\frac{1}{2\pi\sigma_x\sigma_y\sqrt{1-\rho^2}}\exp(-\frac{1}{2(1-\rho^2)}[\frac{(x-\mu_x)^2}{\sigma_x^2}+\frac{(y-\mu_y)^2}{\sigma_y^2}-\frac{2\rho(x-\mu_x)(y-\mu_y)}{\sigma_x\sigma_y}])
また、ほぼ同じようなコードが以下の参考③で掲出されています。
【参考】
③Python plot 3d scatter and density
④scipy.stats.multivariate_normal
また、z=rv.pdf(pos)を理解するためには、pdfは以下の意味であり、おまけに書いたような引数を取ります。今は以下を使っています。
pdf=Probability density function.
関数定義して独自計算
【参考】
Python 3:3次元グラフの書き方(matplotlib, pyplot, mplot3d, MPL)
コードは以下の通りになります。
※利用するライブラリは上と同様です
def func(x,y):
mux,muy,sigmax,sigmay,rho=50.,50.,10.,10.,0.
fxy=np.exp(-((x-mux)**2/(sigmax**2) + (y-muy)**2/(sigmay**2)-2*rho*(x-mux)*(y-muy)/(sigmax*sigmay))/2*(1-rho**2))/(2*np.pi*sigmax*sigmay*np.sqrt(1-rho**2))
return fxy
x,y =np.mgrid[10:100:2,10:100:2]
z=func(x,y)
fig = plt.figure(dpi=100)
ax=Axes3D(fig)
ax.plot_wireframe(x,y,z)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x,y)')
ax.ticklabel_format(style='sci', axis = 'z',scilimits=(0,0))
plt.show()
体裁一緒なので以下のように同じ絵が得られました。
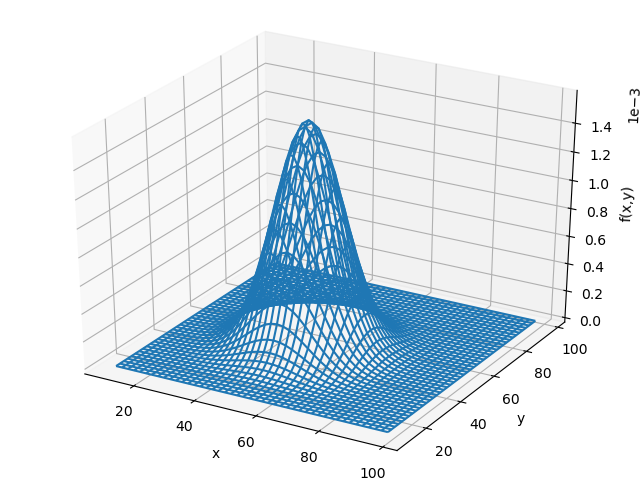
mux,muy,sigmax,sigmay,rho=50.,50.,10.,10.,0.3のとき
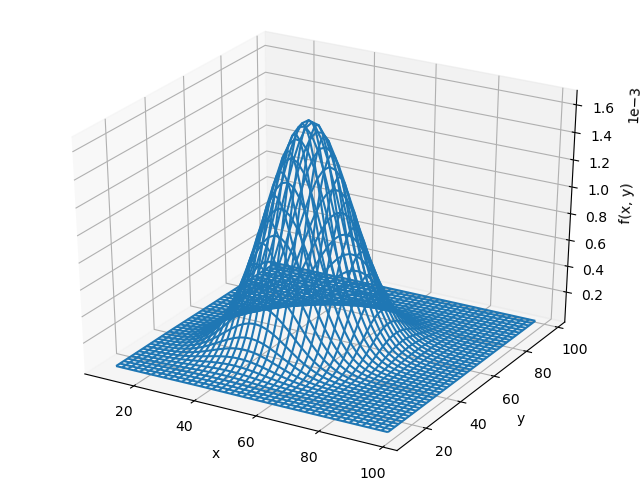
そして、
rv = multivariate_normal([50,50],[[100,30],[30,100]])
で計算してみると、以下のように同じ結果となりました。

おまけ
rv = multivariate_normal(mu, sigma)のrv.Methods()として求められるもの
| Methods | 解説 |
|---|---|
pdf(x, mean=None, cov=1, allow_singular=False) |
Probability density function. |
logpdf(x, mean=None, cov=1, allow_singular=False) |
Log of the probability density function. |
cdf(x, mean=None, cov=1, allow_singular=False, maxpts=1000000*dim, abseps=1e-5, releps=1e-5) |
Cumulative distribution function. |
logcdf(x, mean=None, cov=1, allow_singular=False, maxpts=1000000*dim, abseps=1e-5, releps=1e-5) |
Log of the cumulative distribution function. |
rvs(mean=None, cov=1, size=1, random_state=None) |
Draw random samples from a multivariate normal distribution. |
entropy() |
Compute the differential entropy of the multivariate normal. |