今夜は、「③音声や地震データや株価や、。。。とにかく一次元の実時系列データに応用する」をやってみました。実データは調整ができないので、事前のデータ処理も限界があって、やってみるとハマることハマること。。。
とりあえずの目標
以下のとおり、
※リンクされているものは記事にしたものであり、その記事を前提知識として書いて行くので、参照すると理解し易いと思います。
①Scipy環境を作る
・環境の確認
②不確定原理について
・FFT変換・逆変換してみる;時間軸が消える
・STFT変換・逆変換してみる;窓関数について
・wavelet変換・逆変換してみる;スペクトログラムの解釈と不確定原理
③音声や地震データや株価や、。。。とにかく一次元の実時系列データに応用する
④FFTからwavelet変換まで簡単にたどってみる(上記以外のちょっと理論)
⑤二次元データに応用してみる
⑥天体観測データに応用してみる
⑦リアルタイムにスペクトログラムしてみる
今回やったこと
「③音声や地震データや株価や、。。。とにかく一次元の実時系列データに応用する」の最もポピュラーな音声データについて、以下の三通りを実行して比較してみます。
音声データについては、以前RasPiで取得したものがあり、そのデータを利用します。
※wavファイル取得については、別途記事にしたいと思います。なお、今回は以下の参考のコードを参考にしています
【参考】
・Pythonで読み込んだwavファイルをFourier変換して逆変換して再度書き出す
※今回は以下を並べることによりその特徴が見えてくることを期待します
・FFT変換・逆変換してみる;単に全領域でFFTしてみました
・STFT変換・逆変換してみる;適当な窓関数について実行してみました
・wavelet変換・逆変換してみる;こちらも適当な窓関数について実行してみました
・FFT変換・逆変換してみる;単に全領域でFFTしてみました
from scipy.fftpack import fft, ifft
import numpy as np
import matplotlib.pyplot as plt
import wave
import struct
from pylab import *
from scipy import signal
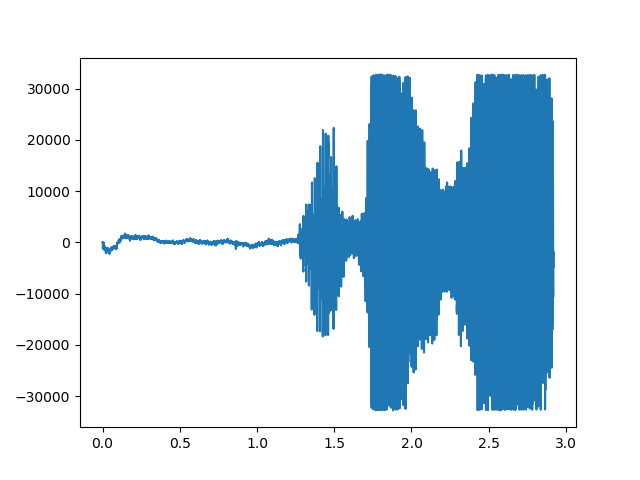
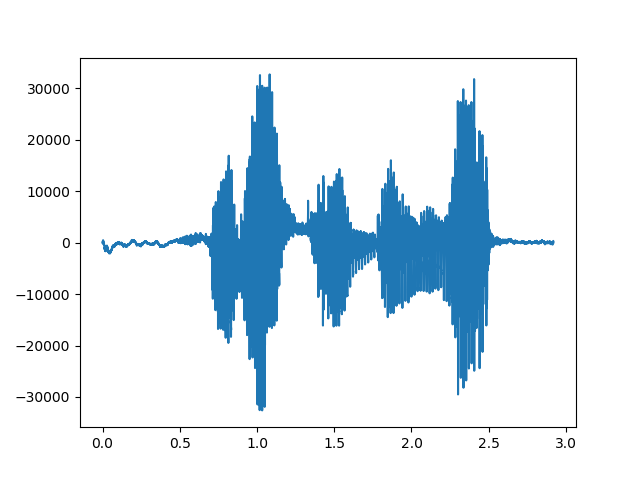
今回の音声ファイルは、「開けゴマ」「おはよう」としました。
※どちらも録音は汚いモノラルですが、。。
# wavfile = 'hirakegoma.wav'
wavfile = 'ohayo.wav'
wr = wave.open(wavfile, "rb")
したがって、ch=1
ch = wr.getnchannels()
幅は、出力見ると2だそうです。
width = wr.getsampwidth()
フレーム周波数がサンプリング周波数で、今回は22.1kHzです。
フレーム数は、64512
この二つの数字から、総サンプリング時間fsが得られます。
fr = wr.getframerate()
fn = wr.getnframes()
fs = fn / fr
print('ch', ch)
print('frame', fn)
print('fr',fr)
print('sampling fs ', fs, 'sec')
print('width', width)
origin = wr.readframes(wr.getnframes())
data = origin[:fn]
wr.close()
amp = max(data)
print(amp)
print('len of origin', len(origin))
print('len of sampling: ', len(data))
参考先のページでは、ステレオサウンド取得のようですが、今回はモノラルです。
# ステレオ前提 > monoral
sig = np.frombuffer(data, dtype="int16") #/32768.0
t = np.linspace(0,fs, fn/2, endpoint=False)
plt.plot(t, sig)
plt.show()
freq =fft(sig,int(fn/2))
Pyy = np.sqrt(freq*freq.conj())*2/fn
f = np.arange(int(fn/2))
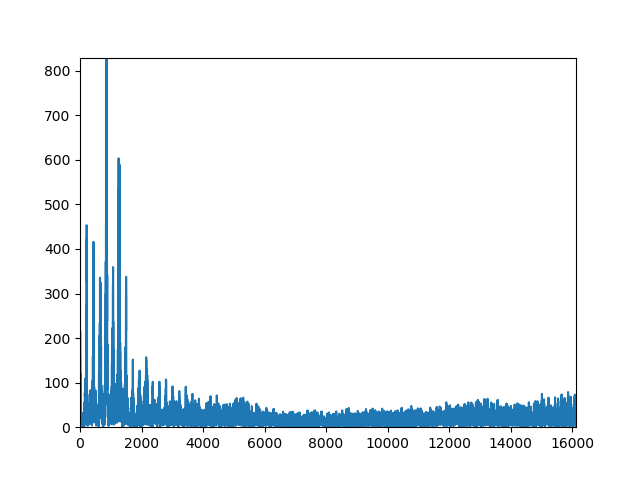
plt.plot(f,Pyy)
plt.axis([0, max(f)/2, 0,max(Pyy)])
plt.show()
おはよう
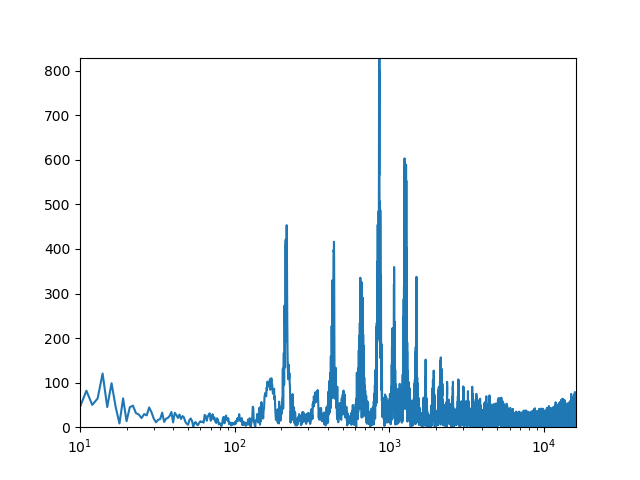
plt.axis([10, max(f)/2, 0,max(Pyy)])に変更して対数表示plt.xscale('log')します。
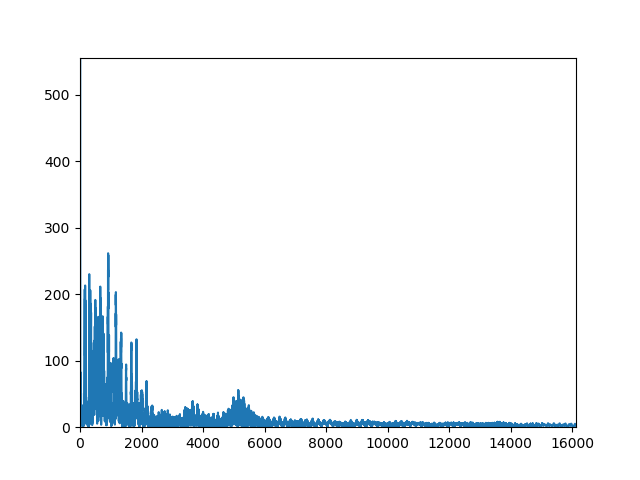
開けゴマ
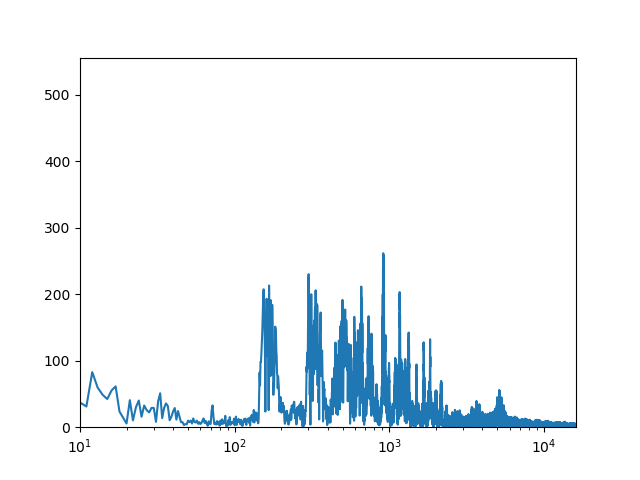
plt.axis([10, max(f)/2, 0,max(Pyy)])に変更して対数表示plt.xscale('log')します。
逆変換は、特に処理せずまんま戻しています。
t1 = np.linspace(0,fs, fn/2, endpoint=False)
sig1=ifft(freq,fn/2)
plt.plot(t1, sig1)
plt.axis([0, fs, min(sig1), max(sig1)])
plt.show()
・STFT変換・逆変換してみる;適当な窓関数について実行してみました
import wave
from scipy import fromstring, int16
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
# wavfile = 'hirakegoma.wav'
wavfile = 'ohayo.wav'
wr = wave.open(wavfile, "rb")
ch = wr.getnchannels()
width = wr.getsampwidth()
fr = wr.getframerate()
fn = wr.getnframes()
nperseg = 256 #4096 #2048 #1024 #256 #128 #32 #64 #512
print('ch', ch)
print('frame', fn)
fs = fn / fr
print('fr',fr)
print('sampling fs ', fs, 'sec')
print('width', width)
origin = wr.readframes(wr.getnframes())
data = origin[:fn]
wr.close()
amp = max(data)
print('amp',amp)
print('len of origin', len(origin))
print('len of sampling: ', len(data))
# ステレオ前提 > monoral
x = np.frombuffer(data, dtype="int16") #/32768.0
print('max(x)',max(x))
t = np.linspace(0,fs, fn/2, endpoint=False)
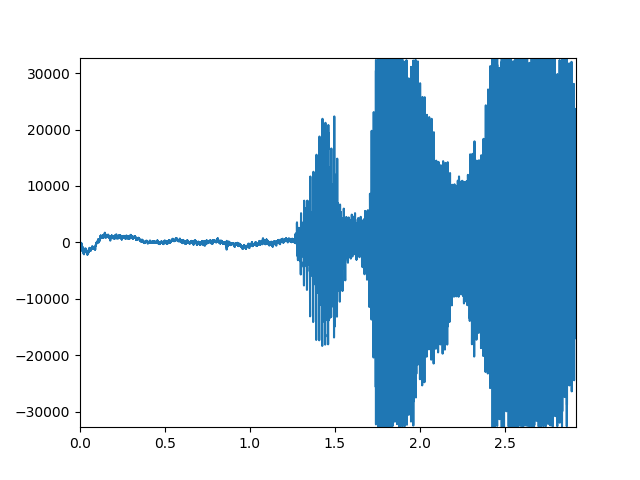
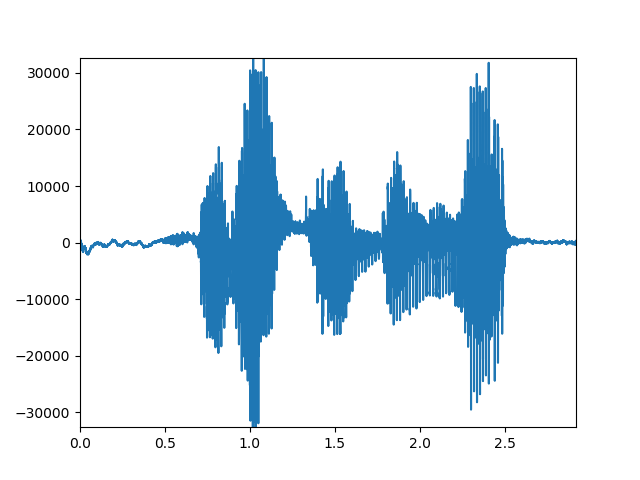
plt.plot(t, x)
plt.show()
f, t, Zxx = signal.stft(x, fs=fs*fn/20, nperseg=nperseg)
plt.figure()
plt.pcolormesh(t, f, np.abs(Zxx), vmin=0, vmax=amp)
plt.ylim([f[1], f[-1]])
plt.title('STFT Magnitude')
plt.ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
plt.yscale('log')
plt.show()
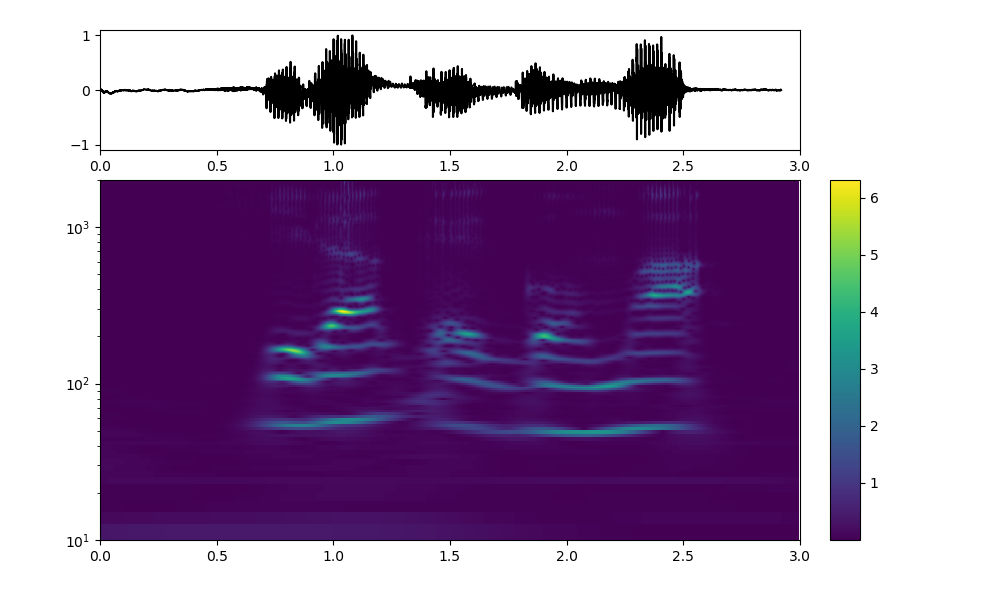
おはよう
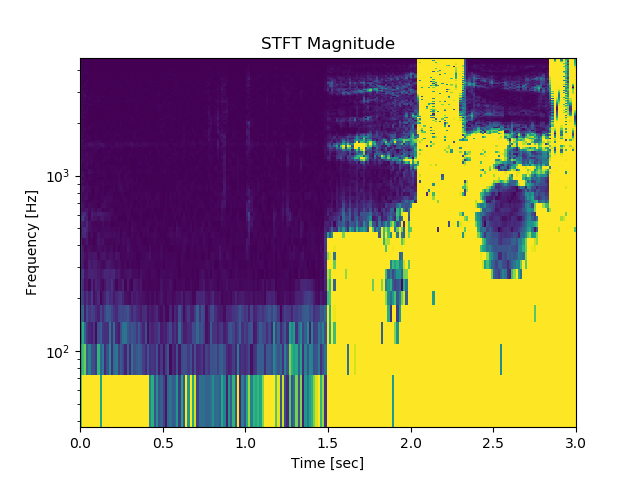
開けゴマ
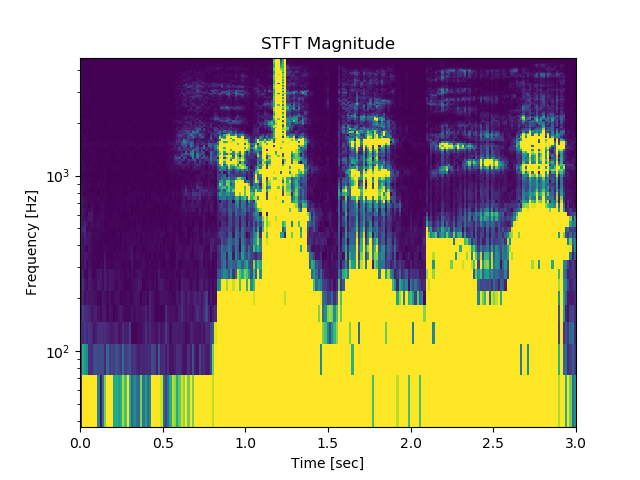
※残念ながら、横軸が今一つ正しくないようだが、現状リーズナブルな変数の組が見つからない。一方、縦軸の周波数はFFTの重なってる波形が時間軸で分離されている。大きさもだいたい正しいようだ。
# Zero the components that are 10% or less of the carrier magnitude, then convert back to a time series via inverse STFT
# キャリア振幅の10%以下の成分をゼロにしてから、逆STFTを介して時系列に変換し直す
# ⇒適当な条件でノイズ除去している
maxZxx= max(data)
print('maxZxx',maxZxx)
Zxx = np.where(np.abs(Zxx) >= maxZxx*2, Zxx, 0)
plt.figure()
plt.pcolormesh(t, f, np.abs(Zxx), vmin=0, vmax=amp)
plt.ylim([f[1], f[-1]])
plt.title('STFT Magnitude')
plt.ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
plt.yscale('log')
plt.show()
_, xrec = signal.istft(Zxx, fs)
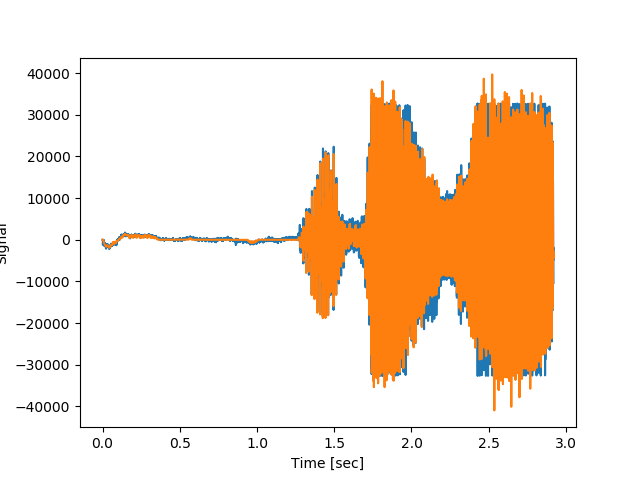
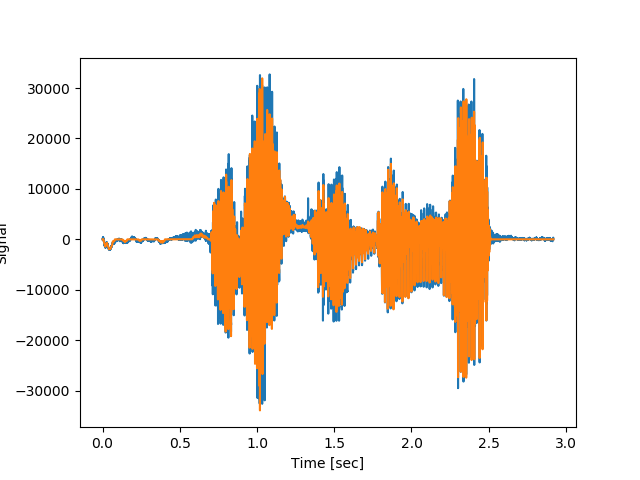
# Compare the cleaned signal with the original and true carrier signals.
# きれいにされた信号を元のそして本当の搬送波信号と比較
t = np.linspace(0,fs, fn/2, endpoint=False)
plt.figure()
plt.plot(t, x, t, xrec) #, time, carrier)
# plt.xlim([20, 75])
plt.xlabel('Time [sec]')
plt.ylabel('Signal')
# plt.legend(['Carrier + Noise', 'Filtered via STFT', 'True Carrier'])
plt.show()
plt.figure()
plt.plot(t, xrec-x) #, time, carrier)
# plt.xlim([0, 0.1])
plt.xlabel('Time [sec]')
plt.ylabel('Signal')
# plt.legend(['Carrier + Noise', 'Filtered via STFT', 'True Carrier'])
plt.show()
以下のとおり、wavファイルへの書き出しをやってみたが、上記の入力xそのまま書き出す場合は、綺麗な録音ができるが、逆変換したxrecは雑音がかなりのっている。
※ほとんど誤差がないので雑音が乗っかる理由はよくわからない
# 書き出し
outf = './output/test.wav'
ww = wave.open(outf, 'w')
ww.setnchannels(ch)
ww.setsampwidth(width)
ww.setframerate(fr)
outd = x #xrec
print(len(x))
ww.writeframes(outd)
ww.close()
以下のように、逆変換で戻したwavファイルのwidthやfrは以下のようにしないと間延びしていて、ノイズばかりでそれらしくも聞こえない
outf = './output/test1.wav'
ww = wave.open(outf, 'w')
ww.setnchannels(ch)
ww.setsampwidth(2*width)
ww.setframerate(2*fr)
maxrec=max(xrec)
outd = xrec/maxrec
print(max(outd),min(outd))
ww.writeframes(outd)
ww.close()
・wavelet変換・逆変換してみる;こちらも適当な窓関数について実行してみました
Scipy-Swan / swan_wavelet_wav.py
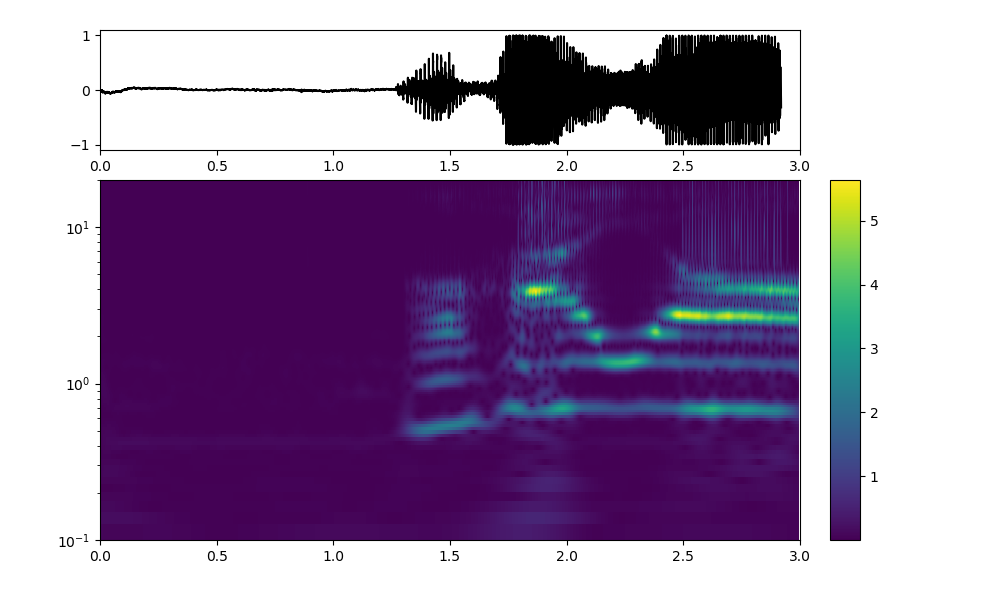
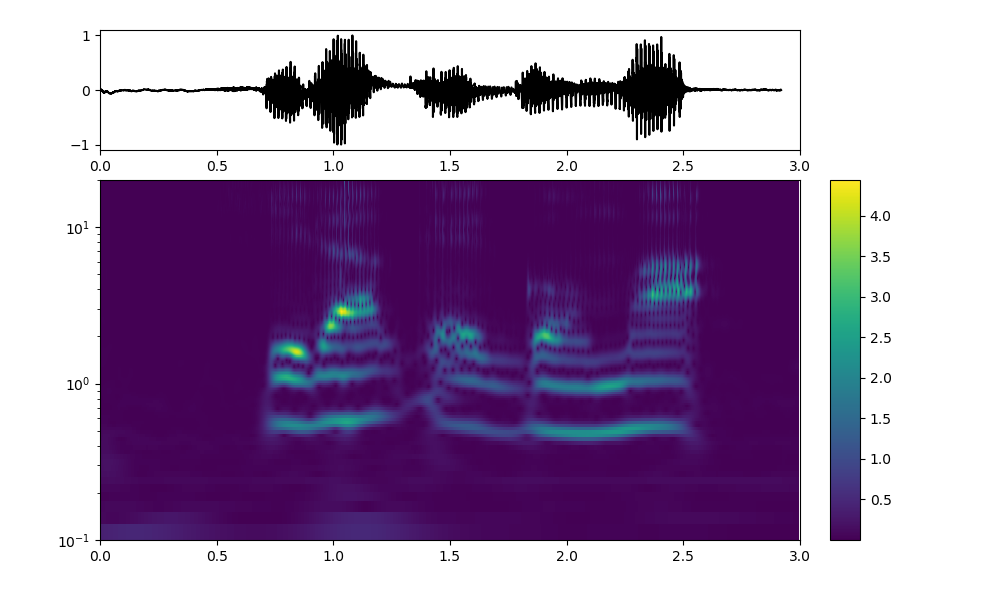
swan.cwtは変換も逆変換も時間軸はうまくできているように見えるが、縦軸の周波数の値がFFTなどと比較すると、二桁小さく出ている。
ただし、周波数の時間変化の全体的な振る舞いというか形状はstftと似ている。
from swan import pycwt
import numpy as np
import matplotlib.pyplot as plt
import wave
from scipy import fromstring, int16
wavfile = 'hirakegoma.wav'
# wavfile = 'ohayo.wav'
wr = wave.open(wavfile, "rb")
ch = wr.getnchannels()
width = wr.getsampwidth()
fr = wr.getframerate()
fn = wr.getnframes()
fs = fn / fr
print('ch', ch)
print('frame', fn)
print('fr',fr)
print('sampling fs ', fs, 'sec')
print('width', width)
origin = wr.readframes(wr.getnframes())
data = origin[:fn]
wr.close()
amp = max(data)
print(amp)
print('len of origin', len(origin))
print('len of sampling: ', len(data))
# ステレオ前提 > monoral
y = np.frombuffer(data, dtype="int16") /32768.0
x = np.linspace(0,fs, fn/2, endpoint=False)
plt.plot(x, y)
plt.show()
Fs = 1/0.01
omega0 = 2 #0.2 #1 #2 #8
# (1) Freqを指定してcwt
freqs=np.arange(0.1,20,0.025)
r=pycwt.cwt_f(y,freqs,Fs,pycwt.Morlet(omega0))
rr=np.abs(r)
plt.rcParams['figure.figsize'] = (10, 6)
fig = plt.figure()
ax1 = fig.add_axes([0.1, 0.75, 0.7, 0.2])
ax2 = fig.add_axes([0.1, 0.1, 0.7, 0.60], sharex=ax1)
ax3 = fig.add_axes([0.83, 0.1, 0.03, 0.6])
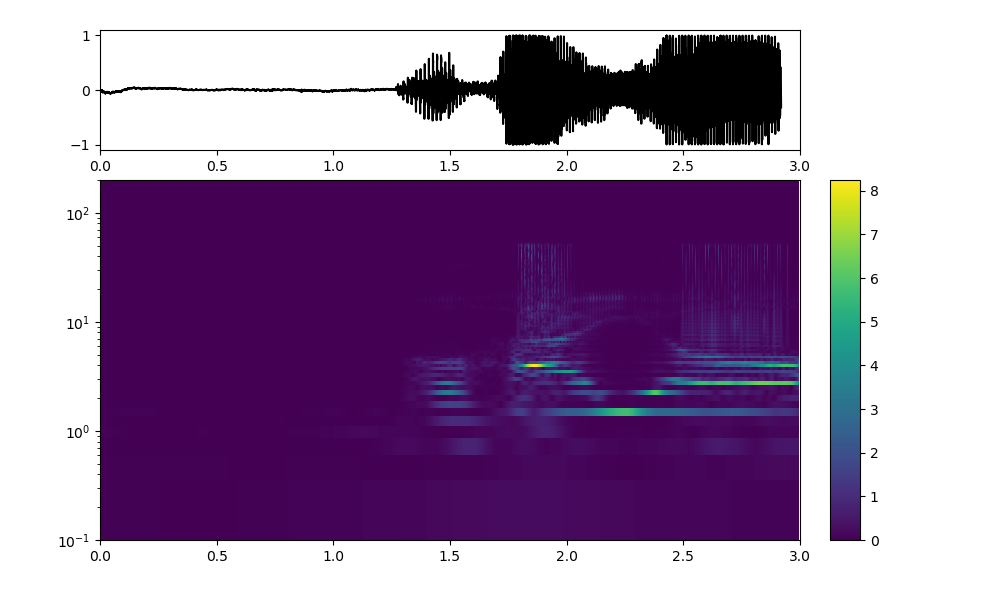
ax1.plot(x, y, 'k')
img = ax2.imshow(np.flipud(rr), extent=[0, 3,0.1, 20], aspect='auto')
twin_ax = ax2
twin_ax.set_yscale('log')
twin_ax.set_xlim(0, 3)
twin_ax.set_ylim(0.1, 20)
ax2.tick_params(which='both', labelleft=False, left=False)
twin_ax.tick_params(which='both', labelleft=True, left=True, labelright=False)
fig.colorbar(img, cax=ax3)
plt.show()
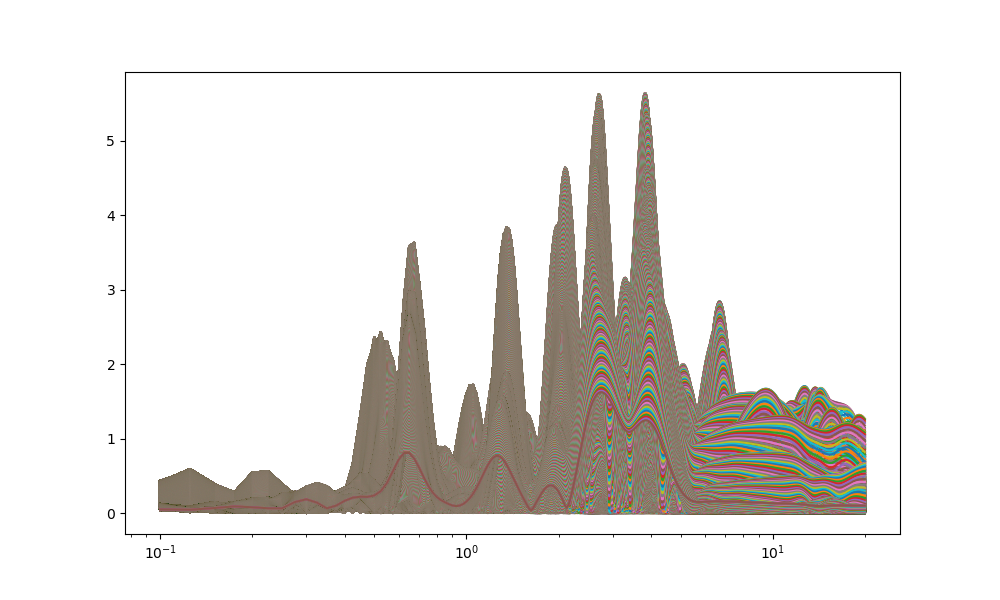
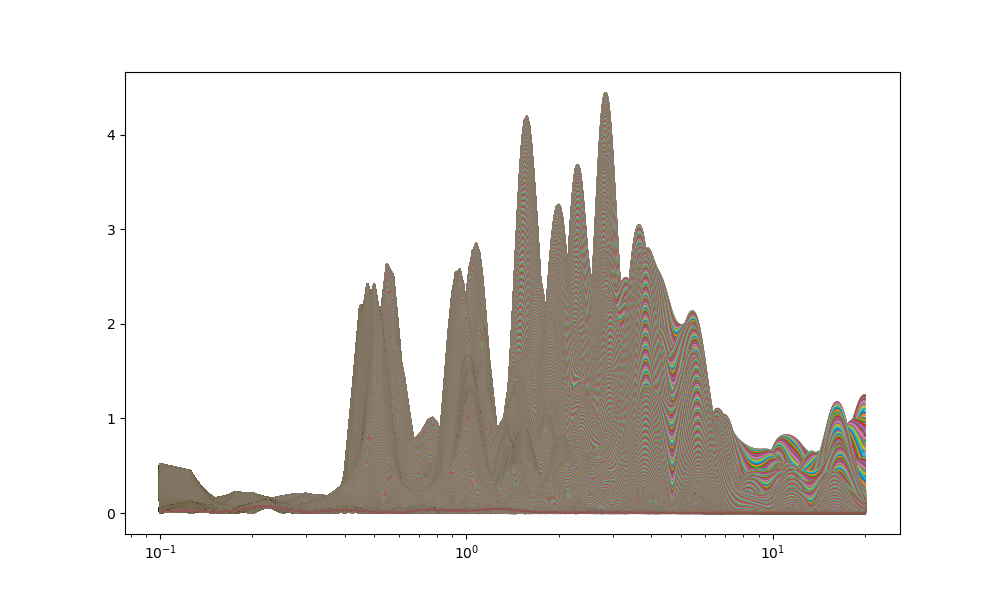
plt.plot(freqs,rr)
plt.xscale('log')
plt.show()
縦軸の周波数が酷く小さく出ているが、出力範囲を以下のように変更してもあまり変化しない、、、
Fs = 1/0.01
omega0 = 5 #0.2 #1 #2 #8 #ここを変更
# (1) Freqを指定してcwt
freqs=np.arange(0.1,200,0.25) #ここを変更
r=pycwt.cwt_f(y,freqs,Fs,pycwt.Morlet(omega0))
rr=np.abs(r)
plt.rcParams['figure.figsize'] = (10, 6)
fig = plt.figure()
ax1 = fig.add_axes([0.1, 0.75, 0.7, 0.2])
ax2 = fig.add_axes([0.1, 0.1, 0.7, 0.60], sharex=ax1)
ax3 = fig.add_axes([0.83, 0.1, 0.03, 0.6])
ax1.plot(x, y, 'k')
# 以下のy軸の範囲200に変更
img = ax2.imshow(np.flipud(rr), extent=[0, 3,0.1, 200], aspect='auto') #, interpolation='nearest')
twin_ax = ax2
twin_ax.set_yscale('log')
twin_ax.set_xlim(0, 3)
twin_ax.set_ylim(0.1, 200) #ここを変更
ax2.tick_params(which='both', labelleft=False, left=False)
twin_ax.tick_params(which='both', labelleft=True, left=True, labelright=False)
fig.colorbar(img, cax=ax3)
plt.show()
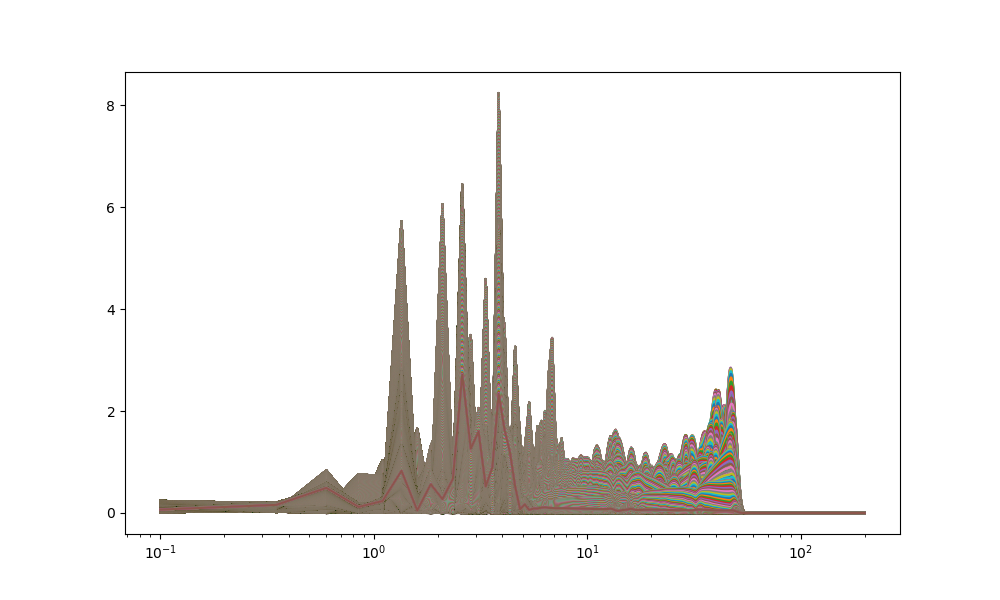
plt.plot(freqs,rr)
plt.xscale('log')
plt.show()
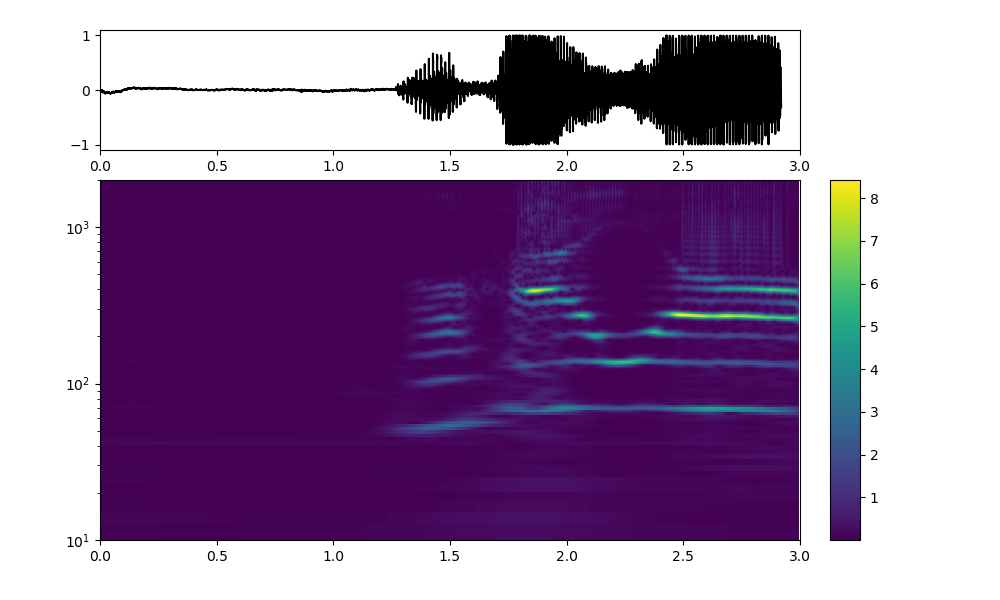
そして、周波数の係数Fs = 1/0.0001まで大きくすると、以下のとおり、周波数の範囲もやっとFFTとほぼ似たような値に近づいた。
※これはき基準周波数を測定して校正する必要があることを意味する
Fs = 1/0.0001
omega0 = 5 #0.2 #1 #2 #8
# (1) Freqを指定してcwt
freqs=np.arange(10,2000,2.5)
r=pycwt.cwt_f(y,freqs,Fs,pycwt.Morlet(omega0))
rr=np.abs(r)
plt.rcParams['figure.figsize'] = (10, 6)
fig = plt.figure()
ax1 = fig.add_axes([0.1, 0.75, 0.7, 0.2])
ax2 = fig.add_axes([0.1, 0.1, 0.7, 0.60], sharex=ax1)
ax3 = fig.add_axes([0.83, 0.1, 0.03, 0.6])
ax1.plot(x, y, 'k')
img = ax2.imshow(np.flipud(rr), extent=[0, 3,10, 2000], aspect='auto') #, interpolation='nearest')
twin_ax = ax2
twin_ax.set_yscale('log')
twin_ax.set_xlim(0, 3)
twin_ax.set_ylim(10, 2000)
ax2.tick_params(which='both', labelleft=False, left=False)
twin_ax.tick_params(which='both', labelleft=True, left=True, labelright=False)
fig.colorbar(img, cax=ax3)
plt.show()
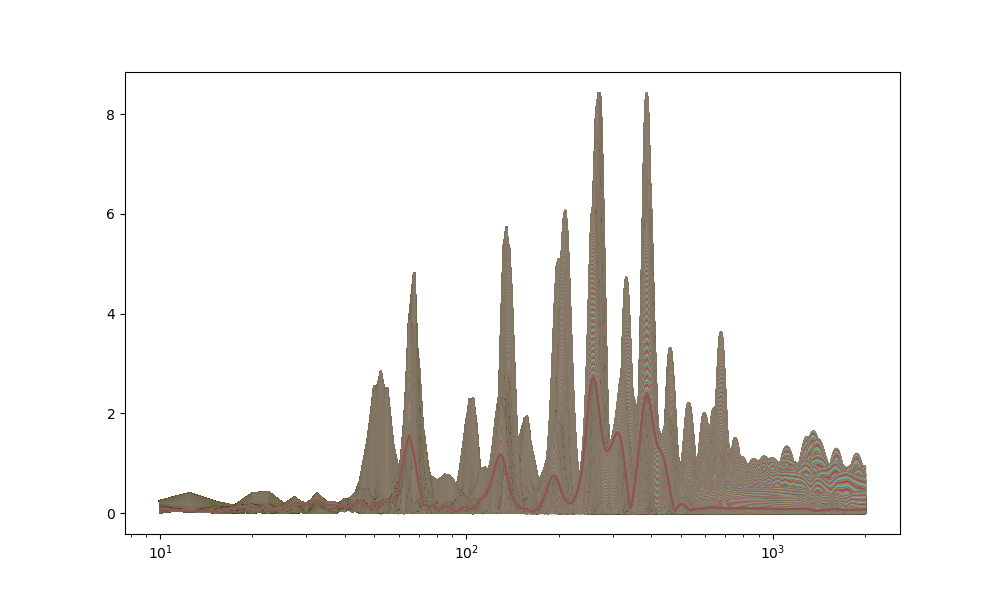
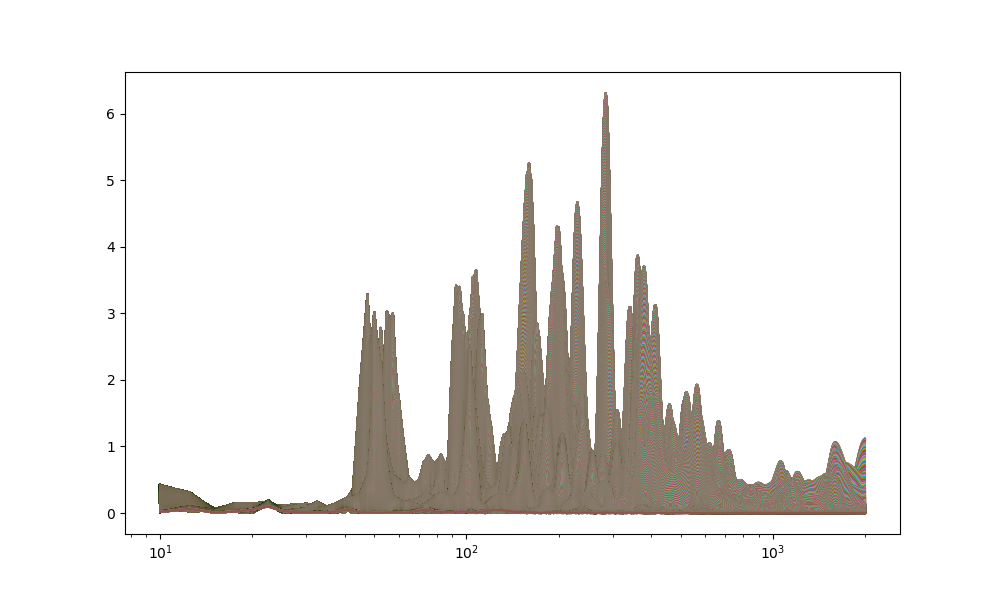
plt.plot(freqs,rr)
plt.xscale('log')
plt.show()
まとめ
・「おはよう」「開けゴマ」という実音声データ(wavデータ)について、FFT、STFT及びwavelet変換を行った
・FFTは校正無しで、時間軸の変化は見えないものの、全体としてどのあたりの周波数にピークが出ているかわかりやすい
・STFTは大体の周波数ー時間空間でのスペクトログラムを描いているが、今回は横軸が必ずしもリーズナブルに決定することが出来なかった
・Wavelet変換は、周波数ー時間空間でのスペクトログラムを示すが、周波数軸に関して校正が必要なようである
・次回は、少しだけ理論を振り返って、理論的な理解を補い、これまでに得た漠然とした知識を確固なものにしたいと思う。