今夜は予定通り、「FFT、STFT、そしてWavelet変換における②不確定性原理」について実際の計算を通して考える。
とりあえずの目標
以下のとおり、
※リンクされているものは記事にしたものであり、その記事を前提知識として書いて行くので、参照すると理解し易いと思います。
①Scipy環境を作る
・環境の確認
②不確定原理について
・FFT変換・逆変換してみる;時間軸が消える
・STFT変換・逆変換してみる;窓関数について
・wavelet変換・逆変換してみる;スペクトログラムの解釈と不確定原理
③音声や地震データや株価や、。。。とにかく一次元の実時系列データに応用する
④FFTからwavelet変換まで簡単にたどってみる(上記以外のちょっと理論)
⑤二次元データに応用してみる
⑥天体観測データに応用してみる
⑦リアルタイムにスペクトログラムしてみる
今回やったこと
②不確定原理について
・FFT変換・逆変換してみる;時間軸が消える
・STFT変換・逆変換してみる;窓関数について
・wavelet変換・逆変換してみる;スペクトログラムの解釈と不確定原理
・FFT変換・逆変換してみる;時間軸が消える
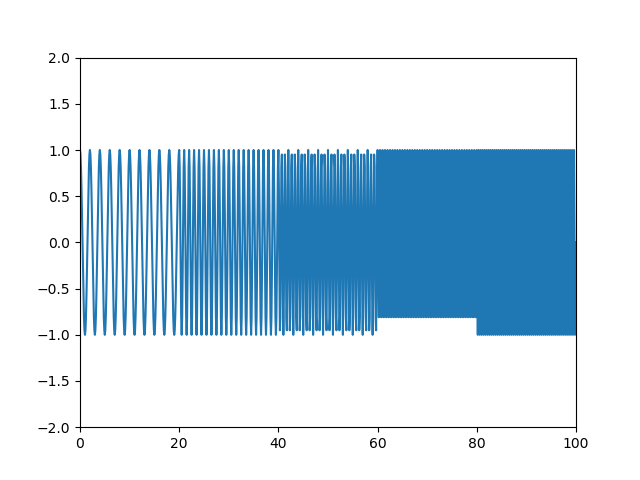
今回の入力の波形は、一定時間ごとにシステマティックに周期が変化するものを使う。
FFTに関しては、時間軸全体で積分してしまうので、当然ながら周波数の時間的な変化は出ない。
コードは以下のとおり
from scipy.fftpack import fft, ifft
import numpy as np
import matplotlib.pyplot as plt
以下のように時間的に変化する関数を使う。
t = np.linspace(0, 100, 1000, endpoint=False)
sig=[]
for t1 in t:
if t1<20:
sig1 = np.cos(2 * np.pi * 0.5 * t1)
print("5",t1)
elif t1<40:
sig1 = np.cos(2 * np.pi * 1 * t1)
print("10",t1)
elif t1<60:
sig1 = np.cos(2 * np.pi * 1.5 * t1)
print("20",t1)
elif t1<80:
sig1 = np.cos(2 * np.pi * 2 * t1)
print("30",t1)
else:
sig1 = np.cos(2 * np.pi * 2.5 * t1)
print(t1)
sig.append(sig1)
plt.plot(t, sig)
plt.axis([0, 100, -2, 2])
plt.show()
これを以下のようにFFTすると、当然ながら入力波形の周波数(50,100,150,200,250)のところにピークが出現する。
freq =fft(sig,1024)
Pyy = np.sqrt(freq*freq.conj())/1025 #np.abs(freq)/1025
f = np.arange(1024)
plt.plot(f,Pyy)
plt.axis([0, 512, 0, 0.2])
plt.show()
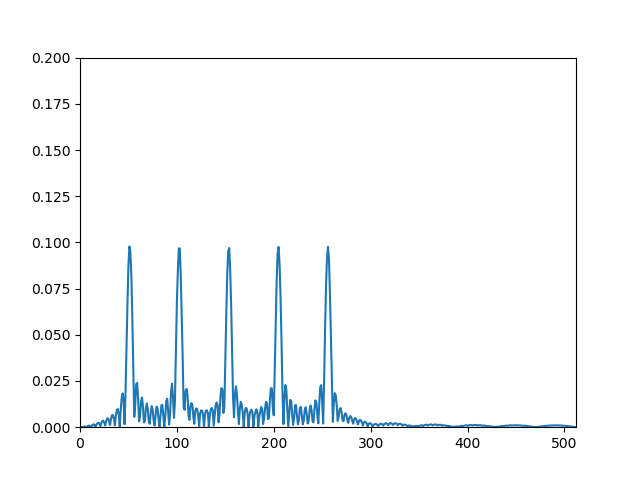
そして、逆FFTを行うと、以下のとおりみごとに元の波形に戻る。
t1=np.linspace(0, 100, 1024, endpoint=False)
sig1=ifft(freq)
plt.plot(t1, sig1)
plt.axis([0, 100, -2, 2])
plt.show()
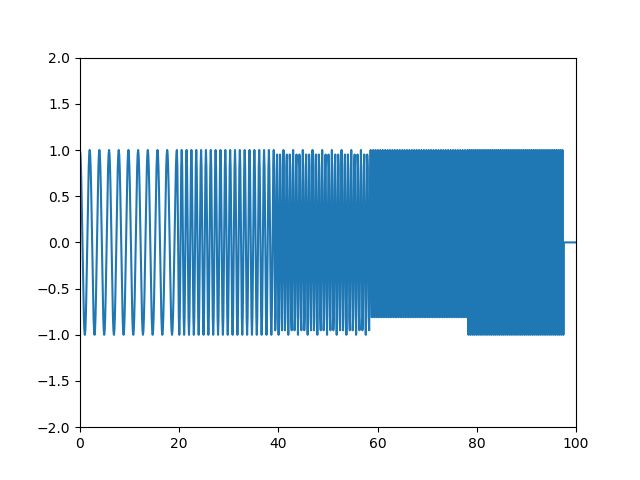
ここで注意したいのは、最後のしっぽが完全には戻らないことである。
以上のとおり、FFTにおける不確定性原理は、時間軸から変換の共役変数である周波数軸に完全に移り、変換の前後で以前の空間の情報は完全に失われることである。
・STFT変換・逆変換してみる;窓関数について
STFTでは、時間的に変換する範囲を窓関数を乗ずることにより小時間単位にFFTを実施することにより、周波数分布(スペクトル)の時間的な変化の観察を実現している。
【参考】
・短時間フーリエ変換@Wikipedia
参考によれば、窓関数の時間的な幅を変化することにより、不確定性原理が見えるということなので、これを見たいと思う。
コードは以下の通りである。
# scipy.signal.istft example
# https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.istft.html
#
import numpy as np #added by author
from scipy import signal
import matplotlib.pyplot as plt
# Generate a test signal, a 2 Vrms sine wave at 50Hz corrupted by 0.001 V**2/Hz of white noise sampled at 1024 Hz.
# テスト信号、1024 Hzでサンプリングされた0.001 V ** 2 / Hzのホワイトノイズで破損した50 Hzの2 Vrmsの正弦波を生成します
fs = 1024
N = 10*fs
以下のnperseq変数の値を変更すると、窓関数の時間幅を変更することができる。
nperseg = 64 #2048 #1024 #128 #256 #512
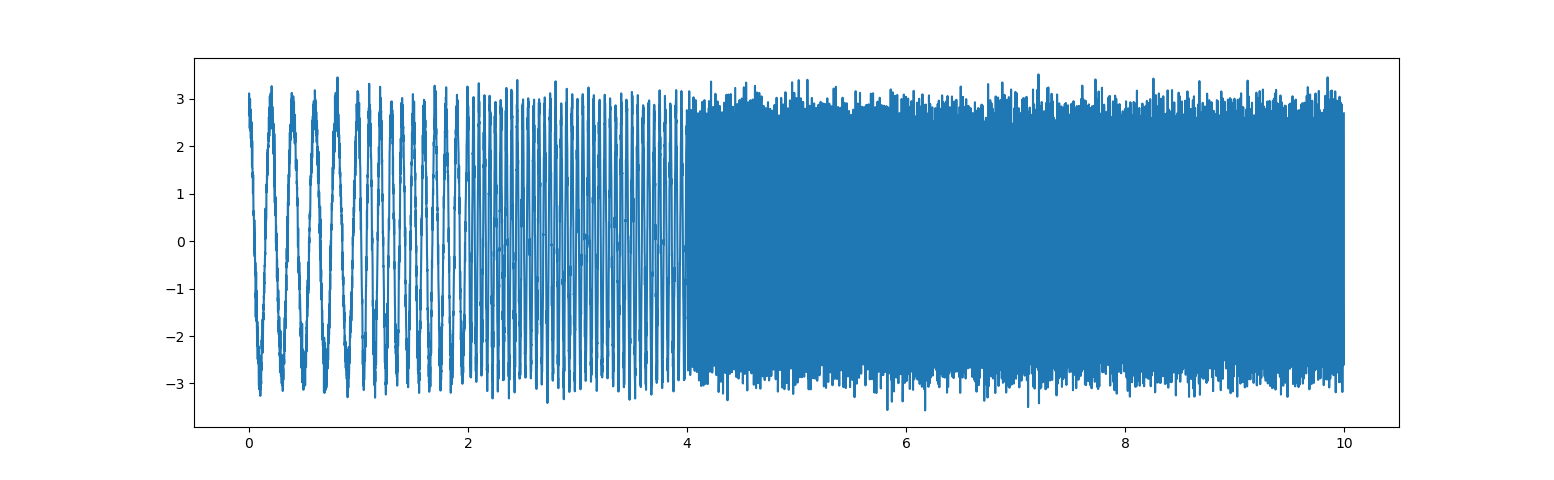
入力波形の関数をFFTのときと同一にする。
一応、ノイズは当初のものを利用し、ノイズ除去ができるところも見る。
amp = 2 * np.sqrt(2)
noise_power = 0.0001 * fs / 2
time = np.arange(N) / float(fs)
# carrier = amp * np.sin(2*np.pi*50*time)
# t = np.linspace(0, 100, 1000, endpoint=False)
carrier=[]
for t1 in time:
if t1<1:
sig1 = amp*np.cos(2 * np.pi * 5 * t1) #+np.cos(2 * np.pi * 8 * t) + np.cos(2 * np.pi * 15 * t) #*np.exp(-0.1*t) *5
print("5",t1)
elif t1<2:
sig1 = amp*np.cos(2 * np.pi * 10 * t1)
print("10",t1)
elif t1<4:
sig1 = amp*np.cos(2 * np.pi * 20 * t1)
print("20",t1)
elif t1<6:
sig1 = amp*np.cos(2 * np.pi * 50 * t1)
print("30",t1)
else:
sig1 = amp*np.cos(2 * np.pi * 100 * t1)
print(t1)
carrier.append(sig1)
noise = np.random.normal(scale=np.sqrt(noise_power),
size=time.shape)
x = carrier + noise
# Compute and plot the STFT’s magnitude.
# STFTの振幅を計算してプロットします
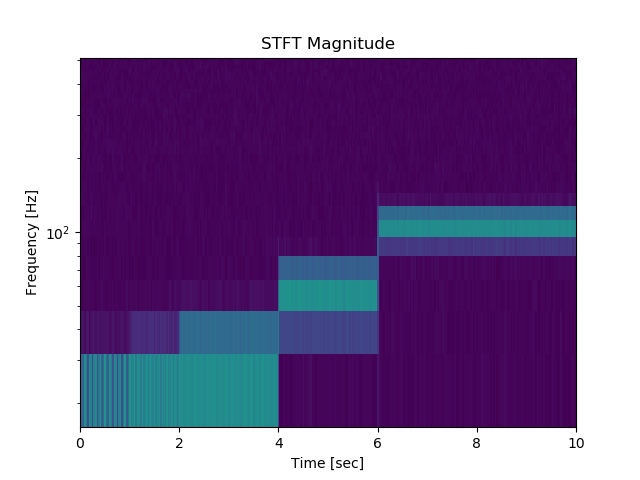
f, t, Zxx = signal.stft(x, fs=fs, nperseg=nperseg)
plt.figure()
plt.pcolormesh(t, f, np.abs(Zxx), vmin=0, vmax=amp)
plt.ylim([f[1], f[-1]])
plt.title('STFT Magnitude')
plt.ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
plt.yscale('log')
plt.show()
npersegの値を変化させたときの周波数の時間依存性は以下のとおりとなる。
まさしく、Wikipediaに記載されている通りの事象が発生する。
これが、STFTにおける不確定性原理と呼ばれる現象である。
すなわち、窓の時間的な広がりが大きければ求められる周波数の広がりは狭まり、逆に時間的な遷移領域(重なり領域)が大きくなる現象である。
※理論的な話は別途あとで扱うこととし、ここでは言及しない
2048
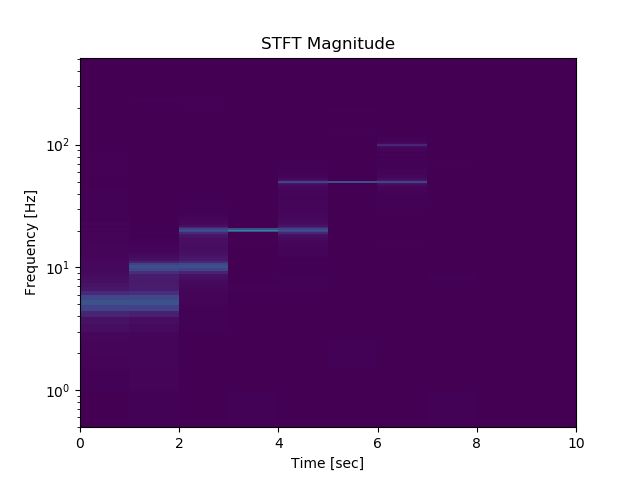
1024
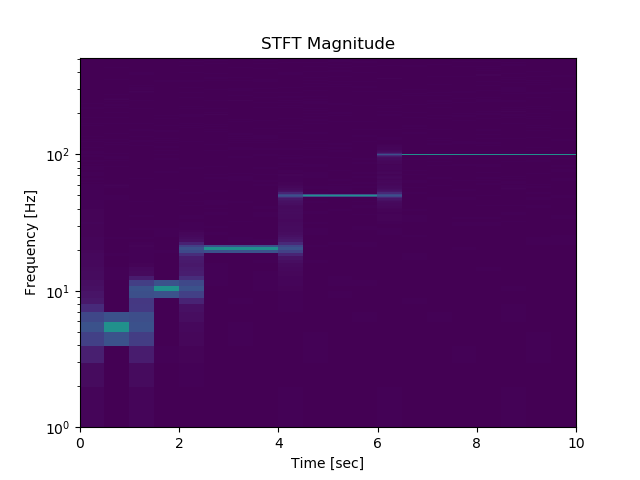
512
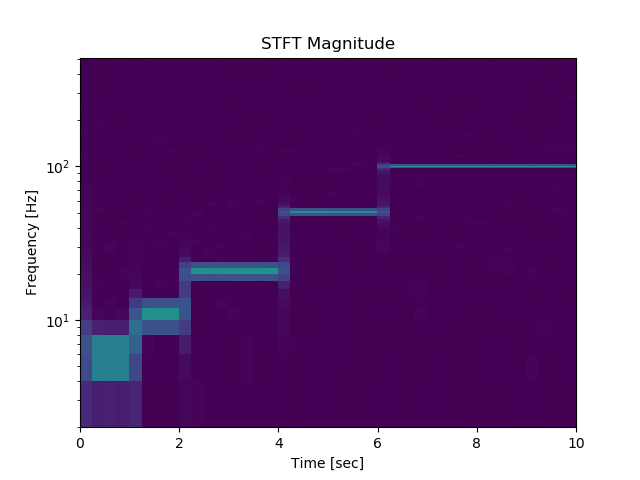
256
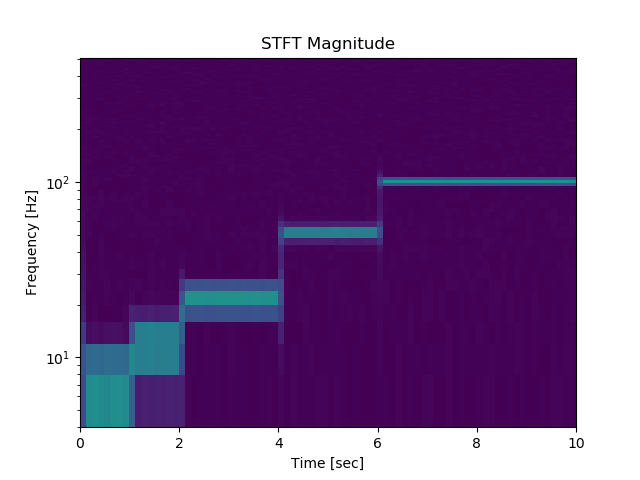
128
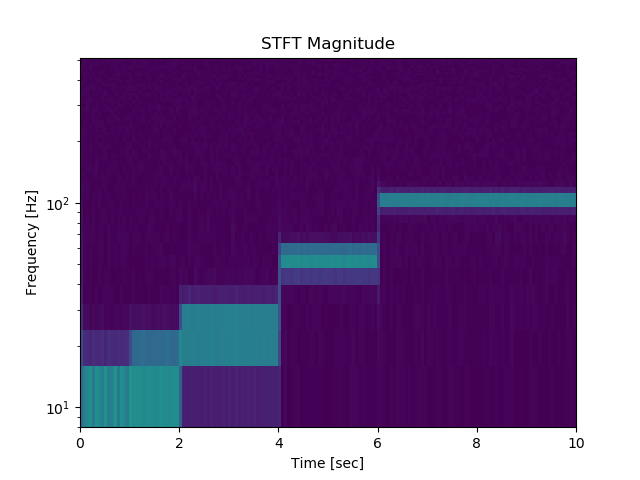
64
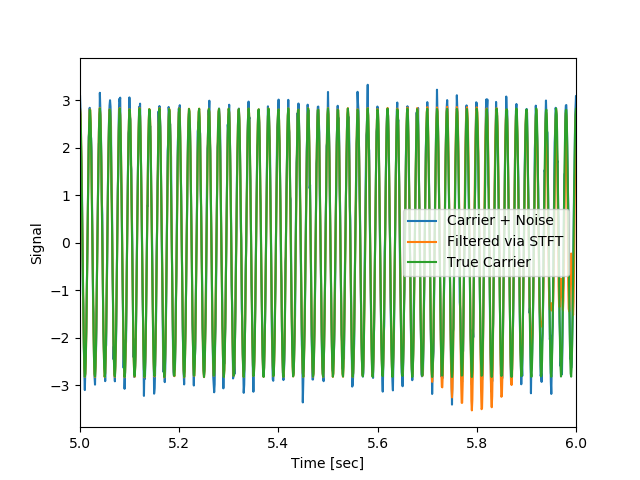
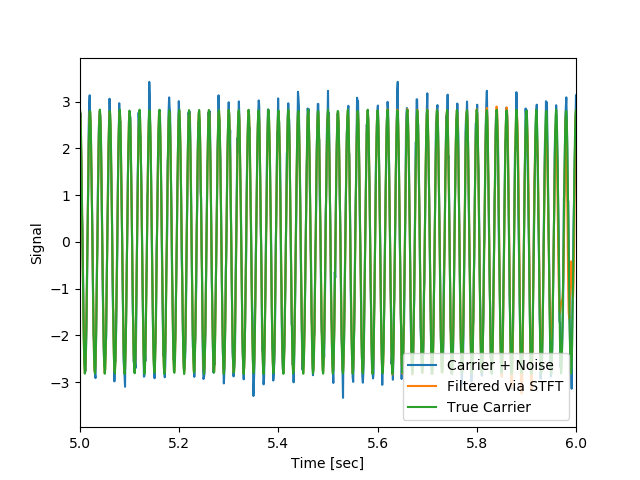
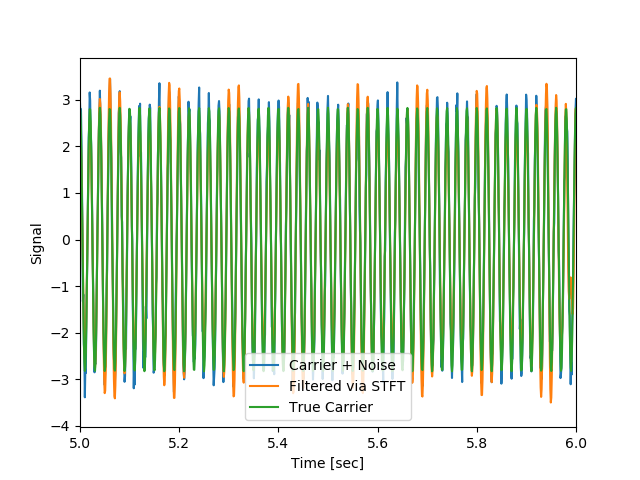
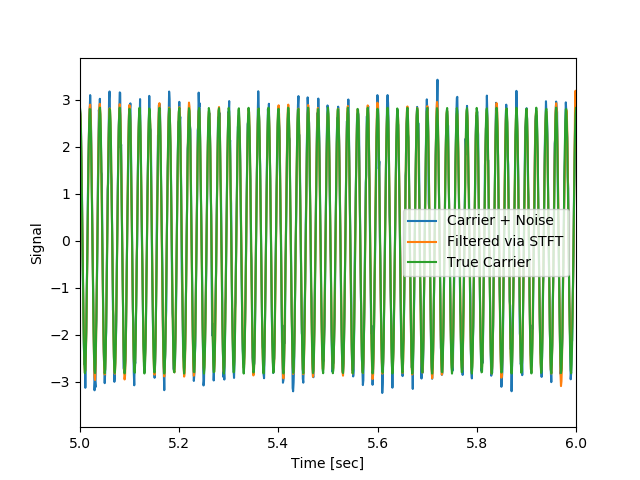
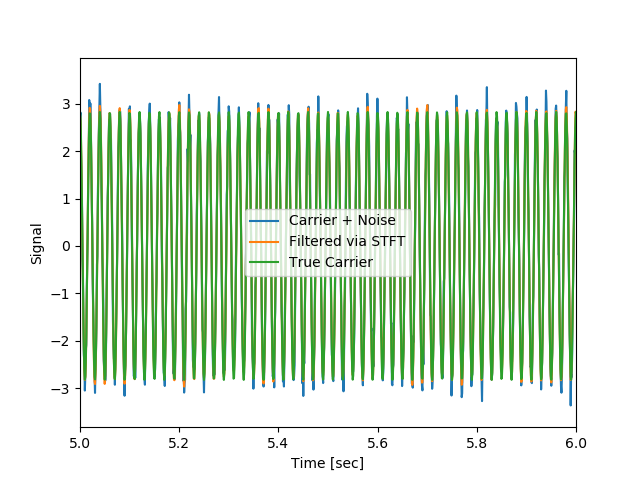
そして、逆変換することにより、元に戻る様子を以下で見る。
実は、これは窓関数に依存せず、すべてのケースで元波形(ノイズが除去されたもの)が得られた。ただし、境界領域や立ち上がりなどは異なることが分かる。
# Zero the components that are 10% or less of the carrier magnitude, then convert back to a time series via inverse STFT
# キャリア振幅の10%以下の成分をゼロにしてから、逆STFTを介して時系列に変換し直す
Zxx = np.where(np.abs(Zxx) >= amp/10, Zxx, 0)
_, xrec = signal.istft(Zxx, fs)
# Compare the cleaned signal with the original and true carrier signals.
# きれいにされた信号を元のそして本当の搬送波信号と比較
plt.figure()
plt.plot(time, x, time, xrec, time, carrier)
plt.xlim([5, 6])
plt.xlabel('Time [sec]')
plt.ylabel('Signal')
plt.legend(['Carrier + Noise', 'Filtered via STFT', 'True Carrier'])
plt.show()
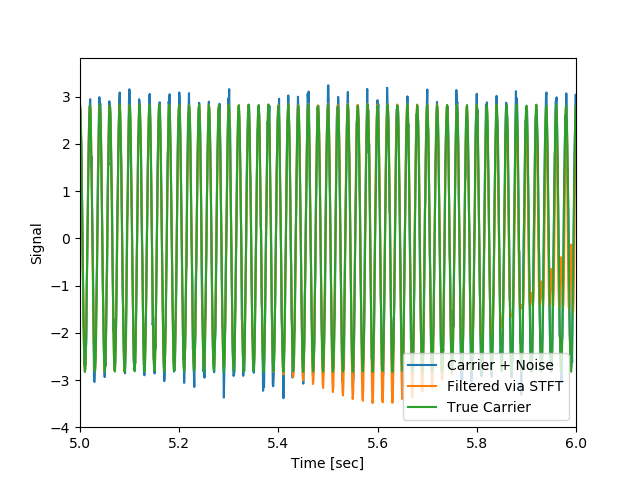
# Note that the cleaned signal does not start as abruptly as the original, since some of the coefficients of the transient were also removed:
# トランジェントの係数の一部も削除されているため、クリーン化された信号は元の信号ほど急激には開始されません。
plt.figure()
plt.plot(time, x, time, xrec, time, carrier)
plt.xlim([0, 1])
plt.xlabel('Time [sec]')
plt.ylabel('Signal')
plt.legend(['Carrier + Noise', 'Filtered via STFT', 'True Carrier'])
plt.show()
2048;立ち上がりが大きくずれている
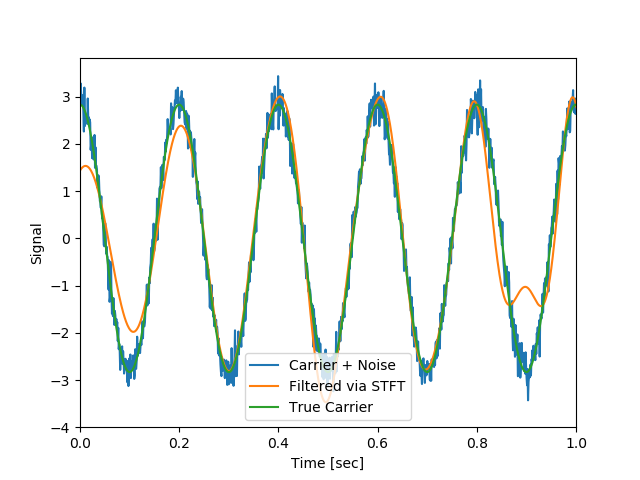
1024
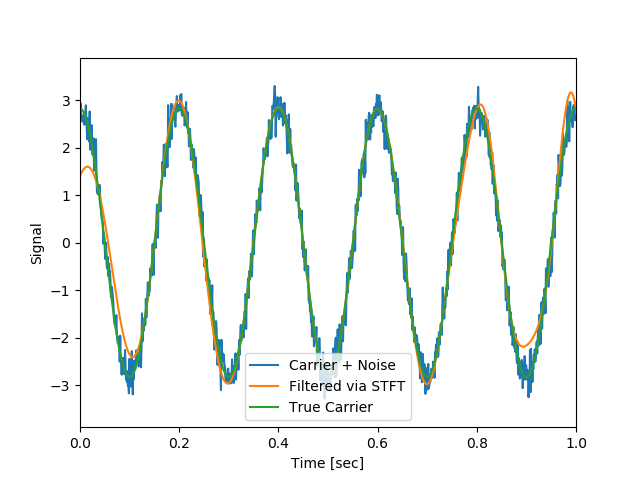
512
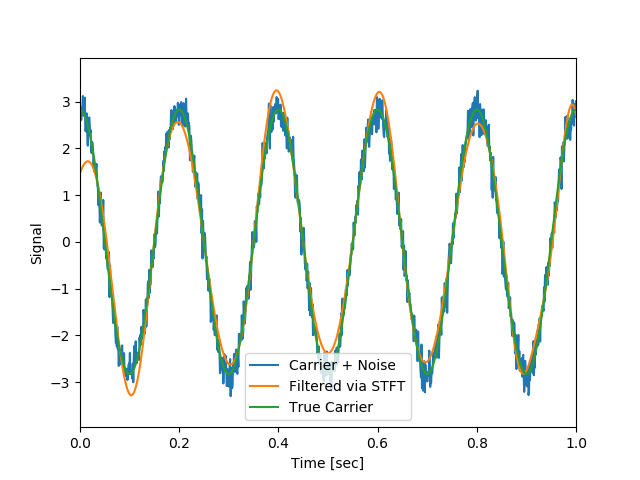
256
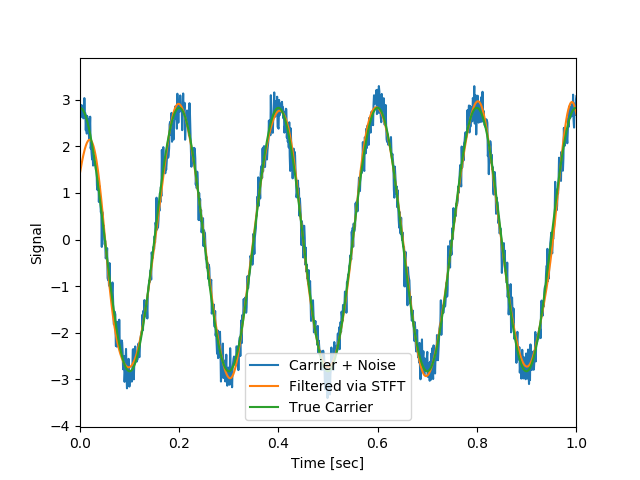
128;ほんの少しずれが発生している
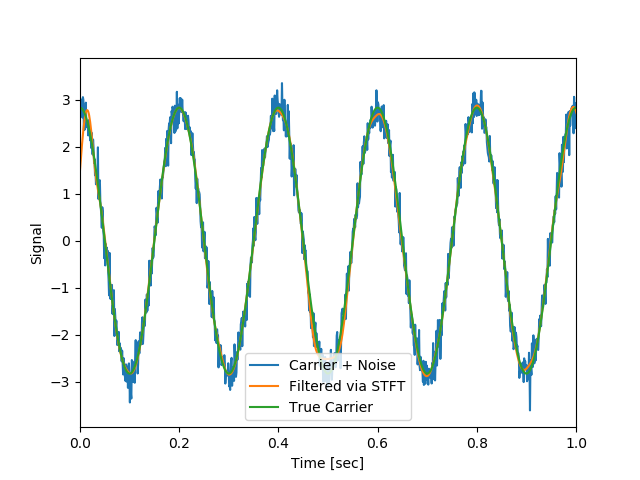
64;実は立ち上がりも綺麗に始まっているのがわかる
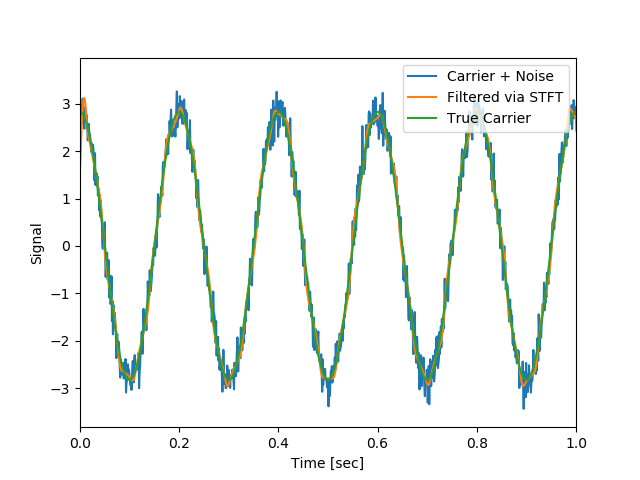
・wavelet変換・逆変換してみる;スペクトログラムの解釈と不確定原理
Waveletは若干手間取った。というか、参考でも記述されているが、Scipy.signal.cwtはどうもパラメータ変更ができないので、仕方なく参考の例からswan.cwtを利用することとした。
【参考】
・Pythonで連続ウェーブレット変換(scipy, mlpy, swan)
まず、普通の関数で綺麗に周波数に分離できることを見る。
from swan import pycwt
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0, 20, 0.01)
y = np.sin(2 * np.pi * 2 * x) * 2 + np.sin(2 * np.pi * 5 * x) * 2 + np.sin(2 * np.pi * 10 * x)
plt.plot(x, y)
plt.show()
Fs = 1/0.01
omega0 = 8
# (1) Freqを指定してcwt
freqs=np.arange(0.1,20,0.025)
r=pycwt.cwt_f(y,freqs,Fs,pycwt.Morlet(omega0))
rr=np.abs(r)
plt.rcParams['figure.figsize'] = (10, 6)
fig = plt.figure()
ax1 = fig.add_axes([0.1, 0.75, 0.7, 0.2])
ax2 = fig.add_axes([0.1, 0.1, 0.7, 0.60], sharex=ax1)
ax3 = fig.add_axes([0.83, 0.1, 0.03, 0.6])
ax1.plot(x, y, 'k')
img = ax2.imshow(np.flipud(rr), extent=[0, 20,0.1, 20], aspect='auto') #, interpolation='nearest')
twin_ax = ax2
twin_ax.set_yscale('log')
twin_ax.set_xlim(0, 20)
twin_ax.set_ylim(0.1, 20)
ax2.tick_params(which='both', labelleft=False, left=False)
twin_ax.tick_params(which='both', labelleft=True, left=True, labelright=False)
fig.colorbar(img, cax=ax3)
plt.show()
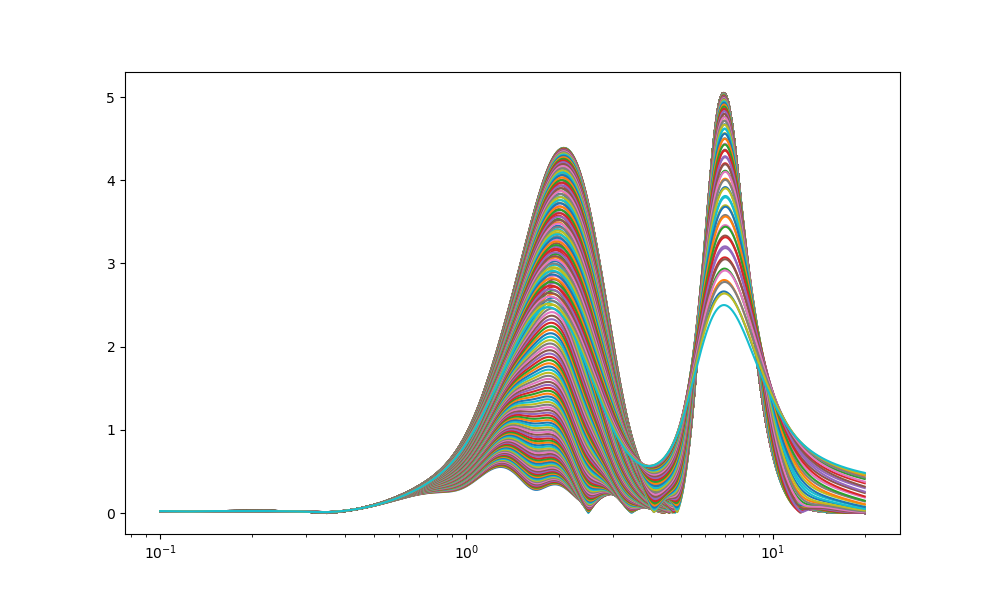
plt.plot(freqs,rr)
plt.xscale('log')
plt.show()
ということで、不確定性原理が出現するかどうを見る。
コードは以下の通り
from swan import pycwt
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0, 20, 0.01)
# y = np.sin(2 * np.pi * 2 * x) * 2 + np.sin(2 * np.pi * 5 * x) * 2 + np.sin(2 * np.pi * 10 * x)
amp=1
y=[]
for t1 in x:
if t1<3:
sig1 = amp*np.cos(2 * np.pi * 0.5 * t1) #+np.cos(2 * np.pi * 8 * t) + np.cos(2 * np.pi * 15 * t) #*np.exp(-0.1*t) *5
elif t1<8:
sig1 = amp*np.cos(2 * np.pi * 4 * t1)
elif t1<12:
sig1 = amp*np.cos(2 * np.pi * 7 * t1)
elif t1<15:
sig1 = amp*np.cos(2 * np.pi * 12 * t1)
else:
sig1 = amp*np.cos(2 * np.pi * 15 * t1)
y.append(sig1)
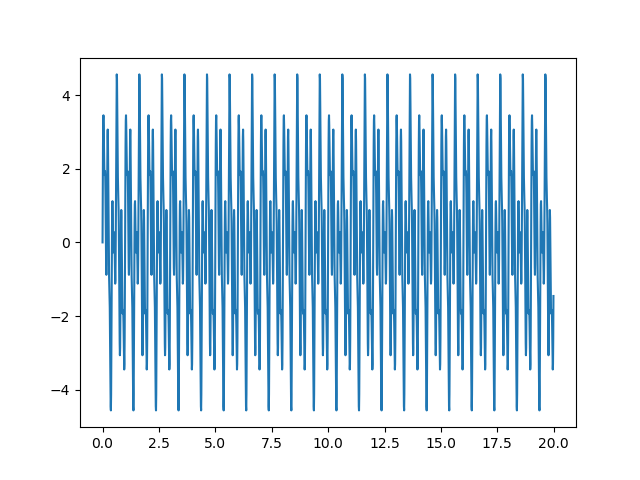
plt.plot(x, y)
plt.show()
Fs = 1/0.01
omega0 = 0.2 #1 #2 #8
# (1) Freqを指定してcwt
freqs=np.arange(0.1,20,0.025)
r=pycwt.cwt_f(y,freqs,Fs,pycwt.Morlet(omega0))
rr=np.abs(r)
plt.rcParams['figure.figsize'] = (10, 6)
fig = plt.figure()
ax1 = fig.add_axes([0.1, 0.75, 0.7, 0.2])
ax2 = fig.add_axes([0.1, 0.1, 0.7, 0.60], sharex=ax1)
ax3 = fig.add_axes([0.83, 0.1, 0.03, 0.6])
ax1.plot(x, y, 'k')
img = ax2.imshow(np.flipud(rr), extent=[0, 20,0.1, 20], aspect='auto') #, interpolation='nearest')
twin_ax = ax2
twin_ax.set_yscale('log')
twin_ax.set_xlim(0, 20)
twin_ax.set_ylim(0.1, 20)
ax2.tick_params(which='both', labelleft=False, left=False)
twin_ax.tick_params(which='both', labelleft=True, left=True, labelright=False)
fig.colorbar(img, cax=ax3)
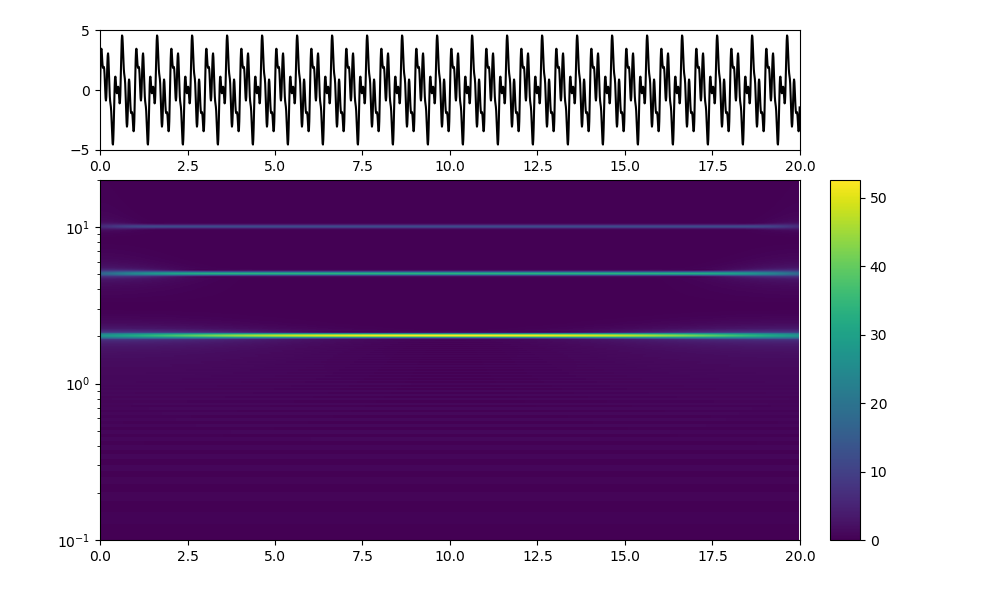
plt.show()
一目見てわかるように、不確定性原理の現象が起こっている。
omega0=8;時間軸がぼけぼけで境界が曖昧、特に低周波が酷い
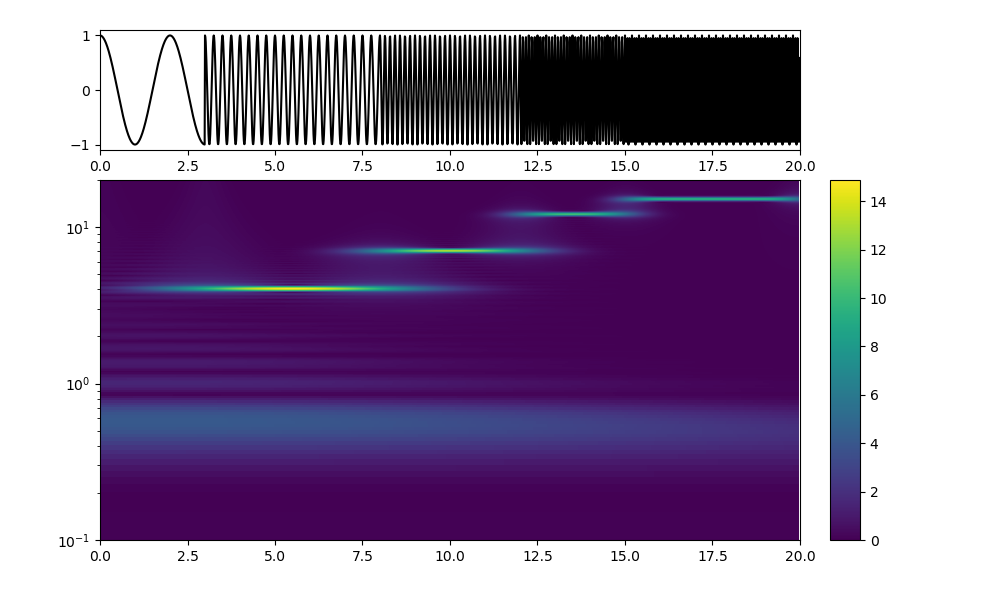
時間軸の曖昧さは明らかに小さくなっている。
omega0=2;時間軸のぼけが収まってきた、特に低周波の時間領域がまとまりだした
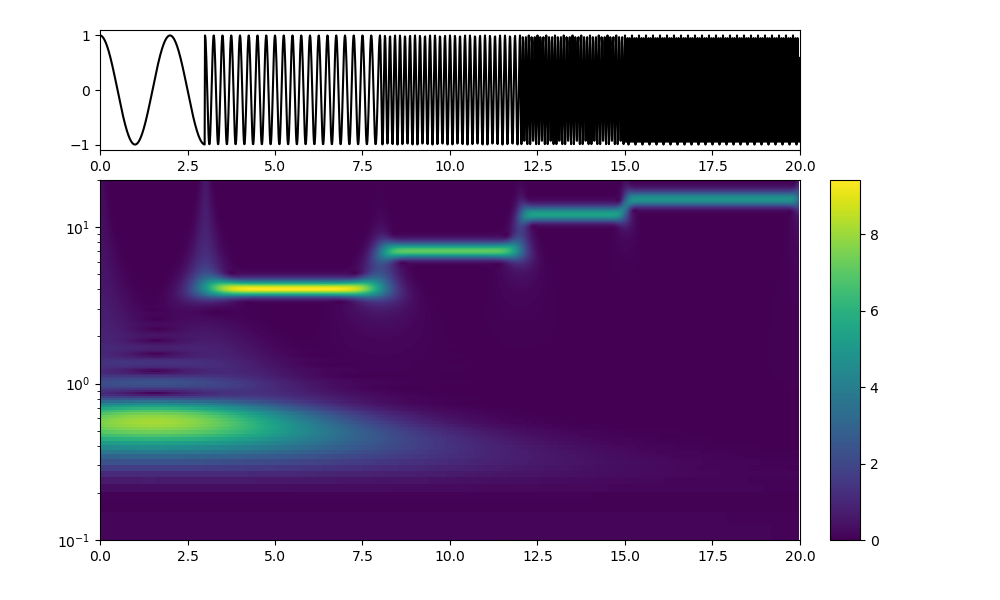
omega0=1;時間軸のぼけがかなり収まったが、周波数のバンド化が酷くなった
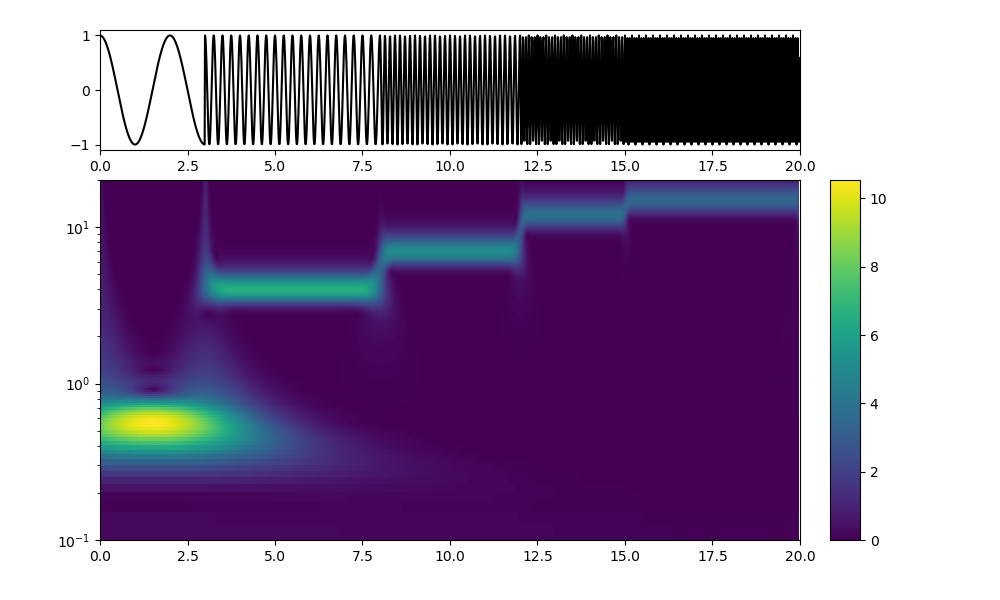
omega0=0.5;周波数のバンド化がさらに酷くなった、
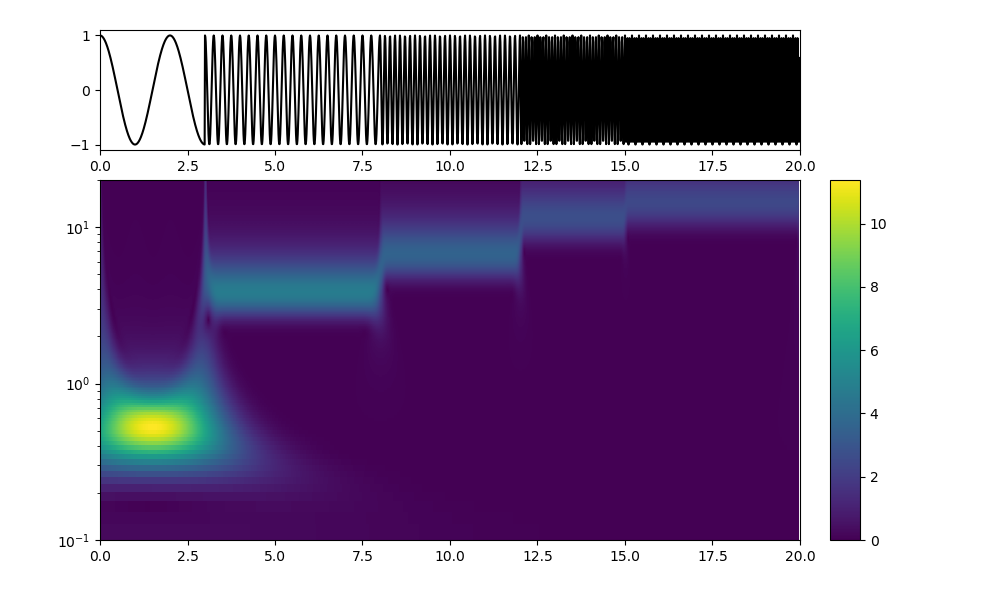
omega0=0.2;周波数のバンドがさらに広がりピークが見えなくなった、時間軸の周波数の移り変わりははっきりしている。
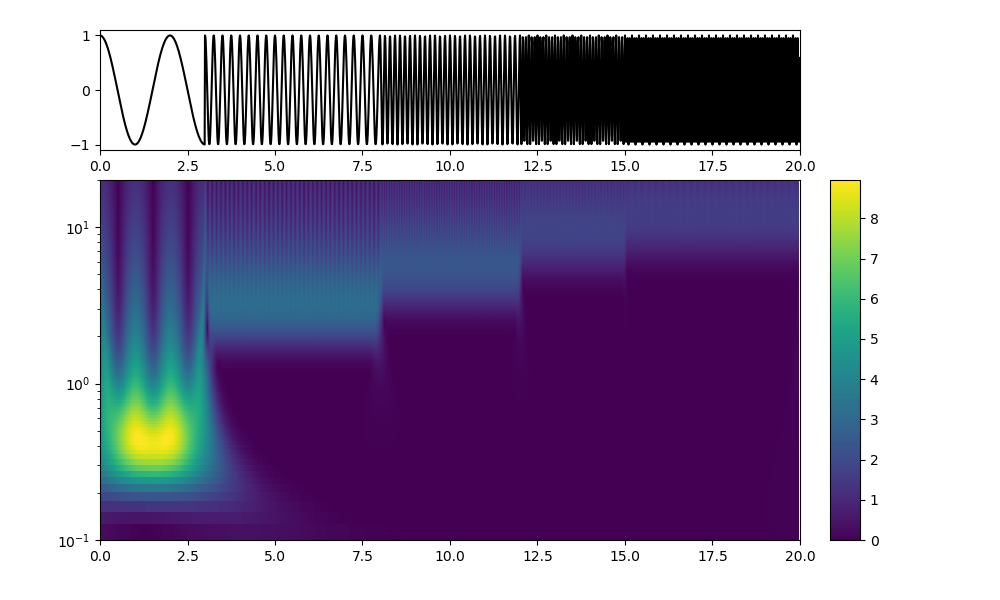
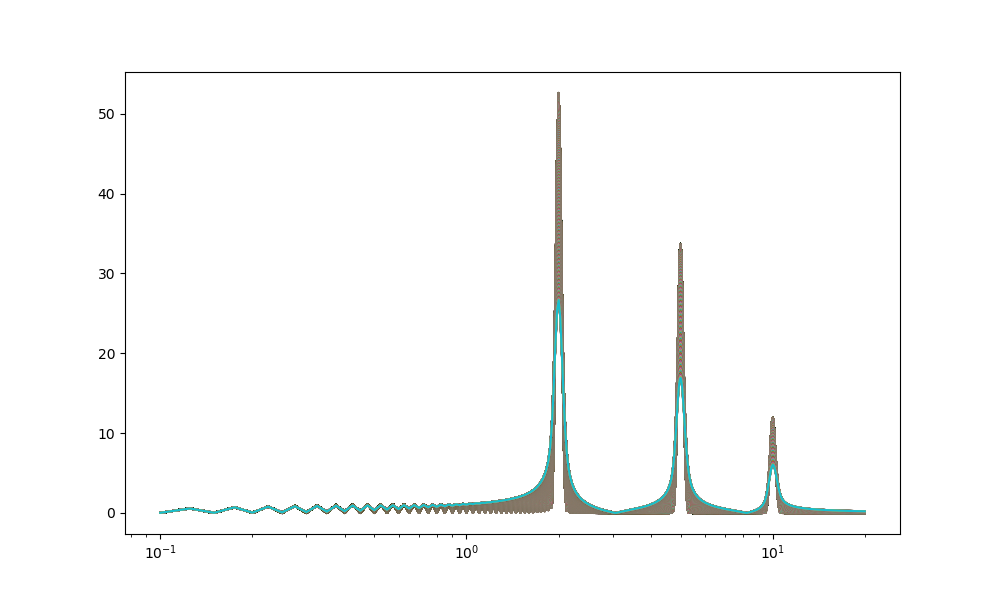
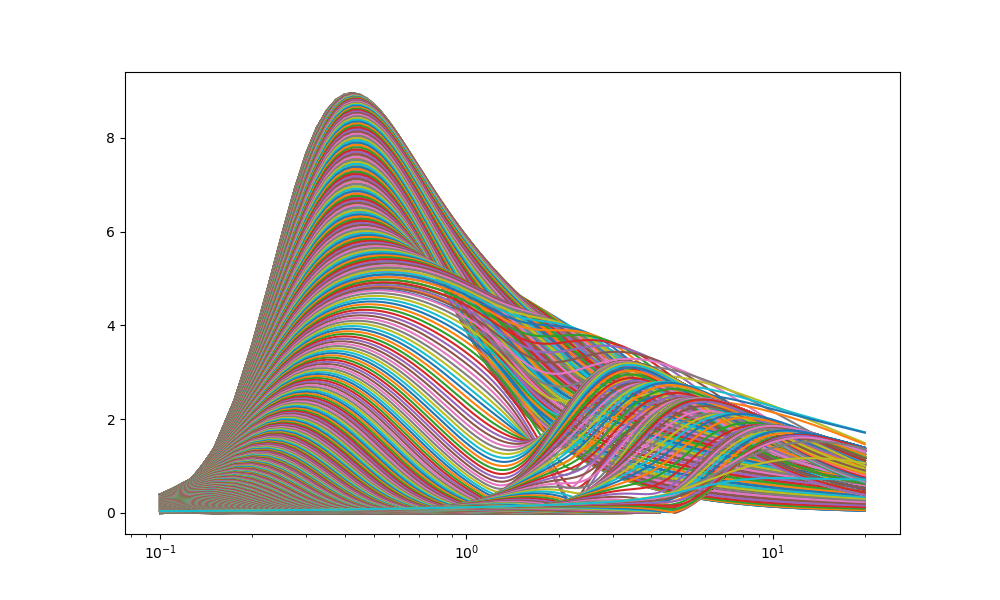
plt.plot(freqs,rr)
plt.xscale('log')
plt.show()
また、小さい周波数で多くの窓関数によるものと思われるゴーストも出現している。
omega0=8;周波数のピークは、一応分離している
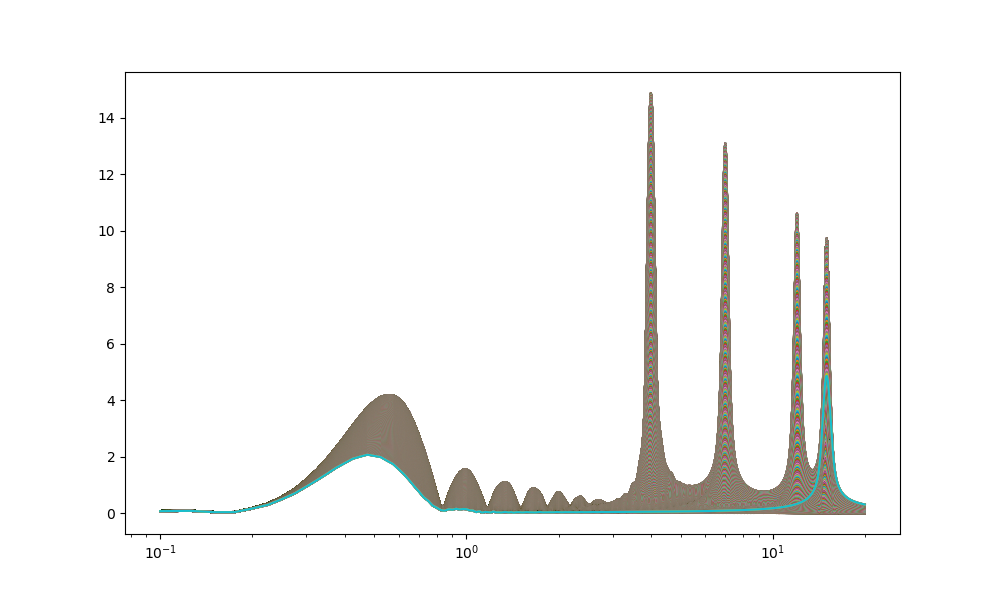
そして以下では、周波数の重なりが大きくなり、より不確定になっている。
omega0=2;高周波領域でオーバーラップが始まった
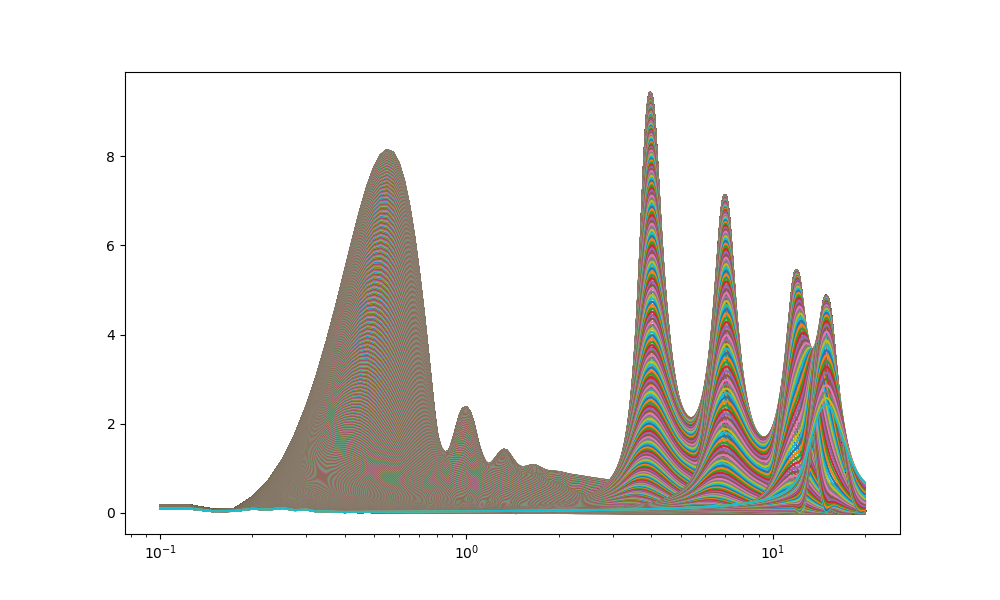
omega0=1;高周波領域でオーバーラップが酷くなった
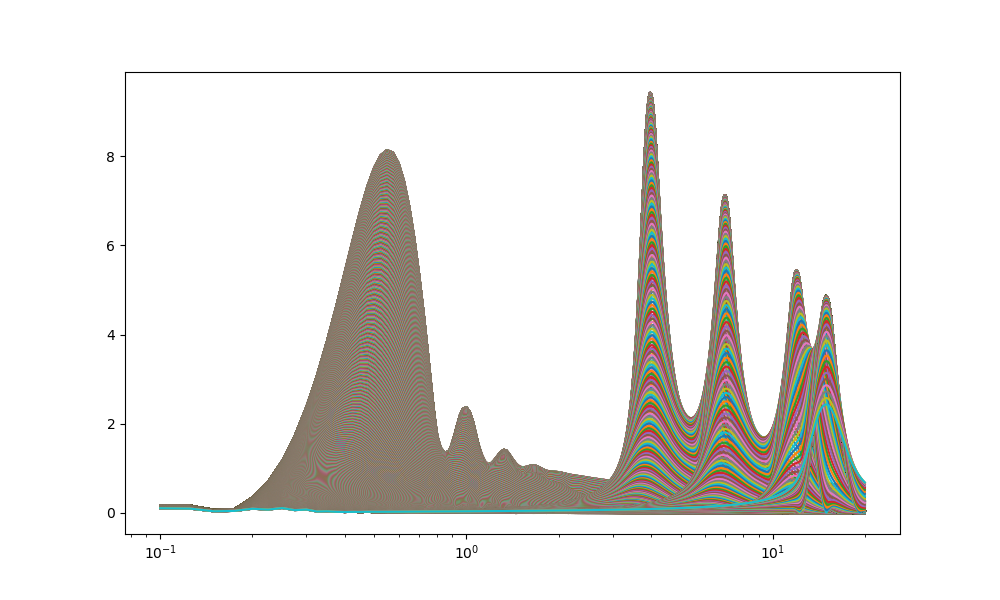
omega0=0.5;かなりオーバーラップしている
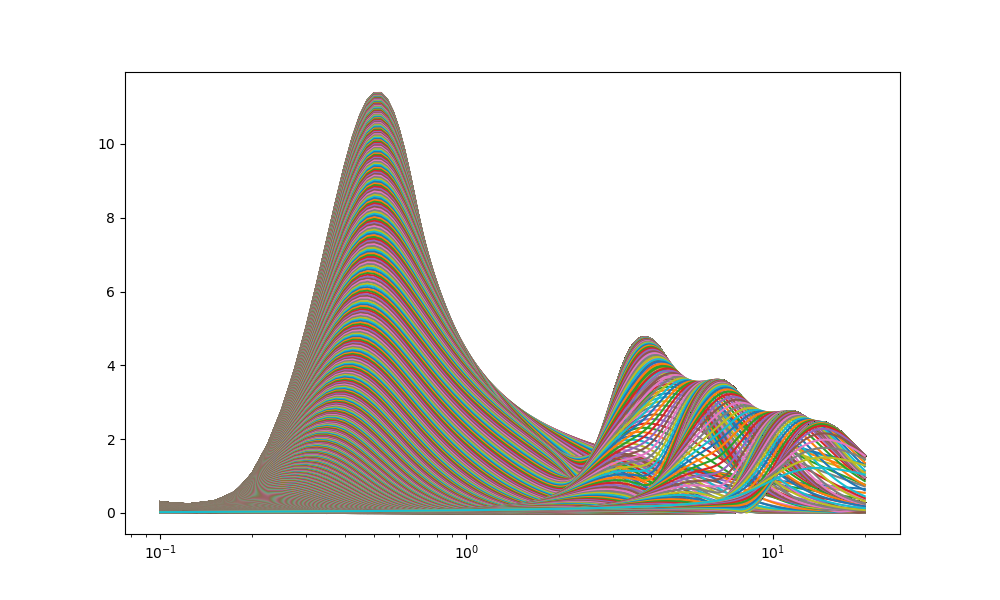
omega0=0.2;ぼけぼけ
まとめ
・FFT、STFT、そしてWavelet変換で起こる不確定性原理について実際に計算しつつ確認した
・FFTでは、共役関係にある時間と周波数依存性は同時には定まらないことが分かる
・STFTとWavelet変換では、どちらもスペクトログラムにおいて不確定性原理が働く現象が現れることが分かった
・次回は、一次元の実時系列データに応用したいと思う
・窓関数は一種の観測窓であり、これはいわゆる観測の理論である
・次々回あたりに、理論的な定式化による裏付けと観測の理論をまとめる予定です
おまけ
実は前回のWavelet変換のScipyサイトの例題の図がもう一つ理解できていなかった。
そこで、今回はSwanのWavelet変換の入力を前回と同じにしてやってみた。
from swan import pycwt
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-1, 1, 0.01)
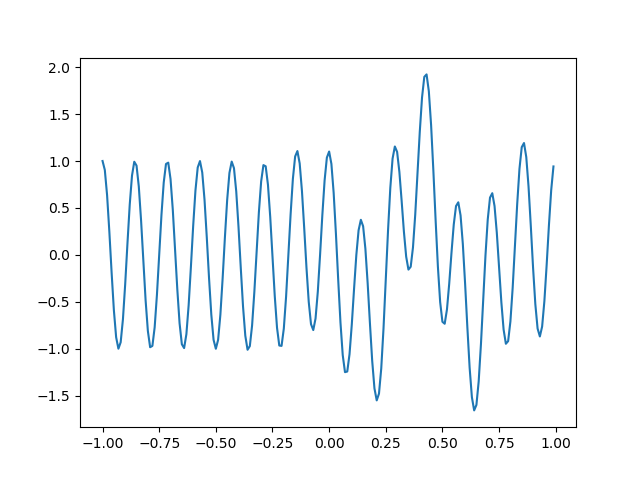
y = np.cos(2 * np.pi * 7 * x) + np.real(np.exp(-7*(x-0.4)**2)*np.exp(1j*2*np.pi*2*(x-0.4))) #change input function
plt.plot(x, y)
plt.show()
Fs = 1/0.01
omega0 = 1
# (1) Freqを指定してcwt
freqs=np.arange(0.1,20,0.025)
r=pycwt.cwt_f(y,freqs,Fs,pycwt.Morlet(omega0))
Z = (r.real, r.imag) #added
rr=np.abs(r) #added
plt.rcParams['figure.figsize'] = (10, 6)
fig = plt.figure()
ax1 = fig.add_axes([0.1, 0.75, 0.7, 0.2])
ax2 = fig.add_axes([0.1, 0.1, 0.7, 0.60], sharex=ax1)
ax3 = fig.add_axes([0.83, 0.1, 0.03, 0.6])
ax1.plot(x, y, 'k')
img = ax2.imshow(np.flipud(rr), extent=[-1, 1,0.1, 20], aspect='auto') #, interpolation='nearest')
twin_ax = ax2
twin_ax.set_yscale('log')
twin_ax.set_xlim(-1, 1)
twin_ax.set_ylim(0.1, 20)
ax2.tick_params(which='both', labelleft=False, left=False)
twin_ax.tick_params(which='both', labelleft=True, left=True, labelright=False)
fig.colorbar(img, cax=ax3)
plt.show()
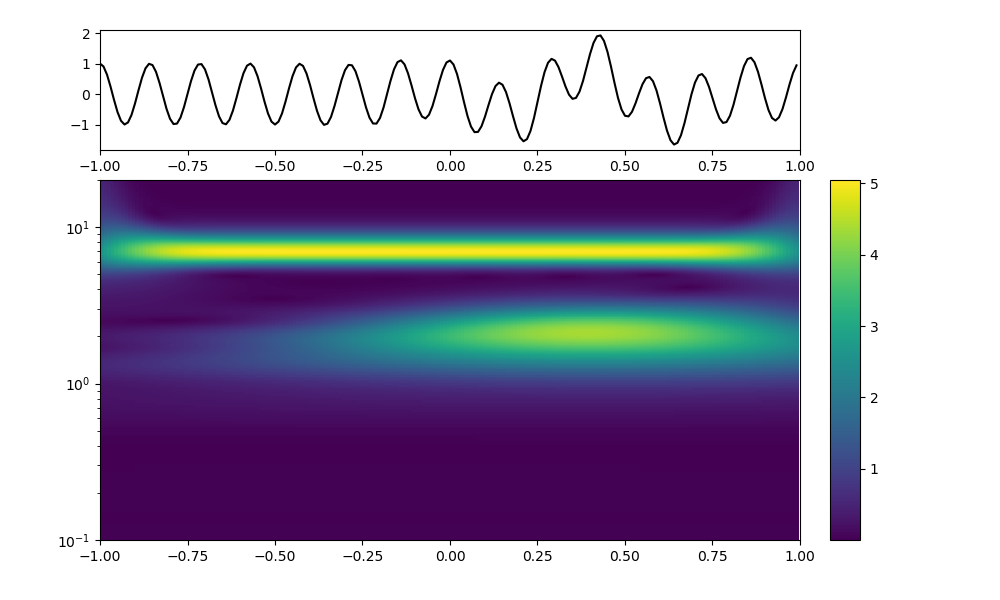
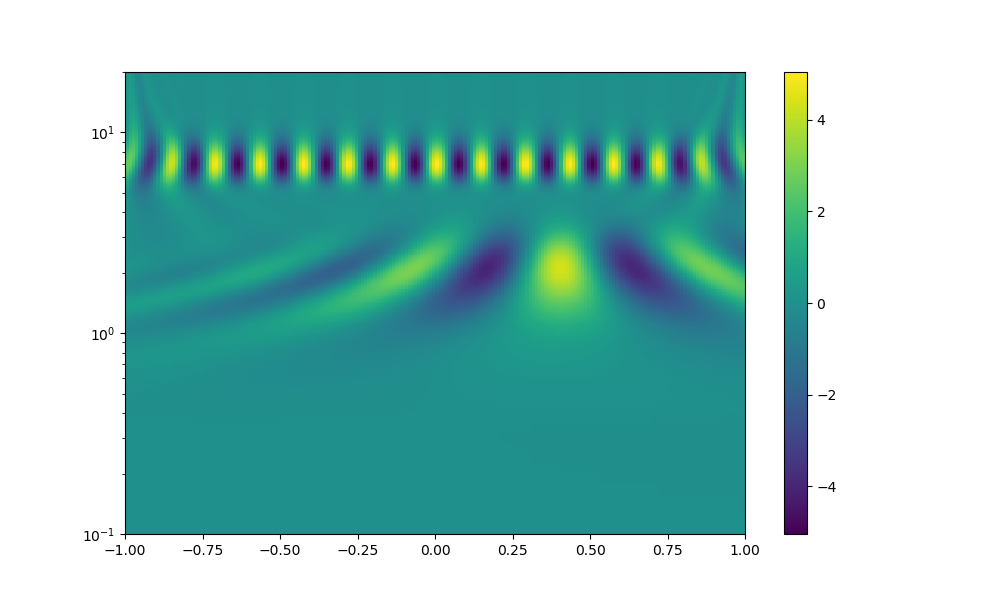
以下を追加して、Scipyのcwtの例題が何を記載しているか確認した。
# added below
fig2=plt.figure()
ax = fig2.add_subplot(111)
img2=ax.imshow(np.flipud(r.real), extent=[-1, 1,0.1, 20], aspect='auto') #, interpolation='nearest')
ax.set_yscale('log')
fig2.colorbar(img2)
plt.show()
以下の通り、振幅(real part of imagenary)を周波数vs時間で記載していることが分かる。
※一応、これですっきりした
⇒ただしScipy使うには、もうちょっとゆっくり考える必要がありそう
plt.plot(freqs,rr)
plt.xscale('log')
plt.show()