こんにちはみなさん
突然pythonで遊び始めて今回で3回目ですが、今回もwavファイルをいじっていきます。
今回はwavで読み出した波形データをフーリエ変換したり、フーリエ逆変換でもとに戻してwavに書き出すことをやっていきます。
Fourier変換
音波
音というのは空気の振動によって発生します(音波)。更にその振動は複数の周波数の振動が重なり合ってできています。
そんな音の振動の中で、支配的な周波数が音の高さを決め、振幅の大きさが音の大きさ、そして、支配的でない様々な周波数の振動が、音の音色を決めています。
Fourier変換
音にはいろんな周波数が含まれているため、そのまま解析するのは大変です。
そこで、音を幾つかの単純な並みの重ね合わせで表そうという方法が発明されました。
これがFourier級数展開です。
f(t) = \sum_k a_k e^{\rm{i}kt}, \ \ \ \ \ e^{\rm{i}kt} = \cos(kt) + \rm{i}\sin(kt)
こんな感じのやつです。
ここでは数学の話はしませんので、わからない場合は、オイラーの公式とかで調べるといいかもです。
さて、ここで$a_k$が分かればこの$f(t)$を近似することができるわけですがこれはどうやって求めると良いのでしょうか。
ちょっとした技巧を使いますが、まず、$f(t)$を特定の時間$T$だけ観察したとします。
先の級数展開の両辺に$e^{-\rm{i}k't}$をかけて、積分してみます。
\int_0^T f(t)e^{-\rm{i}k't}dt = \sum_k a_k \int_0^T e^{\rm ikt - ik't}dt
となります。
ここで$k$を$2n\pi / T$と選んでやると、右辺の積分は$k=k'$のときしか残らなくなりますので、
a_k = \frac{1}{T} \int_0^T f(t)e^{-\rm ikt}dt
この$a_k$を求める計算をFourier変換と呼びます。実際にはこの積分を数値計算によって近似します。
Fourier逆変換
$a_k$が揃うと、Fourier級数展開が完成します。
$a_k$の分布から実空間の関数の形状を生成することをFourier逆変換と呼びます。
wavファイルをFourier変換
とまあ、理論的な話はおいておいて、実際の処理を実施しましょう。
前回同様jupyterを使用します。
まずは例によってwavファイルを読み込みます。
import wave
import struct
from scipy import fromstring, int16
import numpy as np
from pylab import *
%matplotlib inline
wavfile = '/data/input/test.wav'
wr = wave.open(wavfile, "rb")
ch = wr.getnchannels()
width = wr.getsampwidth()
fr = wr.getframerate()
fn = wr.getnframes()
N = 256
span = 15000
print('チャンネル', ch)
print('総フレーム数', fn)
print('サンプル時間', 1.0 * N * span / fr, '秒')
origin = wr.readframes(wr.getnframes())
data = origin[:N * span * ch * width]
wr.close()
print('現配列長', len(origin))
print('サンプル配列長: ', len(data))
これを実行すると、
チャンネル 2
総フレーム数 15884224
サンプル時間 87.07482993197279 秒
現配列長 63536896
サンプル配列長: 15360000
こんな結果になります。
読み出したoriginの配列長がフレーム数の4倍になっているのは、ステレオかつサンプルサイズが2(16bit)なので、1フレームが4バイトになっていることが理由のようですね。
originはバイト文字列なので当然なのでしょうが。。。
とりあえず、取り出したデータをFourier変換しやすいように加工していきましょう。
# ステレオ前提
X = np.frombuffer(data, dtype="int16")
left = X[::2]
right = X[1::2]
まず、サンプルデータをint16で読み込み、左から聞こえてくる音と右から聞こえてくる音に分けます。
次にFourier変換と逆変換(級数展開)を定義しておきます。
今回はnumpyのfftを使用します。
fftはFFT(高速離散フーリエ変換)をするためのライブラリです。
def fourier (x, n, w):
K = []
for i in range(0, w-2):
sample = x[i * n:( i + 1) * n]
partial = np.fft.fft(sample)
K.append(partial)
return K
def inverse_fourier (k):
ret = []
for sample in k:
inv = np.fft.ifft(sample)
ret.extend(inv.real)
print (len(sample))
return ret
関数fourierは各サンプル区間ごとの周波数分布を配列で返してきます。
関数inverse_fourierは周波数分布をもとに、実空間での波形を生成していてます。
今回は特に処理もせず、単純にFourier変換したものを即逆変換して、wavに書き出すだけにしてみます。
Kl = fourier(left, N, span)
Kr = fourier(right, N, span)
freqlist = np.fft.fftfreq(N, d=1/fr)
amp = [np.sqrt(c.real ** 2 + c.imag ** 2) for c in Kl[2500]]
plot(freqlist, amp, marker= 'o', linestyle='-')
axis([0, fr / 2 , 0, 100000])
amp = [np.sqrt(c.real ** 2 + c.imag ** 2) for c in Kr[2500]]
plot(freqlist, amp, marker= 'o', linestyle='-')
まず、Fourier変換してみます。すると、各サンプル区間ごとの周波数分布が得られるので、
適当な瞬間の分布をプロットしてみると、以下のような結果が出ます。
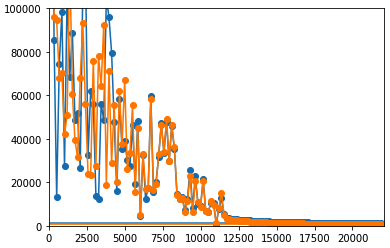
周波数分布がちゃんと出せていることを確認したら、逆変換していきましょう。
def combine_wav (left, right):
ret = []
number = len(right) if len(left) > len(right) else len(left)
for i in range(0, number -1):
data = [int(left[i]), int(right[i])]
ret.extend(data)
return ret
left_dash = inverse_fourier(Kl)
right_dash = inverse_fourier(Kr)
raw_data = combine_wav(left_dash, right_dash)
outd = struct.pack("h" * len(raw_data), *raw_data)
ちょいと面倒くさいですが、ステレオ音源なんで、左音源の逆フーリエと右音源の逆フーリエをミックスさせています。
# 書き出し
outf = '/data/output/test.wav'
ww = wave.open(outf, 'w')
ww.setnchannels(ch)
ww.setsampwidth(width)
ww.setframerate(fr)
ww.writeframes(outd)
ww.close()
で、書き出してみます。
耳音痴の自分でも不自然な感じがしない程度のものができました。
まとめ
wavファイルの内容をFourier変換して遊んでみました。
とりあえず今回はこんなところです。