今夜はなるべく簡単に書こうと思いますが、少し難しいかもしれません。
いわゆる、理論的な話をまとめておこうと思います。
※ただし、使うときに注意点だけ分かれば理論はいらないと思います
とりあえずの目標
以下のとおり、
※リンクされているものは記事にしたものであり、その記事を前提知識として書いて行くので、参照すると理解し易いと思います。
①Scipy環境を作る
・環境の確認
②不確定原理について
・FFT変換・逆変換してみる;時間軸が消える
・STFT変換・逆変換してみる;窓関数について
・wavelet変換・逆変換してみる;スペクトログラムの解釈と不確定原理
③音声や地震データや株価や、。。。とにかく一次元の実時系列データに応用する
音声データ入力編
④FFTからwavelet変換まで簡単にたどってみる(上記以外のちょっと理論)
⑤二次元データに応用してみる
⑥天体観測データに応用してみる
⑦リアルタイムにスペクトログラムしてみる
今回やりたいこと
・FFTに関連してフーリエ変換
・STFTの理論
・Wavelet変換の理論
・FFTに関連してフーリエ変換
【参考】
・フーリエ変換@wikipedia
フーリエ変換
{\hat {f}}(\xi ):=\int _{{-\infty }}^{{\infty }}f(x)\ e^{{-2\pi ix\xi }}\,dx
フーリエ逆変換
{\displaystyle f(x):=\int _{-\infty }^{\infty }{\hat {f}}(\xi )\ e^{2\pi ix\xi }\,d\xi }
以下、Wikipediaより引用を「」で示す。
「対象の関数における独立変数が物理量の場合、フーリエ変換は独立変数の次元をもとの逆数に移す。例えば、変換前の関数における独立変数 x が時間の次元をもつとき、変換後の独立変数 ξ は周波数の次元を持つ。あるいは、変換前の独立変数 x が長さの次元をもつとき、変換後の独立変数 ξ は波数の次元を持つ。この性質は定義より x ξ が無次元量であることから従う。」
さらに、不確定性原理について
「一般的に言って、$f(x)$ が凝縮されればされるほどそのフーリエ変換 ${\hat {f}}$はより拡散される。特に、フーリエ変換のスケール性からわかることとして、函数を $x$ において「圧搾」するならば、そのフーリエ変換は $ξ$ において「伸展」される。したがって、函数とそのフーリエ変換の両方ともを勝手に凝縮させることはできない。」
「$x = 0$ の周りでの拡散は以下の式で定義される
※「0 の周りでの分散」(dispersion about zero) によって測ることができる」
D_{0}(f)=\int _{{-\infty }}^{\infty }x^{2}|f(x)|^{2}\,dx
「このとき不確定性原理は、函数 $ƒ(x)$ が絶対連続で、函数 $x·ƒ(x)$ および $ƒ′(x)$ が自乗可積分であるならば
{\displaystyle D_{0}(f)D_{0}({\hat {f}})\geq {\frac {1}{16\pi ^{2}}}} D_{0}(f)D_{0}({\hat {f}})\geq {\frac {1}{16\pi ^{2}}}
が成り立つことを述べる」
そして、これは
「量子力学において、運動量と位置の波動函数は(プランク定数を因子に持つ)フーリエ変換対である。プランク定数を厳密に勘定に入れることで、上述の不等式はハイゼンベルクの不確定性原理を記述する[2]。」
ということで、根っこのところでは、フーリエ変換の不確定性原理と量子力学の不確定性原理は共役量の間で成り立つ普遍的な原理である。
・STFTの理論
【参考】
・短時間フーリエ変換
「短時間フーリエ変換(STFT)とは、関数に窓関数をずらしながら掛けて、それにフーリエ変換すること。」
「STFTは以下のように数式表現できる(iは虚数単位):
{\mathrm {STFT}}_{{x,w}}(t,\omega )=\int _{{-\infty }}^{{\infty }}x(\tau )w(\tau -t)e^{{-i\omega \tau }}\,d\tau
ここで${\displaystyle w(t),}$は窓関数であり、普通 $t=0,$付近に中心をもつ山の概形をしていて、$t=0,$の付近から離れると 0 になる関数である。」
※つまり、時刻$t$だけ窓関数をずらしてフーリエ変換して、STFTを$(t,\omega)$面内で求めていくことを意味する。
「STFTの絶対値を2乗することで、パワースペクトルの時間変化が得られる:
{\mathrm {power}}_{{x,w}}(t,\omega )=|{\mathrm {STFT}}_{{x,w}}(t,\omega )|^{2}\,
また、位相スペクトルの時間変化は、STFTの偏角で得られる:
{\mathrm {phase}}_{{x,w}}(t,\omega )=\arg {\mathrm {STFT}}_{{x,w}}(t,\omega )
「不確定性原理(フーリエ変換の不確定性原理)とは、時刻の不確定さと周波数の不確定さの間に
\Delta x\Delta \omega \geq {\frac {1}{2}}
の関係があることである。一般化された言い方では、フーリエ変換で結ばれた2つの変数の対に対して上のような関係がなりたつことを指す。」
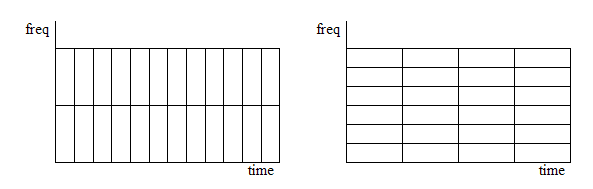
「STFTの解像度の比較。左は時間分解能が良く、右は周波数分解能が良い」
「この事実はウェーブレット変換を作る原因にもなった。ウェーブレット変換ではSTFTと異なり時間分解能と周波数分解能が両立する(独立に変更する)ことが出来る。」
※()は補った、
※またfreq,timeは共役量でありwavelet変換に置いても不確定性原理は発生することに注意
・Wavelet変換の理論
【参考】
・ウェーブレット変換@wikipedia
「ウェーブレットは以下の許容条件を満たす。即ち、 ${\hat {\psi }}$を $\psi$ のフーリエ変換として、
C_{{\psi }}=2\pi \int d\xi \left|\xi \right|^{{-1}}\left|{\hat {\psi }}(\xi )\right|^{{2}}<\infty
もし $\psi \in L^{{1}}({\mathbf {R}})$ならば、そのフーリエ変換 ${\hat {\psi }}$は連続であり、上の許容条件は ${\hat {\psi }}(0)=0$つまり $\int dx, \psi (x)=0 $の時にのみ満たされる。 この許容条件を満たすウェーブレットに対しウェーブレット変換が以下の様に定義される。
(T^{\text{wav}}f)(a,b):=\int dx\left|a\right|^{-1/2}f(x){\overline {\psi \left({\frac {x-b}{a}}\right)}}
ここで、 $a$はscale、 $b$はtranslationを表す。$\psi (x)$を、マザーウェーブレットと言う。
※【補足】STFTと比較すると$b$だけでなく$a$も独立に変更できるところがミソである。
元の関数は、以下の式で得られる。
f(x)=C_{\psi }^{-1}\int _{-\infty }^{\infty }da\int _{-\infty }^{\infty }db~a^{-2}(T^{\text{wav}}f)(a,b)\psi \left({\frac {x-b}{a}}\right)
例えばウェーブレットにはメキシカンハット関数 $\psi (t)=(1-t^{{2}})\exp(-t^{2}/2)$や、 変形ガウシアン $\psi (x)=\pi ^{{-1/4}}(e^{{-ix\pi (2/\ln 2)^{{1/2}}}}-e^{{-ix\pi ^{{2}}(2/\ln 2)}})e^{{-x^{{2}}/2}}$などがある。」
「連続ウェーブレット変換は、FFT(高速フーリエ変換)を用いて計算できる。数値計算で連続ウェーブレット変換を求める場合、スケールパラメータ $a$ を変化させながら、マザーウェーブレット $\psi (x)$ と信号 $f(x)$ のフーリエ変換を計算し、畳み込みを計算した後、逆フーリエ変換によって時間領域に戻す事で連続ウェーブレット変換を求める事が出来る。」
※当然の帰結としてwavelet変換においても、不確定性原理は成り立っている。
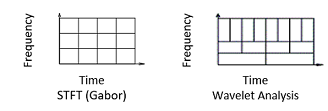
そして、STFTとの大きな違いは、分解能が悪くなりがちな低周波数領域においてもスケール$a$を適度に変更することにより、一定の分解能を得られる可能性があることである。
【参考】
・連続ウェーブレット変換およびスケールベースの解析@Mathworks
まとめ
・フーリエ変換、STFT、そしてwavelet変換の理論をおさらいした
・共役量の間には普遍的に成り立つ不確定性原理が存在する
・STFTとwavelet変換の違いが理解できた
・スペクトログラム(スカログラム@wavelet変換)や位相スペクトラムをさらに発展的に有効利用しよう
おまけ
【参考】
・信号アナライザーでのスカログラム計算@Mathworks
「スカログラムは信号の連続ウェーブレット変換 (CWT) の絶対値で、時間と周波数の関数としてプロットされます。スカログラムは、低周波数成分を含む信号や、周波数成分が急激に変化する信号を識別する場合、スペクトログラムより便利な場合があります。短時間の高周波数イベントにおける時間の位置推定と長時間の低周波数イベントにおける周波数の位置推定を向上させたい場合に、スカログラムを使用します。
入力信号を無限時間の正弦波に分解するスペクトログラムとは異なり、CWT は "ウェーブレット" に信号を分解します。ウェーブレットは、周波数と時間の両方で位置決めされるため、突然の変化による中断を伴う規則的な振る舞いを示すデータの解析に優れています。つまり、ウェーブレットには開始と終了があります。ウェーブレットが有限であるため、振幅と形状を制御するだけでなく、位置も制御することができます。この追加の自由度により、CWT では、過渡状態を検出し、信号の周波数が急激に変化している領域を特定できます。」