第三夜は、方策ネットワークについて記述します。
ある意味考え方として前半の最大の山場です。
基本的には、昨夜のChainerの基本がもとになります。
説明したいこと
（１）基本はMNISTと同じ
（２）入力チャンネルについて
（３）出力チャンネルについて
（４）方策ネットワークのコード
（１）基本はMNISTと同じ
ということで、mnistのモデルをおさらいしましょう。
ネットワーク定義は以下のとおりでした。
# ネットワーク定義
class MLP(Chain):
def __init__(self, n_units):
super(MLP, self).__init__()
with self.init_scope():
self.l1 = L.Linear(None, n_units) # 入力層
self.l2 = L.Linear(None, n_units) # 中間層
self.l3 = L.Linear(None, 10) # 出力層
def __call__(self, x):
h1 = F.relu(self.l1(x))
h2 = F.relu(self.l2(h1))
return self.l3(h2)
MNISTの場合の入力はｘであり、以下のようなものである。
x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
つまり、（NONE,28,28,1）です。ここで最後の１がいわゆるチャンネルと呼ばれるものです。すなわちMNISTのデータは以下のような28×28のサイズで白黒の画像でした。
※実際の10倍のサイズで描いています
カラー画像では、同じ大きさであれば(NONE,28,28,3)なります。
※実際の10倍のサイズで描いています
一方、出力はMNISTの場合は、0～9までの値になります。
つまり出力は１次元で10チャンネルです。
したがって、MNISTでは入力が(NONE,28,28,1)で出力は(NONE,10)になります。
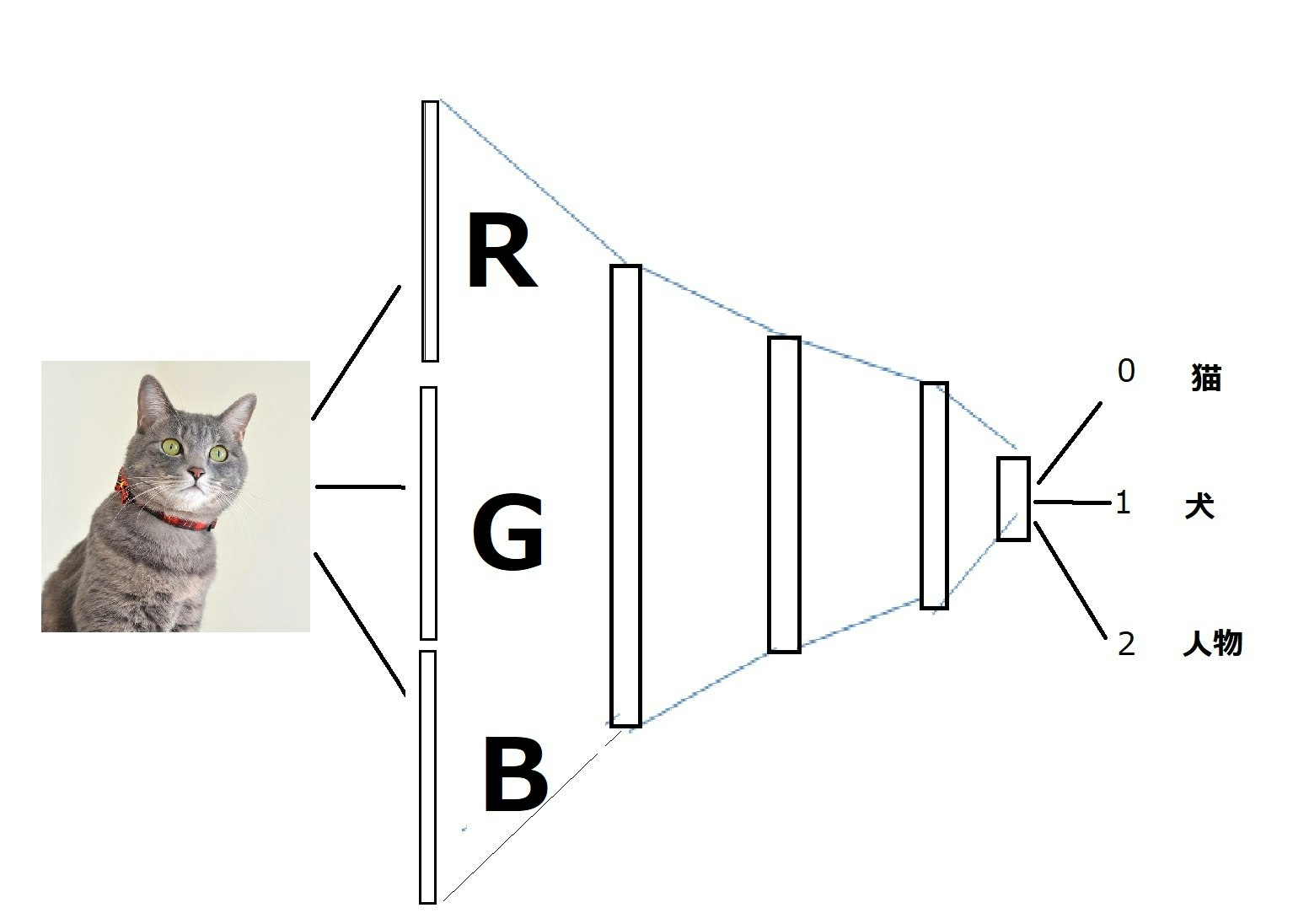
例えば、サイズ（28，28）のカラー画像の犬、猫、人を入力として、分類する場合は出力は３（犬、猫、人）個になります。
つまり、入力（NONE,28,28,3）に対して出力は(NONE,3)になります。
図で描くと以下のようになります。
「それでは、将棋の場合の入力と出力はどうなるでしょう。」
というのが次に問題になります。
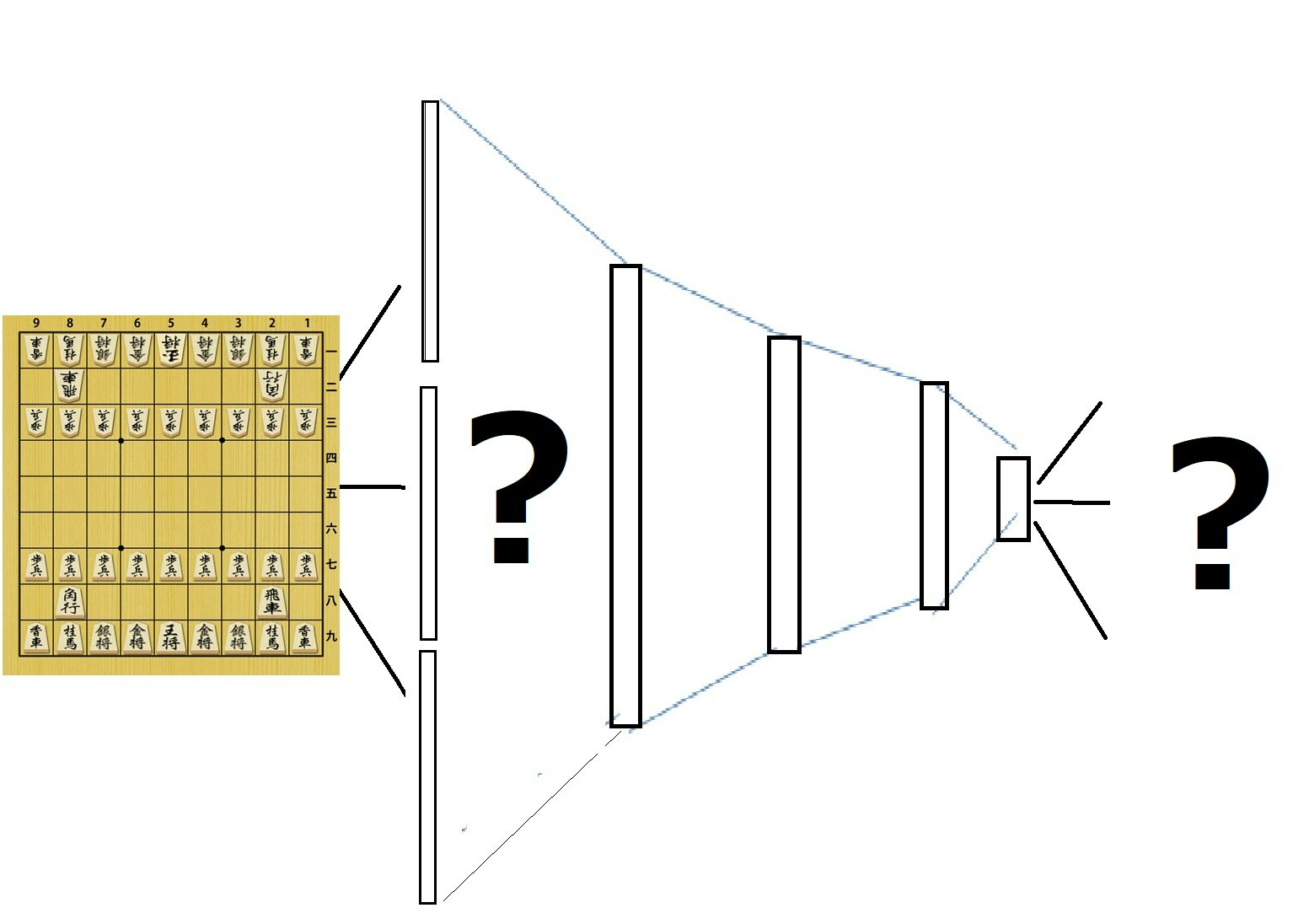
（２）入力チャンネルについて
まず、サイズについては、とりあえず9×9でいいでしょう。
そして、入力チャンネルは。。。これが本書で解説されています。
つまり、独立な駒の数です。
すなわち駒の数だけ盤つまりR,G,Bに対応するチャンネルを用意します。
独立な駒の数は全部で１０４個です。
内訳は、
（先手、後手の２）×（盤面上の駒数（普通の駒８＋成り駒６）＋持ち駒になりうる駒の数（歩１８、香車４、桂馬４、銀４、金４、角２、飛車２））
だそうです。
そして、それぞれの駒は盤面上に存在すれば１、存在しないマスでは０を入れると約束とします。
こうすることにより、これらのチャンネルのすべてを重ね合わせれば、瞬間瞬間の盤面の様子を再現できます。
これで、入力は猫の分類と大して変わらないというのが分かると思います。
すなわち、入力データは（NONE,9,9,104）になります。
（３）出力チャンネルについて
出力チャンネルとは将棋においては、次の一手を盤面でどこに何を打つかということです。
ここで一つの発明が記載されています。
つまり、盤上の駒が移動する場合、すべての組み合わせで移動を表現すると移動元と移動先の場合分けから８１×８１＝６５６１通りとなります。
しかし、実際の将棋の場合は、移動元は移動先から見てどこから移動してきたかが分かれば、一意に決まるということです。それは将棋では駒を飛び越えて移動することがないためであるとのことです。
※確かにそうです
ということで、盤面上の駒ではその移動元の方向が４（左右前後方向）＋４（斜め４方向）＋２（桂馬の移動）＝１０です。
一方、持ち駒は７種類あるので７、成るのも移動元移動先の考え方で１０通りとなります。ということでラベルとして２７通りを割り当て、これが８１マスに対して存在するので、全体の出力ラベル数は２７×８１＝２１８７通りとなります。
これが将棋の次の一手としてのラベル、すなわちMNISTなら１０だったし、猫の分類なら３だったものになります。
つまり、実際のコードではもう一工夫されていますが、とりあえず出力データは（NONE,2187）となります。
（４）方策ネットワークのコード
実際、本書では以下のコードが示されています。
ch = 192
class PolicyNetwork(Chain):
def __init__(self):
super(PolicyNetwork, self).__init__()
with self.init_scope():
self.l1=L.Convolution2D(in_channels = 104, out_channels = ch, ksize = 3, pad = 1)
self.l2=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l3=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l4=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l5=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l6=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l7=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l8=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l9=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l10=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l11=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l12=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
self.l13=L.Convolution2D(in_channels = ch, out_channels = MOVE_DIRECTION_LABEL_NUM, ksize = 1, nobias = True)
self.l13_bias=L.Bias(shape=(9*9*MOVE_DIRECTION_LABEL_NUM))
def __call__(self, x):
h1 = F.relu(self.l1(x))
h2 = F.relu(self.l2(h1))
h3 = F.relu(self.l3(h2))
h4 = F.relu(self.l4(h3))
h5 = F.relu(self.l5(h4))
h6 = F.relu(self.l6(h5))
h7 = F.relu(self.l7(h6))
h8 = F.relu(self.l8(h7))
h9 = F.relu(self.l9(h8))
h10 = F.relu(self.l10(h9))
h11 = F.relu(self.l11(h10))
h12 = F.relu(self.l12(h11))
h13 = self.l13(h12)
return self.l13_bias(F.reshape(h13, (-1, 9*9*MOVE_DIRECTION_LABEL_NUM)))
このコードは、上記のMNISTのコードと中間層の厚さとL.Convolution2Dと２次元の処理をしているところは異なりますが、ほとんど同じです。
ch = 192
class PolicyNetwork(Chain):
def __init__(self):
super(PolicyNetwork, self).__init__()
with self.init_scope():
self.l1=L.Convolution2D(in_channels = 104, out_channels = ch, ksize = 3, pad = 1)
は
# ネットワーク定義
class MLP(Chain):
def __init__(self, n_units):
super(MLP, self).__init__()
with self.init_scope():
self.l1 = L.Linear(None, n_units) # 入力層
と若干異なりますが、よく対応しています。
また、
def __call__(self, x):
h1 = F.relu(self.l1(x))
def __call__(self, x):
h1 = F.relu(self.l1(x))
この部分は層数が異なりますが、全く同じです。
そして最後の部分、
h13 = self.l13(h12)
return self.l13_bias(F.reshape(h13, (-1, 9*9*MOVE_DIRECTION_LABEL_NUM)))
と
h2 = F.relu(self.l2(h1))
return self.l3(h2)
は少し異なっているように見えますが、方策ネットワークをよく見ると
self.l13=L.Convolution2D(in_channels = ch, out_channels = MOVE_DIRECTION_LABEL_NUM, ksize = 1, nobias = True)
self.l13_bias=L.Bias(shape=(9*9*MOVE_DIRECTION_LABEL_NUM))
となっているので、ここで辻褄があっているようです。そしてこの
self.l13_bias=L.Bias(shape=(9*9*MOVE_DIRECTION_LABEL_NUM))が一工夫で、チャンネルにたいしてバイアスという重みを個別に加えています。
また、中間層が方策ネットワークでは
self.l2=L.Convolution2D(in_channels = ch, out_channels = ch, ksize = 3, pad = 1)
と二次元のネットワークを利用しているためです。
ここでksize=3は3×3のフィルターサイズです。またpad=1として、中間層のサイズの辻褄を合わせています。
ちなみにOutputWidth, OutputHeight, Pad, FilterWidth, FilterHeight, InputWidth, InputHeightから以下のように導出できます。
OW=IW + 2P ‐ FW + 1
OH=IH + 2P - FH + 1
また、最後のksize = 1は1×1のフィルターで、GoogleがAlphaGoで利用した、このフィルターによる畳み込みは全結合に比べてパラメータを削減できるということです。
まとめ
・方策ネットワークの考え方をMNISTのネットワーク定義と対比しつつ解説した
・将棋AIの入力チャンネルと出力チャネルの意味と導出を解説した
・方策ネットワークのコードをMNISTのネットワークのコードと対比して類似性を見た
・次回は実際に動く様子を見たいと思う
・実際には、MLPのコードでは、self.l1 = L.Linear(None, n_units)を使っており、L.Convolution2Dとはことなる。
L.Convolution2Dの入力だと、L.Linearの入力から変更して、(NONE,28,28,1)のような４次元で与える必要がある。
例としては、前回のKerasMnistのコードを見ればイメージできると思う。さらにChainerだと以下のような参考を読むとConvolution2DでMNISTコードを記載できるだろうが、今回はそこまで踏み込めなかった。
【参考】
・Chainer の MNIST サンプルを試す
また、Cifar10というカラー画像の識別には以下のようにVGGというモデルを利用しており、それはConvolution2Dで構成されている。
・chainer/examples/cifar/models/VGG.py