【SEIRモデル入門】COVID-19データをフィッティングしてみる♬

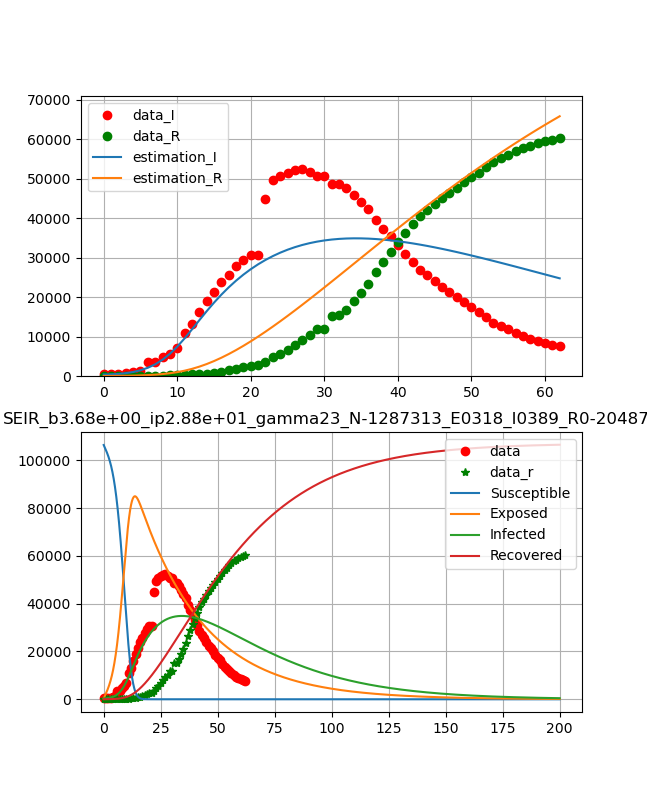
新型コロナの感染データをSEIRモデルを用いて、フィッティングしてみた。
手法は前回の【minimize入門】SEIRモデルでデータ解析する♬と同様である。感染データは以下の参考サイトから入手した。
武漢のデータに対して【matplotlib入門】COVID-19データから終息時期を読む♬において、以下の結果を得た。

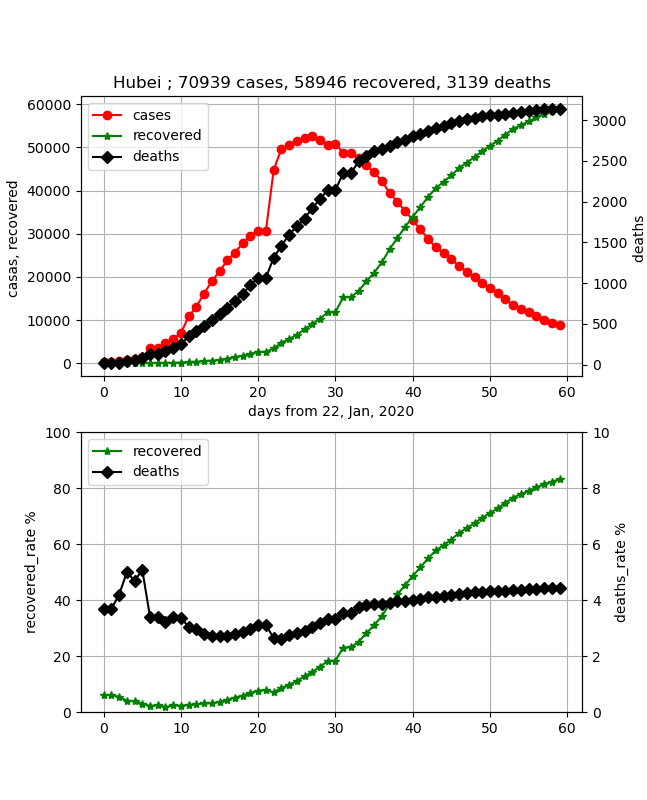
これをそれらしい曲線が得られるように初期値を選んでフィッティングしたものが以下のように得られる。

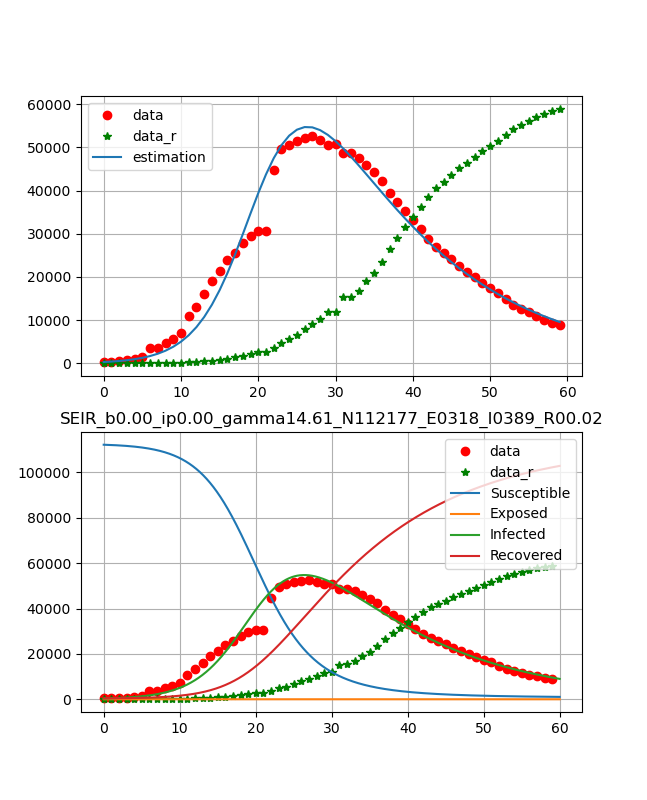
ということで、今回は各国について同様なフィッティングを行って、新たな知見が得られるか検討したいと思う。なお、データは以下から入手しており、断らない限りは2020年3月24日時点のデータであるが、上記は2020年3月22日時点のものである。また、コード解説で説明するが、今回はフィッティングは感染データに対してのものと、治癒データも利用したフィッティングを別のプログラムで実行しているので、注意してください。
【参考】
CSSEGISandData/COVID-19

やったこと

・日本の終息
・コード説明
・各国データのフィッティング

・日本の終息

上記のように穏やかに書こうと思ったが、東京都が都市封鎖と言い出したので、先に日本の終息は見えるのかというのを記載したいと思う。
結論から言うと、あとひと月見れば終息が確実に見えそうという状況である。
実は、上記の3月22日のデータでは、ちょっと寝てきてこれが感染ピークならという状況もあったが、ここで少し感染数が直線的に伸びてきたので、飽和は少し先伸ばしになった。
ということで、フィッティングとしては3月24日までのデータに対して以下のグラフを得た。

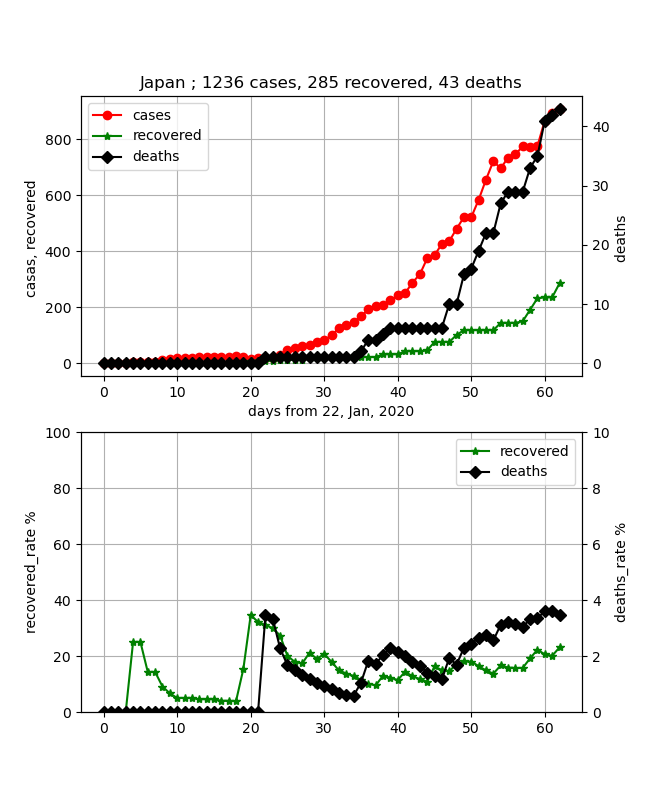
フィッティングは感染数と治癒の両方の曲線を同時に決定している。
日本のデータは53日－59日のデータが少しおかしいが概ね自然に推移している。
ということで、以下のように綺麗な曲線が得られた。
つまり、10日程でピークが表れ、ひと月ほどで治癒曲線がピークとなり、あとはなだらかに終息していくという結果である。

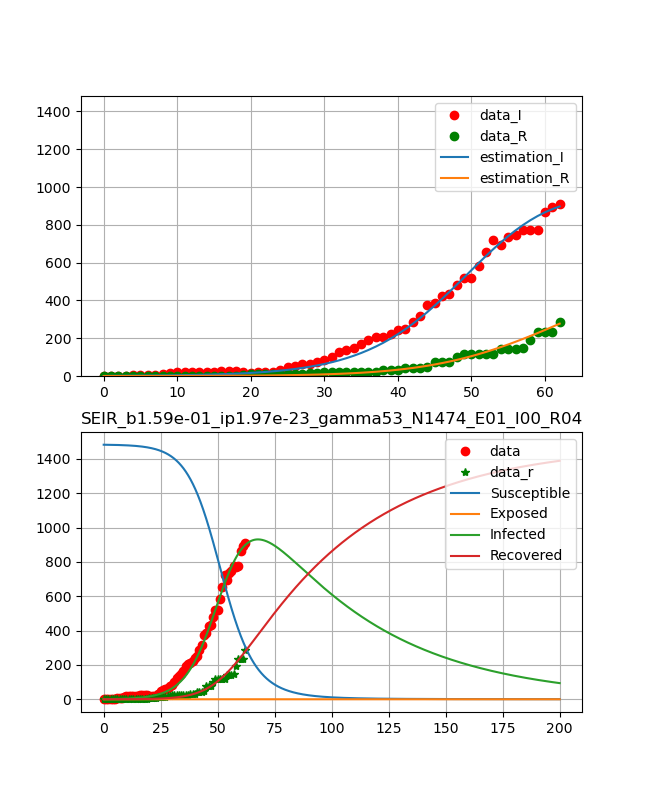
得られたパラメータは、

beta_const=0.159
lp=1.97e-23
gamma=52.7
N=1474
R0 = 4.45

・コード説明

コード全体は以下においた。
二つ置いた理由は、提供されているデータ構造が変わって現在のデータでは②のように個別に読む必要がある。また、②では曲線によりフィットしやすいように、フィッティング関数を通常の最尤関数から普通の二乗誤差に変更した。
①collective_particles/fitting_COVID.py
②collective_particles/fitting_COVID2.py

以下、簡単なコードを解説する。
以下のLibを利用する。
前２回の記事のものを合算したものとなっている。

#include package
import numpy as np
from scipy.integrate import odeint
from scipy.optimize import minimize
import matplotlib.pyplot as plt
import pandas as pd

以下も感染データ描画と同様である。

#pandasでCSVデータ読む。
data = pd.read_csv('COVID-19/csse_covid_19_data/csse_covid_19_time_series/time_series_19-covid-Confirmed.csv')
data_r = pd.read_csv('COVID-19/csse_covid_19_data/csse_covid_19_time_series/time_series_19-covid-Recovered.csv')
data_d = pd.read_csv('COVID-19/csse_covid_19_data/csse_covid_19_time_series/time_series_19-covid-Deaths.csv')

confirmed = [0] * (len(data.columns) - 4)
confirmed_r = [0] * (len(data_r.columns) - 4)
confirmed_d = [0] * (len(data_d.columns) - 4)
days_from_22_Jan_20 = np.arange(0, len(data.columns) - 4, 1)

#City
city = "Hubei" #武漢のデータ

#データを加工する
t_cases = 0

for i in range(0, len(data), 1):
    #if (data.iloc[i][1] == city): #for country/region
    if (data.iloc[i][0] == city):  #for province:/state  
        print(str(data.iloc[i][0]) + " of " + data.iloc[i][1])
        for day in range(4, len(data.columns), 1):
            confirmed[day - 4] += data.iloc[i][day] -  data_r.iloc[i][day] 
            confirmed_r[day - 4] += data_r.iloc[i][day]
            confirmed_d[day - 4] += data_d.iloc[i][day]

SEIRモデルを使う。

#define differencial equation of seir model
def seir_eq(v,t,beta,lp,ip,N0):
    N=N0 #int(26749*1) #58403*4
    a = -beta*v[0]*v[2]/N
    b = beta*v[0]*v[2]/N-(1/lp)*v[1] #N
    c = (1/lp)*v[1]-(1/ip)*v[2]
    d = (1/ip)*v[2]
    return [a,b,c,d]

ここでN0の値によって得られる絵が変わってくる。
これをフィッティングするのもいいが今回はできていない。
Hubeiのフィッティングに際しては、以下の値を参考にさせていただいた。
ただし、NおよびS0に関してはゲームの参加者という意味で住人が全員ではなく感染する対象と考え方でほぼ実際の感染者数（の周りで動かした値）を採用した。
【参考】
・SEIRモデルで新型コロナウイルスの挙動を予測してみた。
初期値等設定

#solve seir model
N0 = 70939 #Hubei
N,S0,E0,I0=int(N0*1.),N0,int(318),int(389) #N is total population, S0 initial value of fresh peaple
ini_state=[S0,E0,I0,0] #initial value of diff. eq.
beta,lp,ip=1, 2, 7.4 
t_max=60 #len(days_from_22_Jan_20)
dt=0.01
t=np.arange(0,t_max,dt)
obs_i = confirmed

入力パラメータに対して、評価値を返す関数。以下はv[2]；感染数を返している。

#function which estimate i from seir model func 
def estimate_i(ini_state,beta,lp,ip,N):
    v=odeint(seir_eq,ini_state,t,args=(beta,lp,ip,N))
    est=v[0:int(t_max/dt):int(1/dt)]
    return est[:,2]

以下最小化の目的関数（以下は最尤関数を利用）。

#define logscale likelihood function
def y(params):
    est_i=estimate_i(ini_state,params[0],params[1],params[2],params[3])
    return np.sum(est_i-obs_i*np.log(np.abs(est_i)))

minimize@scipyで最小値を求め、基本再生産数を計算。

#optimize logscale likelihood function
mnmz=minimize(y,[beta,lp,ip,N],method="nelder-mead")
print(mnmz)
#R0
beta_const,lp,gamma_const,N = mnmz.x[0],mnmz.x[1],mnmz.x[2],mnmz.x[3] #感染率、感染待時間、除去率（回復率）
print(beta_const,lp,gamma_const,N)
R0 = N*beta_const*(1/gamma_const)
print(R0)

計算結果をグラフ表示。

#plot reult with observed data
fig, (ax1,ax2) = plt.subplots(2,1,figsize=(1.6180 * 4, 4*2))
lns1=ax1.plot(obs_i,"o", color="red",label = "data")
lns2=ax1.plot(confirmed_r,"*", color="green",label = "data_r")
lns3=ax1.plot(estimate_i(ini_state,mnmz.x[0],mnmz.x[1],mnmz.x[2],mnmz.x[3]), label = "estimation")
lns0=ax1.plot(t,odeint(seir_eq,ini_state,t,args=(mnmz.x[0],mnmz.x[1],mnmz.x[2],mnmz.x[3])))
lns_ax1 = lns1+lns2 + lns3 + lns0
labs_ax1 = [l.get_label() for l in lns_ax1]
ax1.legend(lns_ax1, labs_ax1, loc=0)
ax1.set_ylim(0,N0)

以下は終息が見えるように、ロングスパンのグラフを表示する。
※ここでは200日まで表示
これにより、最初に示した武漢のような結果が得られる。
ただし、武漢の絵は60日までの絵である。

t_max=200 #len(days_from_22_Jan_20)
t=np.arange(0,t_max,dt)

lns4=ax2.plot(obs_i,"o", color="red",label = "data")
lns5=ax2.plot(confirmed_r,"*", color="green",label = "recovered")
lns6=ax2.plot(t,odeint(seir_eq,ini_state,t,args=(mnmz.x[0],mnmz.x[1],mnmz.x[2],mnmz.x[3])))
ax2.legend(['data','data_r','Susceptible','Exposed','Infected','Recovered'], loc=1)
ax2.set_title('SEIR_b{:.2f}_ip{:.2f}_gamma{:.2f}_N{:.2f}_E0{:d}_I0{:d}_R0{:.2f}'.format(beta_const,lp,gamma_const,N,E0,I0,R0))
ax1.grid()
ax2.grid()
plt.savefig('./fig/SEIR_{}_b{:.2f}_ip{:.2f}_gamma{:.2f}_N{:.2f}_E0{:d}_I0{:d}_R0{:.2f}_.png'.format(city,beta_const,lp,gamma_const,N,E0,I0,R0)) 
plt.show()
plt.close()

一方、感染数と治癒数の同時フィッティングでは途中の評価関数と目的関数を以下のように変更した。

#function which estimate i from seir model func 
def estimate_i(ini_state,beta,lp,ip,N):
    v=odeint(seir_eq,ini_state,t,args=(beta,lp,ip,N))
    est=v[0:int(t_max/dt):int(1/dt)] 
    return est[:,2],est[:,3] #v0-S,v1-E,v2-I,v3-R

#define logscale likelihood function
def y(params):
    est_i_2,est_i_3=estimate_i(ini_state,params[0],params[1],params[2],params[3])
    return np.sum((est_i_2-obs_i_2)*(est_i_2-obs_i_2)+(est_i_3-obs_i_3)*(est_i_3-obs_i_3))

なお、この場合は感染数のみや治癒数のみのフィッティングも可能である。

・各国データのフィッティング

・イラン
治雄率が比較的大きいイランは日本よりより早く飽和し、終息に向かいそうであるが、まだまだ感染数が伸びており、治癒率も伸び悩んでいるので、もっとかかる可能性もある。

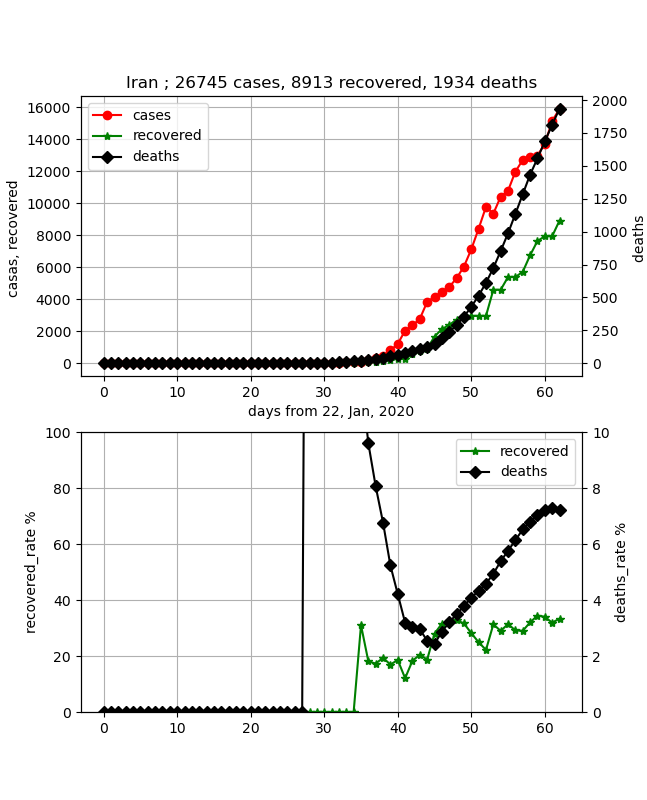
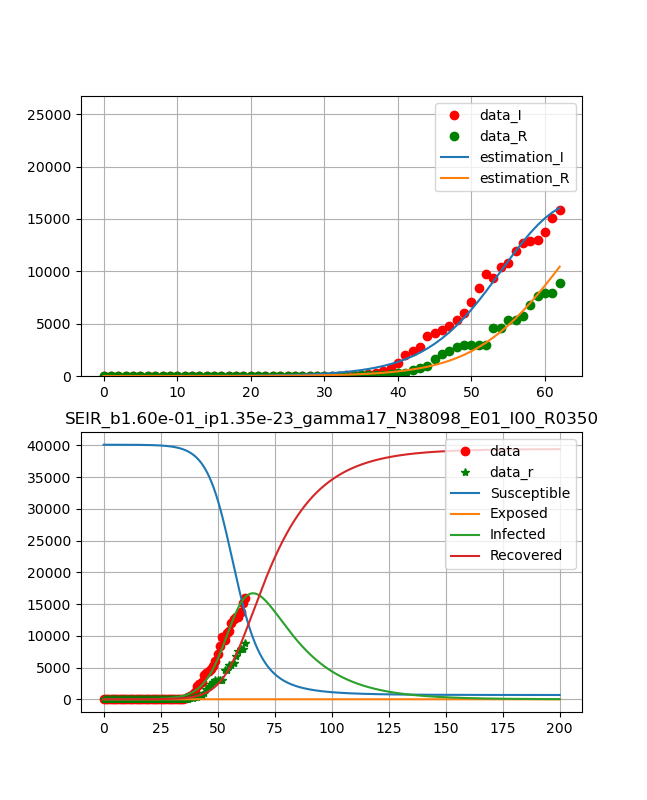
・韓国
なんだかちょっと前のデータと比べるといびつが目立ってきて、データの信ぴょう性が崩れてきた。
それでも全体としては治癒率が上がってきており、終息は比較的早そうである。

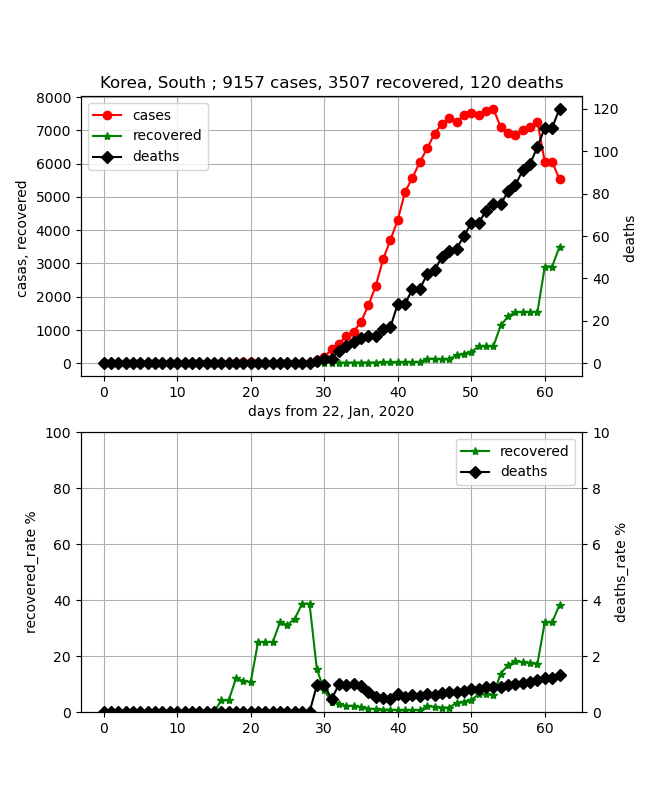
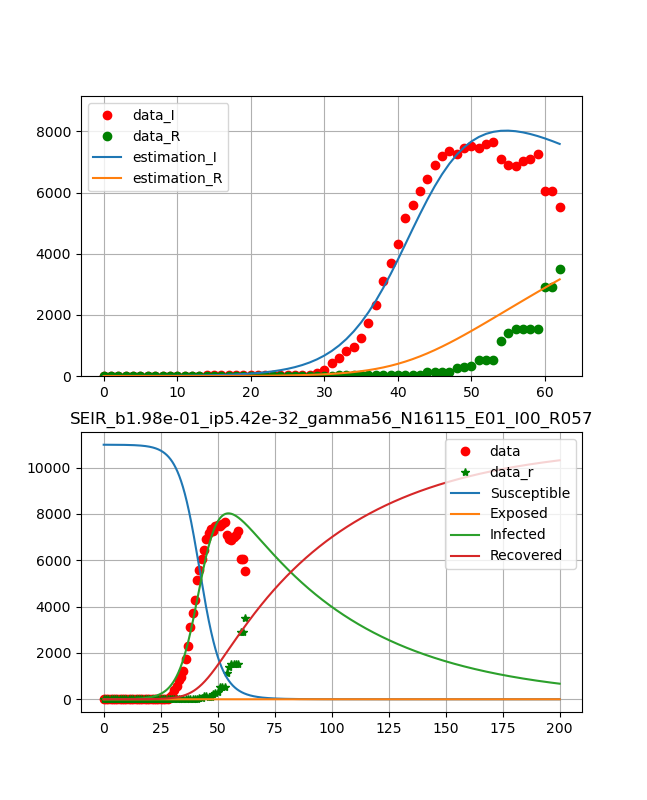
・イタリア
死亡率が極めて高く危険ではあるが、データはとても綺麗で洗練されている。したがって、フィッティングもしやすく、綺麗に乗った。まだまだ治癒率10%程度であり、少し時間（治癒ピークが2か月）はかかりそうだがこの後ピークが見えてくれば終息は近い。

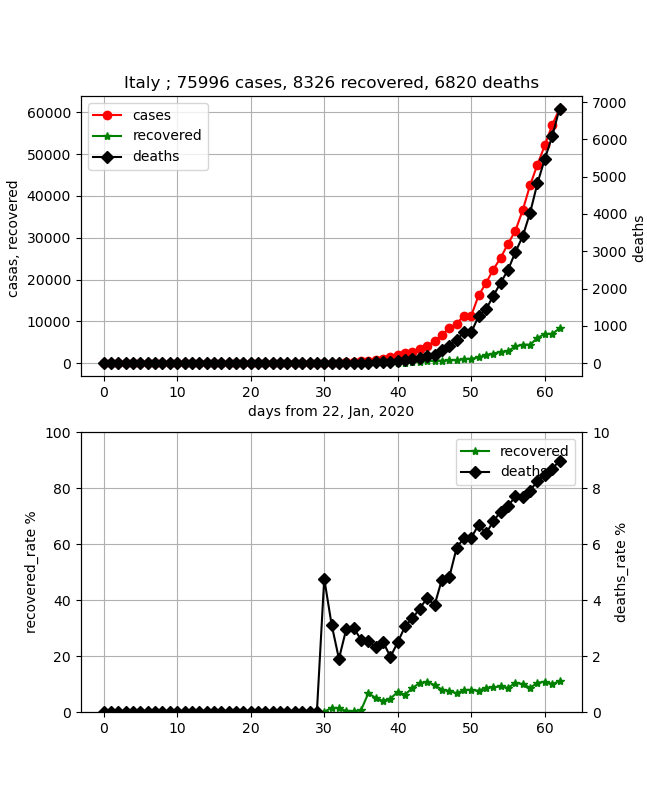
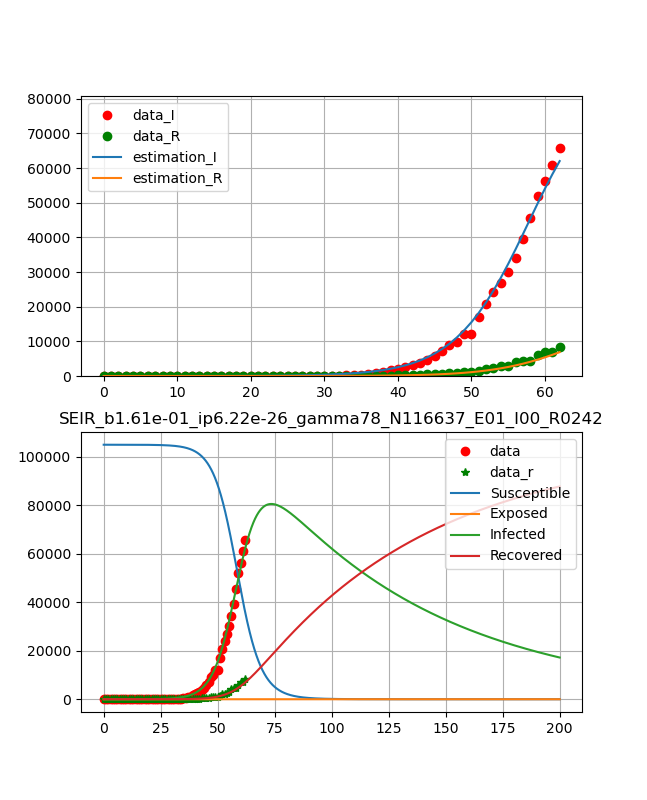
以下は、初期拡大期であり、フィッティング精度が悪くあてにならなそうだが掲載しておく。
・スペイン
もっともっと立ち上がっているが、合わせるのが難しい。


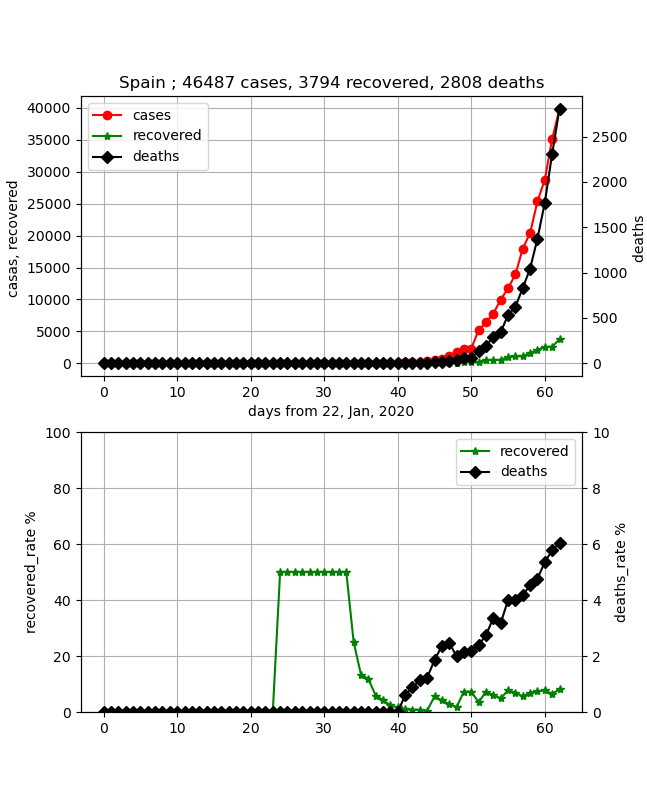
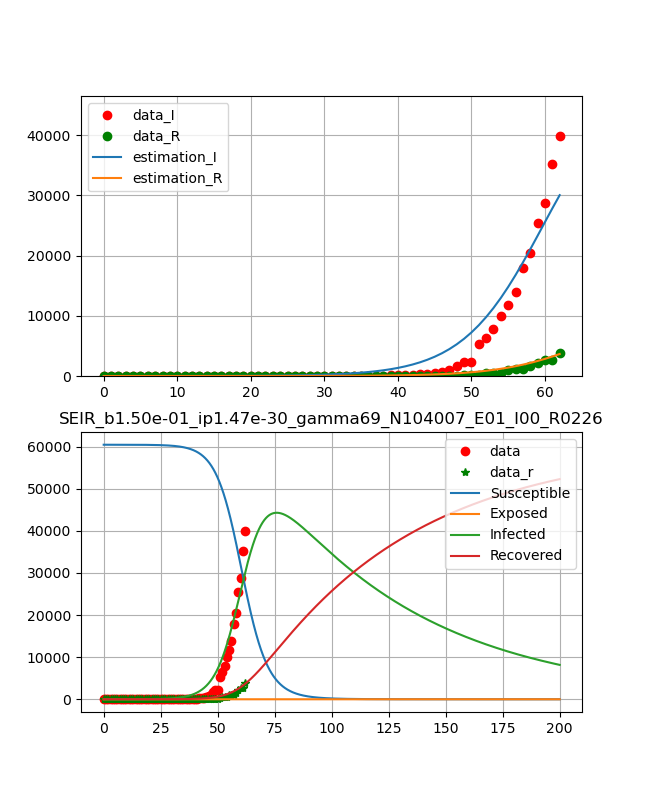
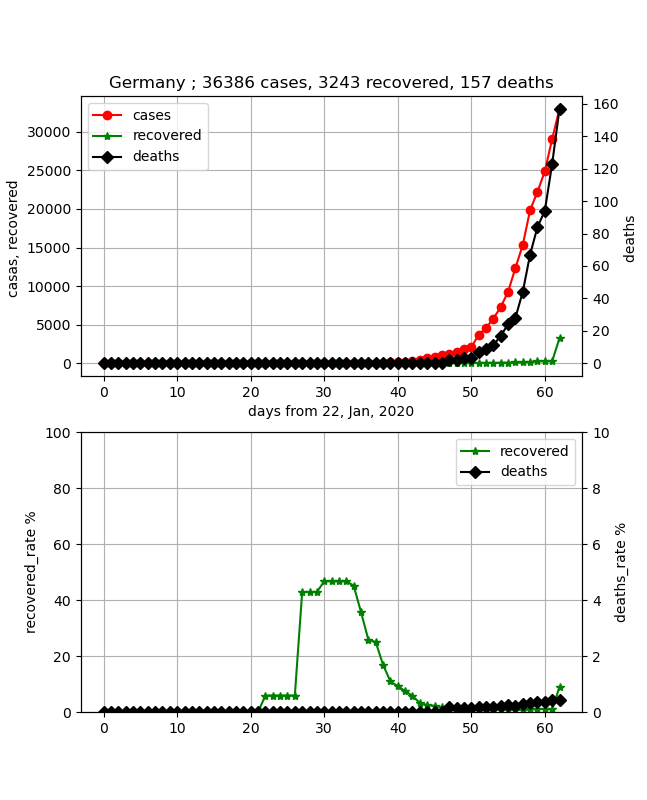
・ドイツ
こちらもまだまだできていないし、そもそも治癒数が少なすぎて初期拡大期だと思われる。

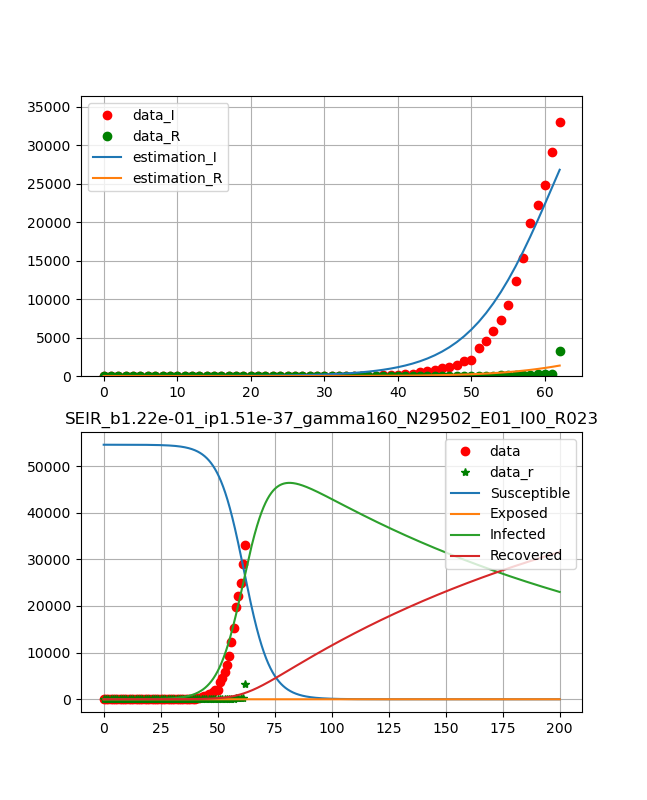
まとめ

・COVID-19データをフィッティングしてみた
・日本、イラン、韓国が中国に引き続いて終息が見えるようになると思われる
・他の欧米はまだまだ拡大期であり、終息予想は困難な状況である。

・今回はおおざっぱな話をしたが、日々の更新を見つつ、もう少し緻密な分析をしたいと思う

おまけ

武漢の同時フィッティングは以下のとおり
武漢のデータはこのモデルでは説明できないようだ（＞＜）
元データ

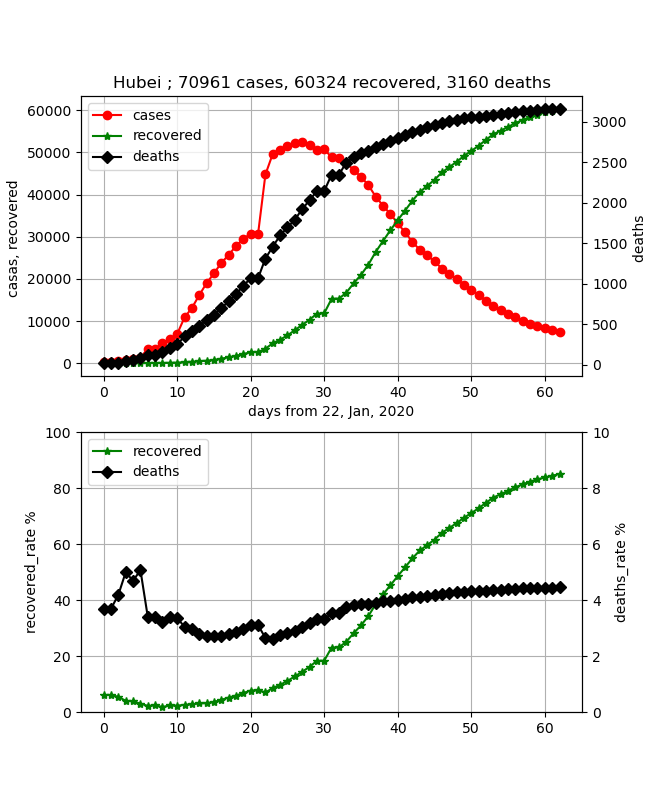
感染データのみフィッティング

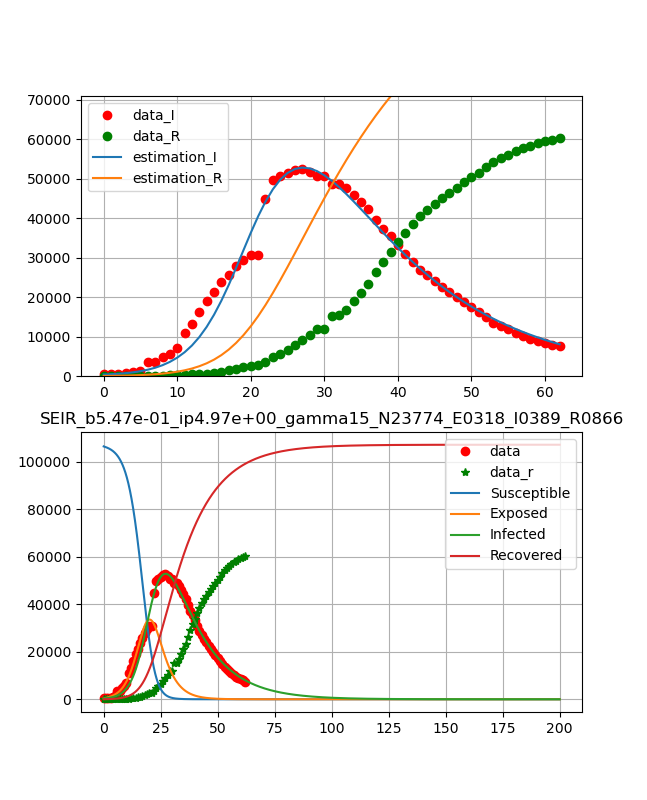
治癒データのみフィッティング

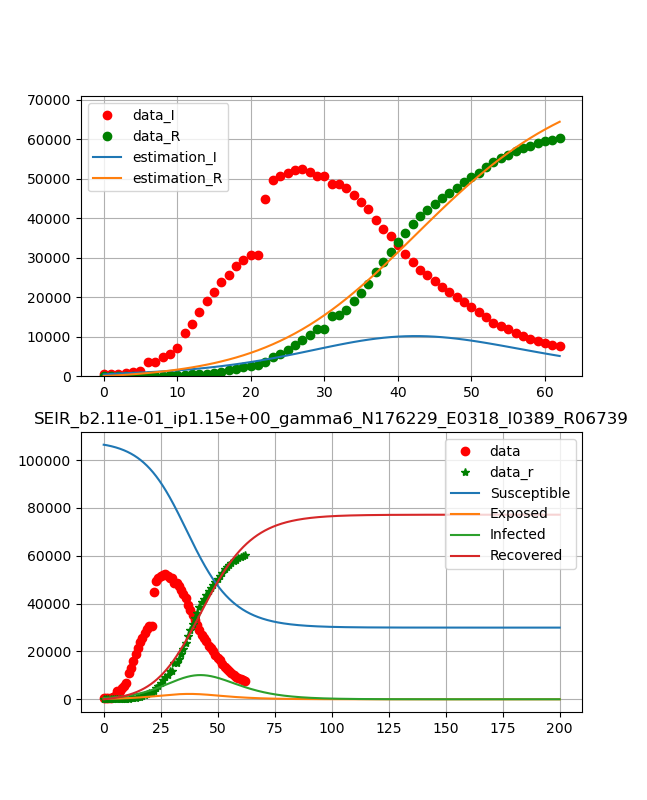
感染データおよび治癒データをフィッティング