COVID-19のデータ解析する準備として、以下のグラフを出力するまでの解説をする。
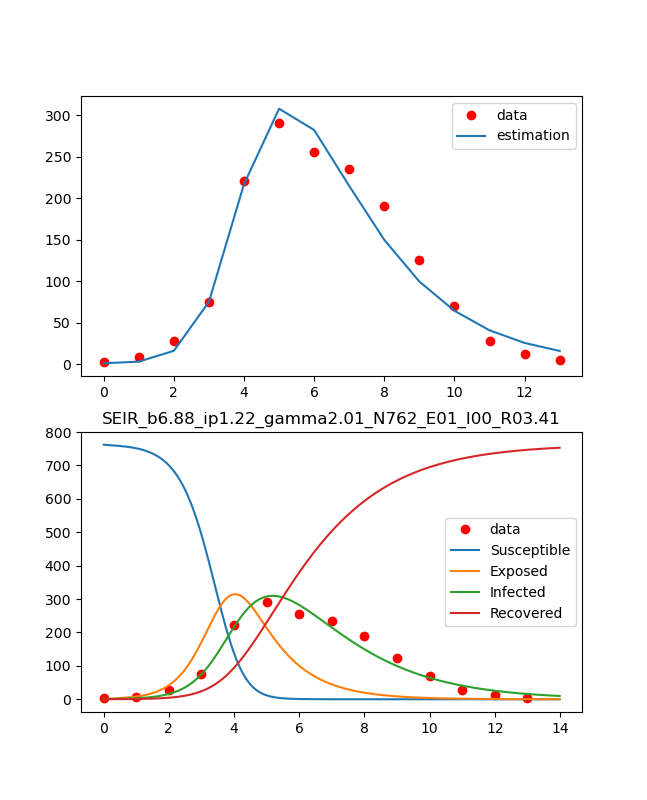
この図は、与えられたdataに対して感染症のSEIRモデルにminimize@scipyを利用してフィッティングした図である。
手法は、ほぼ以下の参考のとおりです。どちらもいろいろな意味で参考になりました。
【参考】
①感染症数理モデル事始め PythonによるSEIRモデルの概要とパラメータ推定入門
②感染病の数学予測モデル (SIRモデル):事例紹介(1)
③SEIRモデルで新型コロナウイルスの挙動を予測してみた。
やったこと
・コード解説
・SIRモデルとSEIRモデルでフィッティングしてみる
・その他のモデル
・コード解説
コード全体は以下に置いた。
・collective_particles/minimize_params.py
解説は上記の参考に譲り、ここでは今回利用したコードの解説をする。なお、データは参考②から利用させていただいた。また、minimizeのコードは参考①を参考にさせていただいた。
利用するLibは以下のとおりである。
今回はWindows10のconda環境のkeras-gpu環境で実施しているが、scipyも含めて以前インストール済である。
# include package
import numpy as np
from scipy.integrate import odeint
from scipy.optimize import minimize
import matplotlib.pyplot as plt
以下にSEIRモデルの微分方程式を定義している。
ここでNをどうするかは適宜判断することになるが、今回の命題では参考②の掲出論文からN=763人であり、固定とした。
SEIRモデルの微分方程式は以下のとおり
ここで、参考①ではNを変数betaに押し込めてしまって、陽には表していないが、ウワン的には以下の式の方が分かりやすい。
以下は、参考③から引用させていただいた。
{\begin{align}
\frac{dS}{dt} &= -\beta \frac{SI}{N} \\
\frac{dE}{dt} &= \beta \frac{SI}{N} -\epsilon E \\
\frac{dI}{dt} &= \epsilon E -\gamma I \\
\frac{dR}{dt} &= \gamma I \\
\end{align}
}
上記を見ながら以下を見ると、まんまなので理解できると思う。
# define differencial equation of seir model
def seir_eq(v,t,beta,lp,ip):
N=763
a = -beta*v[0]*v[2]/N
b = beta*v[0]*v[2]/N-(1/lp)*v[1]
c = (1/lp)*v[1]-(1/ip)*v[2]
d = (1/ip)*v[2]
return [a,b,c,d]
まず、通常の微分方程式として初期値に基づいて解を求めている。
# solve seir model
N,S0,E0,I0=762,0,1,0
ini_state=[N,S0,E0,I0]
beta,lp,ip=6.87636378, 1.21965986, 2.01373496 #2.493913 , 0.95107715, 1.55007883
t_max=14
dt=0.01
t=np.arange(0,t_max,dt)
plt.plot(t,odeint(seir_eq,ini_state,t,args=(beta,lp,ip))) #0.0001,1,3
plt.legend(['Susceptible','Exposed','Infected','Recovered'])
plt.pause(1)
plt.close()
結果は以下のとおり、ここでパラメータを推定して変化させていけば大体のフィッティングはできるが複雑なものでは難しい。
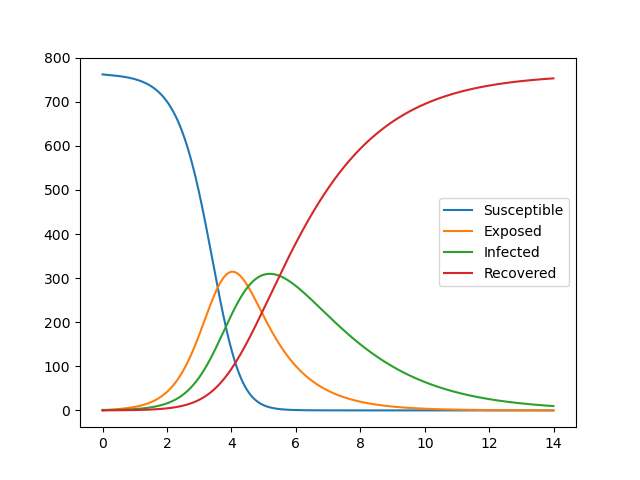
データは参考②のとおり、代入して以下のようにグラフに出力する。
# show observed i
# obs_i=np.loadtxt('fitting.csv')
data_influ=[3,8,28,75,221,291,255,235,190,125,70,28,12,5]
data_day = [1,2,3,4,5,6,7,8,9,10,11,12,13,14]
obs_i = data_influ
plt.plot(obs_i,"o", color="red",label = "data")
plt.legend()
plt.pause(1)
plt.close()
結果は以下のとおり、これは途中の確認のための出力なので見出しなどは省略している。
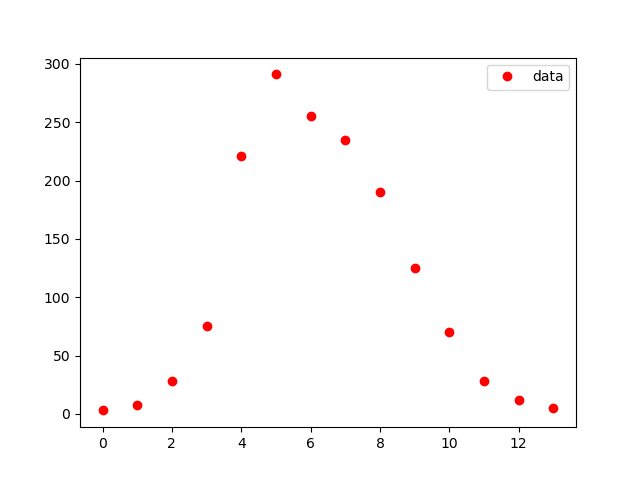
さて、次が推定部分である。この評価関数は引数の値を使って微分方程式で計算し、評価結果を返している。
# function which estimate i from seir model func
def estimate_i(ini_state,beta,lp,ip):
v=odeint(seir_eq,ini_state,t,args=(beta,lp,ip))
est=v[0:int(t_max/dt):int(1/dt)]
return est[:,2]
対数尤度関数を以下のように定義する。
※参考①を参照
基本はパラメータを変更して、この対数尤度関数の最大値を求める問題になる。(実際はマイナスを取って最小化問題にしている)
※ここでlogの引数が負になるのを防ぐために絶対値を取っている
# define logscale likelihood function
def y(params):
est_i=estimate_i(ini_state,params[0],params[1],params[2])
return np.sum(est_i-obs_i*np.log(np.abs(est_i)))
最大値を求めるために以下のScipyのminimize関数を利用する。
# optimize logscale likelihood function
mnmz=minimize(y,[beta,lp,ip],method="nelder-mead")
print(mnmz)
出力は以下のとおり
>python minimize_params.py
final_simplex: (array([[6.87640764, 1.21966435, 2.01373196],
[6.87636378, 1.21965986, 2.01373496],
[6.87638203, 1.2196629 , 2.01372646],
[6.87631916, 1.21964456, 2.0137297 ]]), array([-6429.40676091, -6429.40676091, -6429.40676091, -6429.4067609 ]))
fun: -6429.406760912483
message: 'Optimization terminated successfully.'
nfev: 91
nit: 49
status: 0
success: True
x: array([6.87640764, 1.21966435, 2.01373196])
計算結果から以下のようにbeta_const,lp,gamma_constを取り出し、以下でR0を計算する。これが基本再生産数であり、感染拡大の目安でありR0<1なら拡大しないが、R0>1なら拡大し、その程度を示す指標である。
# R0
beta_const,lp,gamma_const = mnmz.x[0],mnmz.x[1],mnmz.x[2] #感染率、感染待時間、除去率(回復率)
print(beta_const,lp,gamma_const)
R0 = beta_const*(1/gamma_const)
print(R0)
今回は以下のとおりとなり、R0=3.41なので感染拡大したわけですね。
6.876407637532918 1.2196643491443309 2.0137319643699927
3.4147581501415165
こうして求めたものをグラフに表示します。
# plot reult with observed data
fig, (ax1,ax2) = plt.subplots(2,1,figsize=(1.6180 * 4, 4*2))
lns1=ax1.plot(obs_i,"o", color="red",label = "data")
lns2=ax1.plot(estimate_i(ini_state,mnmz.x[0],mnmz.x[1],mnmz.x[2]), label = "estimation")
lns_ax1 = lns1+lns2
labs_ax1 = [l.get_label() for l in lns_ax1]
ax1.legend(lns_ax1, labs_ax1, loc=0)
lns3=ax2.plot(obs_i,"o", color="red",label = "data")
lns4=ax2.plot(t,odeint(seir_eq,ini_state,t,args=(mnmz.x[0],mnmz.x[1],mnmz.x[2])))
ax2.legend(['data','Susceptible','Exposed','Infected','Recovered'], loc=0)
ax2.set_title('SEIR_b{:.2f}_ip{:.2f}_gamma{:.2f}_N{:d}_E0{:d}_I0{:d}_R0{:.2f}'.format(beta_const,lp,gamma_const,N,E0,I0,R0))
plt.savefig('./fig/SEIR_b{:.2f}_ip{:.2f}_gamma{:.2f}_N{:d}_E0{:d}_I0{:d}_R0{:.2f}_.png'.format(beta_const,lp,gamma_const,N,E0,I0,R0))
plt.show()
plt.close()
結果は上記のとおりです。
・その他のモデル
この計算をやっていたら、もう少し簡単なSIRモデルと少し複雑なモデルがあったのでまとめておきます。
SIRモデルは、S-E-I-RからExposedを無視したモデルなので以下のとおりです。
{\begin{align}
\frac{dS}{dt} &= -\beta \frac{SI}{N} \\
\frac{dI}{dt} &= \beta \frac{SI}{N} -\gamma I \\
\frac{dR}{dt} &= \gamma I \\
\end{align}
}
以下のように書き換えると$R_0$の意味が理解できる。
{\begin{align}
\frac{dS}{dt} &= -R_0 \frac{S}{N} \frac{dR}{dt} \\
R_0 &= \frac{\beta}{\gamma}\\
\frac{dI}{dt} &= 0 \ のとき感染者ピーク\\
R_0 &= \frac{\beta}{\gamma}= \frac{N}{S_0} \\
\end{align}
}
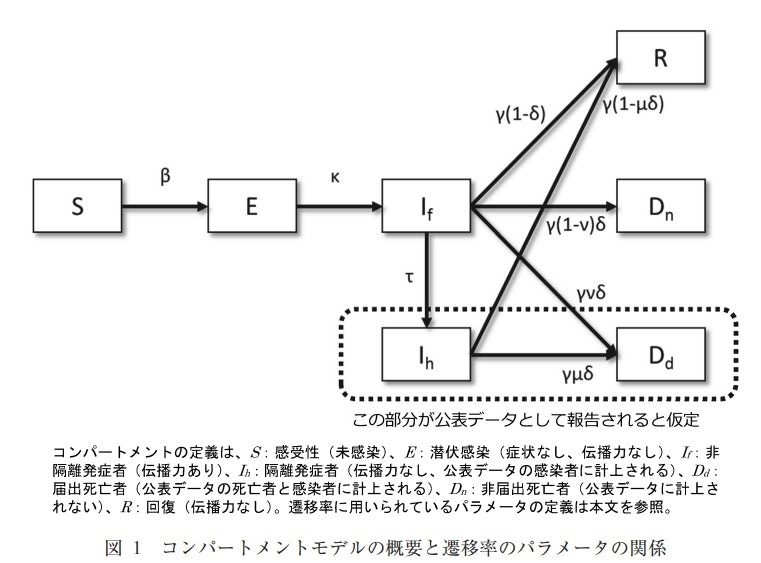
一方、例えば死亡する遷移があり、届け出無しの死亡とかあるなど複雑な状況だと以下のようになります。なお、死亡者は感染には寄与しないという仮定です。
※COVID-19はこんな感じかもしれない
図は参考①の以下の文献より
・数理モデルを用いたエボラウイルス感染症の流行の解析

まとめ
・minimize@scipyにより自動的にデータフィッティングできるようになった
・SEIRモデルで実際のデータをフィッティング出来た
・次回はCOVID-19の各国のデータを分析したいと思う