今回は、回帰を取り上げようと思う。
※前半は問題ありませんが、3Dのpredictionの部分のコードにバグがあったので、バグフィックス版を別途書きました
超簡単なSVMの理論
回帰と言えば、通常は(系を表していると考えられるモデルに基づいて導出された)適当な関数を仮定して、そのパラメーターや次数を最小二乗法などでフィッティングする。
しかし、機械学習では、関数を仮定するのではなく、超平面で空間内の点を分類することにより、目的関数の最大化を実施する。
そして、scikit-learnだけでも多くの種類があることが参考③を見ればわかる。
今回は、理論を少し書こうかなと考えたが、参考①がほぼオリジナルの解説であり、さらに参考②をじっくり読んでいただいた方が理解は速いと思う。
ここでは、かなり省略しつつ、必要な式だけ抜粋してパラメーターの意味などを見るにとどめることとする。、
まず、SVMは以下のような線形しきい素子を用いて、2 クラスのパターン識別器を構成する手法である。
※図は全て参考②による
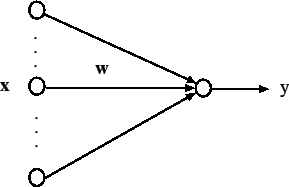
このとき、識別関数は以下のとおり書け、2値を出力する。
y=sign(w^Tx-h) \\
関数 sign(u) は、u > 0 のとき 1 をとり、u ≤ 0 のとき−1 をとる
この様子は、以下の図のように、空間内にH1とH2という超平面を構成し、点群$x$を二つのクラスに分離する。
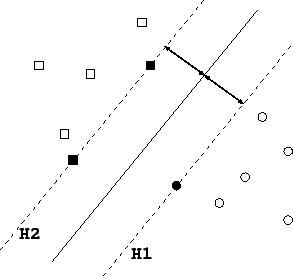
そして、SVMでは上図のようにマージンというH1とH2の隙間を最大化するように識別平面を求める。もし、訓練サンプル集合が分離可能なら、
t_i(w^Tx-h) \geq 1, i=1,...,N
を満たすパラメータが存在する。したがって、マージン最大化の問題は、上式を制約条件として以下の目的関数を最大化する問題に帰着する。
L(w)=\frac{1}{2}w^Tw
これからSVMはLagrange乗数$\alpha_i(\geq0), i=1,...,N$とすると、以下の目的関数を最大化する最適化問題に帰する。
L(w,h,\alpha)=\frac{1}{2}w^Tw-\sum_{i=1}^{N}\alpha_i\left\{t_i(w^Tx_i-h)-1\right\}
パラメータ w および h に関する偏微分から停留点では、以下が成り立つ。
w=\sum_{i=1}^{N}\alpha_it_ix_i \\
0=\sum_{i=1}^{N}\alpha_it_i
したがって、上記の目的関数は以下の目的関数となり、SVMは
\sum_{i=1}^{N}\alpha_it_i=0 \\
0\leq \alpha_i, i= 1,...,N
の制約の下で、以下の目的関数を最大化する双対問題となる。
L_D(\alpha)=\sum_{i=1}^{N}\alpha_i - \frac{1}{2}\sum_{i,j=1}^{N}\alpha_i\alpha_jt_it_jx_i^Tx_j
以下参考②からの完全引用である。
「その解で $α^∗_i$ が 0 でない、すなわち、$α^∗_i > 0$ となる訓練サンプル $x_i$ は、先の2つの 超平面 $w^Tx−h = 1$ か $w^Tx−h = −1$ のどちらかにのっている。このことから、$α^∗_i$ が 0 でない 訓練サンプル $x_i$ のことを「サポートベクター」と呼んでいる。これが、サポートベクターマシン の名前の由来である。直感的に理解できるように、一般には、サポートベクターは、もとの訓練サ ンプル数に比べてかなり少ない。つまり、沢山の訓練サンプルの中から小数のサポートベクターを 選び出し、それらのみを用いて線形しきい素子のパラメータが決定されることになる。 」
【参考】
①A tutorial on support vector regression (2004)
②サポートベクターマシン入門
③1.4.7.3. SVR@scikit-learn
④第9回 サポートベクターマシンで非線形な競馬予測に挑む
【追記15/02/2019】超簡単なSVRの理論
SVRの理論については、もちろん上記参考の①③にも記載されているが、中身が今一つわからないので気持ち悪い。ということで、明快にご説明されている資料があったので、ご紹介します。
【参考:追記】
・サポートベクター回帰(Support Vector Regression, SVR)@データ化学工学研究室(金子研究室)@明治大学 理工学部 応用化学科
主な式を引用すると以下のとおり、
※よく見ると、原論文(参考①)とほぼ同一な導出でした(以下は導出式を原論文に合わせました)
L(w)=\frac{1}{2}w^Tw + C\sum_{i=1}^{N}h(y^{i}-f(x_i))
を最小化する。
$h$;誤差関数
$C$;二つの項のバランスを決める係数
$n$;サンプル数
誤差の不感帯$\epsilon$を導入して、誤差関数を以下とおく。
※この不感帯が上記のマージンに対応する
h(y^{i}-f(x^{(i)}))=max(0,|y^{i}-f(x^{(i)})|-\epsilon)
SVMと同様にスラック変数$\zeta _{i}\geq0$,$\ \zeta _{i}^{*} \geq0$を導入する。
y^{i}-f(x_i)\geq \epsilon+\zeta _i \\
y^{i}-f(x_i)\leq -\epsilon-\zeta ^{*}_i \\
上式は、以下となる。
L(w)=\frac{1}{2}w^Tw + C\sum_{i=1}^{N}(\zeta _i+\zeta ^{*}_i)
ここで、Lagrange乗数
\alpha _i , \alpha _i^{*} , \beta _i , \beta _i^{*} (\geq 0) , i=1,...,N
を導入すると、以下の$L$を
w,b,\zeta_i,\zeta_i^{*}について最小化し、\\
\alpha_i,\alpha_i^{*},\beta_i,\beta_i^{*}について最大化する
L(w,\epsilon , \zeta ,\zeta ^{*},...)=\frac{1}{2}w^Tw + C\sum_{i=1}^{N}(\zeta _i+\zeta ^{*}_i)-C\sum_{i=1}^{N}(\beta_i\zeta _i+\beta_i^{*}\zeta _i^{*})\\
-\sum_{i=1}^{N}(\alpha_i(\epsilon+\zeta _i+y^{(i)}-f(x^{(i)}))-\sum_{i=1}^{N}(\alpha_i^{*}(\epsilon+\zeta _i^{*}-y^{(i)}+f(x^{(i)}))
SVMと同じように、停留点での$w,b,\zeta_i,\zeta_i^{*}$の偏微分=0から以下がなりたつ
※ここで$x⇒\phi (x)$であり、SVMの変形を参考にしてください
※ここで原論文(参考①)の式1より$f(x_i)=wx_i+b$である。
w=\sum_{i=1}^{N}(\alpha _i- \alpha _i^{*})\phi (x^{(i)})^T \\
\sum_{i=1}^{N}(\alpha _i- \alpha _i^{*})=0 \\
\alpha _i+\beta _i =C\ (i=1,...,N) \\
\alpha ^{*}_i+\beta ^{*}_i =C\ (i=1,...,N)
これを上式に代入すると、
L=-\frac{1}{2}\sum _{i=1}^{N}\sum _{j=1}^{N}(\alpha _i-\alpha _i^{*})(\alpha _j-\alpha _j^{*})K(x^{(i)},x^{(j)}) - \epsilon \sum _{i=1}^{N}(\alpha _i+\alpha _i^{*}) +\sum _{i=1}^{N}(\alpha _i-\alpha _i^{*})y_i
したがって、上式を
0\leq \alpha _i\leq C , 0 \leq \alpha _i ^{*} \leq C
の制約のもと最大化すれば、$\alpha _i, \alpha _i^{*}$が求まり、
f(x^{(j)})=\sum _{i=1}^{N}(\alpha _i-\alpha _i^{*})K(x^{(i)},x^{(j)}) + b
が求まる。
ここで
K(x^{(i)},x^{(j)})=\phi (x^{(i)})\phi (x^{(j)})^T
は、カーネル関数であり、以下のような関数が使われ、カーネルマジックという手法が使われる。
・線形カーネル
K(x^{(i)},x^{(j)})= (x^{(i)}) (x^{(j)})^T
・Gaussianカーネル
※このカーネルが以下でRBF(Radial Basis Function)と呼ばれているものである
K(x^{(i)},x^{(j)})=exp(-\gamma |x^{(i)}-x^{(j)}|^2)
・多項式カーネル
K(x^{(i)},x^{(j)})= (1+ \lambda(x^{(i)}) (x^{(j)})^T)^d
【参考】
・RBFネットワーク(Radial Basis Function Network)
やったこと
・scikit-learnの回帰を試してみる
・SVMで多変量回帰をやって3D描画してみる
・scikit-learnの回帰を試してみる
ということで、今回は以下のとおり1次元問題$y=f(x)$に対して、scikit-learnで試せるなるべく多くの回帰手法を試してみた。
【参考】
・Miscellaneous examples@scikit-learn v0.20.2
・SVMを使って回帰してみる
利用したものをimportしている。
import numpy as np
import random
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn import datasets, metrics
from sklearn.svm import LinearSVR
from sklearn import linear_model
from sklearn.neighbors import KNeighborsRegressor
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, WhiteKernel
from sklearn import linear_model
最初に$tanh(x)$を確認したあと、少しずつ関数を変更して試してみた。
X = np.arange(-6, 6, 0.1)
# y = np.tanh(X)
y = np.sin(X)*np.tanh(X)+0.6*X-0.6
描画は一応、3面書くこととした。
元々の関数をすべてのplotに描画して比較できるようにした。
fig=plt.figure(figsize=(12, 10))
ax1 = fig.add_subplot(311)
ax2 = fig.add_subplot(312)
ax3 = fig.add_subplot(313)
ax1.set_title('Hyperbolic Tangent Graph')
ax1.plot(X,y,label="original function")
ax2.plot(X,y,label="original function")
ax3.plot(X,y,label="original function")
ノイズも載せた。
e = [random.gauss(0, 0.3) for i in range(len(y))]
y += e
ax1.set_title('Hyperbolic Tangent Scatter')
ax1.scatter(X, y,label="original ")
ax3.set_title('Linear&Poly predict')
ax3.scatter(X, y,label="original ")
# 列ベクトルに変換する
X = X[:, np.newaxis]
学習は以下のとおり、同時に実施している。
# 学習を行う
# svr = svm.SVR(kernel='rbf')
# Lsvr = LinearSVR(random_state=0, tol=1e-5)
# lSGDR = linear_model.SGDRegressor(max_iter=1000, tol=1e-3)
KNR = KNeighborsRegressor(n_neighbors=5)
kernel = 1.0 * RBF(length_scale=100.0, length_scale_bounds=(1e-2, 1e3)) \
+ WhiteKernel(noise_level=1, noise_level_bounds=(1e-10, 1e+1))
GPR = GaussianProcessRegressor(kernel=kernel, alpha=0.0)
# RBFカーネル、線形、多項式でフィッティング
svr = svm.SVR(kernel='rbf', C=1e3, gamma=0.1)
Lsvr = svm.SVR(kernel='linear', C=1e3)
Psvr = svm.SVR(kernel='poly', C=1e3, degree=2)
lRidge = linear_model.Ridge(alpha=.5)
lBRidge = linear_model.BayesianRidge()
svr.fit(X, y)
KNR.fit(X, y)
GPR.fit(X, y)
Lsvr.fit(X, y)
Psvr.fit(X, y)
lRidge.fit(X, y)
lBRidge.fit(X, y)
描画で間違わないようにラベルをつけて、凡例に反映した。
過去と未来予測もしたいので、計算範囲を(-10,10)とした。
# 回帰曲線を描く
X_plot = np.linspace(-10, 10, 10000)
y_svr = svr.predict(X_plot[:, np.newaxis])
y_KNR = KNR.predict(X_plot[:, np.newaxis])
y_GPR = GPR.predict(X_plot[:, np.newaxis])
y_Lsvr = Lsvr.predict(X_plot[:, np.newaxis])
y_Psvr = Psvr.predict(X_plot[:, np.newaxis])
y_lRidge = lRidge.predict(X_plot[:, np.newaxis])
y_lBRidge = lBRidge.predict(X_plot[:, np.newaxis])
# グラフにプロットする。
ax2.set_title('svm'+' predict')
ax2.scatter(X, y,label="original ")
ax2.plot(X_plot, y_svr,"r",label="SVR")
ax2.plot(X_plot, y_KNR,"b",label="KNR")
ax3.plot(X_plot, y_GPR,"g",label="GPR")
ax3.plot(X_plot, y_Lsvr,"r",label="SVR_Linear")
ax2.plot(X_plot, y_Psvr,"b",label="SVR_Poly")
ax3.plot(X_plot, y_lRidge,"g",label="Linear_Ridge")
ax3.plot(X_plot, y_lBRidge,"k",label="Bayesian_Ridge")
ax1.legend() # 凡例をグラフにプロット
ax2.legend() # 凡例をグラフにプロット
ax3.legend() # 凡例をグラフにプロット
plt.savefig("sin(X)tanh(X)+06X-06_reg.jpg")
plt.show()
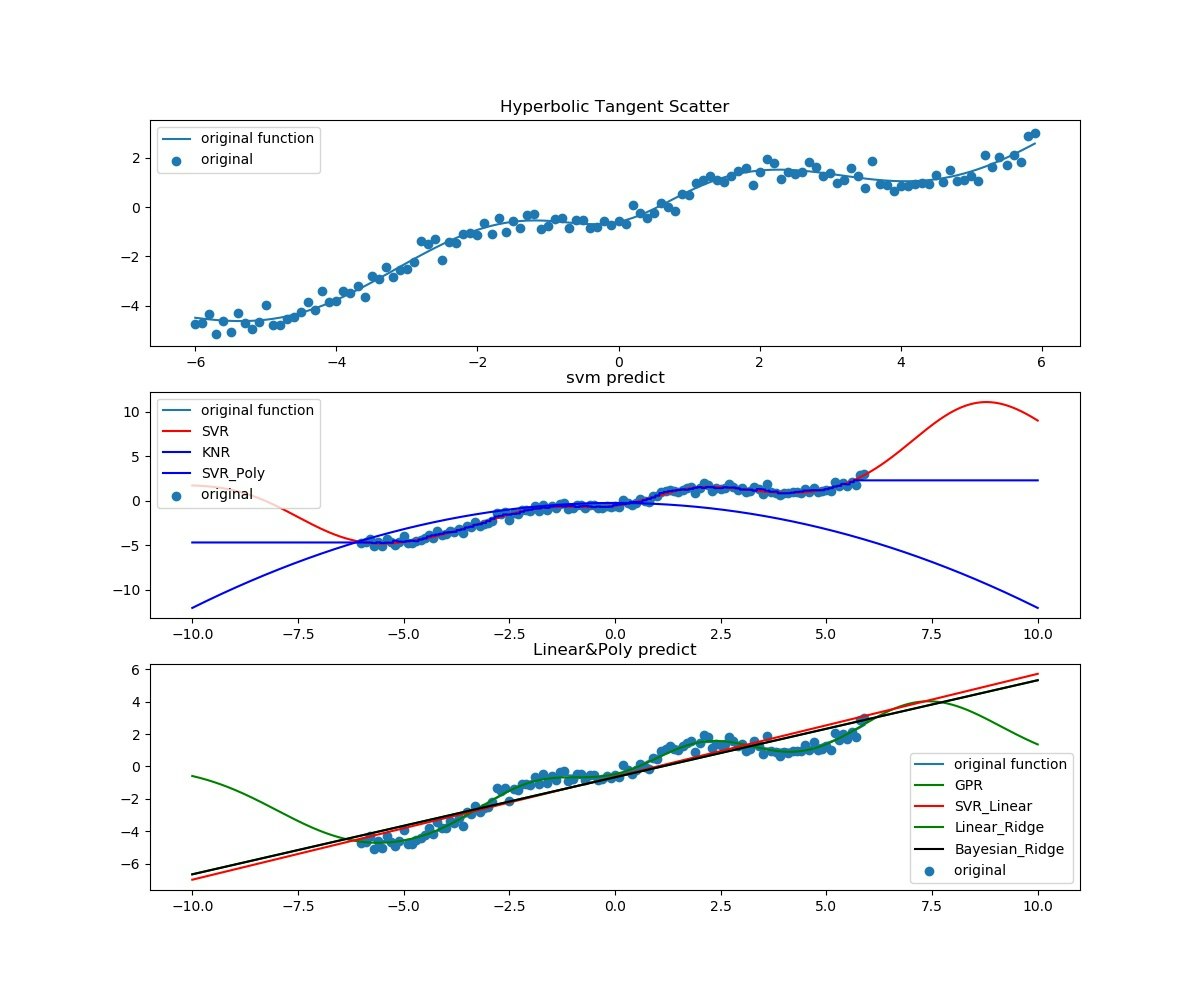
結果は以下のとおり、
最初はほぼ単調な$tanh(x)$。過去と未来予測はできているだろうか。
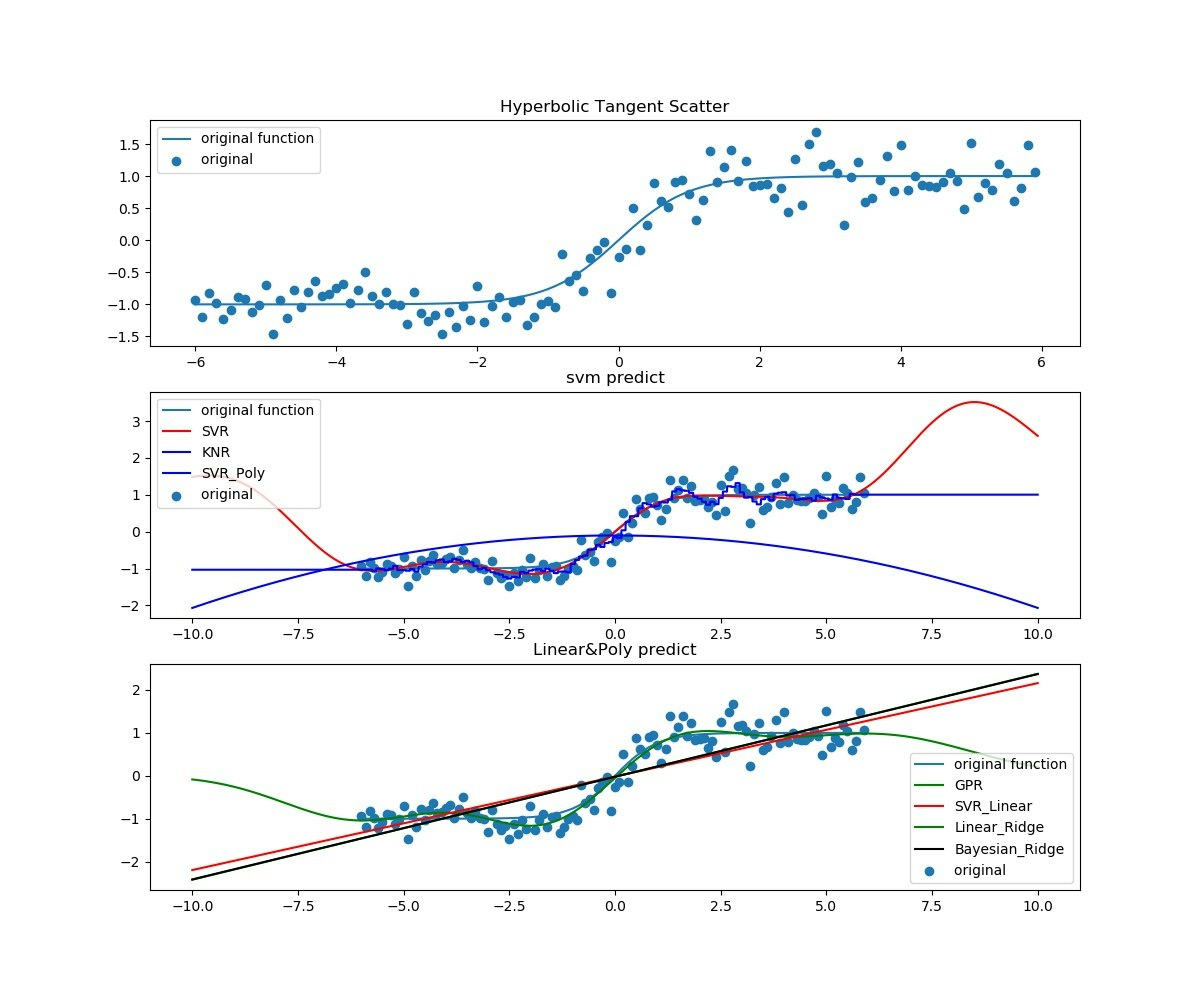
次に$sin(x)*tanh(x)$。過去も未来も予測できているとは言えない。
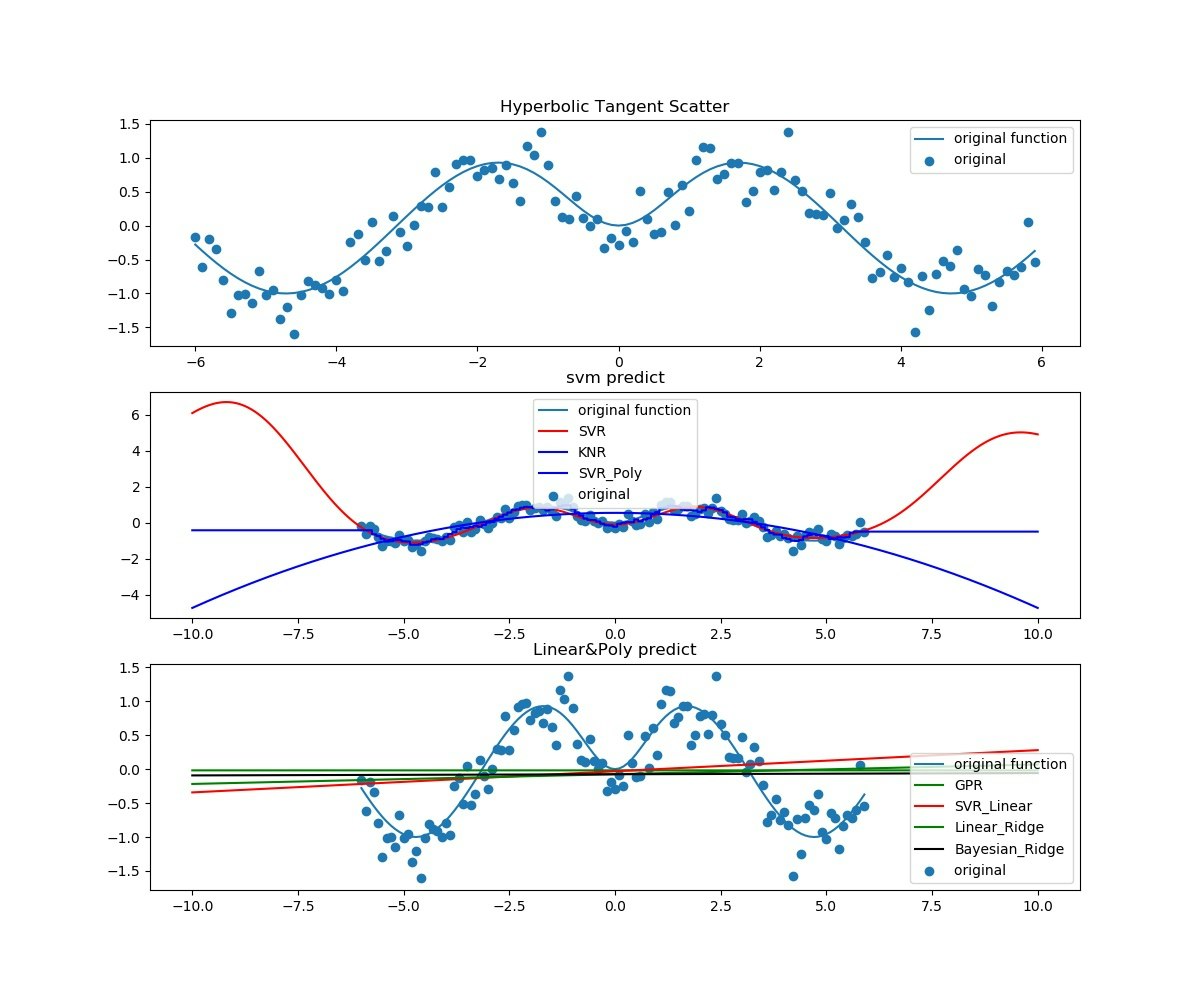
最後に、少し勾配を持たせて$sin(x)*tanh(x)+0.6x-6$。これもできているとは言えないがなんとなく線形フィッティングや近い過去や未来についてはGPRやSVRはできていると言えるかもしれない。
・SVMで多変量回帰をやって3D描画してみる
これは、参考⑤を再現するのはすぐできたが、どうにも不満だったので、参考⑥を参考にしつつ、次元減らして3Dプロットしてみた。
※ある意味、実感できた。
【参考】
・⑤scikit-learnで多変数の回帰モデル - SVRの比較検証やってみた
・⑥matplotlibで3Dプロット
利用しているものは、最後の二つが目新しい。
import numpy as np
from sklearn.svm import SVR
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
from mpl_toolkits.mplot3d import Axes3D
次元は(x、y)の二次元と関数値の3Dプロットである。
参考⑥のとおり、平均と標準偏差の次元を与えている。
m = 2 #dimension
mean = np.zeros(m)
sigma = np.eye(m)
(x,y)は100x100とした。
※あまり大きいとなかなか終了しないし、小さいとガタガタする。
N = 100
x1 = np.linspace(-5, 5, N)
x2 = np.linspace(-5, 5, N)
X1, X2 = np.meshgrid(x1, x2)
X = np.c_[np.ravel(X1), np.ravel(X2)]
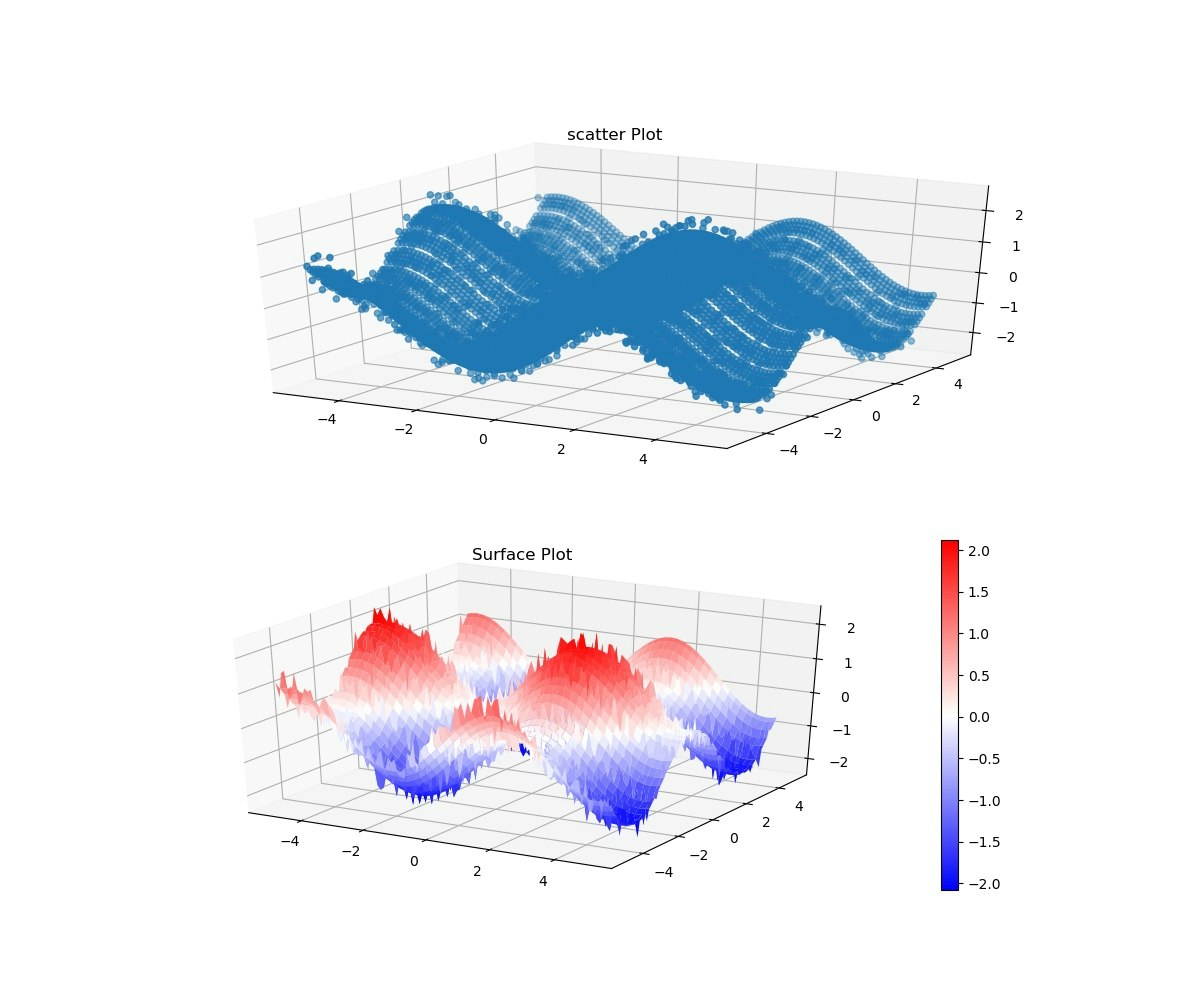
scatterはそのまま描画できるが、surfaceだとy1のようにreshapeが必要。
# アウトプットを算出
y = np.sin(X1).ravel()+ np.cos(X2).ravel()
y_o = y.copy()
y1 = y.reshape(X1.shape)
ノイズのせるのも(20,100)。
# Y_plot = multivariate_normal.pdf(x=X, mean=mean, cov=sigma)
# Y_plot = Y_plot.reshape(X1.shape)
# ノイズを加える
y1[::5] += 1 * (0.5 - np.random.rand(20,100))
描画は2象限とし、scatterとsurfaceを描いた。
fig=plt.figure(figsize=(12, 10))
ax1 = fig.add_subplot(211, projection='3d')
ax2 = fig.add_subplot(212, projection='3d')
surf = ax2.plot_surface(X1, X2, y1, cmap='bwr', linewidth=0) #Y_plot
fig.colorbar(surf)
ax1.scatter3D(np.ravel(X1), np.ravel(X2), y)
ax2.set_title("Surface Plot")
ax1.set_title("scatter Plot")
plt.savefig('Surface_plot2_input.jpg')
plt.pause(1)
plt.close()
以下でフィッティング
# フィッティング
svr_rbf = SVR(kernel='rbf', C=1e3, gamma=0.1)
# svr_lin = SVR(kernel='linear', C=1e3)
# svr_poly = SVR(kernel='poly', C=1e3, degree=3)
y_rbf = svr_rbf.fit(X, y).predict(X)
# y_lin = svr_lin.fit(X, y).predict(X)
# y_poly = svr_poly.fit(X, y).predict(X)
以下、(-5,5)で検証描画
# テストデータも準備
# test_X1 = np.sort(5 * np.random.rand(40, 1).reshape(40), axis=0)
# test_X2 = np.sort(3 * np.random.rand(40, 1).reshape(40), axis=0)
N = 100
test_x1 = np.linspace(-5, 5, N)
test_x2 = np.linspace(-5, 5, N)
test_X1, test_X2 = np.meshgrid(test_x1, test_x2)
test_X = np.c_[np.ravel(test_X1), np.ravel(test_X2)]
# test_X = np.c_[test_X1, test_X2]
# test_y = np.sin(test_X1).ravel() + np.cos(test_X2).ravel()
# テストデータを突っ込んで推定してみる
test_rbf = svr_rbf.predict(test_X)
# test_lin = svr_lin.predict(test_X)
# test_poly = svr_poly.predict(test_X)
test_rbf1 = test_rbf.reshape(test_X1.shape)
fig=plt.figure(figsize=(12, 10))
ax1 = fig.add_subplot(211, projection='3d')
ax2 = fig.add_subplot(212, projection='3d')
# ax3 = fig.add_subplot(313)
ax1.set_title('Graph')
ax1.scatter3D(np.ravel(test_X1), np.ravel(test_X2), test_rbf)
surf = ax2.plot_surface(test_X1, test_X2, test_rbf1, cmap='bwr', linewidth=0) #Y_plot
fig.colorbar(surf)
# ax1.scatter3D(np.ravel(test_X1), np.ravel(test_X2), test_lin)
# ax1.scatter3D(np.ravel(test_X1), np.ravel(test_X2), test_poly)
plt.savefig('Surface_svr_rbf_prediction.jpg')
plt.pause(1)
plt.close()
以下検証。検証は相関係数(入力データと予測データ)と平均二乗誤差の平方根(root mean squared error)
from sklearn.metrics import mean_squared_error
from math import sqrt
# 元関数と検証する
test_y = np.sin(test_X1).ravel() + np.cos(test_X2).ravel()
# 相関係数計算
rbf_corr = np.corrcoef(test_y, test_rbf)[0, 1]
# lin_corr = np.corrcoef(test_y, test_lin)[0, 1]
# poly_corr = np.corrcoef(test_y, test_poly)[0, 1]
# RMSEを計算
rbf_rmse = sqrt(mean_squared_error(test_y, test_rbf))
# lin_rmse = sqrt(mean_squared_error(test_y, test_lin))
# poly_rmse = sqrt(mean_squared_error(test_y, test_poly))
print( "RBF: RMSE %f \t\t Corr %f" % (rbf_rmse, rbf_corr))
# print( "Linear: RMSE %f \t Corr %f" % (lin_rmse, lin_corr))
# print( "Poly: RMSE %f \t\t Corr %f" % (poly_rmse, poly_corr))
入力データ(ノイズがのっている)
予測データ(ノイズが消えた)
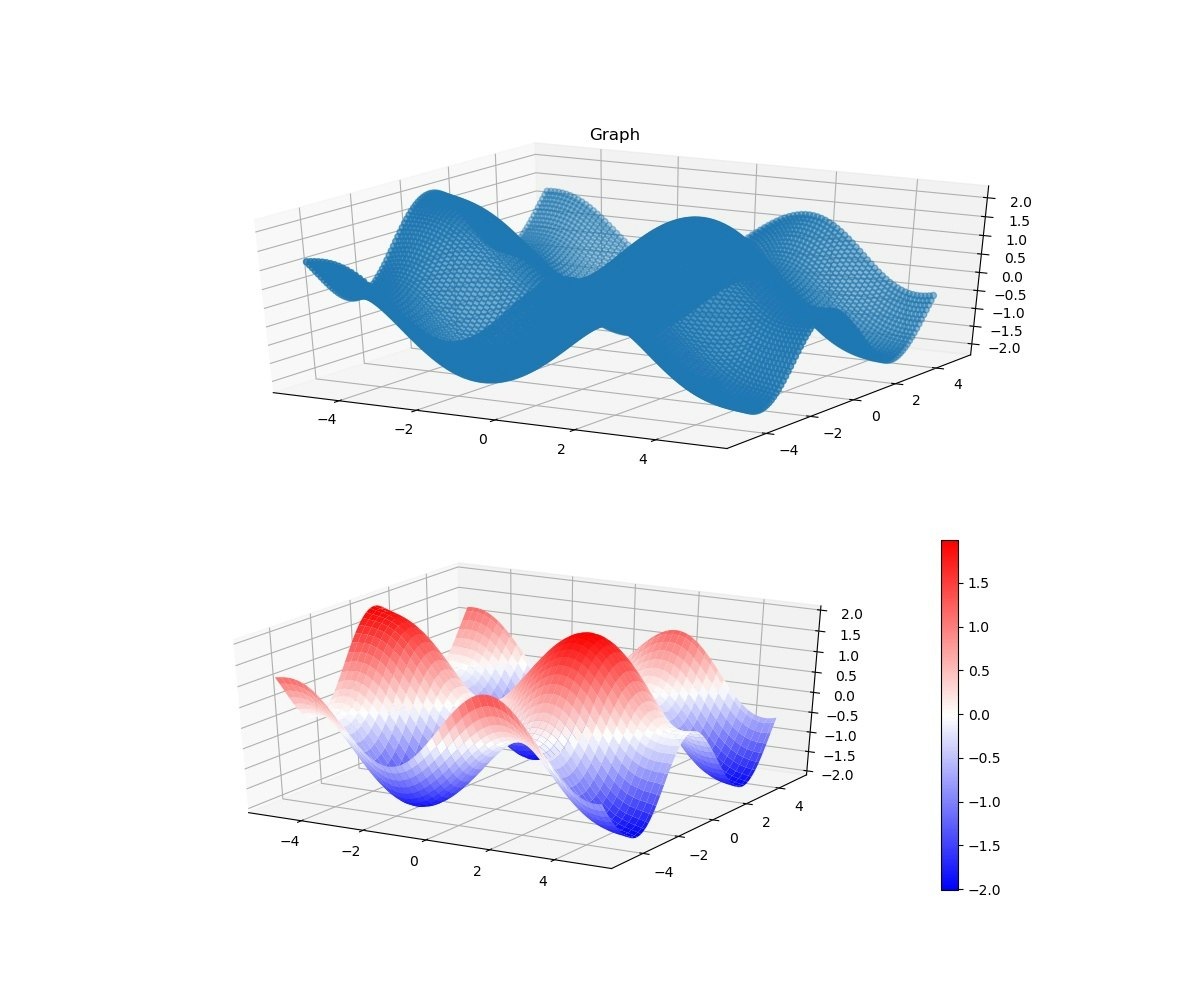
そして、RMSEと相関係数は以下のとおり、かなり一致している。
RBF: RMSE 0.053921 Corr 0.998494
まとめ
・SVMのちょっと理論をまとめた
・回帰を機械学習でやってみた
・多変量回帰をグラフで確認した
・現実的なデータに応用してみたくなった