以下の統計検定2級対策動画で用いられているスライドの一部です。
具体例から始めよう (1/6)
エンジニアのスキル調査
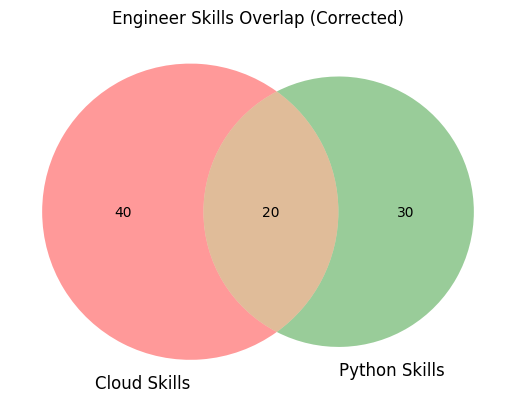
あるIT企業に勤務する 150人 のエンジニアに、スキル調査を行いました。
- クラウド技術の経験者: 60人
- Python開発の経験者: 50人
- 両方の経験者: 20人
問い: 無作為に1人を選んだとき、その人が 「クラウド技術の経験者」または「Python開発の経験者」 である確率は?
具体例から始めよう (2/6)
状況を視覚化する
このエンジニアのスキル保有状況は、ベン図で表現すると分かりやすくなります。
具体例から始めよう (3/6)
それぞれの事象の確率
まず、2つの事象を定義します。
- 事象A: 選ばれた人が クラウド技術 の経験者である
- 事象B: 選ばれた人が Python の開発経験者である
それぞれの確率は、以下のようになります。
- 事象A が起こる確率: $P(A) = \frac{60}{150} = \frac{2}{5}$
- 事象B が起こる確率: $P(B) = \frac{50}{150} = \frac{1}{3}$
具体例から始めよう (4/6)
重複に注意!
単純に $P(A)$ と $P(B)$ を足すとどうなるでしょうか?
- $P(A) + P(B)$ を計算すると、「クラウドとPythonの両方の経験者」 20人 を 2回 数えてしまいます。
この 「事象Aと事象Bが同時に起こる」 事象を 積事象 と呼びます。
- 積事象 の確率: $P(A \cap B) = \frac{20}{150} = \frac{2}{15}$
具体例から始めよう (5/6)
重複を引いて確率を求める
正しい確率を求めるには、重複して数えた 積事象の確率 を1回引く必要があります。
$$
P(A \cup B) = P(A) + P(B) - P(A \cap B)
$$
$$
\begin{aligned}
P(A \cup B) &= \frac{60}{150} + \frac{50}{150} - \frac{20}{150} \
&= \frac{90}{150} = \frac{3}{5}
\end{aligned}
$$
答え: 求める確率は $\frac{3}{5}$ (0.6) です。
もう一つの具体例 (1/3)
製品倉庫のピッキング
次に、重複がないケースを見てみましょう。
ある倉庫に、3種類の製品が保管されています。
- 製品A: 45%
- 製品B: 35%
- 製品C: 20%
問い: 無作為に1つの製品を取り出すとき、それが 「製品A」または「製品C」 である確率は?
もう一つの具体例 (2/3)
同時に起こりえない事象 (排反)
この例では、1つの製品が 同時に「製品A」であり、かつ「製品C」である ことはありません。
このように、2つの事象が 同時に起こりえない 関係にあるとき、
これらの事象は互いに 排反 であると言います。
-
排反 の場合、先ほどのような 重複 (積事象) は存在しません 。
($P(A \cap C) = 0$)
もう一つの具体例 (3/3)
単純な足し算で計算
事象が互いに 排反 なので、確率は単純な足し算で求められます。
- 事象X: 製品がAである確率 $P(X) = 0.45$
- 事象Y: 製品がCである確率 $P(Y) = 0.20$
$$
\begin{aligned}
P(X \cup Y) &= P(X) + P(Y) \
&= 0.45 + 0.20 \
&= 0.65
\end{aligned}
$$
答え: 求める確率は 0.65 です。
まとめ:概念の一般化
確率の基本用語
これまでの具体例を踏まえ、用語を整理しましょう。
-
事象
試行によって起こりうる個々の結果。 -
和事象 ($A \cup B$)
事象A または 事象Bの 少なくとも一方が起こる 事象。 -
積事象 ($A \cap B$)
事象Aと事象Bが 同時に起こる 事象。 -
排反事象
2つの事象が 同時に起こりえない 関係。($P(A \cap B) = 0$)
まとめ:加法定理の公式
1. 一般的な加法定理
2つの事象の 和事象 の確率を求めるための公式が 加法定理 です。
$$
P(A \cup B) = P(A) + P(B) - P(A \cap B)
$$
ポイント:
$P(A)$ と $P(B)$ の和から、重複して数えた 積事象の確率 $P(A \cap B)$ を引きます。
(エンジニアのスキルの例)
まとめ:加法定理の公式
2. 事象が排反の場合
2つの事象が互いに 排反 である場合、積事象の確率は $P(A \cap B) = 0$ となります。
そのため、公式はより単純になります。
$$
P(A \cup B) = P(A) + P(B)
$$
ポイント:
重複がないため、それぞれの事象の確率を 単純に足し合わせるだけ です。
(製品倉庫の例)
本日のまとめ
-
重複がある場合 (一般)
$P(A \cup B) = P(A) + P(B) - P(A \cap B)$ -
重複がない場合 (排反)
$P(A \cup B) = P(A) + P(B)$
事象間に重複があるか (排反でないか) を見極めることが重要です!