以下の統計検定2級対策動画で用いられているスライドの一部です。
具体例から学ぶ標準偏差
ケース1:集団内での自分の位置を知る
あるプログラミング能力試験を受けました。
自分の成績が、 受験者全体の中でどのくらいのレベルなのか を客観的に知りたい…
このような場合、 標準偏差 を使うことで、集団内での相対的な位置を正確に評価できます。
【例題1】 プログラミング能力試験
ある受験者Aさんの状況は以下の通りです。
この成績は、集団の中でどの程度の位置にあると言えるでしょうか?
| 項目 | 値 |
|---|---|
| Aさんの得点 | 83点 |
| 受験者全体の平均点 | 65点 |
| 受験者全体の標準偏差 | 12点 |
解答ステップ①:平均からの距離を測る
まず、Aさんの得点が平均点からどれだけ離れているかを、 標準偏差を「ものさし」として 測ります。
- Aさんと平均点の差: $83点 - 65点 = 18点$
- 標準偏差(12点)で割る: $18点 \div 12点 = 1.5$
これは、Aさんの得点が 「平均点から標準偏差1.5個分だけ高い位置」 にあることを意味します。
解答ステップ②:「偏差値」に変換する
次に、この「1.5」という値を、私たちがよく知る 偏差値 (平均50, 標準偏差10の尺度)に変換します。
$$
1.5 \times 10 + 50 = 65
$$
- Aさんの偏差値は 65 となります。
- 偏差値の平均は50なので、65というスコアは かなり優秀な成績 であることが客観的にわかります。
【例題1のまとめ】
- 標準偏差は、集団内での 相対的な位置を測る「ものさし」 として機能します。
- 異なるテストの結果でも、偏差値に変換することで 同じ土俵で比較 することが可能になります。
具体例から学ぶ標準偏差
ケース2:データが発生する範囲を予測する
ある工場でボルトを製造しています。
製品の品質は安定しているか?
規格外の製品はどのくらいの確率で発生するのか を予測したい…
このような場合も、 標準偏差 と 正規分布 を組み合わせることで、データの発生範囲を予測できます。
【例題2】 ボルトの品質管理
ある工場で製造されるボルトの長さは、以下の特性を持つ正規分布に従うことがわかっています。
| 項目 | 値 |
|---|---|
| 平均の長さ | 50.0 mm |
| 長さの標準偏差 | 0.2 mm |
【例題2】 問い
このとき、以下の問いに答えてください。
-
製造されたボルトのうち、長さが 49.8 mm から 50.2 mm の範囲に含まれるものは、全体の約何%ですか?
-
長さが 50.4 mm 以上 になるものは、全体の約何%ですか?
解説の鍵:正規分布と「68-95-99.7ルール」
多くの統計データは、平均値を中心とした左右対称の釣鐘型である 正規分布 に従います。正規分布には、標準偏差を使って、データが含まれる範囲を予測できる、という便利な性質があります。
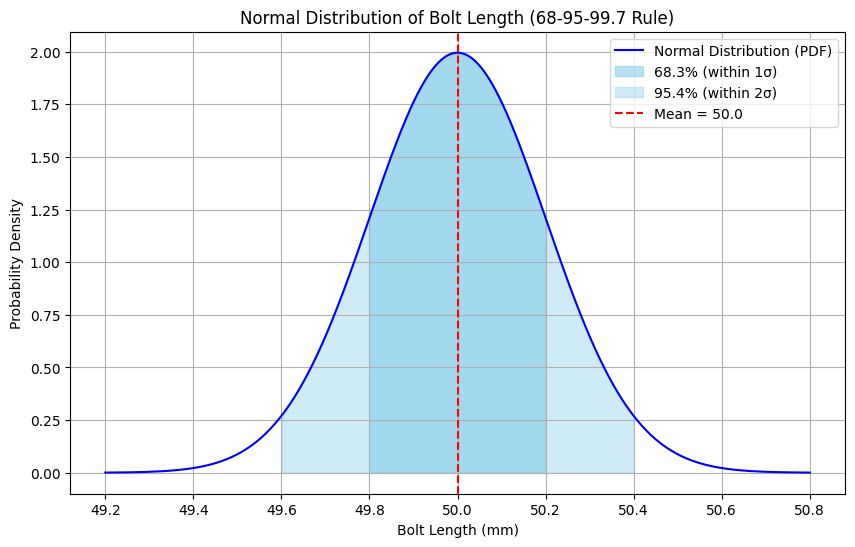
- 平均 ± 1 標準偏差 の範囲に、全体の約 68.3% が含まれる
- 平均 ± 2 標準偏差 の範囲に、全体の約 95.4% が含まれる
- 平均 ± 3 標準偏差 の範囲に、全体の約 99.7% が含まれる
正規分布の可視化
解答1:長さ 49.8 mm ~ 50.2 mm の割合
まず、この範囲が平均からどれだけ離れているかを確認します。
- 49.8 mm = 50.0 mm (平均) - 0.2 mm ( 1 × 標準偏差)
- 50.2 mm = 50.0 mm (平均) + 0.2 mm ( 1 × 標準偏差)
これは、「平均 ± 1 標準偏差」の範囲に該当します。
「68-95-99.7ルール」から、この範囲には全体の約 68.3% が含まれます。
解答2:長さ 50.4 mm 以上の割合
-
基準となる範囲を確認
- 50.4 mm は「平均 + 2 × 標準偏差」の点です。
- ルールより、「平均 ± 2 標準偏差」(49.6 mm ~ 50.4 mm)の範囲に 95.4% が含まれます。
-
範囲外の割合を計算
- この範囲から外れるデータは $100% - 95.4% = 4.6%$ です。
-
片側の割合を計算
- 正規分布は左右対称なので、上限側(50.4 mm以上)の割合はその半分です。
- $4.6% \div 2 = 2.3%$
よって、答えは全体の約 2.3% です。
具体例から学ぶ標準偏差
ケース3:データのばらつきを比較する
2つのECサイトを運営しています。
どちらのサイトの注文件数が、 日によってより安定的か を評価したい…
これは、標準偏差の最も基本的な使い方です。
標準偏差の大小を直接比較する ことで、データのばらつきを評価できます。
【例題3】 2つのECサイトの比較
過去1ヶ月間の1日あたりの注文件数を集計した結果は以下の通りです。
どちらのサイトの注文件数が、日によってより安定的(ばらつきが小さい)と言えるでしょうか?
| サイトA | サイトB | |
|---|---|---|
| 平均注文件数 | 200件 | 220件 |
| 標準偏差 | 15件 | 40件 |
解答:標準偏差を比較するだけ
- サイトAの標準偏差: 15件
- サイトBの標準偏差: 40件
サイトAの標準偏差は、サイトBよりも小さいです。
結論:サイトA の方が、日々の注文件数のばらつきが小さく、より安定的である。
- サイトBは平均注文件数こそ多いものの、日による変動が非常に大きいことがわかります。この分析は売上予測や在庫管理に役立ちます。
ここまでのまとめ:具体例から見えたこと
ここまで3つの具体例を見てきました。
これらの例を踏まえ、標準偏差の役割を一般化して定義し直してみましょう。
- 偏差値の計算
- データ発生範囲の予測
- データセットの比較
標準偏差は、これら全てを可能にする強力なツールです。
【一般化と定義 1/3】 標準偏差とは?
データの 「ばらつき具合」 を表す数値
-
標準偏差が小さい
- データが平均値の周りに 密集している
- 値が 安定的 である
-
標準偏差が大きい
- データが平均値から 広範囲に散らばっている
- 値の 変動が大きい
【一般化と定義 2/3】 偏差値の公式
集団内での個人の相対的な位置を比較するため、平均が50、標準偏差が10の尺度に変換したものが「偏差値」です。
$$
偏差値 = \frac{個人の得点 - 平均点}{標準偏差} \times 10 + 50
$$
- この式により、平均点やデータ数が異なる集団同士でも、 同じ土俵で値を比較 できます。
【一般化と定義 3/3】 正規分布の「68-95-99.7ルール」
データが正規分布に従う場合、標準偏差を用いてデータが発生する確率を予測できます。
- 平均 ± 1標準偏差 の範囲に、約 68.3% が含まれる
- 平均 ± 2標準偏差 の範囲に、約 95.4% が含まれる
- 平均 ± 3標準偏差 の範囲に、約 99.7% が含まれる