以下の統計検定2級対策動画で用いられているスライドの一部です。
こんな確率、計算できますか?
2つの異なる状況を例に、連続して起こる確率の計算方法を見ていきましょう。
例題1:互いに影響し合わない事象
- 例題1: 2つの工場の製品が 両方とも良品 である確率
例題2:互いに影響し合う事象
- 例題2: くじ引きで 1人目に男性、2人目に女性 が選ばれる確率
例題1:互いに影響し合わない事象
ある工場に、完全に独立して稼働する2つの生産ラインXとYがあります。
- ラインXの製品が規格内である確率: 95%
- ラインYの製品が規格内である確率: 98%
問: ラインXとYから製品を1つずつ抜き出した際、 両方とも規格内である確率 は?
例題1:考え方
この問題では、2つの事象を考えます。
- 事象A: ラインXの製品が規格内である
- 事象B: ラインYの製品が規格内である
ポイント
一方の事象(ラインXの結果)が、もう一方の事象(ラインYの結果)の確率に 一切影響を与えません。
このような関係にある事象を「 独立な事象 」と呼びます。
例題1:計算と結論
独立な事象の確率は、それぞれの確率を単純に掛け合わせることで計算できます。
- 事象Aの確率 $P(A) = 0.95$
- 事象Bの確率 $P(B) = 0.98$
両方が同時に起こる確率 $P(A \cap B)$ は…
$$
P(A \cap B) = 0.95 \times 0.98 = 0.931
$$
結論: 両方の製品が規格内である確率は 93.1% です。
例題2:互いに影響し合う事象
ある部署に10人(男性6人、女性4人)が所属しています。
この中からプレゼンターを2人、順番にくじ引きで選びます。
(一度引いたくじは元に戻しません)
問: 1人目に男性 が選ばれ、かつ 2人目に女性 が選ばれる確率は?
例題2:考え方
この問題でも、2つの事象を考えます。
- 事象A: 1人目に男性が選ばれる
- 事象B: 2人目に女性が選ばれる
ポイント
1人目のくじ引きの結果によって、2人目のくじを引く際の状況(人数構成)が 変化します。
このように、一方の事象がもう一方の確率に影響を与える関係を「 従属な事象 」と呼びます。
例題2:計算ステップ①
従属な事象の確率は、段階的に考えます。
ステップ1: 1人目に男性が選ばれる確率 $P(A)$ を求める
- 全体:10人
- 男性:6人
したがって、1人目に男性が選ばれる確率は次のようになります。
$$
P(A) = \frac{6}{10}
$$
例題2:計算ステップ②
ステップ2:「1人目に男性が選ばれた後で」2人目に女性が選ばれる確率を求める
この「〜という条件のもとで」の確率を「 条件付き確率 」と呼び、 $P(B|A)$ と表記します。
- 残りの人数:9人
- 残りの女性:4人
したがって、条件付き確率は次のようになります。
$$
P(B|A) = \frac{4}{9}
$$
例題2:計算と結論
最後に、ステップ1とステップ2の確率を掛け合わせることで、連続して起こる確率 $P(A \cap B)$ が求まります。
$$
P(A \cap B) = P(A) \times P(B|A)
$$
$$
= \frac{6}{10} \times \frac{4}{9} = \frac{24}{90} = \frac{4}{15}
$$
結論: 1人目に男性、2人目に女性が選ばれる確率は $\frac{4}{15}$ (約26.7%)です。
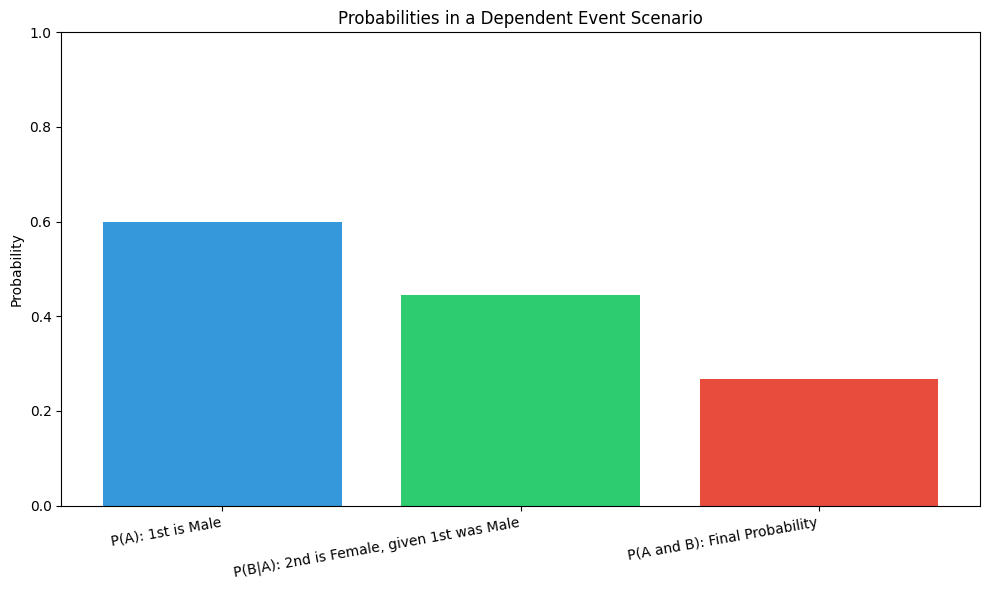
例題2の確率を可視化する
各ステップの確率をグラフで見てみましょう。
import matplotlib.pyplot as plt
# Data
labels = ['P(A): 1st is Male', 'P(B|A): 2nd is Female, given 1st was Male', 'P(A and B): Final Probability']
probabilities = [6/10, 4/9, 4/15]
# Plot
fig, ax = plt.subplots(figsize=(10, 6))
bars = ax.bar(labels, probabilities, color=['#3498db', '#2ecc71', '#e74c3c'])
# Add labels and title
ax.set_ylabel('Probability')
ax.set_title('Probabilities in a Dependent Event Scenario')
ax.set_ylim(0, 1)
# Add text on bars
for bar in bars:
yval = bar.get_height()
ax.text(bar.get_x() + bar.get_width()/2.0, yval, f'{yval:.3f}', ha='center', va='bottom', fontsize=12, color='white', weight='bold')
plt.xticks(rotation=10, ha="right")
plt.tight_layout()
plt.show()
一般化と定義
ここまでの具体例を踏まえて、法則を一般化します。
2つ以上の事象が同時に(または連続して)起こる確率、すなわち 積事象 の確率を計算するための法則。
それが「 確率の乗法定理 」です。
乗法定理の基本形(従属な場合)
事象AとBが両方とも起こる確率 $P(A \cap B)$ は、以下の式で表されます。
$$
P(A \cap B) = P(A) \times P(B|A)
$$
- $P(A)$ : 事象Aが起こる確率
- $P(B|A)$ : 事象Aが起こったという 条件のもとで 、事象Bが起こる確率( 条件付き確率 )
これは、例題2のような 従属な事象 の場合に使う基本の形です。
乗法定理の応用形(独立な場合)
事象AとBが 独立 の場合、Aの結果はBの確率に影響しません。
したがって、条件付き確率 $P(B|A)$ は、単にBが起こる確率 $P(B)$ と同じになります。
$$
P(B|A) = P(B)
$$
これを基本形に代入すると、 独立な事象 のためのシンプルな公式が得られます。
$$
P(A \cap B) = P(A) \times P(B)
$$
まとめ
- 乗法定理 は、複数の事象が同時に起こる確率 $P(A \cap B)$ を求めるための法則です。
- 計算する際は、事象が 独立 か 従属 かを見極めることが最も重要です。
| 事象の関係 | 公式 | 計算方法 |
|---|---|---|
| 独立 | $P(A \cap B) = P(A) \times P(B)$ | 単純な掛け算 |
| 従属 | $P(A \cap B) = P(A) \times P(B|A)$ | 条件付き確率を掛ける |