以下の統計検定2級対策動画で用いられているスライドの一部です。
はじめに
このスライドでは、統計学の重要な概念である「 期待値 」について解説します。
- 期待値って、結局なに?
- 具体的にどうやって計算するの?
という疑問に、2つの具体例を通して答えていきます。
まずは、身近な くじ引きの例 から見ていきましょう。
【具体例①】くじ引きの期待値
あるイベントで、1回 300円 で引けるくじがあります。
賞金と確率は以下の通りです。
| 等 | 賞金額 (円) | 当選確率 |
|---|---|---|
| 1等 | 10,000 | 1/200 |
| 2等 | 1,000 | 10/200 |
| 3等 | 300 | 50/200 |
| ハズレ | 0 | 139/200 |
このくじを1回引いたとき、 平均的にいくらの賞金がもらえる でしょうか?
平均的な賞金額を計算してみよう
各賞金に対して、それが当たる確率を掛け合わせます。
- 1等: $10000 \times \frac{1}{200} = 50$ 円
- 2等: $1000 \times \frac{10}{200} = 50$ 円
- 3等: $300 \times \frac{50}{200} = 75$ 円
- ハズレ: $0 \times \frac{139}{200} = 0$ 円
計算結果の合計
先ほど計算した値をすべて足し合わせます。
$$
50 + 50 + 75 + 0 = 175
$$
この 175円 が、このくじから得られる賞金額の 期待値 です。
期待値とは、試行を無数に繰り返した場合に得られる結果の 平均値 のことです。
このくじは参加費300円なので、平均的に 125円 損をすると考えられます。
一般化:離散型確率変数の期待値
くじの賞金のように、 とびとびの値 をとる変数を 離散型確率変数 と呼びます。
この期待値 $E(X)$ は、確率変数 $X$ がとる値 $x_i$ と、その値をとる確率 $P(X=x_i)$ を使って、以下のように一般化されます。
(値)と(その値をとる確率)を掛けて、 すべて足し合わせる(総和)
$$
E(X) = \sum_{i} x_i P(X=x_i)
$$
【具体例②】バスの待ち時間の期待値
次に、少し違うタイプの例を見てみましょう。
あるバス停では、バスは 0分後から12分後 の間に ランダムに やってきます。
このとき、平均的な待ち時間は何分でしょうか?
この「待ち時間」は、0分から12分の間の 連続的な値 をとります。
連続的な値の確率分布
待ち時間のように連続的な値をとる変数を 連続型確率変数 と呼びます。
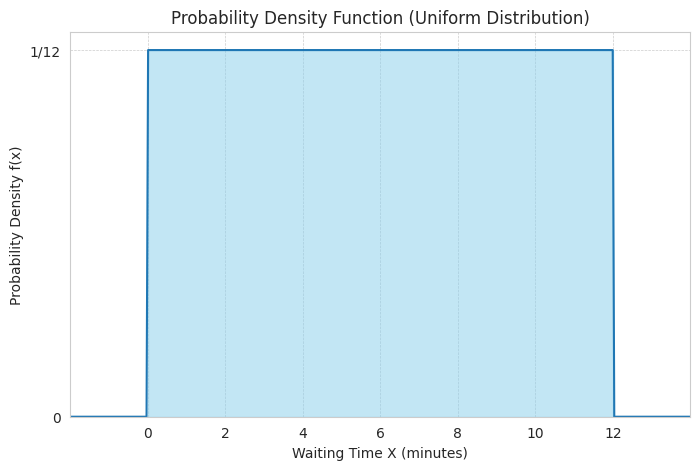
今回の例では、0分から12分の間で到着する確からしさは一定です。
この確率の分布をグラフで表すと、以下のようになります。
このグラフで示される関数を 確率密度関数 と呼びます。
確率密度関数の描画コード (Python)
import matplotlib.pyplot as plt
import numpy as np
# Data for plotting
x = np.linspace(-2, 14, 400)
y = np.where((x >= 0) & (x <= 12), 1/12, 0)
# Create the plot
fig, ax = plt.subplots(figsize=(8, 5))
ax.plot(x, y, label='f(x)')
ax.fill_between(x, y, where=((x >= 0) & (x <= 12)), color='skyblue', alpha=0.5)
# Set titles and labels
ax.set_title('Probability Density Function (Uniform Distribution)')
ax.set_xlabel('Waiting Time X (minutes)')
ax.set_ylabel('Probability Density f(x)')
ax.set_xticks(np.arange(0, 13, 2))
ax.set_yticks([0, 1/12])
ax.set_yticklabels(['0', '1/12'])
ax.grid(True, which='both', linestyle='--', linewidth=0.5)
ax.set_ylim(bottom=0)
ax.set_xlim(-2, 14)
# Show the plot
plt.show()
待ち時間の期待値を計算する
連続型の場合、離散型の「総和 $\sum$」の代わりに「 積分 $\int$ 」を使って期待値を計算します。
確率密度関数は $f(x) = \frac{1}{12}$ (ただし $0 \le x \le 12$)なので、
$$
\begin{aligned}
E(X) &= \int_{0}^{12} x \cdot f(x) dx \
&= \int_{0}^{12} x \cdot \frac{1}{12} dx \
&= \frac{1}{12} \left[ \frac{1}{2}x^2 \right]_{0}^{12} \
&= \frac{1}{12} \left( \frac{144}{2} - 0 \right) = 6
\end{aligned}
$$
待ち時間の期待値は 6分 であることが分かりました。
一般化:連続型確率変数の期待値
バスの待ち時間のように、 連続的な値 をとる変数を 連続型確率変数 と呼びます。
この期待値 $E(X)$ は、確率密度関数 $f(x)$ を使って、以下のように一般化されます。
(値)と(確率密度関数)を掛けて、定義域全体で積分する
$$
E(X) = \int_{-\infty}^{\infty} x f(x) dx
$$
期待値の便利な性質
期待値には、計算に役立ついくつかの基本的な性質があります。
($X, Y$は確率変数、 $c$は定数)
- 定数の期待値: $E(c) = c$
- 定数との和: $E(X + c) = E(X) + c$
- 定数倍: $E(cX) = cE(X)$
- 和の期待値: $E(X + Y) = E(X) + E(Y)$
まとめ
- 期待値 とは、確率的な現象における結果の 平均値
-
離散型 の場合
- (値) × (確率) の 総和 $\sum$ で計算
$$ E(X) = \sum_{i} x_i P(X=x_i) $$
- (値) × (確率) の 総和 $\sum$ で計算
-
連続型 の場合
- (値) × (確率密度) の 積分 $\int$ で計算
$$ E(X) = \int_{-\infty}^{\infty} x f(x) dx $$
- (値) × (確率密度) の 積分 $\int$ で計算