以下の統計検定2級対策動画で用いられているスライドの一部です。
今回のテーマ
あるIT企業の従業員データを使って、以下の疑問に答えていきます。
- 「従業員が エンジニアだった とき、その人が Macを使っている 確率は?」
- 「 エンジニアであること 」と「 Macを使っていること 」は、お互いに関係があるのか?
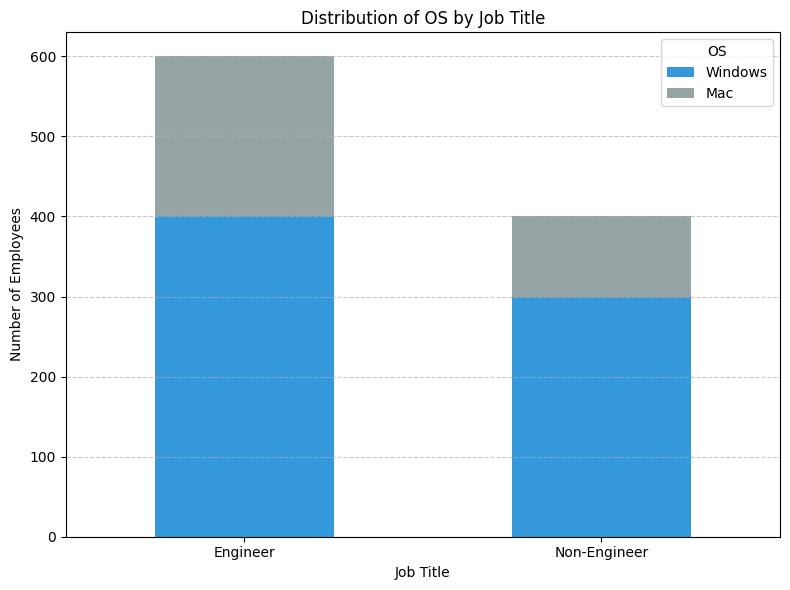
具体例:あるIT企業の従業員データ
従業員1000人を対象に、職種と使用OSを調査しました。
| エンジニア | 非エンジニア | 合計 | |
|---|---|---|---|
| Windows | 400 | 300 | 700 |
| Mac | 200 | 100 | 300 |
| 合計 | 600 | 400 | 1000 |
グラフの描画コード (Python)
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# Create DataFrame
data = {
'Engineer': [400, 200],
'Non-Engineer': [300, 100]
}
index = ['Windows', 'Mac']
df = pd.DataFrame(data, index=index)
# Plotting a stacked bar chart
df_transposed = df.T
df_transposed.plot(kind='bar', stacked=True, figsize=(8, 6), color=['#3498db', '#95a5a6'])
plt.title('Distribution of OS by Job Title')
plt.xlabel('Job Title')
plt.ylabel('Number of Employees')
plt.xticks(rotation=0)
plt.legend(title='OS')
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()
問題 1
条件付き確率を考えてみよう
1000人の従業員から無作為に1人を選びます。
その従業員が エンジニアであったとき 、その人が Macを使用している 確率はいくらでしょうか?
この「〜だった とき の確率」が、 条件付き確率 です。
考え方①:視点を絞り込む
エンジニアであった とき
この条件に注目し、考える範囲を エンジニアの集団(600人) に限定します。
その人がMacを使用している確率は?
エンジニア600人の中で、Macを使用しているのは200人です。
その割合を計算すると…
$$
\frac{200}{600} = \frac{1}{3} \approx 33.3%
$$
考え方②:確率の割り算で計算する
事象を以下のように定義します。
- 事象A: Macを使用している
- 事象B: エンジニアである
1. 各確率を計算
- エンジニアである確率 $P(B) = \frac{600}{1000} = 0.6$
- Macを使うエンジニアである確率 $P(A \cap B) = \frac{200}{1000} = 0.2$
2. 確率を割り算する
「エンジニアである」という世界の中で、「Macを使うエンジニア」が占める割合を計算します。
$$
\frac{P(A \cap B)}{P(B)} = \frac{0.2}{0.6} = \frac{1}{3}
$$
一般化:条件付き確率とは?
ここまでの話を一般化します。
条件付き確率 とは、ある事象Bが起こったという条件の下で、別の事象Aが起こる確率のことです。
- 記号: $P(A|B)$
-
公式:
$$
P(A|B) = \frac{P(A \cap B)}{P(B)}
$$
これは、考察の範囲を 事象Bが起こった世界 に限定し、その中での事象Aの割合を見ていることを意味します。
問題 2
事象の独立を考えてみよう
「エンジニアである」という事象と、「Macを使用している」という事象は、 独立 でしょうか、それとも 従属 でしょうか?
- 独立: 2つの事象が互いに 無関係 であること。
- 従属: 2つの事象が互いに 何らかの関係がある こと。
考え方:確率を比較する
もし2つの事象が 独立 なら、片方の情報がもう片方の確率に影響しないはずです。
- 「Macを使っている」確率: $P(A)$
- 「エンジニアだった とき にMacを使っている」確率: $P(A|B)$
この2つが等しければ 独立 、異なれば 従属 と言えます。
実際に比較してみよう
-
$P(A|B)$ (エンジニアの条件でMacを使う確率):
- 先ほどの計算より、 $\frac{1}{3} \approx 0.333$
-
$P(A)$ (条件なしでMacを使う確率):
- 全従業員1000人中、Macユーザーは300人なので、
- $P(A) = \frac{300}{1000} = 0.3$
比較結果
$$
0.333 \neq 0.3
$$
2つの確率は異なるため、これらの事象は 独立ではなく、従属である ことが分かります。
便利な判定方法
独立性の判定には、より直接的な方法があります。
それは、以下の式が成り立つかどうかを調べることです。
$$
P(A \cap B) = P(A) \times P(B)
$$
左辺 (AかつBが起こる確率):
$P(A \cap B) = \frac{200}{1000} = 0.2$
右辺 (Aが起こる確率 × Bが起こる確率):
$P(A) \times P(B) = 0.3 \times 0.6 = 0.18$
$0.2 \neq 0.18$ なので、やはり 従属 であると結論付けられます。
一般化:事象の独立とは?
ここまでの話を一般化します。
事象の独立 とは、一方の事象が起こるかどうかが、もう一方の事象が起こる確率に一切影響を与えない関係性のことです。
以下の いずれか の式が成立する場合、事象AとBは 独立 です。
- $P(A|B) = P(A)$
- $P(B|A) = P(B)$
- $P(A \cap B) = P(A) \times P(B)$
式が成立しない場合、2つの事象は 従属 であると言います。
参考:乗法定理
条件付き確率の公式 $P(A|B) = \frac{P(A \cap B)}{P(B)}$ を変形すると、 乗法定理 と呼ばれる公式が得られます。
$$
P(A \cap B) = P(B) \times P(A|B)
$$
これは、事象Aと事象Bが 同時に起こる確率 を、条件付き確率を使って計算するための便利な公式です。
まとめ
-
条件付き確率 $P(A|B)$
- 事象Bが起こったという条件の下で、事象Aが起こる確率。
$$P(A|B) = \frac{P(A \cap B)}{P(B)}$$
- 事象Bが起こったという条件の下で、事象Aが起こる確率。
-
事象の独立
- 2つの事象が互いに影響を与えない関係。
$$P(A \cap B) = P(A) \times P(B)$$
- 2つの事象が互いに影響を与えない関係。