Go to Qiita Advent Calendar Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@Mrs_P

2つのグループの平均値の差を推定する_母平均の差の信頼区間_統計検定2級対策

Posted at

以下の統計検定2級対策動画で用いられているスライドの一部です。

このテーマが重要な理由

ビジネスや研究の現場では、次のような問いが頻繁に生じます。

「2つのグループの平均値に、本当に意味のある差はあるのか？」

  • A/Bテストで、新旧デザインのクリック率に差はあるか？
  • 2つの製造ラインで作られた製品の品質に差はあるか？

このような問いに統計的な根拠を持って答える手法が 「母平均の差の信頼区間」 の推定です。

このスライドの対象者

  • 標本と母集団、平均、分散といった基本的な統計用語を理解している方
  • 正規分布とt分布の基本的な特性について知識がある方
  • 2つのグループ間の差を統計的に評価したいと考えている方

母平均の差の信頼区間とは？

2つの独立した母集団から抽出した標本に基づき、 母平均の差 $\mu_1 - \mu_2$ が含まれると統計的に期待される 範囲 のことです。

例えば、「95%信頼区間」を算出した場合、その区間内に 真の母平均の差 が含まれると95%の確からしさで期待できます。

信頼区間から何がわかるか？

信頼区間を求めることで、主に2つの点を評価できます。

  1. 差の大きさ

    • 2つの母平均の差が、どの程度の範囲にあると推定されるか。

  2. 差の有無（これが最重要）

    • 信頼区間が 0 を含むかどうかが、判断の鍵となります。

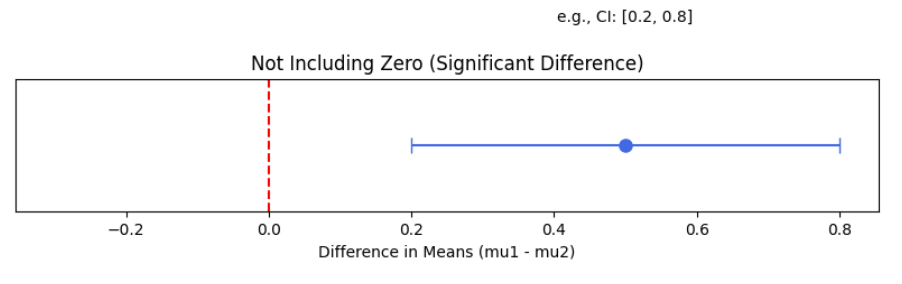
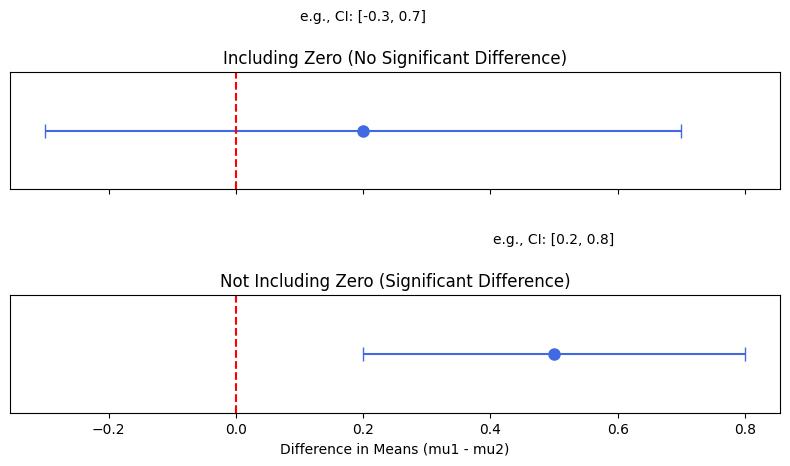
信頼区間の解釈：可視化イメージ

  • 差があるとは言えない場合

    • 信頼区間が 0 をまたぐ。
    • これは、母平均の差が 0 である可能性を否定できないことを意味します。

    image.png

  • 差があると言える場合

    • 信頼区間が 0 をまたがない。
    • これは、母平均に統計的に意味のある差が存在することを示唆します。

    image.png

信頼区間の解釈：可視化イメージ

image.png

import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.sans-serif'] = ['DejaVu Sans']

fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(8, 5), sharex=True)

# Case: Not Significant (Includes zero)
ax1.errorbar(0.2, 0, xerr=0.5, fmt='o', capsize=5, color='royalblue', markersize=8)
ax1.axvline(0, color='red', linestyle='--')
ax1.set_yticks([])
ax1.set_title('Including Zero (No Significant Difference)')
ax1.text(0.2, 0.1, 'e.g., CI: [-0.3, 0.7]', ha='center', va='bottom')

# Case: Significant (Does not include zero)
ax2.errorbar(0.5, 0, xerr=0.3, fmt='o', capsize=5, color='royalblue', markersize=8)
ax2.axvline(0, color='red', linestyle='--')
ax2.set_yticks([])
ax2.set_xlabel('Difference in Means (mu1 - mu2)')
ax2.set_title('Not Including Zero (Significant Difference)')
ax2.text(0.5, 0.1, 'e.g., CI: [0.2, 0.8]', ha='center', va='bottom')

plt.tight_layout()
plt.show()

算出方法の3つのケース

信頼区間の算出方法は、母集団の分散に関する情報によって、主に3つのケースに分類されます。

  1. 母分散が 既知 の場合

    • 標準正規分布 を使用

  2. 母分散が 未知だが等しい と仮定できる場合

    • t分布 を使用

  3. 母分散が 未知で等しいと仮定できない 場合

    • t分布 を使用（ Welchの方法 ）

Case 1: 母分散が既知の場合

Case 1: 具体例

ある製薬会社が2種類の睡眠導入剤（A薬, B薬）の効果を比較しています。過去のデータから母分散は分かっています。

  • A薬
    • 標本サイズ $n_1=100$
    • 標本平均 $\bar{x}_1=2.5$ 時間
    • 母分散 $\sigma_1^2=1.21$
  • B薬
    • 標本サイズ $n_2=120$
    • 標本平均 $\bar{x}_2=2.1$ 時間
    • 母分散 $\sigma_2^2=1.44$

課題: 母平均の差 $\mu_1 - \mu_2$ に対する 95%信頼区間 を求める。

Case 1: 計算手順

  1. 標本平均の差
    • $\bar{x}_1 - \bar{x}_2 = 2.5 - 2.1 = 0.4$
  2. 標準誤差の計算
    • $\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}} = \sqrt{\frac{1.21}{100} + \frac{1.44}{120}} \approx 0.1552$
  3. 信頼区間の算出
    • 95%信頼区間の場合、z値は1.96
    • $0.4 \pm 1.96 \times 0.1552$

計算すると、信頼区間は [0.0958, 0.7042] となります。

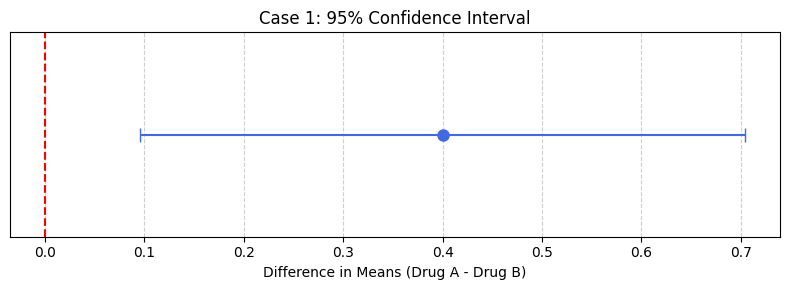
Case 1: 結果の解釈

算出された95%信頼区間は [0.0958, 0.7042] です。

  • この区間は 0 を含んでいません。
  • したがって、A薬の睡眠時間延長効果は、B薬よりも 統計的に有意に大きい と結論付けられます。

image.png

import matplotlib.pyplot as plt

plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.sans-serif'] = ['DejaVu Sans']

fig, ax = plt.subplots(figsize=(8, 3))
ax.errorbar(0.4, 0, xerr=(0.7042 - 0.0958)/2, fmt='o', capsize=5, color='royalblue', markersize=8)
ax.axvline(0, color='red', linestyle='--')
ax.set_yticks([])
ax.set_xlabel('Difference in Means (Drug A - Drug B)')
ax.set_title('Case 1: 95% Confidence Interval')
ax.grid(axis='x', linestyle='--', alpha=0.6)
plt.tight_layout()
plt.show()

Case 1: 一般化と公式

前提条件

  • 2つの母集団はそれぞれ正規分布に従う。
  • 2つの母分散 $\sigma_1^2$ と $\sigma_2^2$ の値が分かっている。

補足: この例のようにサンプルサイズが十分に大きい場合（目安: 各30以上）、中心極限定理により、たとえ母集団が厳密な正規分布でなくても、この方法は近似的に有効となります。

信頼区間の公式

信頼係数を $1-\alpha$ とすると、母平均の差の信頼区間は以下の式で計算されます。

$$
(\bar{x}_1 - \bar{x}2) \pm z{\alpha/2} \sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}
$$

  • $z_{\alpha/2}$ は標準正規分布の上側 $\alpha/2$ パーセント点です。

Case 2: 母分散が未知だが等しいと仮定できる場合

Case 2: 具体例

ある食品メーカーが2つのレシピ（X, Y）で作ったクッキーの糖度を比較しています。母分散は不明ですが、等しいと仮定します。また、母集団（各レシピの糖度）は正規分布に従うとします。

  • レシピX
    • $n_1=10$, $\bar{x}_1=15.2$, $s_1^2=1.8$
  • レシピY
    • $n_2=12$, $\bar{x}_2=14.1$, $s_2^2=2.1$

課題: 糖度の母平均の差 $\mu_1 - \mu_2$ に対する 95%信頼区間 を求める。

Case 2: 計算手順

母分散が未知のため、 プールされた分散 $s^2$ を計算し、 t分布 を用います。

  1. プールされた分散 $s^2$ の計算
    • $s^2 = \frac{(10-1) \times 1.8 + (12-1) \times 2.1}{10+12-2} = 1.965$
  2. 自由度とt値の確認
    • 自由度 $df = 10+12-2=20$
    • 自由度20の95%信頼区間のt値は $t_{0.025}(20) = 2.086$
  3. 信頼区間の算出
    • $(15.2 - 14.1) \pm 2.086 \sqrt{1.965(\frac{1}{10} + \frac{1}{12})}$

計算すると、信頼区間は [-0.152, 2.352] となります。

Case 2: 結果の解釈

算出された95%信頼区間は [-0.152, 2.352] です。

  • この区間は 0 をまたいでいます。
  • したがって、このデータからは、2つのレシピの糖度に 統計的に有意な差があるとは言えません 。

image.png

import matplotlib.pyplot as plt

plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.sans-serif'] = ['DejaVu Sans']

fig, ax = plt.subplots(figsize=(8, 3))
ax.errorbar(1.1, 0, xerr=(2.352 - (-0.152))/2, fmt='o', capsize=5, color='royalblue', markersize=8)
ax.axvline(0, color='red', linestyle='--')
ax.set_yticks([])
ax.set_xlabel('Difference in Means (Recipe X - Recipe Y)')
ax.set_title('Case 2: 95% Confidence Interval')
ax.grid(axis='x', linestyle='--', alpha=0.6)
plt.tight_layout()
plt.show()

Case 2: 一般化と公式

前提条件

  • 2つの母集団はそれぞれ正規分布に従う。
  • 2つの母分散は未知だが、等しいと仮定できる。

信頼区間の公式

まず、プールされた分散 $s^2$ を計算します。
$$
s^2 = \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2}
$$
この $s^2$ を使い、信頼区間を求めます。
$$
(\bar{x}_1 - \bar{x}2) \pm t{\alpha/2}(n_1+n_2-2) \sqrt{s^2(\frac{1}{n_1} + \frac{1}{n_2})}
$$

注: 今回の例のようにサンプルサイズが小さい場合、「母集団が正規分布に従う」という前提が特に重要になります。

Case 3: 母分散が未知で等しいと仮定できない場合

(Welchの方法)

Case 3: 具体例

新型エンジンと旧型エンジンの燃費性能を比較します。母分散は未知で、等しいという保証もありません。また、それぞれのエンジンの燃費の分布は正規分布に従うとします。

  • 新型エンジン
    • $n_1=18$, $\bar{x}_1=22.5$ km/L, $s_1^2=2.5$
  • 旧型エンジン
    • $n_2=15$, $\bar{x}_2=20.8$ km/L, $s_2^2=4.8$

課題: 燃費の母平均の差 $\mu_1 - \mu_2$ に対する 99%信頼区間 を求める。

Case 3: 計算手順

Welchの方法 では、特別な式で自由度 $\nu$ を計算します。

  1. 自由度 $\nu$ の計算 (Welch-Satterthwaiteの式)
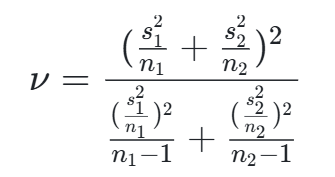
    image.png

    • 上記の複雑な計算の結果、$\nu \approx 24.95$ となります。
    • ここでは切り捨てて、自由度を 24 として扱います。

  2. t値の確認

    • 自由度24の99%信頼区間のt値は $t_{0.005}(24) = 2.797$

  3. 信頼区間の算出

    • $(22.5 - 20.8) \pm 2.797 \sqrt{\frac{2.5}{18} + \frac{4.8}{15}}$

計算すると、信頼区間は [-0.1947, 3.5947] となります。

Case 3: 計算手順

Welchの方法 では、特別な式で自由度 $\nu$ を計算します。

  1. 自由度 $\nu$ の計算 (Welch-Satterthwaiteの式)

    • 以下の式に値を代入して計算します。
      $$
      \nu = \frac{(\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2})^2}{\frac{(\frac{s_1^2}{n_1})^2}{n_1-1} + \frac{(\frac{s_2^2}{n_2})^2}{n_2-1}}
      $$
    • 計算すると、$\nu\approx 24.95$ となります。ここでは計算結果を切り捨て、自由度を 24 として扱います。

  2. t値の確認

    • 自由度24の99%信頼区間のt値は $t_{0.005}(24) = 2.797$

  3. 信頼区間の算出

    • $(22.5 - 20.8) \pm 2.797 \sqrt{\frac{2.5}{18} + \frac{4.8}{15}}$

計算すると、信頼区間は [-0.1947, 3.5947] となります。

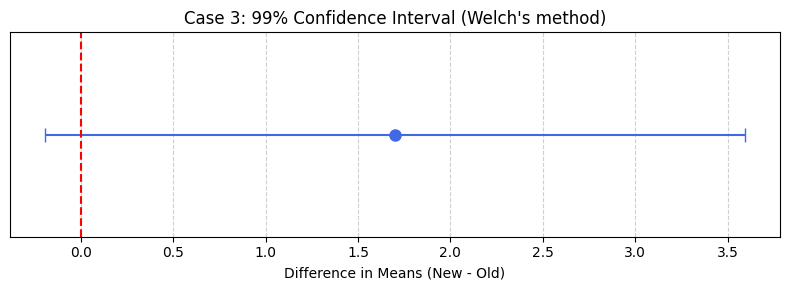
Case 3: 結果の解釈

算出された99%信頼区間は [-0.1947, 3.5947] です。

  • この区間は 0 をまたいでいます。
  • したがって、信頼係数99%という厳しい基準では、両エンジンの燃費に 統計的に有意な差があるとは断定できません 。

image.png

import matplotlib.pyplot as plt

plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.sans-serif'] = ['DejaVu Sans']

fig, ax = plt.subplots(figsize=(8, 3))
ax.errorbar(1.7, 0, xerr=(3.5947 - (-0.1947))/2, fmt='o', capsize=5, color='royalblue', markersize=8)
ax.axvline(0, color='red', linestyle='--')
ax.set_yticks([])
ax.set_xlabel('Difference in Means (New - Old)')
ax.set_title('Case 3: 99% Confidence Interval (Welch\'s method)')
ax.grid(axis='x', linestyle='--', alpha=0.6)
plt.tight_layout()
plt.show()

Case 3: 一般化と公式

前提条件

  • 2つの母集団はそれぞれ正規分布に従う。
  • 2つの母分散は未知であり、等しいと仮定することもできない。

信頼区間の公式

まず、自由度 $\nu$ を計算します。
$$
\nu = \frac{(\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2})^2}{\frac{(\frac{s_1^2}{n_1})^2}{n_1-1} + \frac{(\frac{s_2^2}{n_2})^2}{n_2-1}}
$$
この $\nu$ を用いて、信頼区間を求めます。
$$
(\bar{x}_1 - \bar{x}2) \pm t{\alpha/2}(\nu) \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}
$$

まとめ

母平均の差の信頼区間を求める3つのケースを解説しました。

ケース 母分散 使用する分布 主な特徴
Case 1 既知 標準正規分布 (Z分布) 理論の基礎
Case 2 未知だが等分散を仮定 t分布 プールされた分散 $s^2$ を使用
Case 3 未知で不等分散を仮定 t分布 (Welchの方法) 特殊な式で自由度を計算

どの手法を選択するかは、データが持つ前提条件によって決まります。信頼区間を正しく活用し、データに基づいた意思決定を行いましょう。

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?