以下の統計検定2級対策動画で用いられているスライドの一部です。
今回学ぶこと:t分布
統計学を学ぶ上で、正規分布の次に重要な確率分布が t分布 です。
- なぜt分布が必要なの?
- 標準正規分布と何が違うの?
この記事では、具体的な計算例を通して、t分布の基本的な考え方と使い方を明確に理解することを目指します。
学習の流れ
具体例から一般化へ、という流れで理解を深めます。
-
ステップ1:具体例からt分布を体感する
- ある製薬会社の錠剤データを使い、実際の計算を通して t分布 が必要になる場面を見ていきます。
-
ステップ2:一般化と定義のまとめ
- 具体例で得た知見をもとに、 t分布 の定義や性質を学術的に整理します。
ステップ1:具体例からt分布を体感する
【例題】 新しい錠剤の重量
ある製薬会社が開発した錠剤の重量は、正規分布に従うと仮定します。
無作為に 10個 抽出して重量(mg)を測定したデータがこちらです。
データ (n=10):
502, 496, 505, 499, 503, 498, 500, 495, 501, 501
【設問】
このデータを使って、以下の2つの値を計算してみましょう。
-
標本平均 $\bar{X}$
- 手元のデータ(標本)の平均値
-
不偏分散 $u^2$
- 母集団のばらつきを推定するための指標
解答1:標本平均 $\bar{X}$ の計算
まず、データの平均値を計算します。これが 標本平均 です。
$$
\begin{aligned}
\bar{X} &= \frac{502+496+...+501}{10} \
&= \frac{5000}{10} \
&= 500 \text{ (mg)}
\end{aligned}
$$
標本平均 $\bar{X}$ は 500mg と計算できました。
この値を使って、母集団の平均(母平均 $\mu$)を推測したいのですが…。
問題点:母分散 $\sigma^2$ がわからない
標本平均 $\bar{X}$ の信頼性を評価するには、通常、以下の 統計量 $Z$ を計算します。この $Z$ は 標準正規分布 に従います。
$$
Z = \frac{\bar{X} - \mu}{\sigma / \sqrt{n}}
$$
しかし、この式には 母標準偏差 $\sigma$ (母分散 $\sigma^2$ の平方根)が含まれています。
現実の分析では、母平均 $\mu$ と同じく 母分散 $\sigma^2$ も未知 の場合がほとんどです。
これでは $Z$ を計算できません。どうすればよいでしょうか?
解決策:母分散の「代役」を立てる
未知の母分散 $\sigma^2$ の代わりに、標本データから計算できる値で代用 します。
その代役こそが 不偏分散 $u^2$ です。
不偏分散は、母分散をより正確に推定するための指標です。
解答2:不偏分散 $u^2$ の計算 (1/2)
不偏分散は $u^2 = \frac{1}{n-1}\sum(X_i - \bar{X})^2$ で計算します。
まず、分子の 偏差平方和 $\sum(X_i - \bar{X})^2$ を求めます。
$$
\begin{aligned}
\sum(X_i - \bar{X})^2 = &(502-500)^2 + (496-500)^2 + \dots + (501-500)^2 \
= & (2)^2 + (-4)^2 + (5)^2 + \dots + (1)^2 \
= & 4 + 16 + 25 + 1 + 9 + 4 + 0 + 25 + 1 + 1 \
= & 86
\end{aligned}
$$
解答2:不偏分散 $u^2$ の計算 (2/2)
次に、計算した偏差平方和を 自由度 $n-1$ で割ります。
今回はデータが10個なので、自由度は $10-1=9$ です。
$$
u^2 = \frac{\sum(X_i - \bar{X})^2}{n-1} = \frac{86}{9} \approx 9.556
$$
これで 不偏分散 $u^2 \approx 9.556$ が計算できました。
新しい統計量「t」の登場
先ほどの統計量 $Z$ の未知の値 $\sigma$ を、いま計算した 不偏分散の平方根 $u$ で置き換えてみましょう。この新しい統計量を $t$ と呼びます。
$$
t = \frac{\bar{X} - \mu}{u / \sqrt{n}}
$$
この統計量 $t$ が従う確率分布こそが、 t分布 です。
今回の例では、この $t$ は 自由度9のt分布 に従います。
ステップ2:一般化と定義のまとめ
ここまでの具体例を踏まえ、t分布の定義や性質を整理していきましょう。
なぜt分布が必要なのか?
-
目的
- 母平均 $\mu$ を推測したい。
-
理想
- 母分散 $\sigma^2$ が既知なら、統計量 $Z$ が標準正規分布に従うことを利用できる。
-
現実
- 母分散 $\sigma^2$ は未知 の場合がほとんど。
-
解決策
- 母分散の代わりに 不偏分散 $u^2$ を使い、新しい統計量 $t$ を作る。
- この統計量 $t$ が従うのが t分布。
定義:不偏分散とt統計量
不偏分散 $u^2$
標本データから母分散を推定する値。分母が $n-1$ になるのが特徴。
$$
u^2 = \frac{1}{n-1}\sum_{i=1}^{n}(X_i - \bar{X})^2
$$
t統計量
母標準偏差 $\sigma$ の代わりに不偏標準偏差 $u$ を用いて標準化した値。
$$
t = \frac{\bar{X} - \mu}{u / \sqrt{n}}
$$
この $t$ は 自由度 $n-1$ のt分布に従います。
t分布の性質 (1) - 形状
t分布は、標準正規分布と似た性質を持っています。
- 平均が 0
- 左右対称 な釣鐘型の分布
t分布の性質 (2) - 裾の厚さ
標準正規分布との最も重要な違いは 裾の厚さ です。
- t分布は標準正規分布よりも 裾が厚い (fat tail) 。
- 理由: 母分散 $\sigma^2$ という固定値の代わりに、標本ごとに変動する推定量 $u^2$ を使うことによる 不確実性 が反映されているため。
- 結果として、0から遠い 極端な値が発生する確率が少し高く なります。
t分布の性質 (3) - 自由度との関係
t分布の形状は 自由度 (df) によって変化します。
- 自由度 ( $n-1$ ) が 大きく なるほど、t分布は 標準正規分布に近づく 。
- 理由: 標本サイズ $n$ が大きくなると、不偏分散 $u^2$ の推定精度が上がり、不確実性が減少するため。
- 目安として、自由度が 30 を超えると、ほぼ標準正規分布とみなせることがあります。
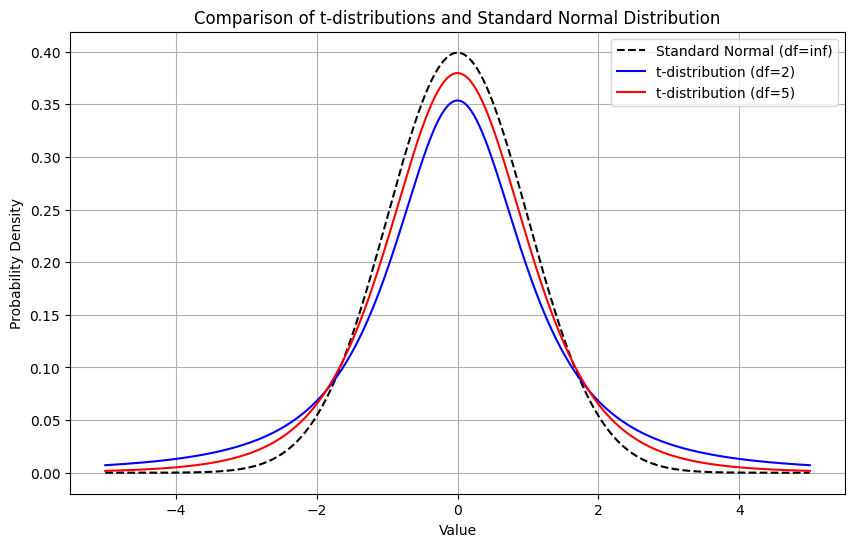
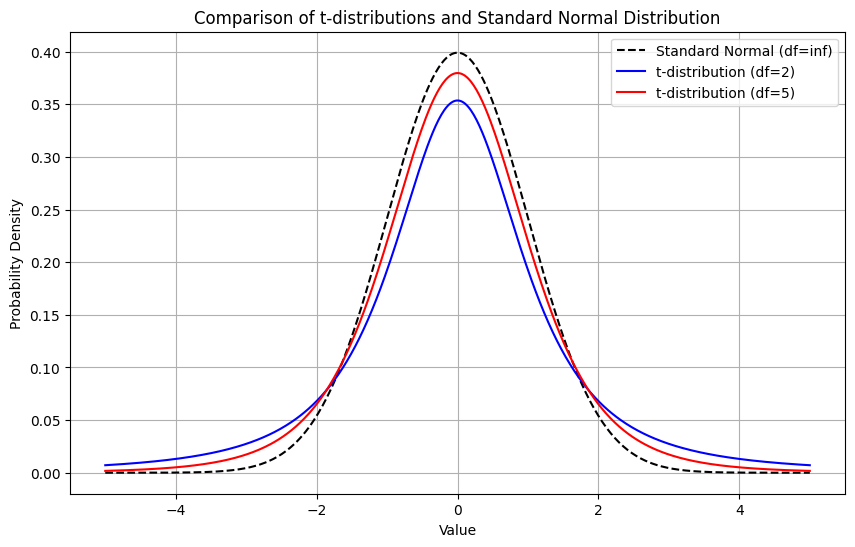
グラフによる形状の比較
自由度の違いによるt分布の形状の変化をグラフで確認しましょう。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t, norm
df1, df2 = 2, 5
x = np.linspace(-5, 5, 500)
pdf_t1, pdf_t2, pdf_norm = t.pdf(x, df=df1), t.pdf(x, df=df2), norm.pdf(x)
plt.figure(figsize=(10, 6))
plt.plot(x, pdf_norm, label='Standard Normal (df=inf)', color='black', linestyle='--')
plt.plot(x, pdf_t1, label=f't-distribution (df={df1})', color='blue')
plt.plot(x, pdf_t2, label=f't-distribution (df={df2})', color='red')
plt.title('Comparison of t-distributions and Standard Normal Distribution')
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()
まとめ (1/2)
-
t分布の必要性
- 母分散 $\sigma^2$ が未知 の場合に、標本平均 $\bar{X}$ の分布を評価するために用いる。
-
t統計量
- 母標準偏差の代わりに 不偏標準偏差 $u$ を使って計算する。
$$
t = \frac{\bar{X} - \mu}{u / \sqrt{n}}
$$
- 母標準偏差の代わりに 不偏標準偏差 $u$ を使って計算する。
まとめ (2/2)
-
自由度 (df)
- t分布の形状を決めるパラメータで、$n-1$ で計算される。
-
t分布の性質
- 標準正規分布と似た釣鐘型だが、裾がより厚い。
- 自由度が大きく なるにつれて 標準正規分布に近づく 。
t分布は、より実践的な統計手法である 区間推定 や 仮説検定 の根幹をなす、非常に重要な確率分布です。
この基本をしっかり押さえて、次のステップに進みましょう!