はじめに

エラトステネスの篩とは、$n$ 以下の自然数について素数判定表を生成するアルゴリズムです。
計算量 $O(n\log\log n)$ で¹予め表を生成してしまえば $1<k\le n$ の範囲の整数は定数時間で判定が行えるので、一定の範囲の整数について大量に素数判定を行う場合（素数の個数を数える、素因数分解を行うなど）は個々の数を素数判定するのに比べ非常に高速になります。

しかし、この $O(n\log\log n)$ という計算量は素数の逆数の総和が $O(\log\log n)$ に漸近していくという定理を用いているなど、かなり非直感的です。
本記事では計算量の実験的な確認を行うとともに他のアルゴリズムとの比較を行いました。²

手法

エラトステネスの篩のPythonによる実装

エラトステネスの篩の基本的なアルゴリズムは擬似コードで以下のように書けます。

2 から n までの数に対し素数か否かを表すbool配列を用意し、Trueで初期化する
2 から n まで小さい順に、その数 p が素数であればそれ以降の p の倍数をFalseにする

これをPython 3 で実装すると

def eratosthenes(n):
    is_prime = [False, False] + [True] * (n-1)
    for p in range(2, n+1):
        if not(is_prime[p]):
            continue
        for k in range(p*2, n+1, p):
            is_prime[k] = False
    return is_prime

のようになります。

また、

下から順に確認しているため、「$p$ の倍数」のうち $(p-1)$ 倍以下はすでに消されているので $p^2$ から確認し始めればよい
$\sqrt{n}$ 以上の素数 $p$ については上と同じく倍数はすでに消されているためもう確認する必要はない
2 以外の偶数は素数でないことがわかっているため予め False にして飛ばしてしまって良い

などの条件を利用すれば無駄な計算を減らし高速化することができます（計算量のオーダーは変わらない）。
これのPythonでの実装は以下のようになります。

def eratosthenes2(n):
    is_prime = ([False, True] * (n//2+1))[0: n+1]
    is_prime[1] = False
    is_prime[2] = True
    for i in range(3, n+1, 2):
        if not(is_prime[i]):
            continue
        if i*i > n:
            break
        for k in range(i*i, n+1, i):
            is_prime[k] = False
    return is_prime

以降との比較のため素数の数を返す関数とします。

def num_prime_e1(n):
    return eratosthenes(n).count(True)
def num_prime_e2(n):
    return eratosthenes2(n).count(True)

計算量の悪い「エラトステネスの篩」

上ではbool配列によるフラグで素数判定を行っていましたが、もっと素朴に数列そのものから「合成数を消す」という操作をしようと思うとこのような実装になるかもしれません³。

def quasi_eratosthenes(n):
    nums = [i for i in range(2, n+1)]
    primes = []
    while nums:
        p = nums.pop(0)
        primes.append(p)
        if p * p > n:
            break
        i = 0
        while i < len(nums):
            if nums[i] % p == 0:
                nums.pop(i)
                continue
            i += 1
    return primes + nums

def num_primes_qe(n):
    return len(quasi_eratosthenes(n))

この場合、リストから最後尾以外でpopを行っていることや素数に対して余分な計算を行っているため計算量は悪化し、$O(n^2)$ 程度になると考えられます。
これについては本当は遅い「似非エラトステネスの篩」の罠｜Zenn において詳しく解説されています。

試し割り法との比較

個々の整数を逐一素数判定する方法と比較します。

最も単純には整数 $k$ が素数か判定するには $k$ 未満の数すべてで割り算を試して割り切れないかを確かめればよいです。

def num_prime_1(n):
    r = 0
    for k in range(2, n+1):
        for l in range(2, k):
            if k % l == 0:
                break
        else:
            r += 1
    return r

計算量は $O(n^2)$ となります。

流石に無駄が多すぎるのでもう少し頭を使うと、$\sqrt{k}$ 以下の数で割り切れなければそれ以上の数で割り切れることはないので $\sqrt{k}$ で打ち止めにすることができます。

def num_prime_2(n):
    r = 0
    for k in range(2, n+1):
        flag = True
        for l in range(2, k):
            if l * l > k:
                break
            if k % l == 0:
                flag = False
                break
        if flag:
            r += 1
    return r

これだと計算量は $O(n^{3/2})$ になります。

また、SymPyには素数判定を行う関数sympy.isprimeがあります。これを用いると

from sympy import isprime
def num_primes_sympy(n):
    r = 0
    for k in range(2, n+1):
        if isprime(k):
            r += 1
    return r

のように簡単に書けます。ミラー-ラビン素数判定法を使用しているらしい⁴です。
公式に実装されているだけあって高速です。

さらに、割り算を実行するのを素数だけにすると整数全部試すよりかなり回数が減ります。
出現した素数を配列に格納するようにすると以下のようになります。

def num_prime_3(n):
    primes = []
    for k in range(2, n+1):
        flag = True
        for p in primes:
            if p * p > k:
                break
            if k % p == 0:
                flag = False
                break
        if flag:
            primes.append(k)
    return len(primes)

ベンチマーク方法

ベンチマークにはJupyter notebook(IPython)のマジックコマンドである%timeitを使用しました。
あとに続くステートメントの実行時間を自動で計測することができ、複数試行による不確かさの評価や実行時間が短い場合にループさせてくれるなど簡単に実行時間の計測を行うことができます。

%timeit num_prime_e1(100)
# => 13.5 µs ± 345 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

for i in [20 * 2**i for i in range(10)]:
    print(i, end=" ")
    %timeit num_prime_e1(i)

のように $n$ を変化させながら実行時間の推移を計測しました。

実行環境は以下の通りです。
Windows 10 Home 20H2
Intel(R) Core(TM) i7-8700 CPU @ 3.20GHz 3.19 GHz
実装RAM 16.0 GB
Python 3.6.4 :: Anaconda, Inc.
Jupyter notebook vesion 5.4.0

結果と考察

実行時間の推移

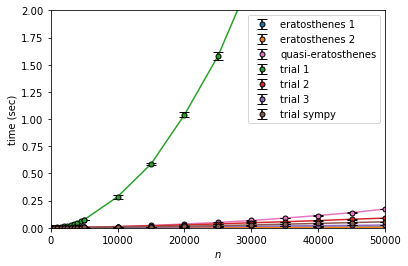
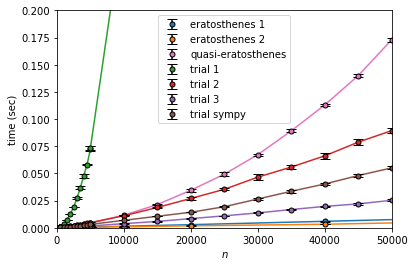
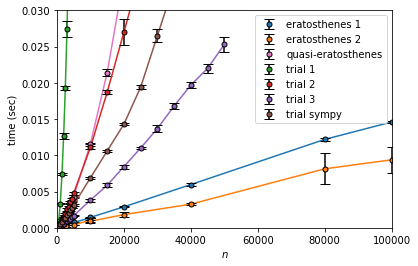
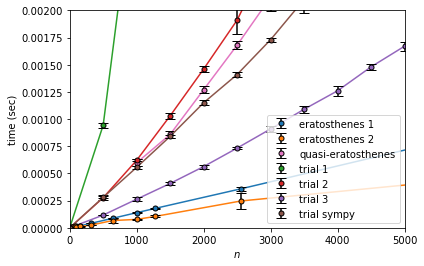
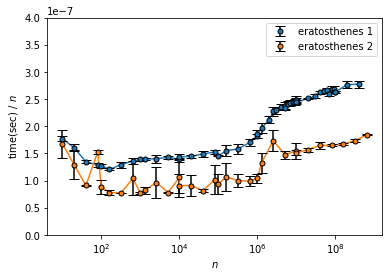
計測した $n$ に対する実行時間の推移を以下に示します。
凡例はそれぞれ
eratosthenes 1 : 単純なエラトステネスの篩
eratosthenes 2 : 計算量の改善を行ったエラトステネスの篩
quasi-eratosthenes : 計算量の悪い「エラトステネスの篩」
trial 1 : 試し割り法、すべての整数の割り算を行ったもの
trial 2 : 試し割り法、$\sqrt{k}$までの整数で割り算を行ったもの
trial 3 : 試し割り法、$\sqrt{k}$までの素数で割り算を行ったもの
trial sympy : 試し割り法、sympy.isprimeで判定を行ったもの
です。

trial 1 が非常に遅く、次にquasi-eratosthenesが遅いです。これらは下に凸に上昇（加速度的な増加というやつ）しており、 $n^2$ っぽい振る舞いになっています。
また計算量を改善した試し割り法と比較しても大きな差をつけて（高速な方の）エラトステネスの篩は高速であることがわかります。

計算量の評価

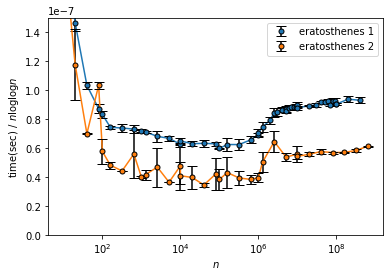
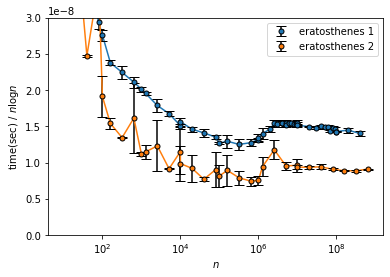
エラトステネスの篩の計算時間を理論的な計算量 $O(n\log\log n)$ や$n$、$n\log n$と比較します。

eratosthenes 2 はブレが大きいですが、どちらも（$n\sim 10^6$ を除き） $\text{time}$ が $n$ に対しては増加、$n \log n$ に対しては減少していっているのがわかります。よってこれらの計算量は $O(n)$ と $O(n\log n)$ の中間程度であると推定できます。
$\text{time}/(n \log\log n)$ は $n$ が大きいところでは増加しているっぽいですが中間くらいでは緩やかに減少している風なので丁度いいくらいでしょう。（$n$ が小さいところで発散している感じなのはオーバーヘッドで定数時間取られてしまっているのが割り算で大きくなってしまったと考えられます。）
すなわち、エラトステネスの篩の計算量が $O(n\log\log n)$ ということに矛盾しない結果が得られました。

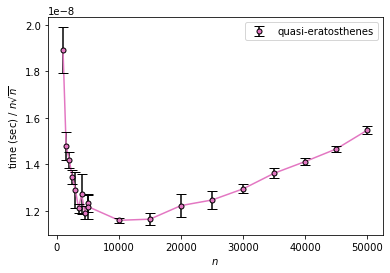
一方、quasi-eratosthenes を見ると、

$n^2$ に対してだいたい収束しており、少なくとも $n^{3/2}$ よりは大きいことがわかります。

試し割り法の計算量

試し割り法の場合の計算時間も比較してみます。

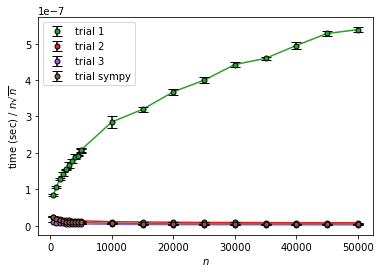
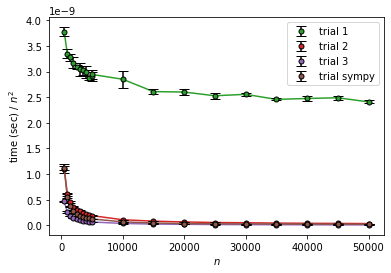
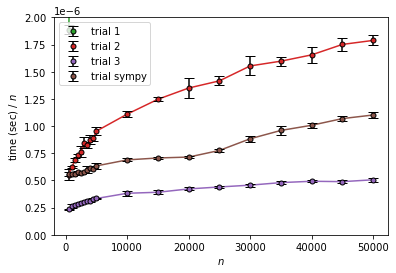
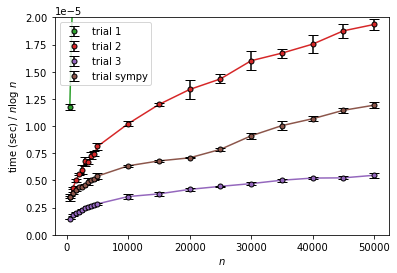
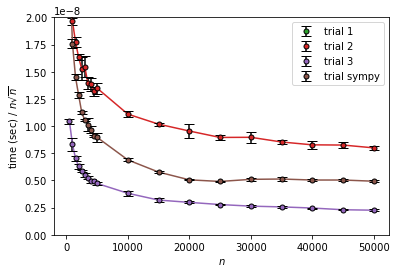
trial 1 は $n^{3/2}$ に対しては明らかに増加、 $n^2$ に対してはほぼ水平という感じで $O(n^2)$ らしくなっています。

trial 2、trial 3、trial sympy は $n$ や $n\log n$に対しては増加、$n^{3/2}$ に対してはそこそこ収束していそうです。
減少しているようにも見えますが、$n$ が小さい場合にはエラトステネスのときと同様にオーバーヘッドの影響があるというのと、
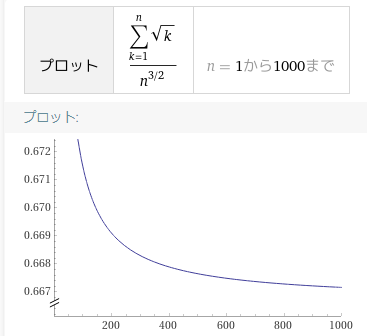
$\sum_{k=1}^n \sqrt{k}$ は $n\to \infty$ では $\frac{2}{3}n^{3/2}$ に漸近するものの、序盤は結構差があるのでこれの影響で収束しきっていないんじゃないかと考えられます。

まとめ

以上でエラトステネスの篩と他の素数判定アルゴリズムとの比較、計算量の評価を行い、エラトステネスの篩の速さを確認することができました。
エラトステネスの篩では $O(N\log\log N)$，試し割りと「似非エラトステネスの篩」では $O(N\sqrt{N})$～$O(N^2)$ と，漸近的な計算量と矛盾しない結果が得られました．
まともに実装できていたようで良かったです。

$n\sim 10^6$ で時間が増大しているのは何故なんでしょう？このあたりで多倍長整数がメモリを確保し直すとかなんでしょうか。

なお、今回はクエリが非常に多いという場合で比較を行いましたが、1度だけ大きな整数の素数判定を行うというような場合はもちろん1個の素数判定を行ったほうが速いです⁵。アルゴリズムは時と場合に応じて適切に使いましょう。

計算量の導出についてエラトステネスのふるいとその計算量｜高校数学の美しい物語 ↩
ついでにいうとTwitterで話題のエラトステネスがちゃんとエラトステネスになっていないコード解説記事をみて自分がちゃんと実装できるのかどうか不安になったということがあります。 ↩
Wikipediaに記載されている「具体例」が非常に紛らわしい書き方をしているのでこれを見て実装するとこうなる可能性があるかもしれないですね。 ↩
https://docs.sympy.org/latest/modules/ntheory.html#sympy.ntheory.primetest.isprime ↩
おそらくsympy.isprime関数を使うのが一番速いでしょう。ライブラリが提供されているなら車輪の再発明をするよりたいてい速いです。 ↩

エラトステネスの篩の計算量を実験で確認する