本記事は「日本語プログラミング言語「プロデル」 Advent Calendar 2021」24日目の記事です.
18日目の記事 で実装した乱数サンプリングアルゴリズムの実践として,水素原子波動関数の確率密度を計算することで電子雲の散布図を生成してみます.
水素原子の電子雲
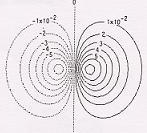
「水素の原子軌道」というと,このような図↓がよく示されます1.
研究と教育と追憶と展望 露本伊佐男のブログ 「オービタル(原子軌道)を図示するときによくある混乱、間違い」 http://tsuyu.cocolog-nifty.com/blog/2008/05/post_4e04.html より
この図は電子がその位置にある確率が一定以上の空間を塗りつぶしたもの(等値面プロット)ですが,この方法だと入れ子になっている構造などを観察することができません.
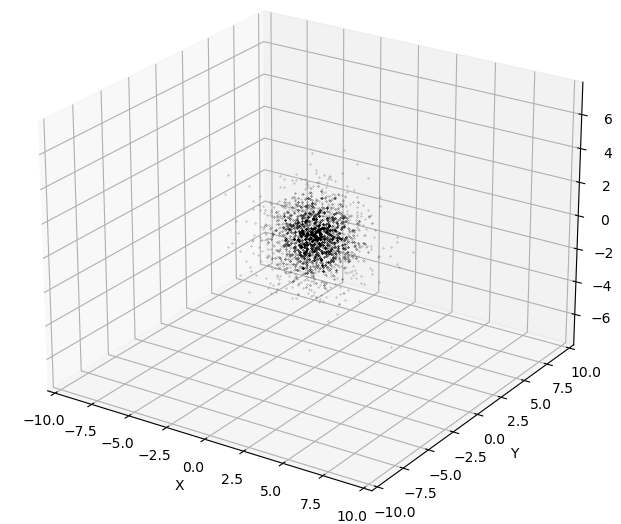
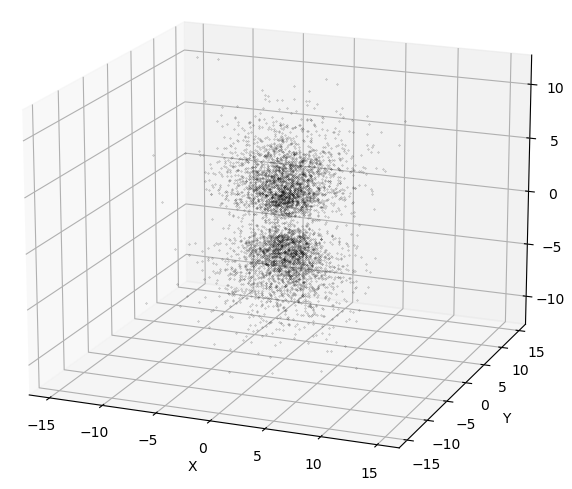
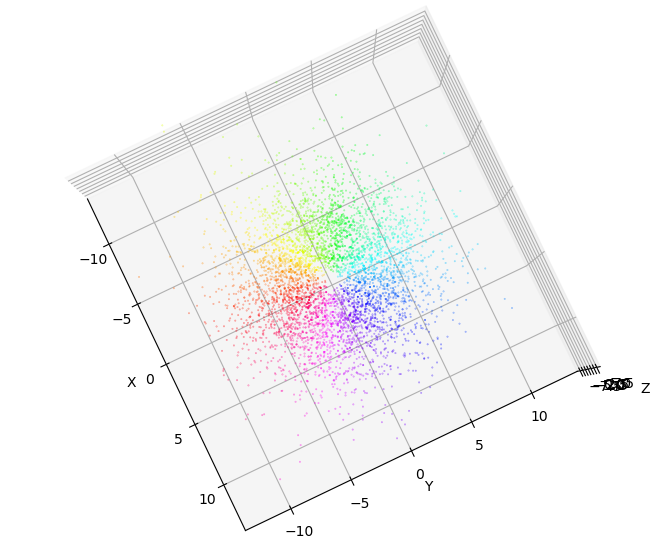
一方,確率密度に比例した密度で散布図を描くと以下のようになります.
太刀川達也 et al.「ガラス内彫刻による電子雲の可視化」平成20年度埼玉大学総合研究機構研究プロジェクト(研究経費)研究成果報告書 より
より直感的で軌道の内部構造もよく観察できますね.
本記事ではこの「確率密度に比例した密度で座標点を取る」という計算を乱数サンプリングアルゴリズム(特にMCMC)を用いて行います.
水素原子波動関数の解
水素原子のような中心に1つだけ正電荷があって,その周りに1つだけ電子がいるとき,電子の波動関数は
\left[-\frac{\hbar^2}{2\mu}\nabla^2+V({x})\right]\Psi(x)=E\Psi(x)\\
V(r)=-\frac{Ze^2}{4\pi\varepsilon_0 r}
のようになります.$-e$は電子の電荷,$Ze$は原子核の電荷で,$\mu$は中心電荷に対する電子の相対運動を考えた時の換算質量で,原子殻は電子より1836×質量数倍重いのでほぼ電子質量と一致します.
この方程式は解が多数出てくるので整数 $n,;l,;m$ でインデックス付けして,解が
\Psi(r, \theta, \phi)=N_{l,n}
\left(\frac{\rho}{n}\right)^l e^{-\frac{\rho}{n}} L_{n+l}^{2l+1}\left(\frac{\rho}{n}\right)
\times M_{l,m} P_l^{|m|}(\cos\theta)e^{im\phi}\\
\ \\
\rho=\frac{Z}{a_0}r,\; a_0=\frac{4\pi\varepsilon_0\hbar^2}{\mu e^2},\\
N_{l,n}=-\sqrt{\frac{4(n-l-1)!}{n^4[(n+l)!]^3}}\left(\frac{Z}{a_0}\right)^{\frac32},\;
M_{l,m}=(-1)^{\frac{m+|m|}{2}}\sqrt{\frac{2l+1}{4\pi}\frac{(l-|m|)!}{(l+|m|)!}}\\
L_k^j(x): \text{ラゲールの陪多項式}, P_k^j(x):\text{ルジャンドルの陪多項式}
と表せます.$n=1,2,\dots,; 0\leq l < n,; -l\leq m \leq l$ です.
導出は こちら などを参照のこと.
ややこしいので文字をまとめて書くと
\Psi(r, \theta, \phi)=A_{l,m,n}\times R_{n,l}(\rho)\times Y_{l,m}(\theta,\phi)
のように極座標の動径 $r$ を規格化した $\rho$ の関数 $R_{n,l}$ と方位 $\theta, \phi$ の関数 $Y_{l,m}$ の関数の積で表せるということがわかります.
これらの関数の具体的な形を自力で求めるのはなかなか大変なのですが,なんとWikipediaに解が載っています. 水素原子におけるシュレーディンガー方程式の解 - Wikipedia
また,Wolfram Alpha など特殊関数を計算できるライブラリを用いればここに載っていないものも求めることが可能ですが,ラゲールの陪多項式を求める際はここでの式と表記が変わるので注意が必要です(ラゲールの陪多項式とassociated Laguerre polynomialsの指しているものが違った件).
係数を無視して関数形をリストアップすると $\newcommand\mathabs[1]{|#1|}$
| $n$ | $l$ | $R_{n,l}(x)$ |
|---|---|---|
| 1 | 0 | $-1$ |
| 2 | 0 | $x-2$ |
| 2 | 1 | $-1$ |
| 3 | 0 | $-\frac{x^2}{2}+3x-3$ |
| 3 | 1 | $x-4$ |
| 3 | 2 | $-1$ |
| $\vdots$ | $\vdots$ | $\vdots$ |
| $l$ | $ \mathabs{m} $ | $Y_{l,m}(\cos\theta)e^{im\phi}$ |
|---|---|---|
| 0 | 0 | $1$ |
| 1 | 0 | $\cos\theta$ |
| 1 | 1 | $-\sin\theta \times [\cos\phi / \sin\phi]$ 2 |
| 2 | 0 | $(3\cos^2\theta-1)$ |
| 2 | 1 | $-\cos\theta\sin\theta \times [\cos\phi / \sin\phi]$ 2 |
| 2 | 2 | $-(\cos^2\theta-1) \times [\cos2\phi / \sin2\phi]$ |
| $\vdots$ | $\vdots$ | $\vdots$ |
と書けます.
なお,$m=\pm k$ のときの $\phi$ 成分は $\cos k\phi \pm i\sin k\phi$ という複素数表示になりますが,波動関数同士の線形結合は同じく波動関数になることを利用して $\cos k\phi ,; \sin k\phi$ と実数関数になるように分解しています.
比例定数 $A_{n,l,m}$ についてはまだ手つかずですが,後述するようにMCMCでは確率密度関数の比例定数は結果に関わらないので,計算の手間を省くためむしろ積極的に放置します.
これで波動関数 $\Psi$ の具体的な関数形を求めることができました.
電子の存在確率は $|\Psi|^2$ と表すことができるので波動関数を求めて2乗するだけで電子の確率分布を求めることができます.
たとえば $l=2, m=0, n=1$ (2pz軌道)のときは
\Psi_{\text{2p}_z}=\dfrac{1}{4\sqrt{2\pi}}\left(\frac{Z}{a_0}\right)^{3/2}\rho\;\exp\left(-\frac{\rho}{2}\right)\cos\theta
なので
|\Psi_{\text{2p}_z}|^2\propto \rho^2\;\exp\left(-\rho\right)\cos^2\theta
です.
MCMCによる座標計算
ここで得られた確率密度に従う座標点を乱数サンプリングアルゴリズムを用いて計算します.
確率密度関数は多項式とexpが絡んだ複雑な式なので逆関数法は難しく,また高エネルギーな軌道ほど広い領域に渡って広がっていくので棄却法を使うと棄却率がかなり高くなり計算に非常に時間がかかります.
そこで,MCMCを採用します.MCMCだと規格化定数を計算する必要がないため先頭の定数項をすべて無視できるというのも嬉しいポイントです.
MCMCによる水素原子電子雲の計算は既に先行研究があります3
- 日曜化学(2.5):メトロポリス・ヘイスティングス法を用いた電子雲の可視化(Python/matplotlib)
- https://twitter.com/dc1394/status/1414534075440799748
が,プロデルでも実装してみます.
(2022/02/09 動径関数の計算が間違っていたのを修正しました)
「C:\Git\Misc\random_package_produire\乱数.rdr」を参照する
【主量子数:整数】=1
【方位量子数:整数】=0
【磁気量子数:整数】=0
【サンプル数:整数】=10000
【提案幅X:浮動小数】=5.0
【提案幅Y:浮動小数】=5.0
【提案幅Z:浮動小数】=5.0
【初期値X:浮動小数】=1.0
【初期値Y:浮動小数】=1.0
【初期値Z:浮動小数】=1.0
もし(プログラムの起動時設定)が無なら
「ファイルが指定されていません」を出力する
そうでなければ
【引数長さ】=プログラムの起動時設定の個数
もし引数長さ≧3ならば
主量子数=プログラムの起動時設定(1)
方位量子数=プログラムの起動時設定(2)
磁気量子数=プログラムの起動時設定(3)
もし終わり
もし引数長さ≧4なら サンプル数=プログラムの起動時設定(4)
もし引数長さ≧7ならば
提案幅X=プログラムの起動時設定(5)
提案幅Y=プログラムの起動時設定(6)
提案幅Z=プログラムの起動時設定(7)
もし終わり
もし引数長さ≧10ならば
初期値X=プログラムの起動時設定(8)
初期値Y=プログラムの起動時設定(9)
初期値Z=プログラムの起動時設定(10)
もし終わり
もし終わり
サンプル数個の目的の乱数列
【サンプル数N】個の,目的の乱数列を求める手順
【前のX】=初期値X
【前のY】=初期値Y
【前のZ】=初期値Z
【前のL】={X=前のX,Y=前のY,Z=前のZ}での対数尤度関数
サンプル数N回,『
【次のX】=前のX+((-提案幅X)から(提案幅X)までの一様乱数)
【次のY】=前のY+((-提案幅Y)から(提案幅Y)までの一様乱数)
【次のZ】=前のZ+((-提案幅Z)から(提案幅Z)までの一様乱数)
【次のL】={X=次のX,Y=次のY,Z=次のZ}での対数尤度関数
――「hoge[次のL]」を出力して改行
もし(次のL>前のL)または(0から1までの一様乱数<(次のL-前のL)の自然対数乗)ならば
前のX=次のX
前のY=次のY
前のZ=次のZ
前のL=次のL
もし終わり
「[前のX],[前のY],[前のZ]」を出力して改行
』を繰り返す
終わり
[座標]での,対数尤度関数を求める手順
X=座標から「X」を得たもの
Y=座標から「Y」を得たもの
Z=座標から「Z」を得たもの
ρ=(X^2+Y^2+Z^2)の平方根
θ=acos(Z÷ρ)
φ=atan(Y÷X)
もしX<0ならπをφへ足す
ーー「[ρ],[θ],[φ]」を出力して改行
ρでの二乗対数動径関数+((θとφでの球面調和関数)^2)の自然対数を返す
終わり
[ρ]での,二乗対数動径関数を求める手順
【ρn】=ρ÷主量子数
主量子数について分岐
1の場合
-ρn×2を返す
2の場合
方位量子数について分岐
0の場合
(-ρn×2+((2-ρn)^2)の自然対数)を返す
1の場合
(-ρn×2+(ρn^2)の自然対数)を返す
分岐終わり
3の場合
方位量子数について分岐
0の場合
(-ρn×2+((6-6×ρn+ρn^2)^2)の自然対数)を返す
1の場合
(-ρn×2+(((4-ρn)×ρn)^2)の自然対数)を返す
2の場合
(-ρn×2+(ρn^4)の自然対数)を返す
分岐終わり
4の場合
方位量子数について分岐
0の場合
(-ρn×2+((24-36×ρn+12×ρn^2-ρn^3)^2)の自然対数)を返す
1の場合
(-ρn×2+(((20-10×ρn+ρn^2)×ρn)^2)の自然対数)を返す
2の場合
(-ρn×2+(((6-ρn)×ρn^2)^2)の自然対数)を返す
3の場合
(-ρn×2+(ρn^6)の自然対数)を返す
分岐終わり
5の場合
方位量子数について分岐
1の場合
(-ρn×2+(((120-90×ρn+18×ρn^2-ρn^3)×ρn)^2)の自然対数)を返す
分岐終わり
分岐終わり
終わり
[θ]と,[φ]での,球面調和関数を求める手順
方位量子数について分岐
0の場合
1を返す
1の場合
磁気量子数について分岐
0の場合
cos(θ)を返す
1の場合
sin(θ)×cos(φ)を返す
(-1)の場合
sin(θ)×sin(φ)を返す
分岐終わり
2の場合
磁気量子数について分岐
0の場合
(3×(cos(θ))^2-1)を返す
1の場合
sin(θ)×cos(θ)×cos(φ)を返す
(-1)の場合
sin(θ)×cos(θ)×sin(φ)を返す
2の場合
(sin(θ))^2×cos(2×φ)を返す
(-2)の場合
(sin(θ))^2×sin(2×φ)を返す
分岐終わり
3の場合
磁気量子数について分岐
0の場合
(5×(cos(θ))^3-3×cos(θ))を返す
1の場合
(5×(cos(θ))^2-1)×cos(φ)を返す
(-1)の場合
(5×(cos(θ))^2-1)×sin(φ)を返す
2の場合
cos(θ)×(sin(θ))^2×cos(2×φ)を返す
(-2)の場合
cos(θ)×(sin(θ))^2×sin(2×φ)を返す
3の場合
(sin(θ))^3×cos(3×φ)を返す
(-3)の場合
(sin(θ))^3×sin(3×φ)を返す
分岐終わり
分岐終わり
終わり
尤度は対数を取って計算しています.特に複雑な計算になると多数の確率の積を取ることでアンダーフローを起こしやすいためです.
コンソールで引数を与えて波動関数の種類,サンプル数,提案分布の幅,初期値を変えられるよう処理をしています.
"C:\Program Files (x86)\Produire\pconsole.exe" C:\home\rdr\水素原子.rdr 2 1 0 50000 10 10 10> hydro2p0.csv
のようにすることで,計算結果を書き出します.
可視化
前節で座標がCSV形式で書き出せるようになったので,これをプロットして可視化してみます.
ただし,プロデル上で3D散布図を描けるようにするには時間が足りなかったのでプロットにはPythonを用いています.
(2020/02/09 ※注意 上記修正後結果が合わなくなったので修正中です.今後結果が変わる可能性があります.)

$4\mathrm{d}_{x(5z^2-r^2)}$ 軌道
etc...
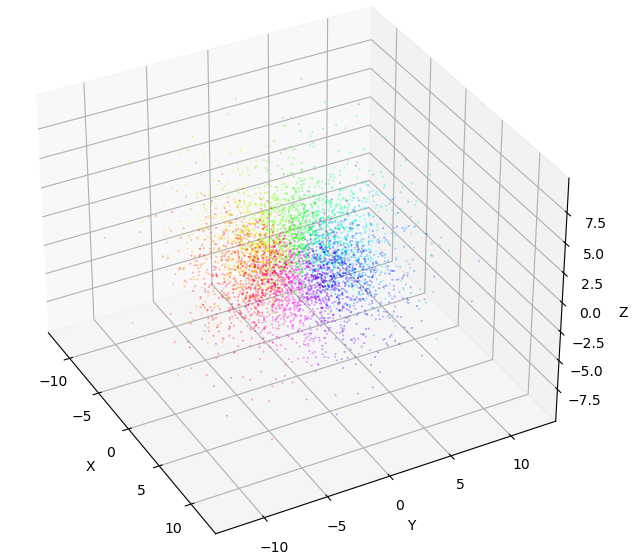
また,波動関数の符号も書き出し,符号に応じて着色するようにすれば位相に応じて色を変えることもできます.
こちらのほうが波動関数の節が観察しやすいですね.
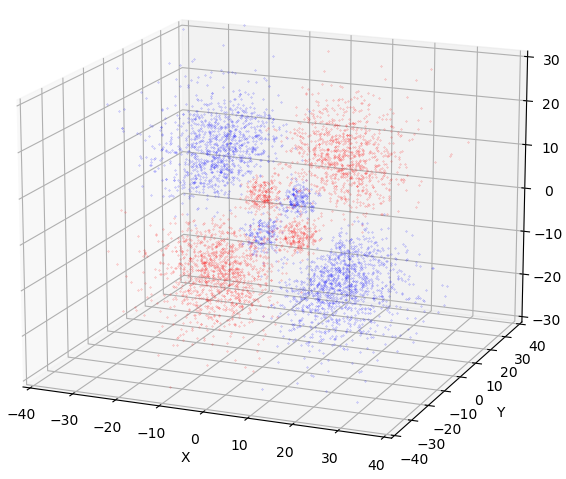
$4\mathrm{d}_{x(5z^2-r^2)}$ 軌道 位相着色版
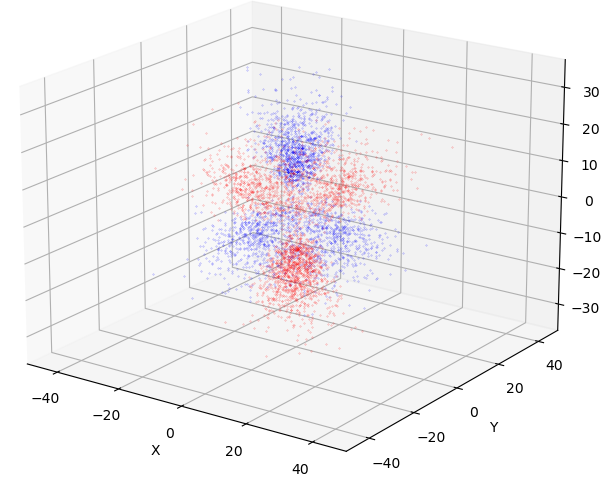
$4\mathrm{f}_{z(5z^2-3r^2)}$ 軌道 位相着色版
また,波動関数の実数化を行わずに位相で色をつけるとこんなケバいドーナツ4みたいな形になります.
これの$\pm$が合わさってダンベル形になるというのがすこし不思議ですね.
発展
ここまで確率分布のサンプリングにはMCMCが最適かのような言い方をしてきましたが,実は今回の水素原子オービタルのような確率0の面で複数の領域に分断されている確率分布のサンプリングはMCMCはサンプリングに失敗することがあります.
現在位置から確率に応じて移動していくアルゴリズムなので,移動幅が小さすぎると谷を渡れず1つのドメインから抜け出せなくなったりします5.
水素原子オービタルの場合はだいたいの形状が定性的にわかるので結果を見ながら適宜調整すればよいのですが,ベイズ推定に使うときなどはそもそも分布の形を知りたいので分布形状をカンニングすることはできません.
未知の分布にMCMCを適用する場合は,初期値を様々に変えながら分布を適切にサンプリングできているか統計的な検証が必要となります.
MCMCの問題点を解消するために,Metropolis-Hastings法を改良した様々な手法が開発されています(Hybrid Monte Carlo法:分子動力学法の手法を導入することでより自己相関の少ないサンプリングができる,Replica Exchange法:温度パラメータを導入し多数のサンプル列間でで交換しながらサンプリングすることで局所的なドメインから抜け出しやすくする,etc...).
実装が大変なのでここではやりませんが……
あとがき
ソースだけ読んでもそれなりにアルゴリズムがわかりやすかったのではないでしょうか.
日本語プログラミング言語ならではですね.
可視化ツールや位相付き版を含めソースは GitHub で公開しています.
電子雲をぐるぐる動かしながら観察するのは楽しいのでぜひやってみてください.