導入
ラゲールの陪多項式とは,常微分方程式
\left(x\frac{d^2}{dx^2}+(k+1-x)\frac{d}{dx}+(n-k)\right)L_n^k(x)=0 \tag{1}
を満たす多項式 $L_n^k(x)$ のことです.
水素原子のシュレディンガー方程式を解くと動径方向の関数として現れることで有名です.
\Psi(r, \theta, \phi)=N_{l,n}
\left(\frac{\rho}{n}\right)^l e^{-\frac{\rho}{n}} L_{n+l}^{2l+1}\left(\frac{\rho}{n}\right)
\times M_{l,m} P_l^{|m|}(\cos\theta)e^{im\phi}\\
\ \\
\rho=\frac{Z}{a_0}r,\; a_0=\frac{4\pi\varepsilon_0\hbar^2}{\mu e^2},\\
N_{l,n}=-\sqrt{\frac{4(n-l-1)!}{n^4[(n+l)!]^3}}\left(\frac{Z}{a_0}\right)^{\frac32},\;
M_{l,m}=(-1)^{\frac{m+|m|}{2}}\sqrt{\frac{2l+1}{4\pi}\frac{(l-|m|)!}{(l+|m|)!}}\\
L_k^j(x): \text{ラゲールの陪多項式}, P_k^j(x):\text{ルジャンドルの陪多項式}
(もっぱら水素原子波動関数を描画したいときなど)プログラムでこの多項式を扱いたいことがままあります.
同時に現れるルジャンドル陪多項式は英語で"associated Legendre polynomials"であり,特殊関数を扱える多くのライブラリでassoc_legendreなどの名前で実装されています.
同様にして,ラゲール陪多項式は英語ではもちろん"associated Laguerre polynomials"といい,assoc_laguerreという名前の関数は「ラゲール陪関数 (associated Legendre functions) を計算する。」と書いてあるのですが,これを使って上記の波動関数を計算すると結果が合いません.
例えば水素原子の $2p_{\text{z}}$ 軌道は量子数 $n=2,l=1,m=0$ で,動径関数は $\displaystyle N\frac{\rho}{2}\exp(-\frac{\rho}{2})$ で,ラゲール陪多項式は定数式であるはずです.これを $L_3^3(x)$ で得ようと Wolfram alpha で計算しようとすると……
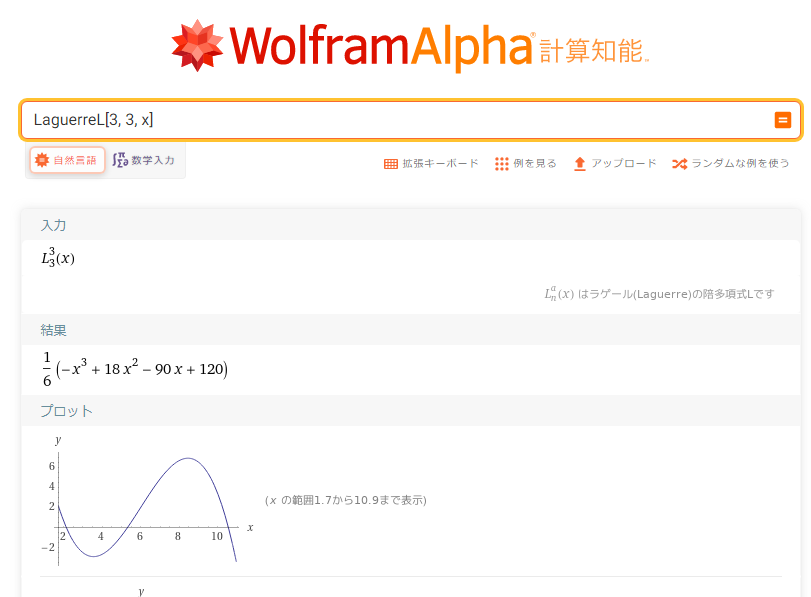
https://www.wolframalpha.com/input?i=LaguerreL%5B3%2C+3%2C+x%5D&lang=ja
3次関数が現れます.
このような関数だと$2p_{\text{z}}$ 軌道は動径方向に節を持つことになってしまいます.
明らかにおかしいですね.
じつは,得たい関数 "$L_3^3$" は(Wolfram Alphaのクエリでは) LaguerreL[0, 3, x] のように,指数(0,3)と入力することで得られます.
この"バグ"はどのようにして現れるのでしょうか?
定義
実は,日本語での「ラゲール陪多項式」と英語の「associated Laguerre polynomials」は定義が異なります.
日本語では前述したとおり
\left(x\frac{d^2}{dx^2}+(k+1-x)\frac{d}{dx}+(n-k)\right)y(x)=0 \tag{1}
です1が,英語では
\left(x\frac{d^2}{dx^2}+(k+1-x)\frac{d}{dx}+n\right)y(x)=0 \tag{2}
になっています2.
最後の項が違いますね.この少しの差で結果がかなり変わってしまいます.
associated は「関連する」という意味なので決まった拡張の仕方があるわけではないというのが原因でしょう.実際のところ,英語版は「generalized Laguerre polynomials (associated Laguerre polynomials とも呼ばれる)」という感じなので,ルジャンドル多項式-ルジャンドル陪多項式の関連との整合性などはあまり意識されていないのかもしれません.
が,流石にそれぞれバラバラでは困ります.どう関連しているのでしょうか?
関係式
Wikipediaでの記号をよく見ると,日本語版のラゲール陪多項式は $L_n^k(x)$,英語版では $L_n^{(k)}(x)$と肩の指数のカッコの有無が異なっている事がわかります.これで区別することにしましょう3.
さて,$k=0$の場合は日英どちらの定義でも微分方程式は
\left(x\frac{d^2}{dx^2}+(1-x)\frac{d}{dx}+n\right)y(x)=0
なので $L_n^0$ と $L_n^{(0)}$は(定数倍を除いて)一致します4.
これは特にラゲール多項式と呼ばれ,
L_n(x)=e^x\frac{d^n}{dx^n}(x^ne^{-x})
と表せることなどが知られています5.
これを使って,日本語版は
L_n^k(x)=\frac{d^k}{dx^k}L_n(x)
英語版は
L_n^{(k)}(x)=(-1)^k\frac{d^k}{dx^k}L_{n+k}(x)
となります(※後述).
左辺が一致するように式変形すれば,
L_n^{(k)}(x) = (-1)^kL_{n+k}^k(x)\\
L_n^k(x)=(-1)^k L_{n-k}^{(k)}(x)
が得られます.
つまり,(英語版で実装されている多くのライブラリで)日本語版のラゲール多項式を計算したければ LaguerreL[n - k, k, x] のようにすればよいわけですね.
$L_{n+l}^{2l+1}(\rho)$ は $L_{n-l-1}^{(2l+1)}(\rho)$ となります.
ざっと見た限り,日本語文献で水素原子波動関数を解く教材ではみんな日本語版,英語文献では英語版の式が使われているようです.
これだけ違う式がはっきり分断されているのにあまり有名な話ではないようです.不思議ですね.
ラゲール多項式との関係式の導出
ついでですが,途中で出てきた(※)の式を導出を計算しておきます.
ラゲール陪多項式は常微分方程式(1)の解なので,
$$
xy''+(k+1-x)y'+(n-k)y=0 ;\Leftrightarrow; y=AL_n^k(x)
$$
($A$ は定数)です.(この他に解がないかどうかなどの議論は省略します.)
両辺を $x$ で微分すると
xy'''+y''+(k+1-x)y''-y'+(n-k)y'=0\\
x(y')''+((k+1)+1-x)(y')'-(n-(k+1))y'=0
となり,これは指数が $n,k+1$ のときの $y'$ の常微分方程式(1)なので $y'=L_n^{k+1}(x)$ となります.
すなわち
L_n^{k+1}(x)=A\frac{d}{dx} L_n^{k}(x)
です.この漸化式を繰り返し適用すると帰納的に
L_n^{k}(x)=A'\frac{d}{dx} L_n^{k-1}(x)=A''\frac{d^2}{dx^2} L_n^{k-2}(x)\\
=\dots=A'''\frac{d^k}{dx^k} L_n^{0}(x)
となり,関係式が得られます.定数は何でも良いので=1とします.
($A', A''$ のプライムは単に別の定数の意味で微分ではありません.)
英語版でも同様に,
xy''+(k+1-x)y'+ny=0 \;\Leftrightarrow\; y=AL_n^{(k)}(x)\\
xy'''+y''+(k+1-x)y''-y'+ny'=0\\
x(y')''+((k+1)+1-x)(y')'-(n-1)y'=0\\
y'=L_{n-1}^{(k+1)}(x)
L_{n-1}^{(k+1)}(x)=A\frac{d}{dx} L_n^{k}(x)
L_n^{k}(x)=A'\frac{d}{dx} L_{n+1}^{(k-1)}(x)=A''\frac{d^2}{dx^2} L_{n+2}^{(k-2)}(x)\\
=\dots=A'''\frac{d^k}{dx^k} L_{n+k}^{(0)}(x)
となります.
こちらでは漸化式の係数をすべて-1として係数が $(-1)^k$ となるようにしているようです.
おそらく同じ $n$ の $L_n^{(k)}$ の最大次の係数が一致するようにしているのだと思います.
(2022/02/27)
なお,今回の内容は EMANの物理学 さんの解説記事 ラゲールの微分方程式 に周辺情報や導出なども含めより詳しく解説されています.
まあ,筆者の興味に沿った流れでのまとめということで.