スピノーダル線を描く
はじめに
混合溶液は、モル分率$x$と温度$T$の値によっては安定に存在できず、相分離を起こします。
その$x-T$相図には、安定領域と不安定領域を分ける線、スピノーダル線があります。
本稿では、
自由エネルギー関数$F$を用いた安定性解析により、
スピノーダル線を作成する方法を述べます。
例として、
等温2成分系を想定し、
自由エネルギーの安定性の判別方法を述べた後、
化学ポテンシャルを、Margulesの活量係数モデルで与え、
そのギブズエネルギーを用いて解析します。
溶液の安定性解析
自由エネルギーの最小化原理を前提とします。
ある極値での平衡状態で2成分溶液が安定であるための条件は、
自由エネルギー関数$F$が極値の周りの微小なズレに対して増加することです。
$F$は成分1,2の物質量$n_1,n_2$の関数$F(n_1,n_2)$であるとします。
物質量の微小変化$n_1\to n_1+\delta n_1$と$n_2\to n_2+\delta n_2$に対して、
$F$を、極値$F_\mathrm{0}$の周りで、
$$
F = F_\mathrm{0}+\delta F+\frac{\delta^2 F}{2}
$$
と展開します。
極値周りなので、1次の変分$\delta F$は0と考えてよいです。
2次の変分$\delta ^2F$は
$$
\delta ^2 F = [\delta n_1,\delta n_2]^T H(F)(n_1,n_2) [\delta n_1,\delta n_2]
$$
と書けます。
ここで、$H(F)$は$F$のHesse行列であり、
$H(F)(n_1,n_2)$は次のように定義された2x2の対称行列です。
H(F)(n_1,n_2)=
\begin{bmatrix}
\frac{\partial^2F_{}}{\partial n_1^2} & \frac{\partial F_{}}{\partial n_1\partial n_2} \\
\frac{\partial F_{}}{\partial n_2 \partial n_1} & \frac{\partial ^2 F_{}}{\partial n_2^2}
\end{bmatrix}
極値周りで系が安定な条件は、
$\delta^2 F$が任意のベクトル$[\delta n_1,\delta n_2]$に対して常に正であることです。
つまり、$H(F)(n_1,n_2)$が正定値行列であるとき、系は安定です。
以上の議論は多成分系でも同様に成立します。
対称なポテンシャルの2成分系
前節で導いた安定性の判定条件を用いて$x-T$相図を書いてみましょう。
成分1と2の化学ポテンシャルを、Margulesのモデルに基づいて、
\mu_1 = \mu_1^\circ(T) + RT\ln x + \xi (1-x)^2
\mu_2 = \mu_2^\circ(T) + RT\ln (1-x) + \xi x^2
と書きます。
ここで、
$x$は成分1のモル分率、
$\xi$は相互作用パラメータ、
$\mu_1^\circ(T)$と$\mu_2^\circ(T)$は標準化学ポテンシャルです。
自由エネルギー関数の安定性を調べます。
均一な相状態を仮定すると、そのギブズエネルギー関数$G(n_1,n_2)$は
G(n_1,n_2)=n_1\mu_1+n_2\mu_2
と書けます。
関数$G(n_1,n_2)$に対して、そのHesse行列が正定値となるかどうかを調べ、安定性を判別します。
結果を示します。
簡単のため、$R=1$、$\mu_1^\circ(T)=\mu_2^\circ(T)=0$としました。
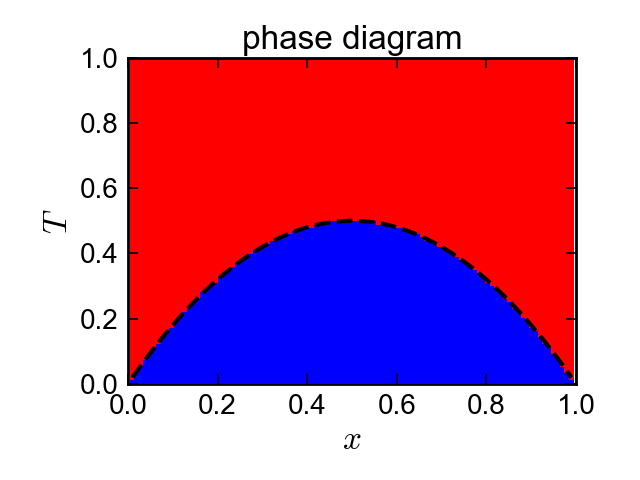
図の破線は別途解析的に求めたスピノーダル線です。
図の赤で塗られた領域は1相領域、青で塗られた領域は2相領域です。
実装はPythonで行いました。
自動微分を備えたライブラリを使うことで、解析的にHessianを求める労力を削減できます。
今回はJaxを用いました。
数値誤差があるので、positive definiteの判定のところで、$\mathrm{det}$に対して条件を少し緩めています。
from jax import hessian,grad
import jax.numpy as np
import numpy as onp
import matplotlib.pyplot as plt
jax.config.update("jax_enable_x64", True)
N = 101 # plot points N^2
xi = 1.0 # interaction parameter
eps = 1e-12 # for numerical error of stability analysis
x_a = np.linspace(0.01,0.99,N) # molar fraction list
T_a = np.linspace(0.01,xi,N) # temperature list
xx,TT = onp.meshgrid(x_a,T_a) # search grid
stability = onp.empty((N,N)) # stability result
def mu(x1,x2,T): # Margules model
mu_std = 0.0
return mu_std + T*np.log(x1) + xi*x2**2
def G(n,T): # Gibbs energy as function of n1, n2
n1,n2 = n
x1 = n1/(n1+n2)
x2 = 1.0-x1
return n1*mu(x1,x2,T) + n2*mu(x2,x1,T)
def Gm(x,T): # Gibbs energy as function of x
x1 = 1.0*x
x2 = 1.0-x
return x1*mu(x1,x2,T) + x2*mu(x2,x1,T)
# stability analysis
for i in range(N):
for j in range(N):
x = xx[i,j]
T = TT[i,j]
#
h = hessian(lambda n: G(n,T))(np.array([x,1.0-x]))
stability[i,j] = ( np.trace(h) > 0.0 ) and ( np.linalg.det(h) > -eps )
# もちろん1変数関数としてもできる。
# ddGm = grad(grad(lambda x: Gm(x,T)))(x)
# stability[i,j] = ddGm > 0.0
plt.pcolor(xx,TT,stability,cmap="bwr")
plt.plot(x_a,2.0*xi*x_a*(1.0-x_a),"k--")
plt.xlim(0.0,1.0)
plt.ylim(0.0,1.0)
plt.xlabel(r"$x$")
plt.ylabel(r"$T$")
plt.title(r"phase diagram")
plt.savefig("phase-separation-diagram.pdf")
plt.show()
非対称なポテンシャルの2成分系
\mu_1 = \mu_1^\circ(T) + RT\ln x + \{\xi_{12}+2(\xi_{21}-\xi_{12})x\} (1-x)^2
\mu_2 = \mu_2^\circ(T) + RT\ln (1-x) + \{\xi_{21}+2(\xi_{12}-\xi_{21})(1-x)\} x^2
$\xi_{12}=\xi_{21}$の時、前節の式に還元されます。
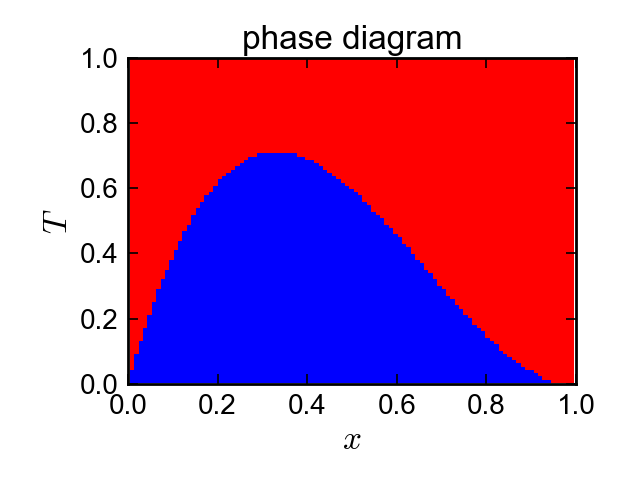
Ethanol-Water系についての相互作用パラメータを採用します。
結果として、前節の結果とは異なり、対称な形ではないスピノーダル線が描かれることがわかります。
from jax import hessian,grad
import jax.numpy as np
import numpy as onp
import matplotlib.pyplot as plt
jax.config.update("jax_enable_x64", True)
N = 101 # plot points N^2
# Perry, Robert H.; Green, Don W. (1997). Perry's Chemical Engineers' Handbook (7th ed.). New York: McGraw-Hill. pp. 13:20. ISBN 978-0-07-115982-1.
xi12, xi21 = 1.6022, 0.7947 # Ethanol(1)-Water(2)
eps = 1e-12 # for numerical error of stability analysis
x_a = np.linspace(0.01,0.99,N) # molar fraction list
T_a = np.linspace(0.01,xi,N) # temperature list
xx,TT = onp.meshgrid(x_a,T_a) # search grid
stability = onp.empty((N,N)) # stability result
def mu1(x1,x2,T): # Margules model
mu_std = 0.0
return mu_std + T*np.log(x1) + (xi12+2*(xi21-xi12)*x1)*x2**2
def mu2(x1,x2,T): # Margules model
mu_std = 0.0
return mu_std + T*np.log(x2) + (xi21+2*(xi12-xi21)*x2)*x1**2
def G(n,T): # Gibbs energy as function of n1, n2
n1,n2 = n
x1 = n1/(n1+n2)
x2 = 1.0-x1
return n1*mu1(x1,x2,T) + n2*mu2(x1,x2,T)
def Gm(x,T): # Gibbs energy as function of x
x1 = 1.0*x
x2 = 1.0-x
return x1*mu1(x1,x2,T) + x2*mu2(x1,x2,T)
# stability analysis
for i in range(N):
for j in range(N):
x = xx[i,j]
T = TT[i,j]
#
h = hessian(lambda n: G(n,T))(np.array([x,1.0-x]))
stability[i,j] = ( np.trace(h) > 0.0 ) and ( np.linalg.det(h) > -eps )
# もちろん1変数関数としてもできる。
# ddGm = grad(grad(lambda x: Gm(x,T)))(x)
# stability[i,j] = ddGm > 0.0
plt.pcolor(xx,TT,stability,cmap="bwr")
# plt.plot(x_a,2.0*xi*x_a*(1.0-x_a))
plt.xlim(0.0,1.0)
plt.ylim(0.0,1.0)
plt.xlabel(r"$x$")
plt.ylabel(r"$T$")
plt.title(r"phase diagram")
plt.savefig("phase-separation-diagram2.pdf")
plt.show()
おわりに
ややマニアックな話ですが、任意の活量係数モデルに対し、
自動微分で相図がささっと作成できる嬉しさを感じてくださることを期待しています。
本当は共存曲線の話もしようかと思ったのですが、
とりあえず2024年駆け込みで投稿します。よいお年を!